Метод оценки параметров радиоканалов сети LTE

Функционирование мобильных сетей сотовой связи третьего поколения к настоящему времени стало реальностью. Стандарты третьего поколения позволили обеспечить предоставление пользовательских услуг (потоковое вещание, передача мультимедийной информации, высокоскоростной интернет и др.), недоступных в традиционных сетях второго поколения [1, 2].

Дальнейшим развитием мировых телекоммуникационных технологий в области мобильной связи является разработка и внедрение стандартов четвертого поколения (4G), обеспечивающих еще большие скорости передачи данных и повышение качества предлагаемых пользовательских услуг при общем снижении затрат в эксплуатации. Одной из технологий, призванных для решения насущных задач современных телекоммуникаций, является технология Long Term Evolution, (LTE). Соответственно этому, сети мобильной связи, реализованные на основе такой технологии, называют LTE-сети. Для успешной, эффективной работы этих сетей применяют соответствующие методы сетевого и системного управления, которые требуют постоянного и надежного метрологического обеспечения и получения соответствующих эффективных оценок параметров измеряемых случайных величин, процессов или полей [3, 4]. Для получения оценок измеряемых параметров могут использоваться: выборочные методы оптимальной оценки случайных величин, рекурсивные методы оценки случайных величин или рекурсивные методы оценки случайных процессов [5].

Для предоставления доступа и распределения ресурсов между абонентскими станциями (АС) в сети LTE каждые 0,5 мс производятся измерения характеристик канала и каждые 40 мс отправляются отчеты о средних значениях измеренных параметров [6]. Эти выборочные оценки статистических параметров могут далее использоваться для задач управления и принятия решений по распределению частотного ресурса между АС [7–9]. Однако для автоматических систем управления выборочные оценки не очень удобны из-за того, что для ее получения необходимо затратить определенный интервал времени. Более конструктивным типом оценок являются рекурсивные процедуры оценивания, которые дают текущую оценку процессу в реальном времени. Кроме того, считается, что параметры каналов сети являются статистически независимыми. И, следовательно, оценивание параметров можно производить независимо для каждого канала. Поэтому актуальной научной задачей является исследование статистической связи между радиоканалами сети LTE, а также разработка методов оценки измеряемых параметров.

1. Измеряемые параметры радиоканалов и их статистические характеристики

Проведены измерения отношения сигнал / помеха + шум (ОСПШ)

h = 10 •

lg

f p

c

л

p +PV n n ' ш /

дБ

в частотном диапазоне 1920–1980 МГц на смежных частотах 1 920 000 и 1 920 015 кГц. Эксперимент состоял в следующем. Генерировались тестовые сигналы на частотах 1 920 000 кГц (канал 1) и 1 920 015 кГц (канал 2). На приемной стороне производились измерения ОСПШ в каждом канале. Для набора статистики было произведено N =1000 измерений на протяжении 428,6 мс через интервал времени A t =0,4286 мс.

По полученным реализациям рассчитаны:

– средние значения:

1N m =—^h(k), k = 1,2,..., N - дискретное время,

N k =1

для процесса 1 среднее значение ОСПШ m1 = 11,0671, для процесса 2 среднее значение ОСПШ m2 = 10,9773;

– дисперсии (разброс относительно средних значений):

1 N            2

о = — £(h(k) - m) , для процесса 1 дисперсия о2 = 33,2875, для процесса 2 дисперсия о2 = 27,0391;

- автокорреляционные функции R ( т ) , ( т - временной сдвиг):

N —т

R ( т ) = —— ^ h ( k ) h ( к + т ) — m ² .

Нормированные корреляционные функции представлены на рис. 1.

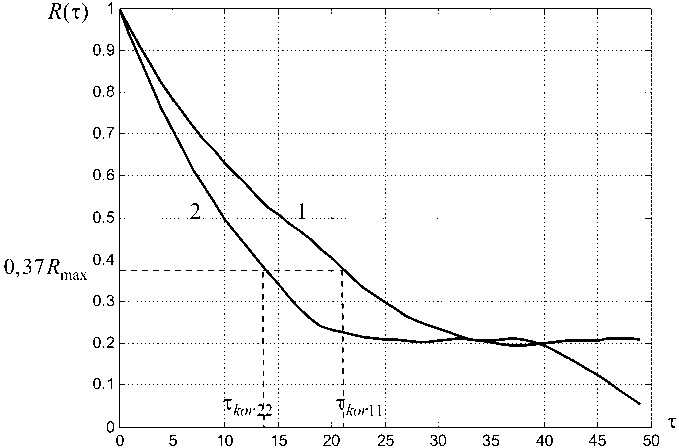
Рис. 1. Графики нормированных корреляционных функций процессов 1 и 2

Из данных графиков видно, что максимальные значения R _max данные функции имеют при т = 0 и медленно убывают при увеличении временного сдвига. Судя по данным графикам, можно сделать вывод о том, что они имеют экспоненциальный вид. В соответствии с теоремой Дж. Дуба можно утверждать, что полученные процессы являются марковскими.

Числовой характеристикой, служащей для оценки «скорости изменения» реализаций случайного процесса, является интервал корреляции тkor , определяемый выражением да

' k = R (0) f ^{R (} d ^{Т .}

Полученные функции корреляции можно аппроксимировать выражением

R (т) = e-“'т, где а = 1/т kor.

Очевидно, что при т = т _kor экспонента e ^-1 = 0,37 . Считается, что интервал корреляции т _kor определяется в точке, где корреляционная функция R ( т ) = 0,37 R m ax .

Для определения скорости изменения процессов по полученным графикам корреляционных функций определены интервалы корреляции. Для процесса 1 интервал корреляции составляет т kor 11 = 21 отсчет, что соответствует временному интервалу т _kor 11 At = 21 - 0,4286 = 9,0006 мс. Для процесса 2 интервал корреляции составляет т kor ₂₂ = 13 отсчетов, что соответствует временному интервалу т _kor 11 -A t = 13 - 0,4286 = 5,5718 мс.

Для определения статистической зависимости двух процессов построена взаимная корреляционная функция. На рис. 2 представлен график нормированной корреляционной функции двух процессов.

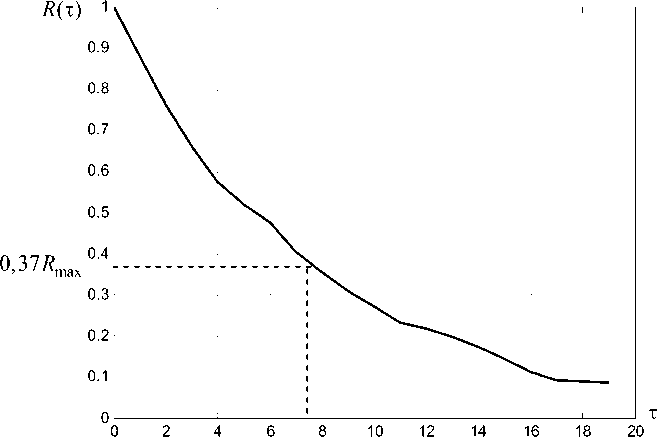
^ког\2 ^ког2\

Рис. 2. График нормированной взаимной корреляционной функции

По данному графику определен интервал взаимной корреляции между двумя процессами. Интервал корреляции составляет т _kor = 7,5 отсчетов. Следовательно, во времени он составляет т ko_r At = 7,5 - 0,4286 = 3,2145 мс. Таким образом, можно утверждать, что процессы в смежных каналах являются статистически зависимыми.

Для оценки параметров канала необходимо представление процессов (состояние каналов) в виде математической модели.

• 2.    Математические модели марковских процессов

—

Дискретный векторный марковский процесс x (k) можно представить в форме уравнений состояния: —                        —                  — x (k +1) = F - x (k) + G-Ц k),                                                               (1)

— где x (k) – вектор состояния; F , G матрицы (для одномерного случая коэффициенты) состояния

— и возбуждения соответственно; ^ (к) - порождающее векторное белое гауссовское поле с нуле- вым средним.

Коэффициенты F f ij = exp { -a j A t } имеют физический смысл величин, обратных интервалу корреляции т _ког процесса x ( к ) , а у = 1/ т _koгi j , A t = к - ( к - 1 ) - шаг. Коэффициенты G g ij = Уо ² f ij ( 1 - f ij ) определяют масштаб случайных изменений процесса x ( к ) , о ² - спектральная плотность мощности порождающего процесса £ ( к ) .

Система уравнений (1) может распасться на n -независимых одномерных систем, когда коэффициенты fij и gij , играющие роль связей между i и j уравнениями, а следовательно и процес- сами, приобретают значения fij =0 и gij =0 при i * j . Уровень этих связей может изменяться под действием управляющих воздействий.

Представим двумерную модель состояния каналов:

• —    (к +1) = F•к (к) + G - —(к),

  
  

где h – ОСПШ в канале.

Матрица состояния F представляется в виде:

F f exP (-a11A t ) exP (-a12A t ))

^ exp (-a 21A t) exp (-a22A t )J, где ап =-----, а12 =-----, а21 =-----, а22 =-----, At - шаг.

^т ког 11           ^т ког 12           ^т ког 21            ^т ког 22

Матрица возбуждения G представляется в виде:

G Г У^ f .1 (1 - f .1 ) У о ² f .2 (1 - f 12 ) '

Цо2 f21(1 - f21) У О2 f22(1 - f22) , , где fj = exP(-ajAt).

Модель (2) дополняется уравнениями наблюдения. Модель наблюдения задается системой линейных алгебраических соотношений:

• —     —  — —

• 3.    Метод оценки измеряемых параметров радиоканалов

y ( к ) = H J h ( к ) + m 1+ n ( к ),                                                                (5)

— где H – матрица, которая задает ослабление измеряемых процессов; шум наблюдения n (k)

является векторным белым гауссовский шумом с дисперсией a n и нулевым средним, m - вектор средних значений.

Для оценки случайных процессов Калманом и Бьюси разработана достаточно эффективная оптимальная в гауссовом и линейном приближениях процедура, получившая название «фильтра Калмана – Бьюси». В основе этой процедуры лежит математическая модель в виде уравнения со-ˆ стояния, и уравнения наблюдения. Сама же процедура оценки h (к) имеет следующий вид:

-                —

h (к) = F • h (к -1) + K(к)[у (к) - H • F • h (к -1)], где K (к) - коэффициент, обеспечивающий устойчивость и оптимальную скорость сходимости алгоритма к установившемуся состоянию. Данный коэффициент в фильтре Калмана– Бьюси подлежит рекурсивному вычислению на каждом шаге согласно алгоритму:

K ( к + 1) = P ( к ) HN n ¹. (7)

Вычисление апостериорной дисперсии:

P(k +1) = FV(k)FT + GN^(k)GT .(8)

Уравнение для априорной дисперсии:

V(k +1) = [I - K (k)H ]P(k +1),(9)

где N^, Nn - соответственно значения спектральных плотностей мощности порождающего шума ————

^ ( k ) и шума наблюдения n ( k ) .

На рис. 3 представлена структурная схема алгоритма оценки (6).

Рис. 3. Структурная схема дискретного алгоритма оценки фильтра Калмана – Бьюси

Здесь уместно отметить, что чем более коррелированными являются отсчеты наблюдаемого

—— процесса h (k), h (k -1), ^ тем выше качество получаемой оценки.

Характерно, что в выражение для апостериорной дисперсии P ( k ) не входят значения ни h ( k ) , ни y ( k ) , то есть P ( k ) зависит лишь от времени и параметров самого фильтра и параметров, а не значений наблюдаемого процесса.

• 4.    Анализ метода оценки измеряемых параметров радиоканалов

  • 4.1.    Анализ метода оценки мгновенных значений измеряемых параметров

при статистически независимых частотных каналах

Задача анализа предполагает наличие модели наблюдения, модели процедуры оценки и модели процедуры обработки результатов анализа.

Структурная схема машинного эксперимента, включающего в себя модель наблюдения, модель оценки и модель обработки, представлена на рис. 4. ˆ

Чтобы убедиться, что получаемые оценки h ( k ) адекватно отображаются в результате рекурсивных процедур, получим метод анализа выборочного массива, в котором соответствующие статистики сравниваются с расчетными. Для этого в результате сравнения полученной оценки

Г                                    —7,4

ОСПШ h ( k ) и сформированного процесса h ( k ) получаем выборочные апостериорные значения

_г                                                                — дисперсии ошибки оценки P(k). На основе оценок h (k) выборочных значений сигнала h (k),

— Г — формируется массив ошибок оценки err(k) = h (k) - h (k), которая используется для получения выборочной апостериорной дисперсии ошибки оценки P =

N -1

N

^ err ( k ) 2 .

k = 1

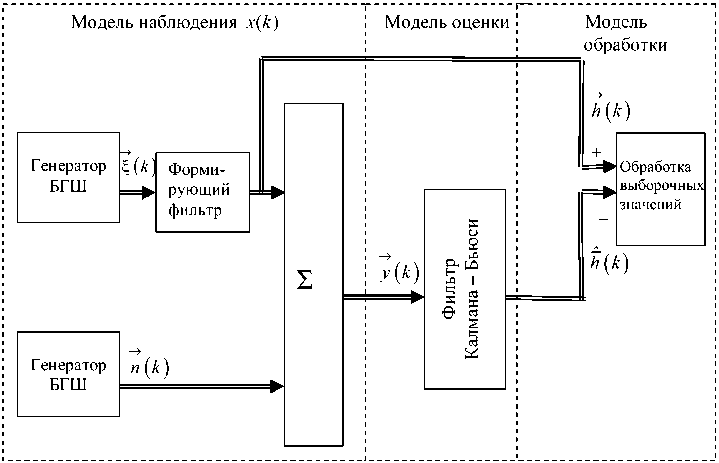
Рис. 4. Структурная схема машинного эксперимента

В связи с тем, что наблюдения производятся на фоне шумов наблюдения проведен анализ качества оценок в зависимости от отношения мощности измеряемого процесса P _пр к мощности шумов наблюдения P _ш :

q = 10 • ig ( P npf Р ш ) .

Анализ качества получаемых оценок ОСПШ проведен с помощью относительной апостериорной дисперсии ошибки оценки P P _пр в условиях установившегося режима фильтра, когда k ^ ^ , а относительная апостериорная дисперсия ошибки оценки становится постоянной.

Построены зависимости относительной апостериорной дисперсии ошибки оценки от q в канале наблюдения при значениях интервала корреляции т _kop = 1, что характерно для быстрых изменений канала и т _kop = 20, что характерно для медленных изменений канала. На рис. 5 представлены данные зависимости. Нижняя кривая соответствует апостериорной дисперсии при интервале корреляции т _kop = 20, а верхняя кривая - при т _kop = 1.

Рис. 5. Зависимость относительной апостериорной дисперсии ошибки оценки от q

Из полученных графиков видно, что значения относительной апостериорной дисперсии ошибки оценки больше при меньшем значении интервала корреляции (при быстрых изменениях канала). Так же из полученных графиков можно сделать вывод о том, что при малых значениях q =0 дБ относительная апостериорная дисперсии ошибки оценки является достаточно большой и составляет 0,3 для быстрых изменений параметров канала и 0,217 для медленных изменений. При увеличении q относительная апостериорная дисперсии ошибки оценки вначале резко снижается, затем снижение замедляется, и при достижении q = 10 дБ практически относительная апостериорная дисперсии ошибки оценки не изменяется.

• 4.2.    Сравнительный анализ метода оценки измеряемых параметров

при статистически зависимых частотных каналах

Как было показано выше, частотные каналы сети LTE являются статистически зависимыми. Одномерные представления модели состояния и решения по нахождению оценки и соответствующего управления – это решения присущи одному элементу системы. Системных свойств, таких как целостность, эмерджентность, при данных решениях не проявляется. Отметим, что система приобретает присущие ей сверхинтегральные свойства целостности и эмерджентности за счет взаимодействия составляющих ее элементов. Поэтому возникает необходимость проанализировать имеющие место механизмы взаимосвязей между отдельными элементами многомерной системы, за счет которых и создается сама система и ее системные интегральные свойства.

В используемом нами методе анализа переменных состояния имеется два механизма учета указанных взаимосвязей: через недиагональные элементы матриц F и G в уравнениях состояния (2) и через недиагональные элементы матрицы наблюдение H в уравнении (5).

Частым случаем многомерной системы есть взаимонезависимые уравнения, при условии f j = 0 и g ij = 0, i Ф j . Однако такое предположение на практике редко выполняется. Более того, система с взаимно независимыми состояниями переменных теряет системные свойства, перестает быть системой. Действительно, в LTE сети изменение параметров каналов приводит к необходимости перераспределения сетевых ресурсов. С другой стороны: если необходимо отобразить больше тех или иных системных свойств, то следует задействовать больше взаимных связей f_ij и g_ij , и тем сложнее оказывается модель самой системы.

Очевидно, пренебрежение взаимными связями приводит к потере качества оценок, а соответственно и управления, ибо этим самым игнорируются наиболее важные системные свойства целостности и эмерджентности.

Проведен сравнительный анализ методов оценки измеряемых параметров при статистически зависимых частотных каналах. На рис. 6. представлены зависимости относительной апостериорной дисперсии ошибки оценки от интервала взаимной корреляции для двух каналов.

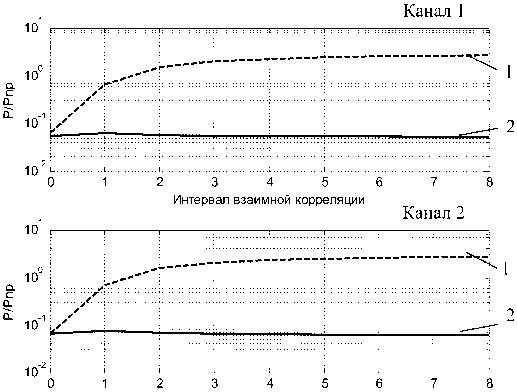
Интервал взаимной корреляции

Рис. 6. Зависимости относительной апостериорной дисперсии ошибки оценки от интервала взаимной корреляции

Кривые 1 на рис. 6, как для канала 1, так и для канала 2 соответствует значениям относительной апостериорной дисперсии ошибки оценки при независимом оценивании, т.е. считается, что диагональные элементы матриц F и G равны нулю (fij = 0, gij = 0 при i * j). Кривые 2 на рис. 6, как для канала 1, так и для канала 2 соответствуют значениям относительной апостериорной дисперсии ошибки оценки с учетом зависимости при оценивании, то есть считается, что диа- тональные элементы матриц F и G равны fy = exp

v  Tkorij у

, g y = V ° ² f j (1 - f j ) при i * j .

Из данных графиков видно, что при интервале взаимной корреляции равном нулю T j = 0 значения апостериорной дисперсии ошибки оценки, как при независимом оценивании, так и при учете зависимости совпадают. Это объясняется тем, что как при независимом оценивании, так и при учете статистической зависимости матрицы F и G имеют диагональный вид, и процессы между собой не коррелированны. При увеличении интервала взаимной корреляции T j = 1, значения апостериорной дисперсии ошибки оценки при независимом оценивании на порядок возрастают. С дальнейшим увеличением интервала взаимной корреляции T j = 2...4 апостериорная дисперсия ошибки оценки при независимом оценивании увеличивается приблизительно в разы. И с дальнейшим увеличением интервала взаимной корреляции ту = 5...8 рост апостериорной дисперсии ошибки оценки прекращается. Кроме того из данных графиков видно, что значения относительной апостериорной дисперсии ошибки оценки с учетом зависимости при оценивании остаются неизменными с увеличением интервала взаимной корреляции. Это говорит о том, что учет взаимных связей дает значительный выигрыш при оценивании статистически зависимых процессов. И выигрыш этот составляет больше, чем в 10 раз.

Выводы

• 1.    Проведены измерения ОСПШ в частотном диапазоне 1920…1980 МГц на смежных частотах 1 920 000 кГц (канал 1) и 1 920 015 кГц (канал 2). Анализ полученных реализаций показал, что процессы в смежных каналах являются статистически зависимыми.

• 2.    Предложено для оценки ОСПШ каналов использовать процедуру Калмана – Бьюси. Разработана структурная схема машинного эксперимента, которая состоит из модели наблюдения, модели процедуры оценки и модели процедуры обработки результатов анализа.

• 3.    Проведен сравнительный анализ методов оценки измеряемых параметров при статистически зависимых частотных каналах. Анализ показал, что учет взаимных связей дает значительный выигрыш (больше, чем в 10 раз) при оценивании статистически зависимых процессов.