Метод оценки параметров спектральных пиков

Оценка параметров сигналов, содержащих информацию о качественном и количественном составе анализируемых веществ, было и остается важной задачей в обработке данных приборов многокомпонентного анализа в аналитической химии, биологии и медицине. При этом требования к качеству обнаружения и особенно оценке параметров сигналов в присутствии шума, базовой линии и в условиях неполного разделения пиков постоянно растут, т. к. они определяют степень достоверности решений, принимаемых по результатам анализа. В частности, в приборах генетического анализа при расшифровке последовательности нуклеотидов необходимо определить кроме традиционных параметров — время выхода и амплитуда пиков — также ширину, площадь и признак полного или частичного разделения пиков. Все эти параметры нужны для оценки показателей качества расшифровки последовательности нуклеотидов в цепочке по методике Phred [1] .

Традиционные методы анализа данных аналитических приборов, как правило, включают предварительную обработку с целью минимизировать влияние на качество оценки информативных параметров сигнала случайного и детерминированного шумов, выбросов, базовой линии и эффекта неполного разделения пиков. В работе [2] рассматривается несколько программных пакетов предварительной обработки, применяемых, в частности, в исследованиях метаболомики на основе хроматографии и масс-спектрометрии.

Пакет XCMS [3], выполняет операции фильтрации, идентификации, определения площади и выравнивания времени удерживания пиков. В алгоритме обнаружения пиков используется метод согласованной фильтрации с применением в качестве фильтра второй производной гауссовой модели формы пика. Величина порога выбирается по уровню отношения сигнал/шум. Ширина пика определяется по точкам пересечения нуля отфильтрованных данных в зоне пика.

В пакете MetSign [4] обнаружение пиков производится по пересечению нулевой линии первой и второй производной хроматограммы. На основе модели в виде экспоненциально-модифицированной гауссианы выполняется уточнение параметров пиков методом подгонки кривых.

Программные пакеты MetAlign [5] и MZmine [6] выполняют коррекцию базовой линии, фильтрацию шума и артефактов в спектре масс, детектирование пиков, нормализацию, формирование таблиц пиков, визуализацию результатов.

В статье [7] авторы используют популярный фильтр Савицкого—Голея для вычисления производных первых трех порядков в скользящем окне данных. По первой производной определяют зоны пиков по шкале времени хроматограммы. Если величина отрицательной области второй производной превышает порог, пик считается обнаруженным. По числу пересечений нулевой линии третьей производной в зоне пика судят о наличии или отсутствии неразделенных соседних пиков. Значения времени удерживания, амплитуды и ширины пика определяются по данным, полученным из второй производной сигнала.

В работе [8] авторы используют вторую производную гауссовой кривой, взятую с обратным знаком ("мексиканская шляпа"), в качестве ядра оператора для вычисления сглаженной второй производной хроматографического сигнала. Обнаружение пика производится по превышению второй производной порога, равному 10-кратной интенсивности шума. Интенсивность пиков определяется в точках максимума по интенсивности норми- рованной второй производной храматограммы, время удерживания — по положению максимумов на временнόй шкале и, наконец, ширина пиков — по разности между временами окончания и начала пиков на уровне, равном 3-кратной интенсивности шума.

В работах [9, 10] используется функция "мексиканская шляпа" в качестве материнского вейвлета для непрерывного вейвлет-преобразования (НВП) данных. Выполняя НВП при различных величинах масштаба материнского вейвлета, получают двумерный спектр на плоскости вре-мя/масштаб, содержащий на каждом масштабе (шкале) пики, порожденные исходными данными. Максимумы пиков, положения которых близки, формируют хребты, объединяющие эти максимумы по всем шкалам. Пик считается обнаруженным, если сумма его максимальных значений по шкалам (по хребту) превышает заданный порог. Положение пика определяется по отсчету при минимальном значении масштаба. Благодаря применению НВП в широком диапазоне масштабов метод позволяет разделить близкие пики без заметной седловины между ними. Точные значения параметров пиков определяют методом подгонки кривых. Применение "мексиканской шляпы" и вообще второй производной данных позволяет, кроме того, удалить базовую линию, линейную в пределах окна дифференцирующей функции.

Алгоритм детектирования пиков в тандеме (газовый хроматограф—спектрометр ионной мобильности) (GC-IMS) [11] основан на вычислении первой и второй частных производных двумерных данных. Величины интенсивности, гауссовой кривизны и матрицы Гессе в каждой точке двумерной поверхности сравниваются с соответствующими порогами, по результатам чего принимается решение о наличии пиков.

Таким образом, существующие методы оценки параметров пиков в той или иной степени используют дифференцирование исходных (сырых) данных. В настоящей работе предлагается алгоритм, в котором с целью повышения надежности обнаружения особенностей сигналов, имеющих вид пика на фоне шумов, используется метод вычисления производных не в одной, а в трех точках скользящего окна данных для принятия решения о наличии пика и оценки его параметров.

ТЕОРИЯ

Данные аналитических приборов y ( t ) многокомпонентного анализа веществ можно представить в виде аддитивной смеси K пиков { x k ( t ) , k = 1,..., K } , например, гауссовой формы

1.5

0.5

И

S

м,„ if ii i <■ t in

-0.50

0.5

1.5

Номер отсчета i (× 10⁴)

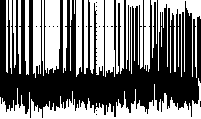
Рис. 1. Модель аналитического сигнала, состоящий из ста пиков гауссовой формы при отношении сиг-нал/шум 2.5.

Ширина пиков линейно возрастает с увеличением i и шума n (t) (предполагается, что базовая линия удалена):

y (t ) = 2X ( t ) + n ( t ) ,

k = 1

где x_k ( t ) = A_k exp { - ( t - t_k ) 2 j Ц2Д ; t — непрерывное или дискретное время t = iSt ( i = 1,2,..., N ), N — число отсчетов данных, δt — интервал дискретизации; A_k , t_k , µ_k — интенсивность, положение и среднеквадратическая ширина k -го пика. Пример такого аналитического спектра, состоящий из ста пиков гауссовой формы с добавлением белого шума, приведен на рис. 1.

Массив дискретных данных y (iSt) = y (i) образует N -мерный вектор y = (y (1),y (2),-,y (N)).

Сформируем текущую выборку из M + 1 отсчетов с центром в точке i исходных данных:

Y w = ( y w ( ¹ ) , y w ( ² ) ,-, y w ( ^M /2 ) ,-, y w ( ^{M + 1} ) ) =

= ( y (i- M/2),..., y (i),..., y (i + M/2)), где M выбирается всегда четным из условия 0.5 ^ 0.7 от ширины пика на половине высоты в отсчетах. При этом во избежание скачков на границах массива у, полагаем, что если i - M/2 < 0, то yw (i - M/2) = y (1), и если    i + M/2 > N, то yw (i+ M/2) = y(N).

Номер отсчета i (× 10⁴)

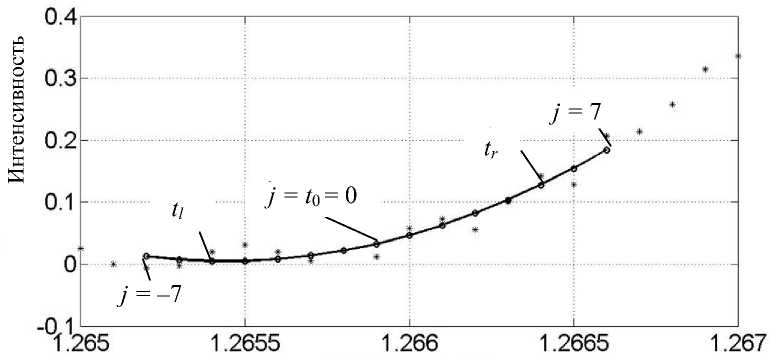
Рис. 2. Аппроксимация данных полиномом второго порядка в скользящем окне из 15 точек ( M = 14) на сетке ( j= –7,…, j= 0,…, j= 7).

t_l , t ₀ , t_r — точки аппроксимирующей параболы, в которых вычисляются первые производные

Аппроксимируем отсчеты в окне yw полиномом второй степени (параболой) на сетке j = (-M /2,...,0,..., M Jiy ных данных в точке i

y (i ) = y (0 ) = p 3.

y ( ^j ) = P 1 ^{j 2} + P 2 ^j + P 3 ,

где p ₁ , p ₂ , p ₃ — коэффициенты полинома.

Выберем в интервале

MM

2,2

три точки

t_t , t ₀, t_r ( I — left, r — right) такие, что t_l = j =

M

ОПИСАНИЕ АЛГОРИТМА

Используя формулы (1), (2), (3) рассмотрим алгоритм обнаружения пиков и их параметров. В начале обработки исходных данных по этим формулам в программе устанавливаются признаки обнаружения начала и вершины пика:

—

, t 0 = j = 0 t r = j =

M

, где

M

целое число, большее или равное M 4 . На рис. 2 показан фрагмент спектра с окном данных из пятнадцати отсчетов ( M = 14) и аппроксимирующая парабола с точками t_l , t ₀ и t_r .

Величина первой производной параболы в точке t_l будет равна

^d l = ² P 1 t l + P 2

PS =

0, пик отсутствует,

1, начало пика обнаружено.

0, вершина пика не обнаружена,

1, вершина пика обнаружена.

Условие начала пика имеет вид dl > 0; dr > ths!ope; P 3 > th min и PS = 0,      (4)

PSS =

и в точке t_r :

d r = ² P 1 t r + P 2 .                        ⁽²⁾

Величина второй производной параболы равна p ₁ .

Величина параболы в точке j = 0 равна усредненному значению в скользящей выборке исход- где thmin — порог нижнего уровня, выбираемого по стандартному отклонению шума σ, th mm = (1 ^ 2) ° , thsiope — порог по наклону фронта пика, для гауссовой формы пика выбирается из интервала thslope = 0.003 ^ 0.007 .

После обнаружения начала пика устанавливаются признаки PS = 1 и PSS = 0.

Номер отсчета i (× 10⁴)

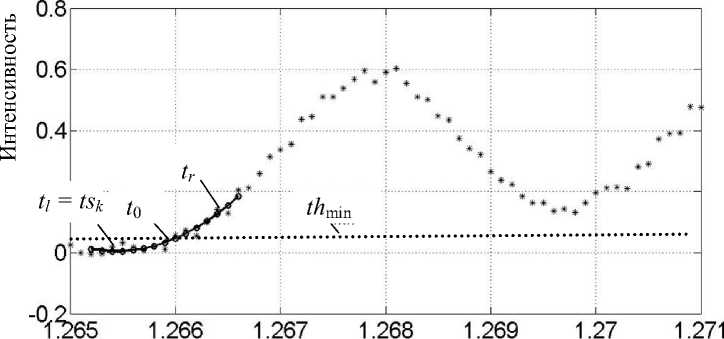
Рис. 3. Фрагмент спектра с аппроксимирующей параболой (утолщенная линия) в начале пика.

th _min — порог нижнего уровня; ts_k — начало пика

Номер отсчета i (× 10⁴)

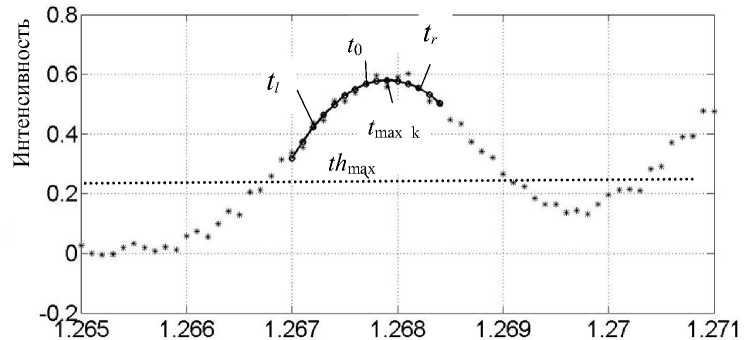
Рис. 4. Фрагмент спектра с аппроксимирующей параболой (утолщенная линия) на вершине пика.

th _max — порог максимального уровня; t _{max k} — положение вершины k- го пика

Начало k -го пика определяется по положению точки t, на шкале отсчетов i : ts k = arg ( t l ) i при условии PS = 1 (см. рис. 3).

Условие вершины пика имеет вид

PS = 1; d >  0; d r <  0; p 1 <  0 и max ( y ) > th m _ax, (5)

где thmax — порог максимального уровня, выбираемый из условия thmax = (4 ^ 6) ^ .

Оценка амплитуды A ^ˆ _k и положение вершины t _{max_ k} k -го пика определяются по точке максимума i _max параболы:

A k = ^max ( y ) , t max_ k = ^arg ( ^max ( y ) ) i            ⁽⁶⁾

по шкале отсчетов i (см. рис. 4).

С целью повышения точности определения параметров пика необходимо, чтобы середина параболы i = i0 располагалась ближе к вершине пика на удалении от нее, например, максимум на два отсчета. Для этого к условию (5) следует добавить условие abs (tmxk — iо )< 3.

После обнаружения вершины пика устанавливаются признаки PS = 0 и PSS = 1.

Оценку ширины пика на половине высоты находим из условия равенства участка гауссовой модели в окрестности вершины пика и аппроксимирующей ее параболы (полагаем переменную t непрерывной):

A_k exp ‘

t — t z-max_ k v M.

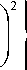
= p_x t²

+ p 2 t + p 3

= y ⁽ t ) .

В точке t_l параболы имеем

A l _k exp <

( L - f l max_ k v   Mk

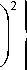
= y (tl ) .

Прологарифмировав обе части равенства и выполнив преобразования, получим

M k = I t l

t max_ k ln

( A A

IJ

.

Ширина пика на половине высоты будет равна

MV2_k = V2ln2 Цk .(7)

Площадь k -го пика гауссовой формы определяется по формуле

Sk = ПА .Ak Mk(8)

Условия конца пика имеют следующий вид: если

PSS = 1; di < 0; dr < 0; p3 < thmm,(9)

то обнаружен одиночный (хорошо разделенный) пик.

При этом конец k -го пика определяется по положению точки t_k на шкале отсчетов i : tf_k = arg ( t_k ) i ; устанавливается признак: пики разделены R_k = 1 (при условии R_{k —} j ^ 0) и признак PSS = 0.

Если условие (9) не выполняется, но выполняется условие

PSS = 1; d i <  0; d r > th _stope; p 3 >  th „,., (10) то обнаружена седловина между соседними пиками.

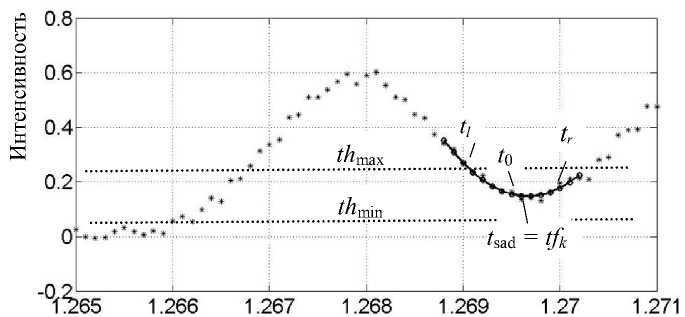
При этом конец k -го пика tf_k определяется по положению точки минимума параболы в седловине между пиками t _sad = arg ( min ( y ) ) по шкале отсчетов i : tf k = arg ( t sad ) i (см. рис. 5).

Номер отсчета i (× 10⁴)

Рис. 5. Фрагмент спектра с аппроксимирующей параболой (утолщенная линия) на седловине пика.

t _sad — положение седловины между пиками; tf_k — конец пика

Если при этом выполняется условие, например, У ( tsad )>= 3 Ak , т. е. если глубина седловины не превышает одной трети интенсивности пика, то можно считать, что соседние пики не разделены и устанавливается признак Rk = 0. В противном случае устанавливается признак Rk = 1.

Таким образом, в результате выполнения алгоритма детектирования последовательности пиков по приведенному выше алгоритму имеем оценки следующих параметров каждого пика:

– начало ts_k ,

– положение максимума t _{max_ k} ,

– интенсивность A ^ˆ _k ,

– площадь S ^ˆ _k ,

– конец tf_k ,

– признак разделения R_k .

МОДЕЛИРОВАНИЕ пиков гауссовой формы с добавлением белого шума (рис. 1) путем сравнения результатов обработки с алгоритмом, приведенным в работе [12]. Относительная погрешность оценки амплитуды, ширины и площади пиков производилась по десяти реализациям шума путем вычисления СКО параметров каждого пика и деления его на истинное значение параметра. Погрешность положения пика определялась по его отклонению от истинного значения. Максимальные значения погрешностей для обоих методов обработки сведены в таблицу. Кроме того, вычислялась вероятность правильного обнаружения как отношение числа обнаруженных пиков по всем десяти реализациям, положение которых отличается от заданных в модели не более, чем на четыре отсчета, к общему числу модельных пиков. Вероятность ложного обнаружения вычислялась как отношение числа обнаруженных пиков по всем десяти реализациям, не заданных в модели, к общему числу модельных пиков. Сравнение столбцов 1 и 2 таблицы показывает явное преимущество предлагаемого алгоритма как по уровню погрешности оценки параметров пиков, так и по величине вероятности ложного обнаружения.

Проверка эффективности алгоритма производилась по модельному спектру, состоящему из 100

Абсолютные (для положения пиков) и относительные среднеквадратические ошибки (СКО) оценки параметров пиков при различных отношениях сигнал/шум для метода, изложенного в [12], — 1 и предлагаемого метода — 2

Параметр	Отношение сигнал/шум
	2.5		5		10		20
	Метод расчета
	1	2	1	2	1	2	1	2
Положение пика (в отсчетах)	3.98	3	1.68	2	0.75	1	0.38	0
Амплитуда	0.08	0.04	0.038	0.018	0.21	0.01	0.01	0.004
Ширина	0.90	0.34	0.46	0.23	0.19	0.13	0.08	0.047
Площадь	1.01	0.27	0.43	0.19	0.18	0.11	0.08	0.030
Вероятность правильного обнаружения	0.980	0.999	1	1	1	1	1	1
Вероятность ложного обнаружения	0.016	0.002	0.003	0.001	0.002	0	0.002	0

ЗАКЛЮЧЕНИЕ

Алгоритм детектирования предложенным методом позволяет повысить достоверность обнаружения пиков благодаря низкому уровню ошибки оценок и вероятности ложного обнаружения при малых отношениях сигнал/шум. Это позволяет значительно понизить порог чувствительности приборов и расширить диапазон измеряемых концентраций.