Метод оценки производительности узлов коммутации для сетей связи следующего поколения

Постановка задачи. Производительность узлов коммутации C , используемых в сетях связи следующего поколения, определяется количеством IP-пакетов, которое обрабатывается в единицу времени (обычно за 1 с). Производители телекоммуникационного оборудования разрабатывают узлы коммутации нескольких типов, которые различаются номиналами производительности, образующими ряд C ₁ , C _{2 ,} , ..., C _L .

Номинал производительности для узла коммутации к -го типа ( C k , к = 1 , L ) должен быть выбран как минимальное значение из всех возможных значений ряда C 1 , C 2 , , ..., C L , удовлетворяющее условию C k ≥ μ , где μ – интенсивность обслуживания IP-пакетов, вычисленная с учетом заданных показателей качества обслуживания в сети связи следующего поколения.

Для оценки интенсивности обслуживания IP-пакетов анализируются два показателя, приведенные в рекомендации Y.1541 [1] Международного союза электросвязи (МСЭ). Во-первых, определяется норма на IPTD (IP packet transfer delay) – среднее время задержки IP-пакетов при их передаче между интерфейсами пользователь – сеть. Во-вторых, задается значение IPDV (IP packet delay variation), которое определяет вариацию времени задержки IP-пакетов. Для расчета этого параметра из 0 , 999 -го квантиля функции распределения (ФР) времени задержки IP-пакетов t P вычитается величина минимально возможной длительности передачи IP-пакетов t _min [1]:

IPDV = t p - t min .

Норма на IPTD позволяет оценить минимальную величину μ _IPTD , т. е. интенсивность обслуживания, необходимую для того, чтобы средняя задержка IP-пакетов не превышала заданного порога. Аналогично норма на IPDV позволяет найти такое минимальное значение μ IPDV , при котором величина вариации задержки IP-пакетов соответствует заданным требованиям. Зная эти две величины, можно найти интенсивность μ :

Ц = max ^{ц iptd , ц ipdv ^}.

Таким образом, поставленная задача сводится к оценке величин μ _IPTD и μ _IPDV . Для решения этой задачи целесообразно использовать математический аппарат теории телетрафика [2]. Узел коммутации рассматривается в качестве системы массового обслуживания (СМО), поступающие IP-пакеты представляют собой поток заявок.

Оценка величины μ IPTD . В [3] получены выражения для расчета кумулянтов n -го порядка времени ожидания начала обслуживания IP-пакетов в узле коммутации W _n ^C . Кумулянт первого порядка W ₁ ^C равен среднему значению времени ожидания. Время обработки IP-пакетов B может считаться постоянной величиной. Обычно тракт обмена IP-пакетами между интерфейсами пользователь – сеть состоит из N узлов коммутации. В каждом i -м узле коммутации для средних значений времени ожидания и обслуживания следует использовать обозначения c индексом i . Все IP-пакеты, в дополнение ко времени пребывания в узлах коммутации, задерживаются на постоянное время T _N , определяемое в основном длительностью распространения сигнала. Значение IPTD определяется суммой

NN

IPTD = T n + ^ W C ( i ) + ^ B ( i ) .                     (1)

i =1             i =1

Величины W C ( i ) определяются на основе двух распределений: A i ( t ) и B i ( t ) . Функция A i ( t ) описывает распределение длительности интервалов между моментами поступлений соседних заявок для i -го узла коммутации. Функция B i ( t ) представляет собой распределение времени обслуживания в i -м узле коммутации. Для анализа i -го узла коммутации достаточно использовать время обслуживания, которое связано с величиной ц _IPTD ( i ) простым соотношением [2]

B ⁽ i ) = — .

Ц IPTD ⁽ i )

Для получения оценки μ IPTD целесообразно предположить, что параметры трафика для всех узлов коммутации идентичны. Тогда выражение (1) можно упростить:

N

IPTD = T n + NW ? ( A ( t ) ,ц iptd ) +----- .                     (2)

μ IPTD

Вид и параметры функции A ( t ) определяются по результатам измерений обслуживаемого трафика, значение T N выбирается для максимальной длины устанавливаемого соединения, а величина IPTD задана нормами МСЭ. Таким образом, в выражении (2) неизвестной величиной является только μ _IPTD . Искомая величина находится численно из соотношения (2). Выражение для функции W C ( A ( t ) ,ц _IPTD ) в формуле (2) приведено в работе [3].

Оценка величины μIPDV. В рекомендации МСЭ Y.1541 [1] приведена методика оценки 0,999-го квантиля ФР времени задержки IP-пакетов. Данная методика позволяет рассчитать значение tP , входящее в формулу для вычисления показателя IPDV. Оценка величины tmin выполняется с учетом постоянных задержек, детерминированных для сетей с известной структурой, и представляет собой достаточно простую последовательность арифметических действий. Вычисление квантиля tP , наоборот, является сложной задачей.

Следует отметить, что в [1] не приводится оценка точности предложенного метода. Поэтому до разработки принципов расчета величины μ _IPDV следует оценить погрешность, которая возникает при вычислении квантиля с помощью метода, рекомендованного МСЭ. При использовании данного метода предварительно оцениваются среднее значение t s ( i ) и среднеквадратичное отклонение a s ( i ) времени задержки заявок на каждой i -й фазе обслуживания, т. е. в каждом узле коммутации. Кроме того, в результате измерений для i -й фазы получено значение квантиля t p ( i ) . В [1] значение p , для которого нормирован квантиль, равно 0,999. Помимо указанных параметров определяется значение x _P , представляющее собой значение p -квантиля для стандартного нормального распределения [4].

Далее вычисляется асимметрия времени задержки заявок на i -й фазе обслуживания y ( i ) • Формулу для расчета асимметрии можно представить в виде [1]

Y ( i ) = 6

x p - [ t p ( i ) - t s ( i )] /a s ( i ) 1 — ( x p ) ²

Третий центральный момент исследуемой случайной величины на i -й фазе обслуживания ш ( i ) определяется следующим образом [1]:

^{ш (} i ) = Y ⁽ i ^{)[ a} s ⁽ i ^)] 3 •

Для маршрута, содержащего N фаз, необходимо найти среднее значение t S , дисперсию σ _S ² и асимметрию γ времени задержки. Эти параметры вычисляются по формулам [1]

NN ts = £Ы i), aS = £a| (i), i=1                 i=1

Y =

(? - 4/

( a s ) ³ •

Согласно [1] p-квантиль ФР времени задержки в СМО из N фаз определяется соотношением tP = ts + as (xp - l^L-^) • (6)

Проверку точности метода расчета t P , рекомендуемого МСЭ, целесообразно провести для ряда моделей многофазной СМО, которые позволяют найти точные значения квантиля случайной величины. Практический интерес представляют ФР с возможными значениями на положительной полуоси. В ряде случаев допустимы сколь угодно большие значения времени t . В данной работе соответствующие ФР F и ( t ) называются распределениями класса U (unbounded, т. е. неограниченные).

Некоторые модели можно исследовать с помощью распределений F ( t ) , для которых возможные значения заданы на ограниченном интервале времени. Для них также справедливо условие t >  0 . Соответствующие ФР F в ( t ) называются распределениями класса B (bounded, т. е. ограниченные). Распределения класса B полезны для исследования многофазных СМО, в которых задано максимально возможное время пребывания заявок t max .При t>t max функция F в ( t ) равна единице. Другое применение распределений класса B основано на использовании статистических данных, при сборе которых никогда не были зафиксированы значения времени пребывания заявок, превышающие t _max .

Из распределений класса U целесообразно выбрать многофазную СМО, состоящую из систем типа M/M/ 1 (классификация Кендалла) [2]. Для такой модели по известным величинам интенсивности входящего потока заявок λ и их обслуживания μ несложно найти ФР времени задержки заявок, которые проходят через N фаз:

N - 1 N - j - 1

F u ⁽ t ) = ¹ - e - ⁽ - " ' t £ ^|(** _N - >  - 1), . (7)

Если во всех фазах величины λ и μ различаются, то формула для вычисления искомой ФР становится более громоздкой, но ее вывод не вызывает затруднений. В настоящей работе случай различных величин λ и μ на каждой фазе обслуживания не рассматривается, что не оказывает влияния на конечный результат – оценку точности метода, предложенного МСЭ для расчета квантиля ФР времени задержки заявок.

Для распределений класса B случайная величина задана на отрезке времени ( t min , t max ) . Можно считать, что t min = 0 . Для других значений t min исследуемое распределение можно сдвинуть по оси времени, так чтобы выполнялось условие t min = 0 . В этом случае вместо значения t _max следует использовать разность t _max - t _min .

В ряде случаев функция F в ( t ) может быть представлена с помощью равномерного закона распределения случайной величины. Предположим, что заявки проходят через N фаз с равными значениями величины t max , обозначаемой далее через x . В этом случае необходимо найти распределение случайной величины t , равной Nx . Для каждой фазы ФР времени задержки определяется преобразованием Лапласа - Стилтьеса ф ( s ) вида [5]

(         1

ф ⁽ s ) = -

-

e xs

.

xs

Для нахождения ФР исследуемой суммы случайных величин следует использовать правило свертки изображений [5]

(

- e xs xs

)

N

E ( - 1) i C N e "*“ i =0

( xs ) N

На основании первой теоремы смещения [5] оригинал от правой части выражения (8) представим в форме

F b ( t ) =

N ! x ^N

tN, tN - CN (t - x) N,

E1 (-1) iCN■(t - ix) i, i=0

N ! x N ,

0 < t < x, x < t <  2 x,

( N - 1) x < t < Nx, t≥ Nx.

Если величины t max для всех фаз не идентичны, то оригинал функции ф ( s ) будет представлен более громоздким выражением, но характер кривой F в ( t ) при этом не меняется.

В табл. 1 для рассматриваемой функции F и ( t ) приведены значения относительных ошибок, возникающих при расчете квантиля. Точное значение квантиля определяется из выражения (7). В первой строке табл. 1 приведены величины относительных ошибок, возникающих при использовании метода расчета квантиля, рекомендованного МСЭ. Эти ошибки

Ошибки при расчете квантиля для функции F и ( t )

Таблица 1

Метод расчета квантиля при F U ( t ) = 0 , 999	Количество фаз обслуживания IP-пакетов, %
	N = 3	N = 5	N =7
Рекомендуемый МСЭ	0,9	0,7	0,7
Гамма-распределение	6,3	4,6	4,2
Ряд Эджворта	2,6	2,0	1,6

Ошибки при расчете квантиля для функции F в ( t )

Таблица 2

Метод расчета квантиля при Fи(t) = 0,999 Количество фаз обслуживания IP-пакетов, % N = 3 N = 5 N = 7 Рекомендуемый МСЭ 5,9 5,7 4,9 Гамма-распределение 24,8 14,4 10,3 Ряд Эджворта 7,8 3,4 2,0 находятся в пределах, допустимых с точки зрения практики проектирования узлов коммутации. Следовательно, метод МСЭ можно считать весьма эффективным. Во второй и третьей строках табл. 1 приведены значения ошибок, возникающих при аппроксимации ФР Fи (t) с помощью гамма-распределения [4] и ряда Эджворта [6]. Использование таких замен функции Fи(t) приводит к росту ошибок, которые тем не менее находятся в приемлемых пределах для инженерных расчетов. Результаты, приведенные в табл. 1, получены для нагрузки каждой фазы ρ, равной 0,5. Величина ρ определяется по формуле [2]

Р = ".

μ

В табл. 2 приведены значения относительных ошибок, имеющих место при расчете квантиля для функции F в ( t ) . Во второй и третьей строках указаны относительные ошибки, обусловленные аппроксимацией функции F B ( t ) с помощью гамма-распределения и ряда Эджворта. Анализ данных, приведенных в табл. 2, позволяет сделать вывод, что метод, рекомендуемый МСЭ, позволяет рассчитывать 0,999-й квантиль с точностью, приемлемой для инженерных расчетов. Следует отметить, что при увеличении количества фаз обслуживания более точным становится метод расчета квантиля, основанный на ряде Эджворта. Из табл. 1, 2 следует, что при увеличении количества фаз обслуживания ошибка в оценке квантиля уменьшается.

Соотношения (3)-(6) позволяют решить поставленную задачу – найти такое значение μ IPDV , при котором разность t P - t min равна нормированному значению IPDV. Как и выше, целесообразно считать, что параметры трафика на всех фазах обслуживания идентичны. Параметры, необходимые для оценки μ IPDV , приведены в [3]. Исключением является квантиль t p ( i ) .

Оценка квантиля t p ( i ) . Судя по численным оценкам, приведенным в табл. 1, 2, с ростом количества фаз, через которые проходят заявки (IP-пакеты), точность аппроксимации повышается. Однако найти аппроксимацию, которая становится приемлемой для одной фазы, не удается. Это усложняет применение метода МСЭ для планирования сети, т. е. в тех случаях, когда значение t _p ( i ) невозможно измерить.

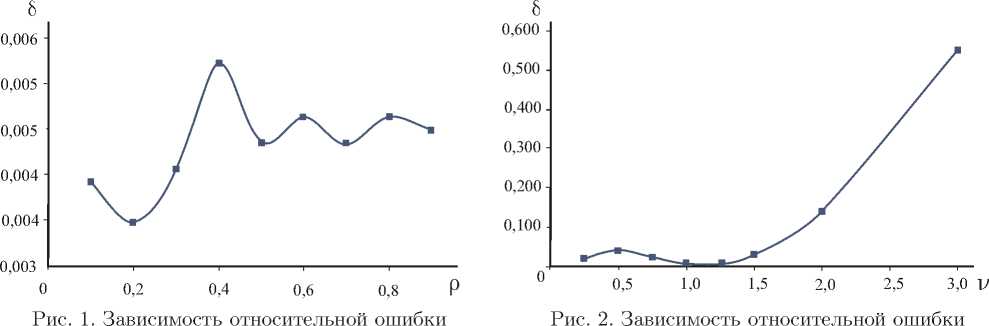
в расчете квантиля от нагрузки            в расчете квантиля от коэффициента вариации

Для определения величины tp (i) можно использовать результаты работы [3], в которой получены кумулянты времени ожидания заявок в СМО с произвольным характером входящего потока заявок и постоянным временем их обслуживания. Для систем с постоянным временем обслуживания заявок кумулянты времени задержки вычисляются элементарно. Тогда для одной фазы обслуживания можно считать известными следующие три параметра времени задержки заявок: среднее значение, среднеквадратичное отклонение и асимметрию. Далее из формулы (3) несложно получить соотношение для расчета квантиля tp(i) = .S(i)xp + SS(i) - "S(i)Y(i><1 - (xp)2). (9) 6

Для оценки точности предложенного способа расчета квантиля проведены вычисления точного значения t p ( i ) для некоторых законов распределений. На рис. 1 показана зависимость относительной ошибки δ в расчете квантиля для экспоненциального распределения времени задержки IP-пакетов от нагрузки. Очевидно, что величина ошибки находится в допустимых пределах, т. е. соотношение (9) может быть использовано для оценки квантиля t p ( i ) для одной фазы обслуживания. Это утверждение справедливо, если распределение времени задержки подобно экспоненциальному, для которого коэффициент вариации равен единице.

На рис. 2 приведена зависимость относительной ошибки в расчете квантиля t p ( i ) от коэффициента вариации времени задержки IP-пакетов v . В качестве аппроксимации ФР времени задержки IP-пакетов выбрано распределение Вейбулла – Гнеденко [4]. Выбор распределения обусловлен тем, что для него коэффициент вариации изменяется в широком диапазоне. Из рис. 2 следует, что в интервале изменения коэффициента вариации от нуля до примерно двух относительная ошибка в оценке квантиля приемлема для инженерных расчетов. Для распределений с большим значением коэффициента вариации целесообразно разработать более точный метод расчета квантиля.

Заключение. В данной работе предложен метод оценки производительности узлов коммутации, предназначенных для использования в сетях связи следующего поколения. Величина производительности узлов коммутации должна выбираться таким образом, чтобы выполнялись два ограничения, установленные МСЭ на параметры времени задержки IP-пакетов при их передаче между двумя интерфейсами пользователь – сеть. Получены все соотношения, необходимые для вычисления производительности узлов коммутации.