Метод оценки размеров базовых элементов структур отсканированных цифровых изображений

В ряде задач анализа изображений документов [1] используются образцы, полученные путем сканирования документов, напечатанных полиграфическим способом. Очевидно, такие образцы обладают рядом искажений, вызванных процессом печати-сканирования: зашумленность, геометрические искажения, размытие, погрешности дискретизации и квантования и др.

Как показано в [2], влияние этих искажений может быть уменьшено путем использования сканирующих устройств заведомо большего разрешения, нежели разрешение полиграфического устройства, которым были напечатаны используемые документы. Однако в этом случае неизбежно масштабирование базового элемента структуры анализируемых изображений, вследствие которого некоторые процедуры их обработки, в частности, обработка скользящим окном заданного размера, будут давать не вполне корректные результаты.

Для решения данной проблемы необходимо предварительно оценить коэффициент масштабирования базового элемента структуры в результате цикла печати-сканирования. Если известна линиату-ра (плотность полиграфического растра) печатающего устройства, то решение этой задачи не представляет трудностей, однако в ряде случаев линиа-тура не известна, и задача требует специальных методов компьютерного анализа, один из которых и предлагается в настоящей работе.

Для удобства терминологии введем понятие цифровой линиатуры как коэффициента увеличения геометрических примитивов в результате процесса печати-сканирования. Заметим, что численно цифровая линиатура будет равна размеру минимальных базовых элементов изображения в пикселях. В дальнейшем мы будем понимать под линиатурой не физическую, а именно цифровую линиатуру. Пользуясь данной терминологией, можно сформулировать поставленную задачу как оценку линиатуры отсканированного цифрового изображения.

Существующие методы оценки размеров базовых элементов изображения основаны, большей частью, на концепции обработки изображений с мультиразрешением (Scale Space Image Processing). Наиболее детально разработанный алгоритм, основанный на данном подходе, описан в [3]. Однако, несмотря на универсальность и отсутствие серьез- ных ограничений, накладываемых на тип анализируемого изображения, практическое применение данного алгоритма ограничено из-за высокой вычислительной сложности. Кроме того, данный алгоритм является итерационным, и время его работы линейно зависит от размера базовых элементов структуры анализируемого изображения.

Целью данной работы является разработка прямого однопроходного алгоритма, позволяющего оценивать величину линиатуры.

Общая идея алгоритма

Большинство сканеров на выходе дают полноцветное RGB-изображение. Поскольку для решения задачи оценки линиатуры не представляет интереса не только цвет, но и яркость точек изображения, на предварительном этапе необходимо преобразовать изображение к бинарному.

Предлагаемый метод основан на подсчете статистики длин серий одинаковых (в бинарном случае – черных) пикселей при горизонтальном и вертикальном проходе изображения. В дальнейшем мы исходим из предположения, что максимуму этой статистики (наиболее часто встречающейся длине серии) будет соответствовать значение линиатуры, то есть фактически размера базового элемента структуры в пикселях. Однако данный подход влечет за собой некоторые трудности, вызванные, к примеру, попаданием в статистику «посторонних» серий, соответствующих краевым участкам объектов на изображении.

Рисунок 1 иллюстрирует описанную выше проблему. Светлым цветом выделены горизонтальные серии черных точек, положение которых дает основание полагать о близости их длин с искомой ли-ниатурой.

Рис. 1. Горизонтальные серии, которые должны попадать в статистику

По приведенному на рисунке фрагменту можно сделать вывод о необходимости введения дополнительного условия, характеризующего пространственное положение серии относительно базовых элементов изображения, при соблюдении которого следует учитывать серию в статистике. В качестве такого условия можно использовать условие близости локальных полей направлений в точках начала и конца серии.

Под локальным полем направлений в точке будем понимать направление на область наибольшего скопления черных пикселей в некоторой окрестности данной точки. На рис. 2 стрелками обозначены направления для некоторых серий изображения, представленного на рис. 1 (большими стрелками обозначены близкие направления, а маленькими – существенно различающиеся).

Рис. 2. Локальные поля направлений на концах горизонтальных серий

Как видно из рисунка, дополнительное условие является достаточным для того, чтобы в статистику не попадали «лишние» серии. Таким образом, предлагаемый метод основывается на подсчете статистики длин серий с учетом вычисленных локальных полей направлений. В последующих разделах приводится детальное описание алгоритма.

Метод оценки направления в окне

Известно множество методов построения поля направлений [4, 5]. Однако для оценки линиатуры необходимо посчитать не все поле направлений для изображения, а лишь локальное поле направлений в точках начала и конца серий, в окрестности которых, как правило, находится примерно одинаковое количество черных и белых пикселей. Поэтому в данном случае оно определяется как направление из центра окна на центр масс черных точек в локальном окне. Размер окна выбирается равным n = min {Lwhite , Lblack } , где Lblack – длина текущей черной серии, а Lwhite – длина ближайшей белой серии. На n накладываются дополнительное ограничение сверху и снизу, чтобы избежать с одной стороны излишне грубых оценок, а с другой – лишних вычислений. В данной работе использовалось ограничение n e [7,30].

Оценка влияния погрешностей на вычисление направления

В предыдущих разделах говорилось о том, что серия учитывается в статистике в случае близости направлений в начале и конце серии. Очевидно, критерий близости направлений будет определяться погрешностью оценки локального поля направлений s i в точке с координатами ( i , j ) (где i - номер строки, а j – номер столбца), которая зависит от размера окна n j и распределения шума р в этом окне:

^s j =^s ( i , j , n j , p ( i , j , n j

.

Тогда критерий близости направлений в точках ( i , j ) - начала серии - и ( i , j + L_black ) - конца серии (при горизонтальном проходе изображения) – выглядит следующим образом:

d — d , ij j ⁺ L black

8      U ⁺ L black ’

где d _ij – локальное поле направлений в точ ке (i , j ).

Определим приближенно зависимость (1) для модели печати-сканирования. Предположим, что исходное изображение в результате этого процесса было подвергнуто зашумлению. Далее в расчетах будем исходить из модели импульсного шума, а также будем считать, что s =s n =s ij ij n , т.е., исходя из предположения о слабой зависимости погрешности от положения центра окна, заменим значение интенсивности шума в окне его средней интенсивностью на всем изображении.

При большом размере окна импульсный шум не искажает поле направлений, так как он равномерно распределен по всему окну. Оценим возможность неравномерного распределения пикселей шума внутри окна. Пусть X - базовая вероятность в модели импульсных помех. Далее будем рассматривать распределение величины 1 L_k , где L_k – расстояние

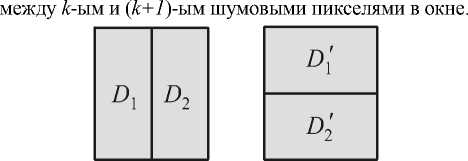
Рис. 3. Взаимное расположение областей в окне

Рассмотрим выборки данной величины для областей D 1, D2, D1 , D2 внутри окна (рис. 3). Объем выборок примем равным 1/2, n2 X , где n - размер окна. Так как характеристики импульсного шума одинаковы для указанных областей, то должна выполняться статистическая гипотеза о равенстве математических ожиданий MD1=MD2 л MD1,=MD2, при заданном α, что равнозначно выполнению гипотезы MD1=MD2 при α′ = α.

Необходимо определить максимальное

^{∆ M} noise ^{= M}D 1 ^{- M}D 2 , которое не вызовет отклоне- noise         D 1 D 2

ния описанной выше статистической гипотезы. Оценка ожидаемого количества «шумовых» пикселей может быть определена как

noise

⁼¹ 2 ^{n 2 ⋅ ∆ M} noise ^.

На основании вычисленного значения L ста-noise новится возможным оценить ошибку, возникающую при вычислении центра масс. Полагая, что связь между Lnoise и ошибкой при вычислении центра масс является линейной, получим относительную погрешность ε′n = Lnoise Nblack , где Nblack – число черных пикселей в окне, которое может либо вычисляться для каждого конкретного окна, либо приниматься равным среднему значению Nblack = 12n2 . В этом случае

Учет направления серий при оценке линиатуры

Серии, учитываемые в статистике, могут пересекать объекты на изображении под разными углами в зависимости от их ориентации и от поворота документа при сканировании. Так как изображение обрабатывается дважды – в вертикальном и горизонтальном направлении, то в худшем случае длины серий могут увеличиться в max sin α= 2 раз.

α ∈ [ 0;π 2 ]

На рис. 4 темными линиями показаны серии при двух проходах изображения, а светлой линией – ре-

альная линиатура.

_{′ =} ^Lnoise n

Nblack

2L noise

2 ^, n ²

L noise

₌ ς n ² noise   _{2 n} J λ ^,

где ∆ M_noise – допустимая разность математических ожиданий для областей D 1 , D 2 .

Упрощенная оценка по критерию Уэлча

∆M   =ς , где ζ – некая константа, не завися- nλ

щая от объема выборки. Поэтому

π

ε= ⋅ε′ n2n

πς

2 n Vλ

– погрешность для углов, измеряемых в радианах. Правая часть равенства (3) содержит неизвестную константу, определяемую э мпи рически и зависящую от характеристик печатающего и сканирующих устройств. В частности, на основе эмпирической оценки количества «шумовых» пикселей для окна конкретного заданного размера было выбрано значение ςλ≈ 0, 25 , и получена приблизительная оценка

ε

n

π

8 n

Рис. 4. Линиатура и длины серий

Для получения минимального значения линиату-ры необходимо корректировать длины серий, участвующих в статистике, с учетом угла между преобладающим направлением в точках серии и направлением развертки. Преобладающее направление серии определяется как среднее арифметическое направлений на ее концах.

При проведении экспериментов использовались два способа коррекции длин серий:

• а)    для каждой серии,

• б)    для групп серий одной длины.

Способ (а) методологически является более корректным, однако, как показали эксперименты, не является устойчивым к ошибкам оценки направлений. Мотивацией для использования способа (б) является априорная информация о наличии преобладающей ориентации объектов на большинстве изображений исследуемого класса (рис. 5), вследствие чего можно установить приближенное соответствие между длинами серий и их ориентацией. Этот способ ввиду усреднения направлений дает результат, более стойкий к погрешностям их вычисления.

Сделанные упрощения не позволяют дать точную оценку абсолютной погрешности (фактически, точная оценка заменена значением ζ , выбираемым в зависимости от предполагаемой интенсивности импульсного шума), но позволяют учесть изменение абсолютной погрешности при изменении размера окна. Зависимость абсолютной погрешности от количества черных пикселей в окне не учтена в данной приближенной оценке, но может учитываться путем вычисления для конкретного окна значения N_black .

пропги женин J МИрО!

Рис. 5. Примеры изображений с ярко выраженным преобладающим направлением объектов

Описание алгоритма

Шаг 1. Преобразование цветового пространства RGB–Lab.

Шаг 2. Обработка L-компоненты:

Шаг 1.2. Адаптивная пороговая обработка.

Шаг 1.3. Поэлементная обработка изображения (цикл по всем пикселям):

Шаг 1.3.1. Выделение серии черных пикселей в строке.

Шаг 1.3.2. Нахождение локальных полей направлений в точках начала и конца серии.

Шаг 1.3.3. При условии близости полей направлений добавление длины текущей серии в статистику, а ее направления – в отдельную статистику.

Шаг 2.3. Нахождение длины серии с максимальным значением статистики.

Шаг 2.4. Транспонирование изображения.

Шаг 2.5. Повторение пунктов 2.2-2.3 для транспонированного изображения (новая статистика).

Шаг 3. Нахождение минимальной из двух найденных длин серий.

Шаг 4. Линиатура равна полученной длине серии, помноженной на косинус соответствующего ей направления.

Вычислительный эксперимент

При проведении эксперимента использовались отсканированные изображения документов, напечатанных различными устройствами печати.

• M*eciee c£™ ’"“° “

■ миро*»* wmuthm . eee* ""О^ аы. .ки.хкнно^^«родим*соре»номи рое * iew******”^ ч<ып*ои»тое г на Олимпийс»** "П» «меппжи иепок fc,«обета»"»™Госс. VM

„» , о о“е“*          «от. !■«««•• *

। а(х..е они пом »      Со*к«.<*о Совм. *

Рис. 7. Изображение «Портрет»

таете*. no и жри* и,

ictuepw*M

Рис. 6. Изображение «Текст»

В частности, на рис. 8-9 приведены гистограммы длин горизонтальных серий для изображений на рис. 6-7. Следует отметить, что для изображения на рис. 7, которое было напечатано и отсканировано с высоким разрешением, всплеск статистики пришелся не только на линиатуру, но и на длины серий, кратные линиатуре. Однако для большинства проанализированных изображений гистограмма имеет вид, сходный с гистограммой первого изображения.

Оценка времени работы алгоритма

Очевидно, время работы T предлагаемого алгоритма линейно зависит от общего количества пикселей анализируемого изображения, от количества пикселей, обрабатываемых при подсчете локальных полей направлений, и может быть выражено соотношением:

K

T = a • V • H + b -У (min Lti, ,,L^k ,⁰J\

I [ black , white J /

+ ( mln { ^L_bla_Ck ,

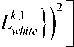
где V , H – ширина и высота изображения, k – порядковый номер черной серии, K – общее количество черных серий, L^k _black – длина k -ой черной серии, L^k _w ^, _h ⁰ _ite – длина белой серии, предшествующей k -ой черной серии, L^k _w ^,1 _hite – длина белой серии, следующей за k -ой черной серией, a и b – постоянные величины.

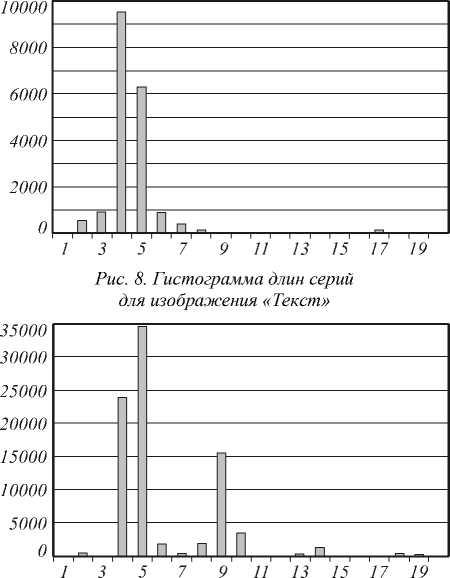
Рис. 9. Гистограмма длин серий для изображения «Портрет»

Очевидно, в силу зависимости размера локального окна при оценке направлений от длин двух серий и невозможности определить общее количество серий и их длины (поскольку в статистику попадают далеко не все), практическая проверка формулы (5) по результатам работы программы невозможна без дополнительных алгоритмических изменений. Однако приближенно время работы алгоритма может быть оценено по формуле:

n max

T ^a- V • H + Р- У S n U 2 ,                    (6)

n = 1

где n – текущая длина серии, n _max – наибольшая анализируемая длина серии, s _n – количество серий длины n, попавших в статистику, a и в - постоянные.

В формуле (6) завышены размеры окна, однако не учитываются не включенные в статистику серии. Как показали сравнения значений времени, полученных по формуле (6), с реальным временем работы программы, эти допущения в некоторой степени «нейтрализуют» друг друга, и оценка получается близкой к экспериментально полученным значениям.

В качестве примера в таблице 1 приведены зна-n чения V⋅ H и ∑ sn n 2 , а также практического Tpr и n =1

теоретического T_tr (по формуле (6) времени для четырех изображений. По первым д вум из них определены коэффициенты α и β из условия равенства T _pr и T_tr , которые затем подставлены в формулы для других двух изображений. Полученные теоретические значения оказались довольно близкими к практическим.

Таблица 1. Расчет времени работы программы

№ изображения	V ⋅ H , пикселей	n max ∑ s n n 2 , n = 1 пикселей	т pr , сек.	т tr , сек.
1	5 719 728	4 394 467	19	19
2	1 444 851	668 581	4	4
3	3 247 200	2 932 689	10	11,5
4	9 606 790	2 932 704	21	23,8

Заключение

В данной работе предложен прямой алгоритм оценки линиатуры отсканированного изображения, базирующийся на подсчете длин серий и вычислении локального поля направлений. Время работы алгоритма линейно зависит от размеров изображения, что существенно меньше времени работы известных алгоритмов решения данной задачи.

Работа выполнена при финансовой поддержке российско-американской программы « Фундаментальные исследования и высшее образование » ("BRHE"), а также грантов РФФИ № 07-07-97610-р_офи, № 07-07-97603-р_офи, № 07-01-96612-р.