Метод оценки текущей и дополнительной нагрузки на систему электрических приводов механизмов параллельной кинематической структуры
Автор: Круглова Т.Н.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 3 т.21, 2021 года.
Бесплатный доступ
Введение. В статье рассматривается проблема нагрузки на систему электрических приводов в параллельной кинематической структуре. Описана задача разработки отказоустойчивой системы, позволяющей выполнять заданный технологический процесс при отказе одного или нескольких приводов. Цель работы - создание метода оценки текущей и дополнительной нагрузки на каждый привод механизма параллельной кинематической структуры. Решение позволяет корректировать режим эксплуатации при выполнении заданного технологического процесса без ущерба для исправных приводов.Материалы и методы. Ранее разработан метод диагностирования, который базируется на расчете и анализе коэффициентов прямых, аппроксимирующих огибающие значений коэффициентов вейвлет-преобразования сигналов тока электродвигателя с учетом характерных масштабов. Это дает возможность определить текущее техническое состояние электродвигателя и найти неисправности. Логическое продолжение данного подхода - предлагаемый метод оценки текущей и дополнительной нагрузки. Он позволяет на основе коэффициентов прямых, аппроксимирующих огибающие вейвлет-коэффициентов токового сигнала, найти текущую нагрузку на привод. Для расчета дополнительной нагрузки учитываются количество и местоположение неисправных приводов.Результаты исследования. Для каждого масштаба вейвлет-коэффициентов определены относительные коэффициенты и текущая нагрузка на каждый привод. Проверена возможность перераспределения нагрузки на два соседних домкрата, исследовано поведение системы в этом случае. Нагрузка, перемещаемая неисправным домкратом, перераспределяется на два соседних домкрата в равных долях - по 14,76 %. Общая нагрузка на приводы - 44,28 %, что безопасно для сервопривода. Нагрузка на привод четвертого домкрата не меняется (29,52 %). Приводы имеют достаточный запас надежности. Установлено, что все три режима эксплуатации допустимы для исследуемого сервопривода, не ведут к динамическим перегрузкам и преждевременному отказу.Обсуждение и заключения. Экспериментальные исследования метода оценки текущей и дополнительной нагрузки показали его адекватность и высокую эффективность. Установлено, что при отключении приводов одной из стоек механизма система выполнила перераспределение нагрузки на приводы. Таким образом удалось избежать их динамических перегрузок и преждевременного отказа. Значит, решение способно обеспечить надежное функционирование комплекса на время ремонтных работ.
Механизм параллельной кинематической структуры, система приводов, оценка текущей и дополнительной нагрузки, вейвлет-преобразование, аппарат нечеткой логики
Короткий адрес: https://sciup.org/142231886
IDR: 142231886 | УДК: 621.8-1/-9 | DOI: 10.23947/2687-1653-2021-21-3-268-274
Method for assessing the current and additional load on the parallel kinematic structure mechanisms electric drive system
Introduction. The problem of the load on an electric drive system in a parallel kinematic structure is considered. The task of developing a fault-tolerant system that provides performing a given process in case of a failure of one or more drives is described. The work objective is to create a method for estimating the current and additional load on each drive of the mechanism of a parallel kinematic structure. The solution enables to correct the operating mode when performing a given process without compromising serviceable drives.Materials and Methods. Previously, a diagnostic method was developed. It is based on the calculation and analysis of the coefficients of straight lines that approximate the envelopes of the values of the wavelet transform coefficients of electric motor current signals, taking into account the characteristic scales. This makes it possible to determine the current technical condition of the electric motor and find malfunctions. The logical continuation of this approach is the proposed method for assessing the current and additional load. It provides finding the current load on the drive based on the coefficients of the lines approximating the envelopes of the wavelet coefficients of the current signal. To calculate the additional load, the number and location of faulty drives are taken into account.Results. For each scale of the wavelet coefficients, the relative coefficients and the current load on each drive are determined. The possibility of redistributing the load to two adjacent jacks was checked; the behavior of the system in this case was investigated. The load moved by the faulty jack is redistributed to two adjacent jacks in equal shares - 14.76 % each. The total load on the drives is 44.28 %, which is safe for the servo. The load on the drive of the fourth jack does not change (29.52 %). The drives have a sufficient safety margin. It is established that all three operating modes are acceptable for the studied servo drive, and they do not cause dynamic overloads and premature failure.Discussion and Conclusions. The experimental studies on the method of assessing the current and additional load have shown its adequacy and high efficiency. It was found that when the drives were disconnected from one of the racks of the mechanism, the system performed a load redistribution on the drives. Thus, it was possible to avoid their dynamic overloads and premature failure. This means that the solution is able to ensure the reliable functioning of the complex at the time of renovation work.
Текст научной статьи Метод оценки текущей и дополнительной нагрузки на систему электрических приводов механизмов параллельной кинематической структуры
Введение. В процессе функционирования механизмов параллельной кинематической структуры возможны отказы одного или нескольких приводов. Среди вероятных последствий: наклон платформы, искривление или заклинивание стойки, недопустимые перегрузки, преждевременный отказ механизма, остановка производства и существенные финансовые потери. Для решения данной проблемы следует создать отказоустойчивую систему приводов механизмов параллельной кинематической структуры, позволяющей корректировать режим эксплуатации с учетом технического состояния. С этой целью необходимо определить текущую нагрузку на каждый исправный привод, а затем, зная количество и взаимное расположение неисправных приводов, рассчитать дополнительную нагрузку на каждый исправный.
Машиностроение и машиноведение
Материалы и методы. Надежное функционирование систем приводов механизмов параллельной кинематической структуры обеспечивается постоянным контролем и оценкой технического состояния каждого исполнительного элемента в режиме реального времени [1]. Для этого разработан высокоэффективный метод диагностирования, основанный на анализе тока электродвигателя с помощью вейвлет-преобразования [2]. Суть метода можно описать так: с учетом характерных масштабов рассчитываются значения вейвлет-коэффициентов тока электродвигателя, затем строится огибающая и рассчитывается ее аппроксимирующая прямая. Анализ коэффициентов k и b полученной прямой позволяет определить текущее техническое состояние привода. Если для всех характерных масштабов к < 0, то привод исправен, если к > 0 — неисправен. Таким образом, зная знаки коэффициентов k аппроксимирующих прямых, можно определить текущее состояние каждого привода, рассчитать количество и расположение неисправных приводов относительно друг друга [3].
Для последующей корректировки режима эксплуатации механизма параллельной кинематической структуры необходимо определить текущую и дополнительную нагрузки на каждый привод системы. Расчет текущей нагрузки на привод основывается на анализе всех параметров аппроксимирующей прямой для заведомо исправного ненагруженного электропривода, работающего в номинальном режиме. Полученные данные являются эталонными коэффициентами k0,b0, с которыми сравниваются текущие значения параметров k, b . Значение максимально допустимых коэффициентов kmax,bmax можно рассчитать по перегрузочной способности электродвигателя по току KT [4]. Тогда возможные изменения коэффициентов k, b вычисляются из соотношений:
∆ k =
k - k 0 k - k, max 0
∆ b =
b - b 0 b - b.
max 0
Для определения возможности повышения нагрузки на приводы системы разработана модель на базе аппарата нечеткой логики. Входы модели — относительные коэффициенты Δk, Δb (рис. 1), выход — соответствующий коэффициент, показывающий процент нагрузки на двигатель. Если данный параметр равен нулю, то привод работает в номинальном режиме без нагрузки. Если он равен 100 %, то двигатель имеет
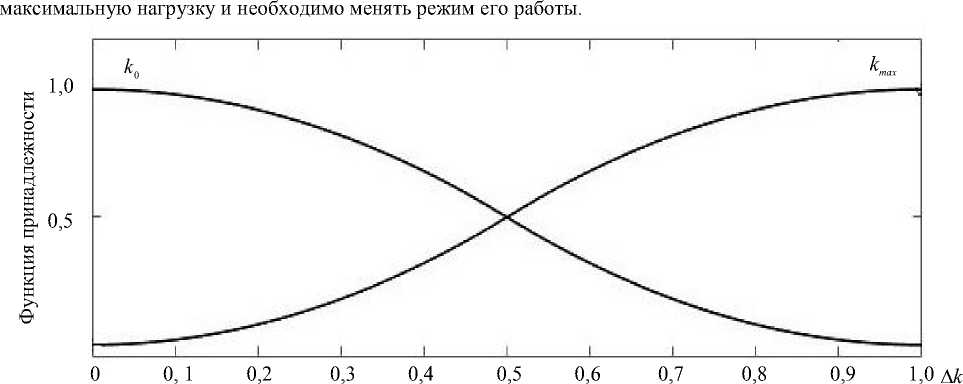
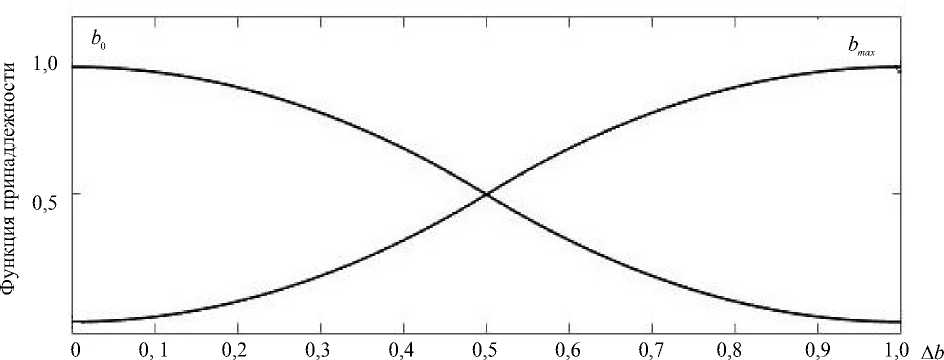
Рис. 1. Входные данные нечеткой модели определения нагрузки на электропривод
Корреляция введенных множеств может быть записана с помощью следующих нечетких правил: R 1: если k есть k 0 и b есть b0 , то Load ПД =l1;
R 2: если k есть k max и b есть bmax , то Load ПД =l2.
Для определения значения выходной переменной используется алгоритм нечеткого логического вывода Sugeno [5–14].
Предложенная модель позволяет по результатам анализа коэффициентов прямой, аппроксимирующей огибающую значений вейвлет-коэффициентов, определить текущую нагрузку на электропривод в процентах от предельно допустимой. В случае отказа одного или нескольких приводов системы и допустимой текущей нагрузки на исправные приводы возможна ко k0 рректировка режима эксплуатации и перераспределение высвободившейся нагрузки на исправные приводы. Для этого необходимо разработать модель расчета дополнительной нагрузки.
Рассмотрим решение данной задачи на примере платформы с двенадцатью параллельными стойками, каждая из которых представляет собой электромеханический домкрат. Равномерный подъем платформы обеспечивается синхронным, равномерным движением всех стоек с заданной скоростью. Для выполнения этого условия при проектировании механизмов параллельной кинематической структуры закладывается равность нагружения подъемных колонн. В этом случае при исправной работе механизма все приводы должны иметь примерно одинаковую внешнюю нагрузку
Ь^ ПД 1 ~ Load 2 ~ •••• ~ LoadПД,1 . (2)
При отказе одного из приводов перемещаемая им нагрузка перераспределяется на два соседних примерно в равных долях (рис. 2).
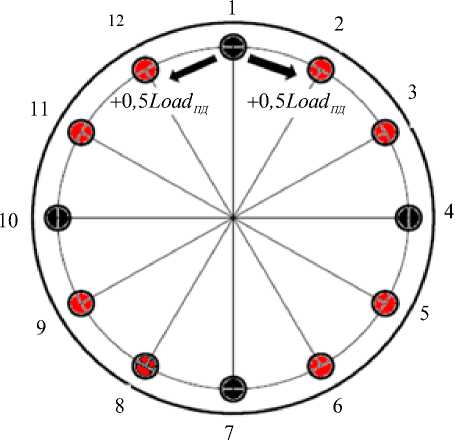
Рис. 2. Взаимное положение неисправных приводов домкратов и возможная коррекция нагрузки
+0,5 • Loadnn
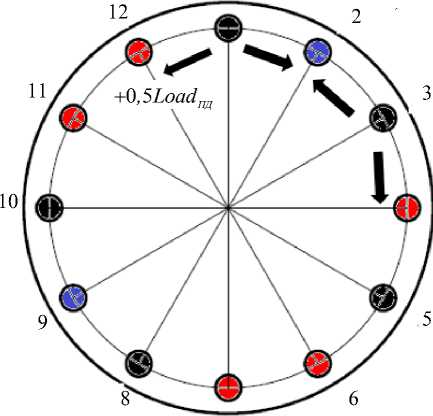
В данном случае дополнительная нагрузка рассчитывается из соотношения (3) и зависит от коэффициента изменения нагрузки ( Lch )
^ Load„„ = L. • Load„„ . (3) ПДj ch ПД i
Этот коэффициент зависит от количества и взаимного расположения неисправных приводов домкратов. Теоретически коэффициент изменяется в диапазоне от 0 до n с шагом 0,5. Коэффициент увеличения нагрузки является определяющим при расчете дополнительной нагрузки на привод механизма. Для его расчета разработана модель, основанная на применении аппарата нечеткой логики [7]. Входы модели — техническое состояние каждого привода механизма параллельной кинематической структуры, выходы — коэффициент изменения нагрузки на привод каждого домкрата. В результате диагностирования устанавливается текущее техническое состояние приводов: «исправен» или «неисправен». Поэтому для каждого входа системы на интервале [0 1] задаются Z - и S -образные функции принадлежности (рис. 3 а ). Исправному приводу будет соответствовать значение входа 1, неисправному — 0. Увеличение коэффициента роста нагрузки больше 2 приводит к критическим перегрузкам домкрата, поэтому в диапазоне L h е [ 0 , 2 ] задаем пять треугольных функций принадлежности с шагом 0,5 (рис. 3 б ).
Машиностроение и машиноведение
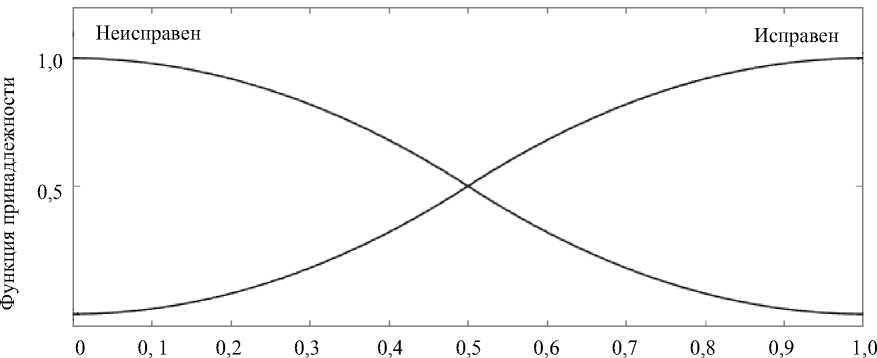
Техническое состояние двигателя
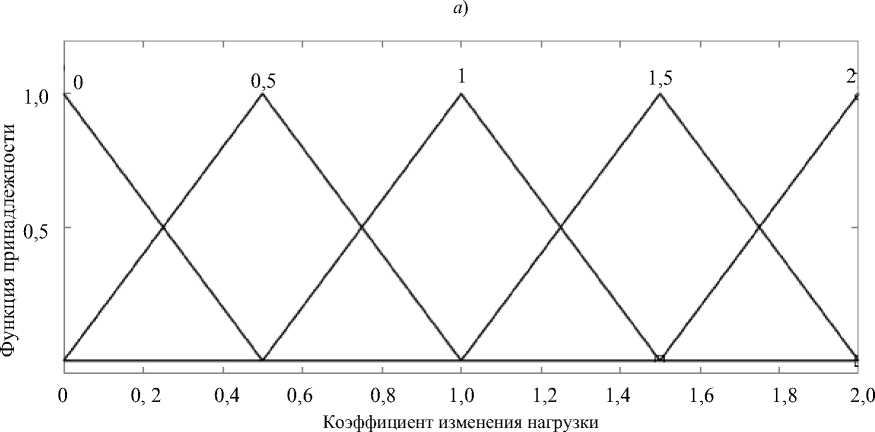
б )
Рис. 3. Функции принадлежности нечеткой модели расчета коэффициентов изменения нагрузки
Для расчета коэффициента увеличения нагрузки на электроприводы механизмов параллельной кинематической структуры использован алгоритм Mamdani [8–10]. Полученная модель основывается на анализе количества и взаимного расположения неисправных стоек механизма параллельной кинематической структуры. Эти данные позволяют определить коэффициент дополнительной нагрузки на каждый исправный привод.
Взаимосвязь между введенными множествами записывается в виде базы знаний, фрагмент которой приведен в таблице 1.
Таблица 1
Нечеткая база знаний модели расчета коэффициента дополнительной нагрузки
|
Номер домкрата |
Коэффициент изменения нагрузки домкрата |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
… |
n |
1 |
2 |
3 |
4 |
5 |
6 |
… |
n |
|
1 |
1 |
1 |
1 |
1 |
1 |
… |
… |
0 |
0 |
0 |
0 |
0 |
0 |
… |
… |
|
1 |
0 |
1 |
1 |
1 |
1 |
… |
… |
0,5 |
0 |
0,5 |
0 |
0 |
0 |
… |
… |
|
1 |
0 |
0 |
1 |
1 |
1 |
… |
… |
1 |
0 |
0 |
1 |
0 |
0 |
… |
… |
|
1 |
0 |
0 |
0 |
1 |
1 |
… |
… |
1,5 |
0 |
0 |
0 |
1,5 |
0 |
… |
… |
|
1 |
0 |
0 |
0 |
0 |
1 |
… |
… |
2 |
0 |
0 |
0 |
0 |
2 |
… |
… |
|
1 |
0 |
1 |
0 |
1 |
1 |
… |
… |
0,5 |
0 |
1 |
0 |
0,5 |
0 |
… |
… |
|
….. |
… |
… |
… |
… |
|||||||||||
Объединив две разработанные модели, получим общую модель определения текущей и дополнительной нагрузок на приводы механизма параллельной кинематической структуры (рис. 4).
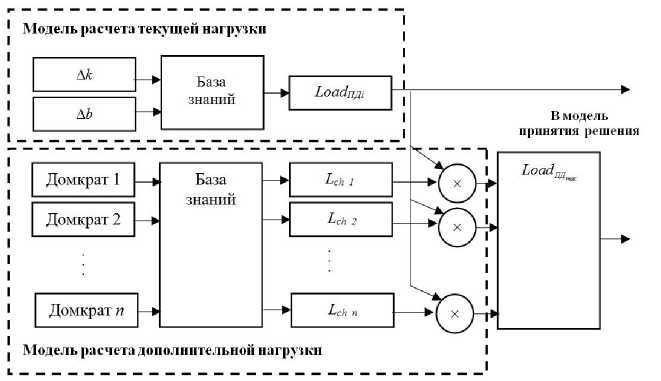
Рис. 4. Структура модели расчета текущей и дополнительной нагрузок на приводы механизма параллельной кинематической структуры
Приведенная модель базируется на количестве и взаимном расположении исправных приводов механизма параллельной кинематической структуры. При этом с учетом характерных масштабов анализируются относительные коэффициенты прямых, аппроксимирующих огибающие значений коэффициентов вейвлет-преобразования тока электродвигателей. Эти данные и аппарат нечеткой логики позволяют определить текущую и дополнительную нагрузку для обеспечения надежности электродвигателей.
Результаты исследования. Для проверки работоспособности предложенного метода расчета текущей и дополнительной нагрузки использовали стенд (рис. 5), состоящий из четырех электромеханических подъемных домкратов с приводом постоянного тока KY110AS0415-15B-Д2, синхронно перемещающих груз.
+ 0 , 5 Loadnn
+ 0 , 5 Loadnn
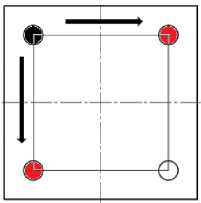
Рис. 5. Расположение неисправного домкрата и возможный вариант коррекции режима эксплуатации механизма параллельной кинематической структуры
Текущая нагрузка на приводы оценена по итогам анализа всех параметров прямой, аппроксимирующей огибающие коэффициентов вейвлет-преобразования с учетом характерных масштабов для заведомо исправного привода, работающего в номинальном режиме. В нашем случае речь идет о результатах первого замера токового сигнала приводов при их установке на электромеханические домкраты. Полученные данные использованы в качестве эталонных k 0 ,b 0. С ними сравниваются текущие значения измеряемых параметров k , b.
Для каждого масштаба вейвлет-коэффициентов рассчитаны относительные коэффициенты A k, A b, определена текущая нагрузка на каждый привод. Расчеты показали, что средняя нагрузка на все приводы примерно одинаковая — 29,52 % от максимальной. Задача эксперимента — проверка возможности перераспределения нагрузки на два соседних домкрата и исследование поведения системы в этом случае. Нагрузка, перемещаемая неисправным домкратом, перераспределяется на два соседних домкрата в равных долях — по 14,76 %. Тогда общая нагрузка на приводы 1 и 3 (рис. 5) — 44,28 %. Согласно нагрузочной диаграмме это безопасно для сервопривода. Нагрузка да привод четвертого домкрата остается неизменной — 29,52 %. Поскольку коэффициент k для всех приводов отрицателен, а их абсолютные значения значительно больше 0, то приводы имеют достаточный запас надежности.
Для определения влияния данного перераспределения нагрузки на техническое состояние приводов проанализированы механические и электромеханические характеристики сервоприводов. Установлено, что все три режима эксплуатации допустимы для исследуемого сервопривода. Они не ведут к динамическим перегрузкам и преждевременному отказу. Это позволяет обеспечить надежное функционирование комплекса
Машиностроение и машиноведение
при проведении ремонтных работ.
Обсуждение и заключения. Разработана модель оценки текущей и дополнительной нагрузки на электрические приводы механизмов параллельной кинематической структуры. Получаемые таким образом данные необходимы для коррекции режима эксплуатации системы приводов в случае отказа исполнительных элементов. Для расчета нагрузки использованы коэффициенты прямой, аппроксимирующей огибающую вейвлет-коэффициентов тока с учетом характерных масштабов. Кроме того, учитывается количество и взаимное положение неисправных домкратов относительно друг друга. Эксперименты показали адекватность представленных методов.
Список литературы Метод оценки текущей и дополнительной нагрузки на систему электрических приводов механизмов параллельной кинематической структуры
- Альван, Х. М. Декомпозиция задачи силового анализа многоподвижного механизма параллельной структуры / Х. М. Альван, А. В. Слоущ // Теория механизмов и машин. — 2005. — Т. 3, № 1. — С. 35-39.
- Круглова, Т.Н. Исследование технического состояния электропривода при различных условиях нагружения / Т. Н. Круглова // Вестник БГТУ им. В. Г. Шухова. — 2019. — № 3. — С. 112-113.
- Булгаков, А. Г. Диагностирование технического состояния электропривода на основе применения вейвлет-преобразования / А. Г. Булгаков, Т. Н. Круглова // Бюллетень строительной техники. — 2019. — № 8 (1020). — С. 46-50.
- Aksenov, Y. On line PD Diagnostic on Medium Voltage Motors and Cable Lines: Useful Tool for the Maintenance Manager / Y. Aksenov, I. Arces, G. Noe // IEEE — URL : https://ieeexplore.ieee.org/document/1380497 (accessed: 24.08.2021). 10.1109/ELINSL.2004.1380497
- Isermann, R. Fault-Diagnosis Applications. Model-Based conditions monitoring: Actuators, drives, plants, sensors and fault-tolerant systems / Rolf Isermann. — Berlin : Springer, 2011. — 466 p.
- Cruz, S. M. A. Rotor cage fault diagnosis in three-phases induction motors by extended Park's Vector Approach / S. M. A. Cruz, A. J. M. Cardoso // Electric Machines & Power Systems. — 2000. — Vol. 28 (4). — P. 289-299.
- Гаскаров, Д. В. Искусственные информационные системы / Д. В. Гаскаров. — Москва : Высшая школа. — 2003. — 435 с.
- Заде, Л. А. Понятие лингвистической переменной, его применение к принятию приближенных решений / Л. А. Заде. — Москва : Мир, 1976. — 77 с.
- Круглов, В. В. Искусственные нейронные сети. Теория и практика / В. В. Круглов, В. В. Борисов. — Москва : Телеком, 2002. — 382 с.
- Noninvasive detection of broken rotor bars in operating induction motors / G. B. Kliman, R. A. Koegl, J. Stein [et al.] // IEEE Transactions on Energy Conversion. — 1988. — Vol. 3 (4). — Р. 873-879. 10.1109/60.9364
- Jee-Hoon Jung. Online Diagnosis of Induction Motors Using MCSA / Jee-Hoon Jung, Jong-Jae Lee, Bong-Hwan Kwon // IEEE Transactions on Industrial Electronics. — 2006. — Vol. 53 (6). — P. 1842-1852. 10.1109/TIE.2006.885131
- Investigation of torque security problems in electrified vehicles / Jiyu Zhang, Alessandro Amodio, Bilin Aksun Guvenc [et al.] // In: Proc. ASME 2015 Dynamic Systems and Control Conference. — URL : www.researchgate.net/publication/281295777 DSCC2015-9627 investigation of torque security problems in electrified vehicles (accessed: 24.08.2021). 10.1115/DSCC2015-9627-9627
- Jiyu Zhang. Fault diagnosis for electric drive systems of electrified vehicles based on structural analysis / Jiyu Zhang, Hongyang Yao, Giorgio Rizzoni // IEEE Transactions on Vehicular Technology. — 2016. — Vol. 66 (2). — P. 1027-1039. — URL : https://www.researchgate.net/publication/301571844 Fault Diagnosis for Electric Drive Systems of Electrified Vehicles Based on Structural Analysis (accessed: 24.08.2021). 10.1109/TVT.2016.2556691
- Thomson, W. T. Current signature analysis to detect induction motor faults / W. T. Thomson, M. Fenger // IEEE Industry Applications Magazine. — 2001. — Vol. 7 (4). — P. 26-34. 10.1109/2943.930988
