Метод оценки вероятностей состояний специальной системы массового обслуживания

Предлагаетсяметодрешения системыуравнений, позволяющий точно определять вероятности состояний системы массового обслуживания.

В статье [1] предложен метод вычисления характеристик замкнутой системы массового обслуживания (СМО) с ожиданием и случайным распределением заявок по всем каналам обслуживания без взаимодействия между собой, имеющей большое прикладное значение, например, для оценки производительности многопроцессорных вычислительных систем. Данный метод основан на решении системы уравнений численным методом, что предполагает использование большого объема оперативной памяти ЭВМ и занимает значительное время при реализации алгоритмов решения системы уравнений. Приведенная в указанной работе обобщенная формула для определения вероятностей состояний СМО позволяет ускорить исследования, но вероятности по этой формуле вычисляются с определенной ошибкой по отношению к решению системы уравнений численным методом.

В данной статье рассматривается замкнутая система с ожиданием и равновероятным распределением заявок от т источников, идентичных по всем п каналам без взаимодействия между собой [2]. При этом предполагается, что суммарный поток заявок на обслуживание подчиняется пуассоновскому закону распределения с параметром V , а время обслуживания каждым каналом - экспоненциальному закону распределения с параметром ц . Вновь поступившая на обслуживание заявка направляется с равной вероятностью в любой из свободных каналов и принимается на обслуживание. Если же все шины заняты, то поступившая на обслуживание заявка становится в очередь и ждет своего обслуживания. Обслуживание заявок из очереди осуществляется в порядке поступления.

Для идентификации рассматриваемой СМО можно использовать стандартные обозначения Д. Г. Кендалла (1953) в форме а / Ъ / с , дополненные А. М. Ли (1966) обозначениями d и I и расширенные в [3] обозначением / Однако принятая идентификация не отражает способ организации распределения поступивших заявок по каналам обслуживания, т. е. того, в какой канал направляется вновь поступившая заявка: в первый освободившийся или в любой другой с какой-либо вероятностью, например 1/ п . Для более полной идентификации СМО введен дополнительный символ g , указывающий порядок выбора канала обслуживания. С целью конкретизации порядка выбора канала обслуживания примем следующие обозначения:/- при выборе первого освободившегося канала; а - при выборе с определенным заказом любого канала. Для обозначений выбраны первые буквы английских слов/гее - свободный и апу - любой, всякий.

Таким образом, исследуемая СМО с помощью известных [3] и дополнительных обозначений идентифицируется следующим образом:

( M / M / n ) : | ПЕРППО / m / m / —

I                  n

Система линейных уравнений рассматриваемой СМО при п >  т для стационарного режима имеет следующий вид[1]:

^т Р ^РР 1.0 ,

[( m ^{- — -} 1) р + ^— ] Ру = ( m ^- k ^- I + 1)р n ^{k + 1} P _ ! । + n ⁽¹⁾

l

+ (m - — -1 + 1)р-Pk, t-1 +          P—+1, t + n          (— I 1)

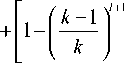
—P-, t+1, mPm ,0

= P n - m +1

Pm-1,0 , n где Рк , - вероятность нахождения СМО в состоянии, при котором к заявок находятся в очередях и ждут своего обслуживания; р = V / ц; — = 0, m ; 1 = 0, m - —.

При решении системы уравнений (1) для СМО, состоящей из двух источников заявок ( т = 2), и равном или больше двух каналов обслуживания ( п >  2) определим выражения для вероятности состояний Р ,, ( п = 1,2; / = 0,1) с точностью до Р _{0 0} Последовательно увеличивая на единицу число источников заявок т при п >  т и решив систему уравнений (1), получаем, что выражения для вероятностей Р_{к 1}( — = 1, m и 1 =0, m - — ) совпадают, следовательно необходимо определить выражения только для вероятностей P_{k m}__{k+ i} и P _m+i0 ( / =1,2,...) дополнительных состояний, получаемых за счет увеличения числа источников заявок и каналов. Совпадение выражений для определения вероятностей основано на отсутствии последействия пуассоновского закона распределения потока событий.

В результате последовательного решения системы уравнений (1) при п >  т + / ( / = 1, 2, ...) получим новую систему уравнений для определения вероятностей Р : ^к . I

Р 1,0= т рР0,0, m - — -1 +1 n - — +1 „

-------;-------Р----------P— -1, t + kn

^ —р р 1 —, 1 -1

J n

m - — - 1 + 1 k

Р ₌ 1 р ^{n - m + 1} р

¹ m ,0         ^{р               1} m - 1,0 .

mn

Таким образом, для определения вероятностей Р _к/ достаточно решить систему уравнений (2), последовательно выражая вероятности Р _1рР _к1 ,Р _т0 через Р _{0 0} .

Сделав соответствующие преобразования по схеме, реализующей метод индукции, получим решение в об-

Математика, механика, информатика

щем виде. Используя условие нормировки [1], определим выражение, позволяющее определить вероятности Р состояний СМО:

( k + 1 -1Y n )

m !        1

P_k , 1 =

i "1 P+j-1

P

J^ k J ( m - k - 1 ) ! n ^{( k + 1} )

⁽ k + 1 )

n ^

m !        1

i , ( m - i - j ) ! n ⁽ ' ⁺ j ) P

—, (3)

, ( i + j )

I n при m >  n , где h = < [ m при m <  n .

Для определения функциональных возможностей СМО найдем их основные характеристики, к которым относятся среднее число заявок, ожидающих обслуживания в очередях (средняя длина очереди) l , среднее число обслуживаемых одновременно заявок l _о6сл , среднее число простаиваемых источников заявок l _пр , коэффициент использования источников заявок £ , коэффициент простоя источников заявок у , вероятность занятости канала Р _зк и вероятность того, что все каналы заняты Р _{п з} [2].

Среднее число заявок, ожидающих обслуживания, определяется как математическое ожидание длины очереди в системе [1] и равно сумме произведений вероятности P_fcl на количество заявок l , ожидающих обслуживания в соответствующем состоянии, по всем состояниям, в которых значение ожидающих обслуживания заявок не равно нулю.

Среднее число обслуживаемых заявок - это сумма произведений вероятности Р ^ _; на число одновременно обслуживаемых заявок к по всем состояниям СМО, в которых количество обслуживаемых заявок не равно нулю.

Среднее число простаиваемых источников заявок определяется как сумма среднего числа обслуживаемых заявок и среднего числа ожидающих обслуживания заявок, так как источник заявок простаивает во время ожидания и обслуживания.

Коэффициент простоя источников заявок равен частному от деления числа простаиваемых источников заявок на общее число m источников заявок.

Коэффициент использования источников заявок представляет собой вероятность того, что определенный источник заявок в любой момент времени будет работать, и равен как разности между полной вероятностью состо

яний СМО, т. е. единицей и коэффициентом простоя источников заявок.

Для определения оптимального количества каналов в СМО необходимо найти вероятность занятости канала, которая равна отношению среднего числа обслуживаемых заявок к числу каналов.

Вероятность того, что система полностью загружена, определяется как вероятность того, что в системе все каналы заняты. Она является суммой вероятностей P_{h ;} состояний СМО, в которых число одновременно обслуживаемых заявок равно количеству каналов, если количество каналов не больше количества источников заявок, или количеству источников заявок в противном случае.

Зная характеристики СМО, можно определить область ее использования, причем те или иные ее характеристики могут быть использованы в различных практических приложениях.

Таким образом, предложен метод оценки характеристик специальной системы массового обслуживания, которая может использоваться для моделирования функционирования ряда технических систем, в том числе многопроцессорных вычислительных систем при обращении микропроцессоров к общей памяти. В общем виде получено выражение для решения системы линейных уравнений, описывающей поведение СМО в стационарном режиме. При расчете производительности по методике, изложенной в [1], относительная ошибка практически равна нулю.