Метод оценок интервальных распределений простых чисел

Основываясь на теореме о полном множестве простых чисел, доказательство которой приведено в данном сборнике в статье В.А. Минаева, в настоящей работе описываются результаты, свя занные с:

• •    моделированием эффекта «пересечений» аддитивных последовательностей, формирующих составные числа { 6 n ± 1 } , n = 1, 2, 3, ... ;

• •    обоснованием нового метода интервальных

оценок распределения простых чисел;

• •    доказательством гипотезы Лежандра, гипотезы Брокарда, гипотезы «простых близнецов».

В теореме о полном множестве простых чисел вида доказано, что уравнения, описывающие механизм формирования составных чисел вида {6 к ± 1}, к = 1, 2, 3, ... и дающие возможность однозначно выделить все простые числа из множеств {6 к ± 1}, к = 1, 2, 3, ... [1-5, 7, 9], представляются следующим образом:

c+- pi c+t

Pi c\ pi c.

^Pi ⁺

= P i ^- Pi + P i ^{- 6} m = P t " Pi + Р* - ⁶ m = P i - P ^{t +} P i - ⁶ m = P + ^- P i ⁺ P i^{- 6} m ;

m = 0, 1, 2, 3,    ; i = 1, 2, 3, ... , где введены следующие обозначения:

• •    pi , i = 1, 2, 3, ... - простое число из множества { 6 к - 1 } , к = 1, 2, 3, ... с недостающей единицей для деления нацело на 6 (минус простое число - МПЧ);

• •    pi , i = 1, 2, 3, ... - простое число из множества { 6 к + 1 } , к = 1, 2, 3, ... с избыточной единицей для деления нацело на 6 (плюс простое число - ППЧ).

Соответственно, c i - минус составное число (МСЧ) из множества { 6 к - 1 } , к = 1, 2, 3, ... с недостающей единицей для деления нацело на 6; а c i - плюс составное число (ПСЧ) из множества { 6 к + 1 } , к = 1, 2, 3, ... с избыточной единицей для деления нацело на 6 (ПСЧ).

Понятия МПЧ, ППЧ, МСЧ и ПСЧ впервые введены в работах [6, 8].

Как показано при доказательстве теоремы о полном множестве простых чисел, без ограничения общности в соотношениях (1) р ⁺ и p i можно заменить на q i и q i , обозначающие два ряда проиндексированных натуральных чисел из множеств { 6 к + 1 } и { 6 к - 1 } , к = 1, 2, 3, ...

• c i = qi- qi + qi- 6 m q _i

• c t = qi- qi ■ qi • 6 m

q i

• ci- = qi- qi + qi • 6 m

q _i

• ^с - + = qi • qi⁺ qi- 6 m ; q _i

  
  

m = 0, 1, 2, 3, . ; i = 1, 2, 3, . .

Очевидно:

{q.—}={ p"}u C};{q.+}={ p*} и {C/}-

Подставляя значения m и m ⁺ из (5) - (8), имеем:

max

C ( n ) = E 1

. = 1

^{n -} q .

6 qi • £ ⁺ _q

6 q i

^{n —} q .^{2 — 6} q .' ■ ^£_q +

6 q i

+

Использование q вместо p в соотношениях (2) значительно ускоряет процедуру нахождения простых чисел и упрощает различные оценочные операции в связи с тем, что разница меж-

^{n —} q — • q . ⁺

6 q: • £

6 q .

,+

ду стоящими друг против друга q и q всегда равна 2.

Интервальные оценки распределения простых чисел

Применяя уравнения (2), определим количе-

ство МСЧ и ПСЧ, образуемых каждым на интервале (0, n ).

Из первого уравнения (2) следует:

q^2 + qf • 6m + q— • 6e + — n = 0.

q

q

^и q. ⁺

^{n —} q . ⁺ • q . ^{— — 6} q .' ■ ^£ _q — +

⁶ q i

+ 4 [ . (12)

Используя обозначение q. = q. и q. ⁺ = q. + 2, получаем:

max

C ( n ) = E i = 1

+

6 q i

Откуда

m ⁺

—2 n — q .

6 q, • £ ⁺ q

6 q ^-

где m ⁺ ( q. ^— , n ) - число ПСЧ, образуемых арифметической прогрессией, формируемой первым уравнением (2); единица добавляется для учета первого члена прогрессии.

Аналогично из второго уравнения (2) имеем:

m ⁺

из третьего –

m (q. , n

и четвертого –

m

n -

q . ^{+ 2}

6 q.⁺ - <+

⁶ q . ⁺

n

, +

q . • q .

6q

⁶ q ^- • £

n

- ⁶ q .

q

n

J L 6 ( q + ² )

ql+l _F+

6           ^q.¹

+

n   qi + 2

— £

n

qi

6 ( q . I 2 ) 6

Введем обозначение: M = . max.

+ 41

Примем, что математическое ожидание сред-

него значения ошибок £+ q да сумма всех £q равна: M

V £ ± = q

I=1

£ ++ q

M

= £

q

+

+ « £ + q .

тог- 2^,

.

Выражение в фигурных скобках приобретает следующий вид:

M

C (n ) = Z i=1

или

n

n

q

3 q .   3 ( q .+ 2 ) 6

— 2 M + 4 M , (15)

M

E ² q . i 2 M — 2 M .    ⁽¹⁶⁾

i = 1 ^{3                3}

Подставляя в (16) значение q. = 6 i - 1 и учи-

тывая, что

M

E =

I=1

M (M +1)

,

n — q.'• q——6 q.'•£—+

q

⁶ q.⁺

получаем

M

C ( n ) = n УI -⁽ ) 3 1: 1 ( q —

Проделав имеем

) M

— I — £2 ( 6 . — 1 ) + 2 M-MM . (18) q j t13^v '       3

соответствующие вычисления,

В соотношениях (4) – (8) по определению

n

k =2 M

C (n ) = 7 E - — 2 M

³     . = 1 si

.=1 s.

2

q

Из (5) – (8) вытекает, что общее количество МСЧ и ПСЧ вида { 6 k ± 1 } , k = 1, 2, 3, .„ , образу-

или учитывая, что при n >>  1 M = V n /6, как показано в статье Минаева В.А. в настоящем

емых на интервале (0, n ), равно:

C ( n ) = C ⁺ ( n ) + C ^— ( n ) ,

сборнике,

где

C ^— ( n ) = E { m ^— ( q. ^— , n ) + m i = 1 ¹

(q.+, n)}

C ⁺ ( n ) = £ { m ⁺ (q, ^— , n ) + m ⁺ i = 1 ¹

в которых _max равно индексу максимального q , участвующего в формировании ПСЧ и МСЧ на интервале (0, n ).

ⁿ ( 2 M ^{1   1}

C(n)=3 L?-7

3 .=1 s.     6

.=1 s.

6 /

где s. - число вида 6. ± 1; . = 1, 2, ... 2 M .

С учетом того, что ПСЧ и МСЧ, образуемые в (2) от соответствующих ПСЧ и МСЧ, повторяют ПСЧ и МСЧ, формируемые изначально от минус и плюс простых чисел, устраним «эффект дублирования», записав выражение (20) в виде:

ⁿ f ^{1 1 1}

C1(n) = ^ -л, 3 y=1 p 6)

где L - максимального простого числа, участвующего в образовании составных чисел на интервале (О, n ), { p } = { p - } U { P ^j } .

Как показано в работах [11, 12], существует эффект «пересечений» аддитивных последовательностей, формирующих составные числа, который также необходимо учесть в (21). В работе [12] приведены соотношения, с помощью которых формируются «пересечения» для ПСЧ:

Определим А ₁ для МСЧ и ПСЧ как:

^A- ( q - , qj ) = ⁶ qj- qi

A-( qj, qj) =6 qj- qj

^A- ( q j , qj ) = ⁶ q j^- qj

A-( qj, qj) =6 qj- qj

- E i, q

- E j j q z , q

- E j q _i

, q j

- E j j q z , q ,

qi • qi + qi • 6 m = qj • qj + qj • 6l qi • qi + qi • 6 m = qi • qj + qj • 6 l qi • qij qi • 6 m = qi • qij qj • 6 l qi • qi■ qi • 6 m = qj • qj■ qj • 6 l;

где z , j = 1, 2, 3, ... , M ; m , l = 0, 1, 2, ... .

^{A j} ( q j , qj ) = ⁶ q j^- qj ^{A j} ( q j , qj ) = ⁶ q j^- qj ^{A j} ( q j , qj ) = ⁶ q j^- qj A j ( q j , qj ) = 6 q j - qj

-

E ^j _

+

qj, qj

-

E

,+

+

qz ,qj

-

E

.+

qj, qj

-

E

,+

+

+

qz ,q,

,

Вторая система уравнений, определяющих

«пересечения» МСЧ, записывается в виде: qi • qi + qi • 6 m = qi • qi + qj • 6 ⁶ qi • qi + qi • 6 m = qj • qj + qj • 6 ⁶ qi • qi + qi • 6 m = q i • qj + qj • 6 ⁶ qi • qi ■ qi • 6 m = qj • qj ■ qj • 6 ⁶ ;

где z , j = 1, 2, 3, ... , M ; m , l = 0, 1, 2, ... .

Нетрудно показать, что для общего случая

период, через который в последовательностях

возникают «пересечения», равен:

T ( q, , q, ) = 6 - q • q ; z , j = 1, 2, 3, .... (24)

При этом каждому m в уравнениях (22) и (23) соответствует свое l , при которых правая и левая часть уравнений совпадают.

Учитывая (22) и (24), представим уравнения для нахождения количества «пересечений» ПСЧ

где 0 <  e ±    <  1.

qz ,q

Третий член уравнений (25) и (26) отражает последующие «пересечения» арифметических прогрессий.

Четвертый член равен разности между n и последним «пересечением» арифметических прогрессий, образуемых парой ( q_z , q₃ ) , ( i ^ j ) . Он равен A ± ( q ± , qj ) = 6 q ± - q ^±- 5 ^±± ± , при этом 0 <  5 ± ±± < 1.     '              '    ' q ' ^,4‘

q i, q j

Учитывая введенные определения, запишем первое уравнение из (26) в виде:

qi2 j 6qj- qj - EH- я- j 6qj- qj • k j J       qi ,qj j 6qj - qj - 5j_ j = n. z j        qz, qj

в виде:

Из (29) имеем:

k j( q^j ,q j

q^ ² +A j ( qi , qj ) + 6qi • qj • k +A j ( qi , qj ) = n q^ ² + a ^j ( q^ , q j ) + 6 q^ • q j * k + A ^j ( qi , q j ) = n qi² + A j ( q i , qj ) + 6 q i • q j • k j A j ( q j, q j ) = n q ⁺ + A j ( q j, q j ) + 6 q j • q j • k + A j ( q j , q j ) = n ,

n - q,¹ - 6 q, - q - e ^j _ ^{z              z} j       q z , q

^{j 6} qi - q j ^- 5 j i

' j , qj

где z , j = 1, 2, 3, ... ; k = 0, 1, 2, 3, ... .

⁶ qz ^- q j

(29) ^j 1,

где K ⁺( q_z , q ) - количество «пересечений» избранной пары арифметических прогрессий на

И, соответственно, для МСЧ с учетом «пересечений» запишем:

отрезке (0, n ).

Упрощая выражение (29), получаем:

qi • qi + А[ (qi, qj) + 6 qi • qj- к + A - (qi, qj ) = n qi• qi+ Ai(qi,qj)+6qi• qj-k+A2(qi,qj) =n (26) qi • qi + Ai (qi, qj) +6 qj • qj- k+A i (qi, qj) = n qj • qi i a- (qj, qi) i 6qj • qi • k i Aj (qi, qi ) = n, где z, j = 1, 2, 3, _ ; k = 0, 1, 2, 3, _ .

Отметим, что в уравнениях (25) и (26) сумма

K •(

n

⁶ qi- q j

qi

6 q.

E j z - 5 j j j 1.(30) q , q      q , q ,

Проделывая те же операции (28) - (30) для

других уравнений (25) и суммируя по всем возможным сочетаниям q,,q₃ ( i ^ j ) , получим общее количество «пересечений» для ПСЧ:

первых двух членов равна составному числу -первому «пересечению» арифметических прогрессий, формирующих МСЧ и ПСЧ с помощью (22) и (23). Второй член А - ( q_z , qj ) и A j ( q_z , qj ) равен длине отрезка в арифметической прогрессии, через который образуется первое «пересечение» последовательностей, формируемых числами q_z и qj ( z ^ j ) вида { 6 m ± 1 } , m = 1, 2, 3, ... .

K ^j

M

= 2

*, j =1

* * j

n v6qj ■ q -

n j--

6 q j - q ^j

M _q/_i_qj_ 2,1 6 q - 6 q j i * j v J          J

j-----rj

6 q j - q.

j - j q z    , q z

6 q ^-    6 q ^j ^

n

6 q j - q ^j

-     (31)

MMM

- 4У e ± ± ± - 4У 5 ± ± ± j 4У1.

q , q,          ( 4 q , q,          < 4

z , J = 1      ' ^J          z , J = 1       ' ^J          z , J = 1

z * J                  z * J                  z * J

Выражение в первых скобках приводится к

виду:

M

L l, j=1 i * j

n

n

n

n

6 qi • q.     6 q" + • q⁺     6 qi • q.

⁶ qi • q ⁺

Подставляя в (36) значение M = n/ /6, получаем:

c 2 ( n ) =

= n у = 6 ^L . 1 q

I * j

q +

•

q -

q"

n

+ —

nn	n	n
— z--z	+ —	p --+
36	6	18
n	2	n
- z +-- z		.
66	3	6

n 2 M 1

2 M 1

n 2 M 1

n 1       1 n 1

6^=1 si jr1 Sj   61=1 s²’

Таким образом, количество простых вида { 6 k ± 1 } , k = 1, 2, 3, ... на интервале (0, n ) равно:

где { si } = { q . } ^ { q + } , объединенное множество, включающее 2 M элементов.

Второй член уравнения (32) отражает «самопересечения» арифметических прогрессий.

Во второй скобке (31) выражение приводит-

или

ся к виду:

M

^П ( n ) = n ^- c 2 ( n )

nn  n2

n (n ) =---z +—z

33  66

nn   nn

+zz +. 18 36    69

Группируя слагаемые в (39), получаем:

, +

, +

L   qi ₊ qi ₊ qi ₊ qi

,j11 6 q -   6 q +   6 q -   6 q+ i * j j             j             j             j -

6 q + 6 q_    6 q

n ( n ) = n ( 1 - z ) ² + ( 1 - p ) + 1 1 1 - z ]+    | 2 - z | . (40)

6                    3 V    2 J V n V 3 J

При n >> 1

1 ^M

= 1У q

6 ^L I  '

i * j ^L

i

+

— + — + q

-     z»⁺         i

q

q

q"

q _j

1 M 1    1 / -

-У +— ( q ⁺ q ) .

⁶ i , j = 1 1 q,    q,v         ’

* i

l * j

Чтобы упростить это выражение, подставим значения для q - = 6 i - 1 и q ⁺ = 6 i + 1, получив:

1 V 1    1

7 L —+— ( q, ⁺ q,) =

⁶., j 4 q, q,)

i * j         ^{j j}

2 M

= M ( M + 1 ) L M , z = 1 si     ³

где второй член также отражает учет неравенства i * j .

Наконец, вычисляя остаток выражения (31), получаем нулевое значение.

2 M 1

Обозначив выражение L — = z, получим co z' =1 si отношение для количества «пересечений» ПСЧ на интервале (0, n):

K ⁺ = nz 2 _ n p _ _M ( _M + 1 ) z + 2 _M , (34) 66      3

2 M 1 где p = L —. i = 1 s.

i

Нетрудно показать, что количество «пересечений» МСЧ описывается той же формулой (34). С учетом того, что во внимание нужно принять половину «пересечений», общее количество составных чисел на интервале (0, n ), с учетом «пересечений», описывается соотношением:

c 2 ( n ) =

nnn

— z----z +

n          , x 2

+ - p + M ( M + 1 ) z —M .

n ( n )

z

. (41)

Легко показать, что выражение в квадратных скобках (41) всегда больше нуля. Это означает, что n ( n ) всегда больше нуля, и п ( n ) ^да при n ^да .

На самом деле, выражение в квадратных скобках имеет вид:

I 2 13 ^4

F = z--z + —

V 6     3

Корни выражения в первых круглых скобках

равны:

13 , 1 13 V 4 z l =±л!

^1,2 12 К12 J 3

= 112 ( 13 ± 723 j ) , (43)

где j – мнимая единица.

То есть корни (43) мнимые, и всегда больше нуля.

Очевидно, что

1 - p = 1 - L

+ L

z

13    4

—z + —

M

= 1 —У-.

36 ^L i²

Ы            M 1 x n ²

Известно, что ^— при M ^да . tl i ²     6

То есть при M ^ да

1 - p ^ 1 - — = 0,908....

Так же как и в (21), чтобы устранить «эффект дублирования», выражение (41) представим в

виде:

^{n ( n} ) = n ^{( 1 - z ,)2 + ( 1 -} p ^{,)+ 1} 1 ¹ 6                       3 <

z'

, (46)

L 1            L 1

где z = ^ ; р = ^ 2; р . - простые числа, i=1 р,             i=1 р, участвующие в формировании составных чисел вида {6к ± 1}, к = 1, 2, 3, ... на интервале (0, n).

Выражение для ρ ′ представимо в виде:

Введем обозначения:   2

G (z ) = 1 - z + \ - р = =2 [(1 - z )2+(1 - р)].

р=ZP(2)-1 - 9

где Z p ( 2 ) — дзета-функция Римана на множестве простых чисел.

Известно [13], что

Очевидно, что n +1)2     , . 2(n +1)2

п [ ( n + 1)^!       3 ' - G ( z ) + -46-)-

( n + 1 ) 2     n + 1    2 n + 1

- ---- —z--z +---

36       6     3   6

^^^^^^B

Z p ( 2 ) ^ 0,453... при L ^^ . Соответственно, при L ^ да : р^ 0,092,

1 - р^ 0,908.

Используя определение дзета-функций Римана на множестве простых чисел, представим

(46) в виде:

1 - z ( 1 ) + ¹ + ¹ 1 + ^pV ’ 2 3 )

+ 1 1 - Z_D ( 2 ) + ¹ + ¹ | + ¹ 1

I ^ppV ) 4 9 I 3

^^^^^^^

^+ 1 + 1 ¹

2     4 6 I

или

2

n( n )= - [(L833-..-Zp (1)) +

⁺ ( 1,³⁶1... - Z p ( 2 ) ) + -( 2,⁸³³... - Z p ( 1 ) ) .

Доказательство интервальных гипотез

Доказательство гипотезы Лежандра

Гипотеза Лежандра (третья проблема Ландау) утверждает, что между n ² и ( n + 1 ) всегда найдется простое число. Докажем ее, опираясь на соотношение (39):

( \ - A , Z2 n( n ) = — 1 - z + — v ’ 3           2

Р ^^^^^^™ ^^^^^^^^^^^^

+

+ 2 M ² - M ( M + 1 ) - z + - M .

п [(n) ] = у- G(z)

2 n ²

+--

-

n ² z

-

n2n z + -- . (55)

n

Нетрудно показать, что G ( z ) и z образуются одними и теми же простыми числами, максимальное из которых не превышает n + 1. Вычитая (55) из (54), получаем количество простых чисел между n и ( n + 1 ) :

AnL = п [(n +1)2 ]-п [(n )2 ] =

^n3+I G (z) +

2 n + 1

-

2 n + 1     z 1

-----z --+ = (56)

36     6 9

2 n 3 +l G ( z )

+ +---- z 9636

nz

или

AnL «n3 (1 -z)2 +(1 -Р) + 311 -^21. (57)

Выражение в квадратных скобках аналогич-

но такому же выражению в (41), применительно к которому мы показали, что оно всегда больше 0. Таким образом, третья проблема Ландау реше-

на, и гипотеза Лежандра доказана.

На рисунке 1 приведена модельная (сплошная линия) и эмпирическая зависимость (кружки) количества простых чисел в интервале ( n ², ( n + 1)²) от количества простых чисел в интервале (0, n ), формирующих МСЧ и ПСЧ в интервале (0, ( n + 1)²). Очевидно хорошее согласование данных с коэффициентом корреляции, равном 0,996.

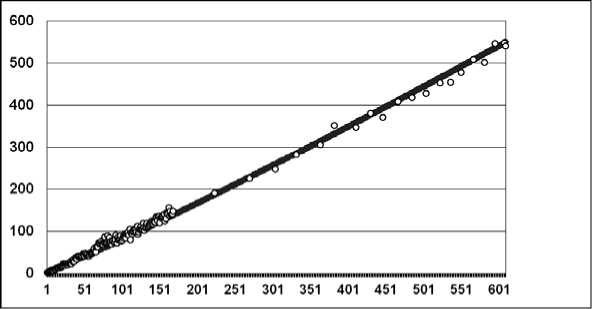
Рис. 1. Моделирование распределения простых чисел в интервале ( n ² , ( n + 1)²)

Доказательство гипотезы Бертрана

В 1845 году французским математиком Ж. Бертраном была выдвинута гипотеза, названная впоследствии постулатом, о том, что для любого натурального n >  1 найдется простое число в интервале ( n , 2 n ). В 1845 году эта гипотеза доказана русским математиком П.Л. Чебышёвым в его знаменитой теореме. Индийский математик С. Раманаджан в 1920 году нашёл более простое доказательство гипотезы Бертрана, а венгр П. Эрдёш в 1932 году – ещё более простое.

Используя доказательство теоремы Ландау, можно весьма просто обосновать справедливость постулата Бертрана.

Пусть m = 7й и m +1 = П+ +1.       (58)

Тогда

( m + 1) 2 - m ² = n + 2V n + 1 - n = 2 4n + 1. (59)

Покажем, при каких n справедливо соотношение:

2 V n + 1 <  n ,              (60)

означающее, что интервал, используемый в постулате, шире и включает интервал между квадратами последовательных чисел натурального ряда в решенной в настоящей работе проблеме Ландау, всегда содержащий простое число.

Из (60) следует

0 <  n ² - 6 n + 1 = ( n - 3 + 2V2 )( n - 3 - 2V2 ) . (61)

Анализ (61) показывает, что постулат Бертрана всегда справедлив при n >  5. Дополнительный анализ при 1 <  n <  5 свидетельствует о том, что названный постулат выполняется для всех n >  1.

Доказательство гипотезы Брокарда

Из доказательства гипотезы Лежандра лег- ко выводится утверждение, названное гипотезой Брокарда: между квадратами подряд идущих простых чисел, за исключением первых двух, всегда найдется хотя бы четыре простых числа.

Обозначим п ( р 2 _{+ 1} ) число простых чисел на интервале ( 0, р 2 _{+ 1} ) и п ( р^ ) - число простых чисел на интервале ( 0, р 2 ) , где р_п и p_{n + 1} - подряд идущие простые числа. Тогда гипотеза Брокарда формулируется как:

^{А п} = ^п ( pL ) ^{- п} ( Р 2 ) ^ 4.

Пусть р 2 = n ².

Докажем справедливость соотношения (62) для простых чисел-«близнецов», когда расстоя- ние между подряд идущими простыми числами pn+1 - Pn = 2 — минимально. В случае, когда соседние простые числа не «близнецы», доказа- тельство очевидно.

Итак, вводя определение A _в :

А в = ( р „ + 2 ) 2 - р 2 = 4 р „ + 4 = 4 ( n + 1 ) ,      (63)

имеем

А _в = 4 n + 4 = 2( А + 1), (64) т.е. А = 2 n + 1 включен в интервал А _в .

Из (64) следует, что всегда Апв > 0, ибо на большем, чем А интервале, как было показано при доказательстве гипотезы Лежандра, всегда есть простое число.

Учитывая, что при pn = n ² на интервале ( р 2, р 2 _{+ 1} ) МСЧ и ПСЧ образуются такими же простыми числами, как и на интервале ( n ², ( n + 1)² ) , справедливо следующее соотношение:

4 ( n + 1 ) f,     .2 , _ч 1 Г z М

^А в = —6—" |^{( 1 -} z ) ^{+( 1 -} р ⁾⁺ 3 ^ 1 ^- 2 J . ⁽⁶⁵⁾

Покажем, что даже при минимуме выражения в фигурных скобках гипотеза Брокарда под- тверждается.                           1 г z \

На самом деле минимум (1 -z) +-11 -—1 = = 0,188, а минимум (1 -p) = 0,908 достигается при максимуме p = 0,0919.

Тогда необходимо найти n , при котором выполняется неравенство:

4( n + 1),              _х

⁽    ) ( 0,908 + 0,188 ) > 4.         (66)

Очевидно, что при n >  5, неравенство (66) выполняется всегда.

Решение проблемы «простых близнецов»

Используя соотношение (39), покажем, что число «простых близнецов», т.е. простых чисел, разность между которыми равна 2, бесконечно. Для этого в выражении (39) вычтем количество простых чисел, равное количеству составных чисел вида {6к ± 1}, к = 1, 2, 3, ..., находившихся на интервале (0, n). Тем самым мы учтем все простые числа, стоящие «против» составных чисел и, таким образом, не являющиеся «близнеца- ми» простых.

Здесь необходимо отметить, что «против»

составных чисел могут также оказаться и другие составные. Таким образом, вычитая удвоенное количество составных, мы как бы искус- ственно занижаем количество простых чисел-«близнецов» на интервале (0, n) путем учета уже учтенного.

Итак, оценка количества простых чисел-«близнецов» на интервале (0, n) записывается в виде:

n пв (n, z )> 2

2     11

1 - 2 z + z - p +---- z

или

n пв ( n, z )> J z

• ² - 13 z + ¹ + ( 1 - p ) . (68) 6    3

Нетрудно показать, что квадратное уравнение в скобках (68) имеет только мнимые корни. Это означает, что n _B ( n , z ) >  0 всегда.

В результате, мы пришли к выводу о том, что число простых чисел-«близнецов» на интервале (0, n ) стремится к бесконечности при n ^ да , тем самым решив вторую проблему Ландау.

В заключение отметим, что представление механизма формирования составных чисел в виде аддитивных арифметических прогрессий дало возможность предложить конструктивный метод оценок количества простых чисел, содержащихся на различных интервалах. В результате было предложено новое соотношение для оценки количества простых чисел, содержащихся на интервале (0, n). В свою очередь, это дало возможность решить две открытые проблемы математики – доказать гипотезу Лежандра и гипотезу простых чисел «близнецов», а также доказать гипотезу Брокарда и по новому подойти к подтверждению постулата Бертрана.