Метод определения фазового сдвига квазигармонических сигналов, основанный на анализе огибающей
Автор: Яковлева Татьяна Викторовна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы и анализ данных
Статья в выпуске: 6 т.41, 2017 года.
Бесплатный доступ
В работе развивается новый метод решения задачи высокоточного измерения фазового сдвига между двумя квазигармоническими сигналами на основе анализа и обработки выборочных значений амплитуды, или огибающей сигналов, которая подчиняется статистическому распределению Райса. При этом анализируются данные амплитуд трех сигналов: двух квазигармонических сигналов, разность фаз которых измеряется, и сигнала, формируемого суммой двух исходных сигналов. Измеряемый фазовый сдвиг вычисляется как угол треугольника, стороны которого соответствуют исходным, восстановленным на фоне шума значениям амплитуд указанных сигналов. Важная особенность предлагаемого метода состоит в том, что искомые фазовые характеристики определяются в результате проведения лишь амплитудных измерений, что означает существенное снижение технических требований к используемому оборудованию и упрощает практическое применение метода. Для восстановления не искаженных шумом значений амплитуд сигналов, необходимого для реализации данного способа измерения разности фаз, предлагается использовать методы и алгоритмы так называемого двухпараметрического анализа райсовских данных. В работе представлено математическое обоснование предлагаемого метода, а также приводятся результаты численного эксперимента. Предлагаемый метод является значимым для широкого круга прикладных задач, решаемых в различных метрологических устройствах и системах связи, работающих на основе анализа оптических сигналов, распространяющихся по разным каналам.
Измерение фазового сдвига, распределение райса, выборки измерений, квазигармонический сигнал, метод моментов
Короткий адрес: https://sciup.org/140228692
IDR: 140228692 | DOI: 10.18287/2412-6179-2017-41-6-950-956
Текст научной статьи Метод определения фазового сдвига квазигармонических сигналов, основанный на анализе огибающей
Решение задачи измерения разности фаз двух сигналов является значимым в различных областях науки и техники, таких как радиофизика, оптика, радиолокация, радионавигация и т.д. Такие измерения разности фаз используются при определении расстояний, в системах дальнометрии, при определении геометрических параметров объектов, при решении задач неразрушающего контроля и в ряде других прикладных задач [1–3].
Проблема высокоточного измерения разности фаз двух сигналов является предметом научных исследований в течение десятилетий, и за это время было разработано много различных методов ее решения, в частности, такие как метод компенсации фазы, способ преобразования интервала времени в напряжение [2], цифровая технология подсчета количества импульсов [4, 5], способ измерения фазы при преобразовании частоты [2, 4], группа корреляционных методов [2, 4, 6], метод, основанный на преобразовании Фурье с последующим извлечением фазовой составляющей [4, 7–9] и т.п.
Некоторые из существующих методов измерения фазы априорно используют модель гармонического синусоидального сигнала [1], т.е. предполагают, что величина амплитуды сигнала является постоянной, что не соответствует действительности. На практике, как правило, имеют дело с так называемыми квази-гармоническими сигналами, которые из-за неизбежного воздействия гауссовского шума характеризуются наличием случайных флуктуаций величины амплитуды сигнала. Такие изменения амплитуды существенно понижают точность измерения фазы [2, 10] ввиду амплитудно-фазовой модуляции. Для измерения фазы квазигармонического сигнала было разработано несколько различных параметрических способов [11 – 13], основанных на вычислениях достаточно большого числа параметров сигнала, в силу чего реализация этих методов требует значительного объема вычислительных ресурсов.
Развиваемый в настоящей работе оригинальный метод измерения разности фаз двух сигналов принципиально отличается от известных методов прежде всего тем, что он не связан с какими-либо априорными предположениями и полностью основан на обработке результатов выборочных измерений лишь величины амплитуды, или огибающей анализируемых сигналов.
Постановка задачи, основные обозначения
Для решения задачи измерения разности фаз между двумя квазигармоническими сигналами уточним ис- пользуемые понятия. На практике неизбежное воздействие шума на процесс распространения любого исходно гармонического сигнала приводит к случайным флуктуациям величины амплитуды сигнала. Таким образом, следует рассматривать квазигармонический, или квазисинусоидальный сигнал, вместо синусоидального сигнала. В каждый момент времени t такой сигнал может быть представлен в следующей форме:
x ( t ) = R ( t ) • sin ( to t + ф ( t )), (1)
где to - частота, R ( t ) - амплитуда, или огибающая сигнала, которая изменяется случайным образом под воздействием гауссовского шума, величина ф ( t ) фазового сдвига также изменяется во времени случайным образом под воздействием шума.
Для удобства графического представления сигнала рассмотрим сигнал (1) в комплексной плоскости как комплексную величину, обозначив ее S ( t ):
S ( t ) = R ( t ) • exp |^ i ( to t + ф ( t ) ) ] = = 5 ( t ) • exp ( i to t ) .
Для измерения фазовых характеристик сигналов мы будем анализировать «медленную» составляющую сигнала 5 ( t )= R ( t ) ^ exp[ i ф ( t )]. Обозначим «медленную» составляющую исходного гармонического, не искаженного шумом комплексного сигнала как вектор A ( A , ф 0). Этот вектор характеризуется постоянной величиной амплитуды A и фазы ф о . Распространение сигнала по какой-либо среде неизбежно сопровождается его зашумлением, а именно: действительная A cos ф о и мнимая A sin ф о - составляющие исходного сигнала независимо изменяются под воздействием большого числа случайных шумовых составляющих. Обозначим как F ( г , у ) суммарный вектор шума, который накладывается на исходный сигнал A и искажает его. Компоненты r x , r y вектора шума F являются независимыми случайными величинами и подчиняются нормальному распределению: Г = Г = 0, r x 2 = r y2 = о 2, где величина о2 представляет собой дисперсию шума. Очевидно, что амплитуда r шумового вектора и его у распределены следующим образом: случайная величина амплитуды r подчиняется статистическому распределению Рэлея, в то время как фаза у шумовой компоненты распределена равномерно на интервале (0,2 п ).
Обозначим как вектор R ( R , ф ) «медленную» составляющую результирующего сигнала, формируемого суммированием исходного гармонического сигнала A и шума F : R = A + F (рис. 1).
Действительная и мнимая составляющие вектора R могут быть представлены в следующем виде:
R cos ф = A cos ф 0 + r cos у ,
R sin ф = A sin ф 0 + r sin у .
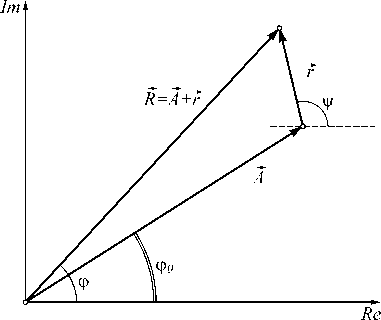
Рис. 1. Иллюстрация формирования райсовского сигнала R = |R | как результата воздействия гауссовского шума г на исходно детерминированный сигнал А с амплитудой A
Статистическое распределение случайных величин амплитуды R и фазы φ результирующего сигнала R определяется их совместной функцией распределения [17], которая описывается следующей формулой:
W ( R , ф ) d R d ф = х
2 по
х exp
A 2 + R 2
- 2 AR cos ( ф-ф 0 )
2 о
- R d R d ф .
Из формулы (3) следует, что распределения амплитуды R и фазы ф результирующего сигнала не являются независимыми, причем фаза ф результирующего сигнала, в отличие от фазы у шумовой составляющей, уже не является равномерно распределенной величиной.
Интегрируя выражение (3) по фазе ф в пределах от 0 до 2 п, получаем следующее выражение для функции распределения амплитуды R результирующего сигнала R = A + Г :
2п
W R ( R ) d R = d R I W ( R , ф ) d ф =
- ( R 2 + A 2 ) /2о 2
e .
_ R d R ( RA
= „2 ^ I 0 I _2 о V о
При получении выражения (4) было использовано интегральное представление для модифицированной
1 2f функции Бесселя, [15]: 10 (z) = ezcostdt. Из выра-
2п о жения (4) следует, что амплитуда R квазигармониче-ского сигнала удовлетворяет распределению Райса с параметрами A, о2, совпадающими с величиной амплитуды исходного гармонического сигнала A и дисперсией искажающего его гауссовского шума о2. Функция плотности вероятности райсовской случайной величины R дается формулой:
R ( R 2 + A 2 ) ( RA )
P ( R A , о ) = — exp I--—— 1 1 . (5)
о 2 V 2 о 2 J V о 2 )
Таким образом, под влиянием шума амплитуда A исходного вектора сигнала А становится случайной величиной R = | R |, которая подчиняется статистическому распределению Райса. Тем самым обосновывается применимость для решения поставленной задачи методов, разработанных для анализа райсовских данных и основанных на особенностях статистического распределения Райса.
Очевидно, что случайные изменения амплитуды результирующего сигнала влекут за собой фазовые флуктуации, что препятствует точному измерению фазовых характеристик квазигармонических сигналов.
Сущность предлагаемого метода измерения разности фаз квазигармонических сигналов
Поставленная задача состоит в измерении фазового сдвига между двумя квазигармоническими сигналами, которые распространяются в разных каналах. Величина разности фаз двух таких сигналов определяется различием в условиях распространения анализируемых сигналов (различие длины каналов или различие показателей преломления каналов распространения сигналов и т.п.) и является индикатором того или иного исследуемого процесса или объекта. Таким образом высокоточное измерение фазового сдвига квазигармонических сигналов в режиме on-line является значимой задачей в различных областях метрологии, оптики, в системах связи и т.д.
Представим квазигармонические сигналы, разность фаз которых должна быть измерена, в виде векторов R 1 ( R 1 , ф 1 ) и R 2 ( R 2 , ф 2), как показано на рис. 2.
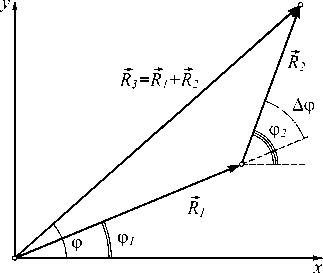
Рис. 2. Векторное представление сигналов, анализируемых при расчете искомой величины фазового сдвига Аф
Как показано выше, амплитуды этих квазигармо-нических сигналов R 1 и R 2 представляют собой случайные величины, которые подчиняются статистическому распределению Райса с параметрами ( A 1 , о 2) и ( A 2 , о 2) соответственно, где A 1 и A 2 - величины амплитуд исходных, не искаженных гауссовским шумом гармонических сигналов, о 2 - дисперсия гауссовского шума, искажающего сигналы при их распространении по соответствующему каналу.
Естественно предположить, что величина дисперсии шума одинакова для обоих каналов распространения сигналов, хотя представленный ниже математический анализ задачи может быть обобщен на слу- чай различных величин дисперсии гауссовского шума в каналах распространения сигналов. При дальнейшем рассмотрении задачи мы будем использовать априорную информацию о том, что искомая разность фаз Аф = ф2-ф1 между рассматриваемыми сигналами однозначно определяется физическими свойствами исследуемого объекта или процесса.
Зашумленные сигналы, которые измеряются в ходе решения поставленной задачи, можно представить в виде следующих векторов:
R = A + rv
R 2 = A + 42, где векторы A1 и A2 представляют собой «медленные» составляющие двух исходных, не искаженных шумом сигналов, 4,42 — векторы шума, характеризующие соответствующие каналы распространения сигналов. Очевидно, что разность фаз Аф между двумя сигналами равна углу между соответствующими векторами (рис. 2).
Рассмотрим третий сигнал, который равен сумме анализируемых сигналов R 1 и R 2 и, соответственно, представлен на рис. 2 вектором R 3 = R 1 + R 2. Мы также можем представить вектор R 3 в виде суммы R 3 = A 3 + г , , где вектор A 3 = A 1 + A 2 представляет собой сумму векторов, отображающих два исходных неискаженных сигнала. Векторы R 1 , R 2 и R 3 формируют треугольник, а искомая разность фаз Аф между двумя сигналами может быть определена из этого треугольника на основе измеренных сторон треугольника, т.е. величин амплитуд трех указанных сигналов. Однако флуктуации амплитуд сигналов, обусловленные влиянием шума, не позволят точно определить искомую разность фаз. Другими словами, стороны треугольника, образованного векторами R 1 , R 2 и R 3 , из-за воздействия шума на анализируемые сигналы постоянно флуктуируют случайным образом, что не позволяет определить искомый фазовый сдвиг, определяемый как один из углов данного треугольника, с достаточной точностью, поскольку неизбежное воздействие шума искажает сигналы, т.е. векторы, образующие треугольник. Соответственно, амплитуды этих векторов, полученные в результате измерений, дают искаженную величину искомого фазового сдвига.
Очевидно, что искомая разность фаз между сигналами A 1 и A 2 могла бы быть определена точно только из треугольника, сформированного не искаженными шумом величинами амплитуд A 1 , A 2 , A 3 , т.е. для точного расчета фазового сдвига необходимо «заморозить» представленный на рис. 2 треугольник, образованный анализируемыми сигналами, в состоянии, когда амплитуды сигналов «очищены» от шума.
Как было показано выше, амплитуды сигналов R1 и R2 подчиняются распределению Райса с райсов- скими параметрами (Ai, о2), i =1,2. Что касается третьего - суммарного сигнала R3 = A3 + г,, то, как мож- но строго доказать, его амплитуда также является случайной райсовской величиной с параметрами распределения (A3,2о2), где A3 = | A3|. В силу того, что результаты выборочных измерений амплитуд R1, R2 и R3 представляют собой искаженные данные для сторон треугольника, эти данные должны быть проанализированы и обработаны таким образом, который позволил бы восстановить не искаженные шумом значения амплитуд A1, A2, A3. Эти исходные значения амплитуд A1, A2, A3 совпадают со значением соответствующего райсовского параметра для каждого из трех сигналов. Другими словами, необходимо определить значения райсовских параметров каждого из анализируемых сигналов. Такая возможность высокоточного оценивания значений райсовских параметров обеспечивается методами так называемого двухпараметрического анализа райсовских данных [16– 19]. Эти методы позволяют рассчитать как параметр сигнала (Ai, i =1,2,3), так и параметр шума (о2) на основе обработки результатов выборочных измерений райсовской случайной величины.
В качестве примера приведем формулы для вычисления искомых райсовских параметров двухпараметрическим методом моментов [18, 19], основанным на анализе данных выборочных измерений 2-го и 4-го моментов и в силу этого обозначаемого как ММ24.
Известно, что для 2-го и 4-го начальных моментов случайной величины x , подчиняющейся распределению Райса с параметрами ( A , о 2), справедливы следующие формулы [18]:
x2 = 2-о2 + A2, x4 = 8 -о4 + 8 -о2 - A2 + A4.
Формулы (6) представляют собой простую систему двух уравнений для двух неизвестных A и о 2. В решении данной системы и состоит двухпараметрический метод моментов, основанный на измерении 2го и 4-го моментов анализируемой величины [18].
Из формул (6) для определения искомых райсовских параметров A и о2 нетрудно получить следую- щие выражения:
A 2 = x 2 V1 - 1 ,
о2 = у (1- V1—7).
В выражениях (7) введено обозначение:
x 4
t = —--1.
( x 2)2
Нетрудно видеть, что для любой случайной величины x в силу с тох а стичности величины x 2 вы по лн яется условие x 4 - ( x 2)2 > 0, так как разница x 4 - ( x 2 )2 определяет дисперсию случайной величины x 2. Поэтому введенный параметр t растет с ростом стоха-стичности процесса и удовлетворяет соотношению:
0< t < 1. Предельный случай t =1 соответствует частному случаю распределения Райса – распределению Рэлея, когда присутствует шум, а полезный сигнал отсутствует ( A =0).
На рис. 3 представлены результаты компьютерного моделирования решения задачи анализа райсовских данных, формируемых выборочными измерениями огибающей сигнала, методом моментов ММ24.
Численный эксперимент проводился следующим образом. Генерировались данные, подчиняющиеся распределению Райса, на двумерной сетке, узлы которой соответствуют различным исходно заданным значениям райсовских параметров: величины амплитуды A неискаженного сигнала и величины дисперсии шума о 2. Используя выборки значений огибающей в каждой точке сетки, вычислялись значения вышеуказанных параметров на основе разработанного алгоритма, соответствующего методу ММ24.
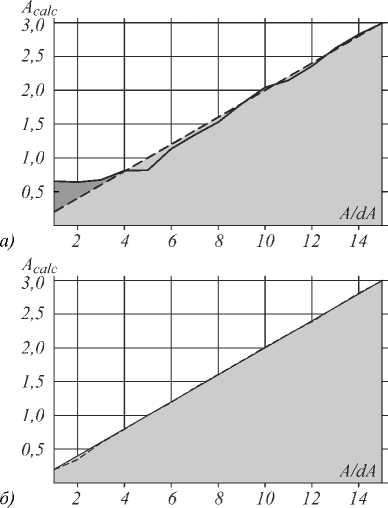
Рис. 3. Результаты численного расчета параметра A посредством двухпараметрического метода моментов ММ24: а ) а = 1,2, n = 16, A изменяется в диапазоне от 0,2 до 3,0 с шагом 0,2; б) а = 0,4, n = 16, A изменяется в диапазоне от 0,2 до 3,0 с шагом 0,2
Графики, представленные на рис. 3, получены в результате расчета параметра A методом ММ24. При этом исходные значения величин обоих параметров A изменялись в диапазоне от 0,2 до 3,0 шагом 0,2 (по оси абсцисс отмечены точки отсчета). Длина выборки n измерений случайного сигнала составляла 16. Графики соответствуют данным вычислений искомых параметров, усредненным по 50 выборкам (в реальных системах визуализации число усредняемых выборок составляет, как правило, 103 ~ 104). На рис. 3а, б показаны зависимости отклонений расчетных значений параметра Acalc от реальной, исходно заданной величины этого параметра A при различных исходных значениях параметра о. Значения по оси абсцисс на обоих графиках соответствуют точкам отсчета исходно заданных значений параметра A, а по оси ординат – расчетным значениям данного параметра Acalc.
Отклонения ломаной кривой от прямой линии на обоих графиках характеризуют точность расчетов. Графики получены для значений σ = 1,2 (рис. 3 а ) и σ =0,4 (рис. 3 б ) соответственно.
Графики на рис. 3 отображают зависимость точности расчетов по методу ММ24 от значения отношения сигнала к шуму: с ростом параметра A , т.е. при перемещении слева направо вдоль расчетных кривых, происходит увеличение отношения сигнала к шуму, и точность расчетов заметно растет, причем диапазон относительно высокой точности вычислений определяется условием A / σ≥ 1,5÷2.
Таким образом, представленные на рис. 3 графические результаты численного эксперимента позволяют продемонстрировать возможность восстановления величины амплитуды исходного сигнала на фоне гауссовского с достаточно высокой точностью и, следовательно, возможность расчета искомого фазового сдвига путем использования описанного выше метода двухпараметрического анализа райсовских данных ММ24. Этот метод является весьма простым, но вместе с тем эффективным инструментом восстановления полезной составляющей амплитуды сигнала на фоне гауссовского шума и представляет собой один из ряда методов двухпараметрического анализа райсовских данных.
Другие методы двухпараметрического анализа райсовских данных, развитые и обоснованные в работах [16– 19], включают в себя двухпараметрический метод максимума правдоподобия [16, 19] и метод моментов, основанный на обработке результатов измерений 1-го и 2-го моментов анализируемой величины [17– 19]. Эти методы, наряду с методом ММ24, обеспечивают высокую точность при решении задач разделения шумовой и информативной компонент анализируемого сигнала.
Таким образом, применяя методы двухпараметрического анализа райсовских данных для каждого из трех рассматриваемых сигналов, мы можем восстановить исходную величину амплитуды каждого из сигналов, не искаженную шумом (параметр A i , i = 1,2, 3).
Вычисление не искаженных шумом значений амплитуд всех трех сигналов позволяет «заморозить» представленный на рис. 2 треугольник в очищенном от шума состоянии и тем самым рассчитать величину искомого фазового сдвига с высокой точностью из простых геометрических соображений по формуле:
. f A 32 - A i2 — A 2
∆ϕ = arccos 3 1 2
-
I 2 A 1 A
.
Ниже представлены некоторые результаты численного моделирования предлагаемого метода измерения фазового сдвига. Данные, представленные в табл. 1, демонстрируют зависимость модуля абсолютной погрешности err =|∆ϕcalc – ∆ϕ| при расчете искомой разности фаз сигналов от ряда параметров, таких как количество измерений в выборке (длина выборки) и отношение сигнала к шуму. При этом используются следующие обозначения: ∆ϕcalc – величина фазового сдвига, рассчитанная по вышеописанному алгоритму, ∆ϕ – действительная (заданная) величина фазового сдвига. В численном эксперименте, результаты которого приводятся в табл. 1, эта величина была равна 1,318 радиан. В табл. 1 используются обозначения: SNR = 0,5(A1+A2) / σ – величина, характеризующая отношение сигнала к шуму, n – длина выборки. Данные, представленные в табл. 1, были получены при усреднении по Nav = 103 измерениям.
Табл. 1. Результаты численного расчета величины модуля абсолютной погрешности err = | ∆ϕ calc – ∆ϕ | при определении фазового сдвига в зависимости от отношения сигнала к шуму SNR и длины выборки n
|
SNR =102 |
SNR =0,25 103 |
SNR =0,5 103 |
SNR =103 |
|
|
n = 8 |
4,2 ⋅ 10–4 |
1,4 ⋅ 10–4 |
5,8 ⋅ 10–5 |
1,2 ⋅ 10–5 |
|
n =16 |
1,8 ⋅ 10–4 |
0,9 ⋅ 10–4 |
4,9 ⋅ 10–5 |
1,0 ⋅ 10–5 |
Заключение
В работе развивается оригинальный метод измерения разности фаз между двумя квазигармониче-скими сигналами, основанный на статистической обработке выборочных данных для амплитуд следующих трех сигналов: двух сопоставляемых квазигар-монических сигналов и их суммы. Представлен теоретический анализ задачи, проведенный с учетом того факта, что амплитуды трех анализируемых сигналов являются случайными величинами, подчиняющимися статистическому распределению Райса. Алгоритм реализации предлагаемого метода состоит в совместном восстановлении не искаженных шумом амплитуд сигналов и последующем расчете искомого фазового сдвига как угла треугольника, образованного этими амплитудами.
Таким образом, искомый фазовый сдвиг определяется в результате лишь амплитудных измерений и их математической обработки, что значительно сокращает требования к необходимому оборудованию и тем самым упрощает реализацию предлагаемого метода в различных прикладных задачах, решаемых в системах дальнометрии, связи и т.п. Эффективность предлагаемого метода измерения фазового сдвига подтверждена результатами численных экспериментов.
Работа выполнена при поддержке гранта РФФИ N17-07-00064 по программе фундаментальных исследований.
Автор выражает глубокую признательность своим коллегам профессору Г.Г. Левину и профессору Г.Н. Вишнякову за полезные обсуждения задачи.
Список литературы Метод определения фазового сдвига квазигармонических сигналов, основанный на анализе огибающей
- Кинкулькин, И.Е. Фазовый метод определения координат/И.Е. Кинкулькин, В.Д. Рубцов, М.А. Фабрик; под ред. И.Е. Кинкулькина. -Москва: Советское радио, 1979. -280 с.
- Чмых, М.К. Цифровая фазометрия/М.К. Чмых. -Москва: Радио и связь, 1993. -184 с. -ISBN: 5-256-01043-3.
- Смирнов, В.Н. Широкополосный цифровой фазометр/В.Н. Смирнов, М.В. Кучеров//Вопросы радиоэлектроники. -2004. -Т. 1, № 1. -С. 33-41.
- Electrical measurement, signal processing, and displays/ed. by J.G. Webster. -Boca Raton: CRC Press, 2004. -723 p. -ISBN: 978-0-8493-1733-0.
- Mahmud, S.M. Error analysis of digital phase measurement of distorted waves/S.M. Mahmud//IEEE Transactions on Instrumentation and Measurement. -1989. -Vol. 38, Issue 1. -P. 6-9. - DOI: 10.1109/19.19989
- Liang, Y.R. Fundamental limits on the digital phase measurement method based on cross-correlation analysis/Y.R. Liang, H.Z. Duan, H.C. Yeh, J. Luo//Review of Scientific Instruments. -2012. -Vol. 83(9). -095119. - DOI: 10.1063/1.4751867
- Mahmud, S.M. High precision phase measurement using reduced sine and cosine tables/S.M. Mahmud//IEEE Transactions on Instrumentation and Measurement. -1990. -Vol. 39, Issue 1. -P. 56-50. - DOI: 10.1109/19.50416
- Mahmud, S.M. High precision phase measurement using adaptive sampling/S.M. Mahmud//IEEE Transactions on Instrumentation and Measurement. -1989. -Vol. 38, Issue 5. -P. 954-960. - DOI: 10.1109/19.39036
- Sedlacek, M. Digital measurement of phase difference -a comparative study DSP algorithms/M. Sedlacek, M. Krumpholc//Metrology and Measurement System. -2005. -Vol. 12, Nr 4. -P. 427-448.
- Игнатьев, В.К. Параметрический анализ колебаний с медленно меняющейся частотой/В.К. Игнатьев, А.В. Никитин, С.В. Юшанов//Известия вузов. Радиофизика. -2010. -Т. 53, № 2. -С. 132-145.
- Игнатьев, В.К. Измерение фазового сдвига квазигармонических сигналов/В.К. Игнатьев, А.В. Никитин, С.В. Юшанов//Вычислительные методы и программирование. -2013. -Т. 14. -С. 424-431.
- Ramos, P.M. A new sine-fitting algorithm for accurate amplitude and phase Measurements in two channel acquisition systems/P.M. Ramos, A.C. Serra//Measurement. -2008. -Vol. 41, Issue 2. -P. 135-143. - DOI: 10.1016/j.measurement.2006.03.011
- Hing, Ch.S. Two accurate phase-difference estimators for dual-channel sine-wave model/Ch.S. Hing, Zh. Zhenhua//EURASIP Journal on Advances in Signal Processing. -2013. -Vol. 2013. -122. - DOI: 10.1186/1687-6180-2013-122
- Рытов, С.М. Введение в статистическую радиофизику. Ч. 1. Случайные процессы/С.М. Рытов. -Москва: Наука, 1976. -494 с.
- Абрамовиц, М. Справочник по специальным функциям. С формулами, графиками и математическими таблицами/М. Абрамовиц, И. Стиган. -М.: Наука, 1979. -832 с.
- Yakovleva, T.V. Noise and signal estimation in MRI: two-parametric analysis of rice-distributed data by means of the maximum likelihood approach/T.V. Yakovleva, N.S. Kulberg//American Journal of Theoretical and Applied Statistics. -2013. -Vol. 2, Issue 3. -P. 67-79. - DOI: 10.11648/j.ajtas.20130203.15
- Yakovleva, T.V. Methods of mathematical statistics in two-parameter analysis of Rician signals/T.V. Yakovleva, N.S. Kulberg//Doklady Mathematics. -2014. -Vol. 90(3). -P. 675-679. - DOI: 10.1134/S1064562414070060
- Яковлева, T.В. Обзор методов обработки магнитно-резонансных изображений и развитие нового двухпараметрического метода моментов/Т.В. Яковлева//Компьютерные исследования и моделирование. -2014. -Т. 6, № 2. -С. 231-244.
- Яковлева, T.В. Теория обработки сигналов в условиях распределения Райса/Т.В. Яковлева. -М.: Вычислительный центр им. А.А. Дородницына Российской академии наук, 2015. -268 с.


