Метод определения электропроводности растворов кислот и оснований

Исследование электропроводности имеет большое значение при изучении процессов сольватации и транспортных свойств ионов в растворах электролитов. Особенно интересными являются растворы кислот и оснований, так как ионы гидроксония и гидроксила движутся по эстафетному механизму, а механизм движения противоионов неэстафетный:

H 3 O ⁺ + H 2 O о H 2 O + H 3 O ⁺ .                      (1)

OH - + H 2 O о H 2 O + OH - .                     (2)

В процессе (1) ионы H 3 O ⁺ группируют 4 молекулы воды [1]. При этом отрицательные заряды диполей воды направлены к H 3 O ⁺ , что облегчает туннельный переход протона H ⁺ в H 3 O ⁺ к молекулам воды и далее.

В случае процесса (2) ионы OH - ориентируют 2 молекулы H ₂ O положительными зарядами диполей. Тогда за счет туннельного эффекта ионы H ⁺ из H 2 O переходят к иону OH - .

Эти процессы и объясняют аномально высокую электропроводность растворов кислот и оснований.

Метод определения электропроводности растворов кислот и оснований

На кафедре «Неорганическая и аналитическая химия» ВСГУТУ разработана плазменно-гидродинамическая концепция состояния ионов в растворах электролитов. В рамках данной теории получено уравнение для теоретических оценок электропроводности водных растворов электролитов [2]:

N_Ae ² exp( — — ) • 1,11 • 10 ^—12

A      Э 7 T⁷ ’          7  17

Л =___________ k B ___________, Ом - см моль - .

6nnR_s (1 + R s -)

rD

Для кислот и оснований остается неформализованной величина R_s . Обзор литературы показал, что значения радиусов гидратированных ионов H 3 O ⁺ и OH ^— вообще отсутствуют. Приемлемых методов теоретических оценок этих величин, соответствующих данным Стокса, нет.

Эффективные радиусы этих гидратированных ионов формализуются известной задачей механики [3] о системе, состоящей из одной частицы с массой M и n частиц с одинаковыми массами m .

Если исключить движение центра инерции, то проблема сводится к задаче движения n частиц с M - массой ионов H 3 O ⁺ или OH ^— ; m - массой молекул воды; n s - гидратным числом.

^

Рассматривается гидратный комплекс, в котором R - радиус-вектор H 3 O ⁺ или

OH ; R a a = (1,2,3,..., n ) - радиус вектор

комплексе. Расстояние от H 3 O ⁺ или OH

гидратированных молекул воды в гидратном до молекул в этом комплексе обеспечивается

выражением:

^ ^

r a = ^R a

^

^{— R} ,

а начало координат в центре инерции формализуется равенством:

^

^

M • R + m У R a = 0.

a

Очевидно, введение в уравнение (5) значения R_a из [4] дает безразмерное равенство в оригинальной постановке задачи

R

m

У r_a    M + n s • m

a

— ■

.

Гидратированные ионы имеют центрально-симметричное распределение вещества и заряда, и при их движении под действием внешнего поля меняется система отсчета. Тогда возможно умножение левой и правой частей уравнения (6) на величину R a • M . Далее в левую часть уравнения (6) вводится значение r_a из выражения (4), что приводит к следующему уравнению:

^ ^

^

У Г =У1 Ra — R | = n • Ra as

^

— R .

a

a

В этом случае

^ ^

R • R a

^ n s • R a

—

M • m ^ — • M =-- R a .

r       M + ns • m

Наглядная трансформация векторных величин к их скалярам в виде модулей можна в виде

^ ^                  ^ ^ ^ ^

R • R a • M =-- ( n_sR a • R a — R • R a ).

M + ns • m

^   ^               о                    ^   ^

Угол между векторами Ra и Ra равен a = 180 , а между векторами R и Ra — воз-

a

0⁰. Тогда, согласно правилам векторного анализа, скалярное произведение двух векторов равно произведению их модулей на cos а (где a - угол между направлениями этих век-

→→                    →→ торов). Поэтому R⋅ Ra = -R ⋅ Ra, так как cos1800 = -1 и R⋅Ra=R⋅R ввиду того, что cos00 = 1.

Приведенные факты дают основание следующему представлению

R ⋅ R a   = ^M ⋅ ^m ⋅ ^{R a} .                               (8)

R + n_s ⋅ R_a M + n_s ⋅ m M

Таким образом, приведенная симметричная форма выражения (8) в скалярных ар-

M⋅m гументах с учетом приведенной массы системы, равной          , показывает, что

M + n_s ⋅ m

R⋅R a = r есть эффективный приведенный радиус системы. R+ns ⋅Ra

8 см [5],

Радиус молекулы воды в жидком состоянии при 298 K равен R = 1,15 ⋅ 10

радиус R + =1,35 ⋅ 10 - ⁸ см и радиус R H ₃ O                              OH

- 8                                          H O +

=1,53 ⋅ 10 ⁸ см [4]. Далее гидратное число n_s^{H 3 O} = 4

[1] и n_s^{OH -} = 2,2 из уравнения (8) при r_i =1,53 ⋅ 10 - ⁸

При этих значениях R , R_a и n_s эффективные радиусы ионов H ₃ O + и OH - равны:

R s ( H 3 O + )

1,35 ⋅ 10 ^{- 8} ⋅ 1,15 ⋅ 10 ^{- 8}

1,34 ⋅ 10 ^{- 8} + 4 ⋅ 1,15 ⋅ 10 ^{- 8}

= 0,261 ⋅ 10 ^{- 8}

см,

R s ( OH ) =

1,53 ⋅ 10 ^{- 8} ⋅ 1,53 ⋅ 10 ^{- 8}

1,53 ⋅ 10 ^{- 8} + 2,2 ⋅ 1,15 ⋅ 10 ^{- 8}

= 0,43 ⋅ 10 ^{- 8}

см.

Результаты исследования

Полученные значения радиусов гидратированных ионов H ₃ O + и OH - могут быть использованы при оценке электропроводности водных растворов кислот и оснований. Результаты теоретических оценок эквивалентных электрических проводимостей растворов электролитов в рамках плазменно-гидродинамической модели по уравнению (3) приведены в таблицах 1, 2 и на рисунках 1, 2. Литературные значения Λ _лит взяты из [6].

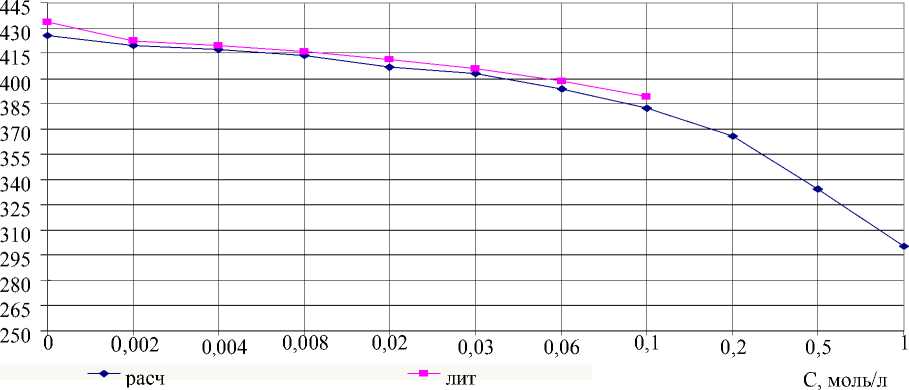
Рис. 1. Графическая зависимость электропроводности Λ водного раствора HBr от концентрации при 298K

Λ, Ом-1∙см2∙моль-1

	•--------------<	.—__:			1---—
									^------■
-

0,5       1

0,001 0,002 0,005   0,01    0,02    0,03    0,05    0,1     0,2     0,3

расч

—■— лит

С, моль/л

Рис. 2. Графическая зависимость электропроводности Λ водного раствора KOH от концентрации при 291К

Таблица 1

Концентрационная зависимость эквивалентной электропроводности ( Λ , Ом - ¹ ⋅ см² ⋅ моль - ¹) HCl при 291K

µ = 9,24; r_s ^Kt = 0,26 ⋅ 10 - ⁸см; r_s ^An = 1,34 ⋅ 10 - ⁸см; r_s ^прив = 0,22 ⋅ 10 - ⁸см

C, моль/л	0	0,001	0,01	0,1	5	10
Х = ( z kt z an ⋅ С / µ )1/2	0,000	0,010	0,033	0,104	0,736	1,040
exp( - 0,84 ⋅ X )	1,000	0,991	0,973	0,916	0,539	0,418
rD = 0,02814( ε T / C )1/2	∞	48,50	15,34	48,50	6,85	4,85
Λ теор	372	367	361	340	146	91
Λ лит	378	377	370	351	150	66

Таблица 2

Концентрационная зависимость эквивалентной электропроводности (Λ , Ом - ¹ ⋅ см² ⋅ моль - ¹) NaOH при 291K

µ = 9,75; r s ^Kt = 1,75 ⋅ 10 - ⁸ см; r s ^An =0,43 ⋅ 10 - ⁸см; r s ^прив = 0,345 ⋅ 10 - ⁸см

C , моль/л	0	0,001	0,01	0,1	10
Х = ( z kt z an ⋅ С / µ )1/2	0,000	0,010	0,32	0,319	1,011
exp( - 0,82 ⋅ X )	1,000	0,992	0,973	0,764	0,427
rD = 0,02814 ⋅ ( ε T / С )1/2	∞	136,5	43,16	4,315	1,3647
Λ теор	226	223	216	159	18,000
Λ лит	220	208	200	160	20,0

Заключение

Таким образом, полученные значения электропроводности кислот и оснований на основе плазменно-гидродинамической модели состояния ионов в растворах электролитов, учитывающие теоретически оцененные радиусы гидратированных ионов H3O+ и OH-, имеющих центрально-симметричное распределение вещества и заряда, хорошо коррелируют с литературными данными.