Метод определения натяжения сетеполотна антенн на основе распознавания образов

Одной из основных тенденций развития космических аппаратов (КА) является установка на них крупногабаритных параболических антенн, позволяющих существенно повысить качество приемо-передачи информации. При этом данные антенны должны быть конструктивно совместимы с габаритно-весовыми ограничениями космического аппарата и головного обтекателя. Цля обеспечения такой совместимости наиболее распространенным подходом в отечественной практике является показ, при котором в конструкцию антенны закладывается многозвенное трансформирование (двух-, трехколенное складывание ребер зонтичной конструкции) с использованием сетеполотна [1; 2] для формирования отражающей поверхности.

Однако такой подход порождает еще одну проблему -обеспечение заданной формы параболоида после раскрытия. В существующих решениях поверхность раскрытого параболоида претерпевает серьезные деформации, а неравномерное натяжение сетеполотна может привести к неравномерности его электродинамических свойств, что значительно снижает эффективность КА в целом.

Цля предупреждения таких деформаций при наземно-экспериментальной отработке антенн необходимо обеспечивать равномерное натяжение сетеполотна и его достоверный контроль.

Задача контроля величины и равномерности натяжения сетеполотна осложняется тем, что сетеполотно обладает весьма сложными анизотропными упругопластичными свойствами. Затрудняет задачу контроля и то, что при отладке антенны, когда сетеполотно растянуто на крупногабаритном рефлекторе, непосредственный доступ к нему ограничен или вовсе невозможен. По имеющимся данным, как в отечественной, так и в международной практике не обнаружено методов решения этой проблемы. Методы, применяемые в других областях, например в машиностроении, в данном случае не применимы из-за необходимости непосредственного контакта датчика с объектом.

Существующие методы определения натяжения сетеполотна позволяют проводить измерения вручную лишь при непосредственном контакте с сетеполотном, что делает невозможным их использование для крупногабаритного рефлектора. При этом они трудоемки и субъективны, а следовательно, недостаточно точны и экономически неэффективны. Поэтому существует потребность в автоматизации процесса измерения натяжения сетеполотна.

Цля решения этой проблемы наиболее целесообразно использование информационно-измерительных систем распознавания образов [3], обладающих такими преимуществами, как возможность дистанционного контроля при больших расстояниях между системой и объек том, отсутствие сил влияния на объект со стороны измерительной системы, быстродействие, возможность многопараметрического контроля, а также точность и стабильность измерений. При этом функционирование таких систем во многом определяется алгоритмами обработки и анализа графической информации.

Таким образом, объектом исследования является информационно-измерительная система определения усилия натяжения сетеполотна, а предметом - методы и алгоритмы обработки информации в этой системе.

Сетеполотно антенны изготовлено из двух скрученных вместе золоченых вольфрамовых нитей, каждая из которых имеет диаметр 15 мкм [1]. Сетеполотно, растянутое на рефлекторе, должно иметь номинальное натяжение 4...6г/см (рис. 1).

Рис. 1. Образец сетеполотна в натянутом состоянии [1]

Рассмотрим структурную схему информационно-измерительной системы (рис. 2). На техническую систему, подвергаемую контролю, - изделие из сетеполотна - датчик и систему управления влияют факторы внешних воздействий Z : освещение, температура, влажность и т. п.

Цатчиком является первичный преобразователь информации (фотокамера). Из общего информационного потока Х датчик выделяет лишь часть информации Х , отбрасывая остальную. Обработчик информации формирует экспертную информацию ^ ² на основе обработки и анализа первичной информации Х . При этом, после каждой обработки информации размерность информационного потока сокращается: М¹ >М >  М . В предлагаемой системе измерения усилия натяжения обработка фотоизображения х = I ( х , у ) текстуры сетеполотна ведется с помощью специального программного обеспечения на ЭВМ, результатом обработки является информация об усилии натяжения X² = ( T _ , T_h ) сетеполотна, г / см, состоящая из вертикального и горизонтального компонентов.

Таким образом, предметом исследования в данной статье является модель процесса обработки информации -X1 = (X1, F(Р), Z), где F(Р) - оператор преобразования информации в датчике; Р - множество параметров настройки обработчика информации; Z - характеристики искажений обработчика информации. На результат влияет множество условий, учет которых классическими методами моделирования весьма затруднен. Поэтому было принято решение о применении нейросетевых алгоритмов для определения величины натяжения сетеполотна.

Анализ деформации сетеполотна позволил выделить два существенных механизма изменения его структуры под действием натяжения: изменение размеров ячейки и изменение геометрической формы внутри ячейки, заключающееся в затягивании узлов, распрямлении участков петель и пр.

Для определения размеров ячейки по изображению сетеполотна разработаны и исследованы алгоритмы на основе преобразования Радона и на основе автокорреляционной функции изображения [4]. Эти алгоритмы обладают значительной помехоустойчивостью, но если определять с их помощью по фотографии сетеполотна удлинение ячейки, то значение удлинения будет представлено в относительных единицах (пикселях). Очевидно, что числовое значение размера ячейки в этом случае зависит от масштаба фотографии. Кроме того, из-за гистерезиса линейных деформаций размеры ячейки не дают однозначного представления об усилии натяжения сетеполотна.

Для достижения инвариантности результатов обработки к масштабу изображения в качестве информативной характеристики была выбрана деформация формы ячейки. При этом решалась задача распознавания, заключающееся в определении параметров модели путем сопоставления наблюдаемых данных А = I ( х , у ) и результатов моделирования ^² = ( ф , T_h ).

Как правило, задача распознавания образов [4] состоит из следующих этапов: получение образа, первичная и вторичная обработка (предобработка), извлечение признаков, классификация.

В нашем случае получение образа - это этап фотографирования сетеполотна.

Первичная обработка изображения заключается в преобразовании цветного изображения I к полутоновому виду и разбиении на М непересекающихся одинаковых блочных фрагментов В.. Такая фрагментация необходима для уменьшения неоднородности освещения и фона, так как внутри малого фрагмента их влияние сказывается незначительно. Затем внутри каждого фрагмента проводится вторичная обработка: компенсация не равномерного освещения, удаление крупномасштабных помех с помощью вейвлет-фильтрации, подавление шумов медианным фильтром.

Следующим шагом алгоритма является извлечение аффинно-инвариантных признаков . Для достижения инвариантности к масштабу и сдвигу объекта на изображении с помощью дистантного преобразования бинаризи-рованного фрагмента В ( х , у ) находятся веса D ( х,у ) всех пикселей фона изображения В ( х , у ) = 0. Эти веса равны евклидову расстоянию от данного пикселяа фона с координатами В ( х , у ) = 0 до ближайшего пикселя тона В ( х , у ) = 1. Так, пиксели, находящиеся в центре б о льших «дыр» обладают б о льшими весами. Далее для инвариантности к масштабу изображения производится нормировка значений D ( х , у ) в диапазон D ( х , у ) е [0; 1], и те веса пикселей, которые меньше заданного порога T , приравниваются к нулю.

После этого на матрице дистантного преобразования D находятся координаты центров масс образовавшихся областей. Эта процедура основана на алгоритме восьмисвязной заливки.

Однако для обеспечения одинакового масштаба необходимо определить размер области вокруг центра петли. Для достижения единого масштаба эта область должна быть пропорциональна размеру ячейки на изображении.

Для каждой ячейки на изображении находятся четыре ближайшие к ней ячейки. После этого вокруг центра каждой ячейки очерчивается окружность с радиусом 4

R q = 7 Z d m-n, i ,                    (1)

⁴ i = 1

где d _min^. - расстояния до центров ближайших четырех ячеек. Краевые ячейки на изображении в расчет не принимаются. Соответственно этой окружности из предоб-работанного изображения вырезается круг с центром, совпадающим с центром большой петли ячейки.

Далее этот круг помещается в квадратную матрицу со строго заданными размерами 128 • 128 пикселей. Размеры матрицы должны выбираться из ряда 2 " , где и = 5, 6...8, что необходимо для дальнейшего вычисления быстрого преобразования Фурье.

Так, для каждой к -й ячейки на фрагменте В,j = 1,2...,М изображения I (исключая краевые петли) мы получаем ее собственное единомасштабное, центрированное изображение C _q , решая тем самым проблему инвариантности к сдвигу и масштабу текстуры сетеполотна. Суммируя все изображения C _q и нормируя значения яркостей

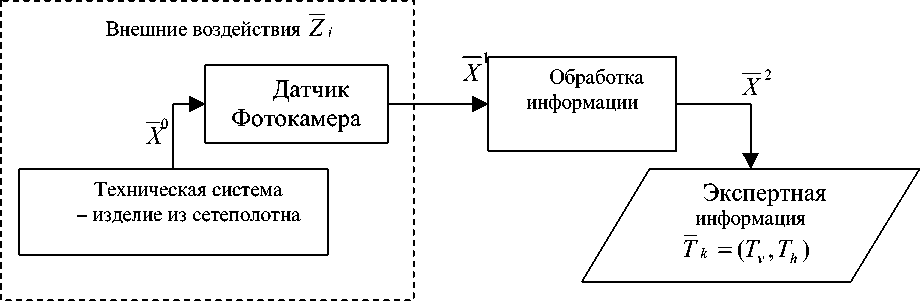
Рис. 2. Модель информационно-измерительной системы измерения и управления параметрами

пикселей суммарного изображения, получаем усредненное центрированное изображение петли SUM . по всему фрагменту ^ изображения / (рис. 3):

Q

SUM j = „ £ C q , j = 1, M , (2) ^Q q = 1

где Q - количество ячеек в фрагменте В, исключая краевые ячейки; C _q - центрированное изображение отдельной ячейки размером 128 • 128 пикселей.

Для достижения инвариантности к повороту изображение SUMячейки из декартовых координат (х,у) преобразуется в полярные координаты (г, ф), 3де радиус г берет начало в центре изображения. Вычислив амплитудную характеристику преобразования Фурье от такой развертки изображения и взяв 100 первых наибольших низкочастотных коэффициентов (3,4), получим вектор признаков, инвариантных к преобразованиям сдвига, поворота и масштабирования (рис. 4). Как показала дальнейшая работа с нейронными сетями, большее или меньшее количество амплитуд, взятое для эталонно-калибровочного набора (учебника) нейросети, не ведет к значительному улучшению качества обучения. Более того, если для учебника выбрано больше 120 гармоник, то обучение занимает довольно много времени и не приводит к желаемому результату.

M • 360

F ( и , v ) =

M —1 N —1

£ £ SUM ⁽ г , ф ) exp ⁽ - i 2^п(— + —Д, _m r =0 ф=0                       M 360 ⁽³⁾

и = 0... M - 1, v = 0...359,

A ( и , v ) = || F ( и , v )||, и , v = 1,10,

v j = A ( и , v ), i = 1,100, j = 1, M .

В качестве классифицирующей процедуры использовались слоистые нейронные сети [3] и корреляционный классификатор.

Нейронная сеть состояла из двух слоев: десять нейронов в первом слое и два нейрона во втором. Подстройка весов синапсов проводилась методом обратного распространения ошибки. Обучающая выборка для нейросети состояла из входных векторов v . _k , z = 1, 2,., 100, вычисленных для каждой фотографии I_k , и выходных значений натяжения T_k = ( T _ , T_h ) .

Действие корреляционного классификатора основано на последовательном вычислении коэффициента корреляции между тестовым образом и эталоном. Решение о принадлежности тестового образа к некоторому классу выносится по максимальной величине коэффициента корреляции.

Описанные алгоритмы легли в основу программного обеспечения [5] для обработки фотоизображений сете-полотна, расчета усилия натяжения и визуализации результатов.

^Ш । ।

-2-10122-166

Рис. 4. Матрица логарифмированных значений амплитудного спектра изображения. Квадратом выделена область низкочастотных коэффициентов (подматрица размером 10 • 10 элементов), которые были взяты для построения учебника

Методика определения натяжения включает три основных этапа: калибровку классификаторов для заданного типа сетеполотна, фотографирование сетеполотна, расчет усилий натяжения и построение топограмм натяжения по фотографии при помощи программного обеспечения. Рассмотрим методику калибровки подробнее.

В ходе экспериментальных работ по калибровке классификаторов было произведено фотографирование тестового образца сетеполотна типа плетения «Атлас», размером 20 • 20 см с различным усилием натяжения: от 0 до 10 г / см - по каждому из двух взаимно ортогональных направлений, с шагом по A T = 1г / см. Для равномерного распределения натяжения в сетеполотне после каждого нагружения производилась релаксация сетеполотна - вибрация в течение 15 мин с частотой 50 Гц.

Фотографирование производится при рассеянном освещении с помощью цифрового фотоаппарата «Canon EOS 20D», на расстоянии 30 см до сетеполотна, с использованием штатива, при этом оптическая ось объектива была перпендикулярна плоскости сетеполотна. Так был получен эталонно-калибровочный набор (учебник), состоящий из 121 изображения I _k , к = 1,2, .121 (0,1,2., 10 г / см включительно для двух направлений) размером 3 504 • 2 336 пикселей. Из этого набора формировался входной набор признаков v . ^ z = 1,2, ., 100, вычисленных

а                                       б                                        в

Рис. 3. Матрица . О ( х , у ) дистантного преобразования ( а ); исходное изображение 5 ( х , у ) текстуры сетеполотна (крестиками помечены центры ячеек) ( б ); усредненное центрированное изображение ячейки SUM ( в )

для каждой фотографии I . Выходные значения натяжения T_k = ( Т _ , T_h ) задавались на специальном стенде при натяжении образца.

Обучение производилось один раз при заданных условиях для заданного типа сетеполотна. После обучения нейронной сети проводилось еетестирование на тех фотографиях, которые не вошли в учебник.

Допустим, что натяжение на эталонном образце распределяется однородно. Определим ошибку классификации как среднее значение разности эталонного значения натяжения, установленного на стенде, и значения, полученного классификатором при усреднении значений натяжения по всему изображению:

N

Err = АkZ T У - T ] , (5)

N i = 1

где ^ = 121 - количество испытаний; Т - значение усилия натяжения, полученное в результате расчетов; Т - эталонное значение усилия натяжения.

Так как величина натяжения 1 состоит из двух компонентов: вертикального Т и горизонтального T _h , в таблице представлены ошибки определения натяжения по вертикали и горизонтали, вычисленные после тестирования алгоритмов.

На основании этих данных можно сделать вывод, что классификатор на основе корреляционной меры сходства по точности уступает нейросетевому Это связано с тем, что коэффициент корреляции отражает лишь вероятностные свойства спектра изображения, в то время как нейросетевая модель учитывает влияние внешних факторов благодаря включению в учебник примеров, содержащих помеху.

В качестве примера представлены топограммы для фотографии сетеполотна размером 1 800 • 1 800 пикселей с эталонным натяжением Т = 3,8; 6,5 г/см, построенные с помощью корреляционного (рис. 5) и нейросетевого (рис. 6) классификаторов соответственно.

На топограммах оттенками серого цвета обозначены значения условного погонного натяжения. В каждом случае размер блочного фрагмента составляет 200 пиксе лей. Меньший размер фрагмента позволяет получить более детальные топограммы. Значительные локальные отклонения на детальных топограммах вызваны неоднородностями в плетении сетеполотна, так как встречаются участки с более вытянутыми ячейками, с искажением формы и размеров. Они различимы даже невооруженным глазом. Эти области относительно стабильны, т. е. они не исчезают после вибрации или длительного растяжения на стенде. Их наличие может быть объяснено особенностями самой технологии плетения полотна, влиянием колебаний температуры, влажности и прочих воздействий внешней среды на технологический процесс. Эти дефекты вносят довольно весомый вклад в погрешность определения натяжения.

В данной статье в качестве выходных значений классификатора использовалась величина условного погонного натяжения сетеполотна. Однако если включить в учебник нейросети в качестве выходных данных параметры электродинамических характеристик сетеполотна, то можно получить возможность контроля электродинамических параметров. Основная сложность в этом случае заключается в в точном измерении величин электродинамических характеристик сетеполотна при различном усилии натяжения при калибровке системы.

Таким образом, авторами был разработан метод определения натяжения сетеполотна , основанный на применении методов обработки, анализа, нейросетевой классификации текстурных фотоизображений сетеполотна и позволяющий проводить бесконтактный автоматизированный контроль натяжения на этапах раскроя сетеполотна, сборки и отладки рефлектора в условиях производства. В рамках этого метода созданы два алгоритма: алгоритм, позволяющий формировать признаки изображения, инвариантные к его масштабу и сдвигу, и алгоритм, позволяющий формировать признаки изображения, инвариантные к повороту объекта, основанный на применении двумерного преобразования Фурье к изоб-

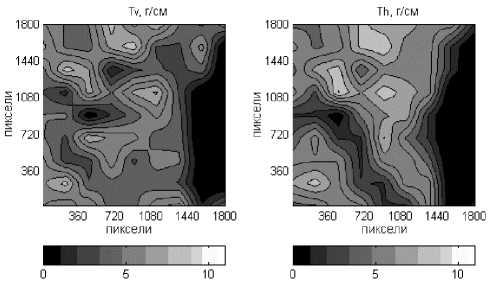
Рис. 5. Топограммы значений условного погонного натяжения сетеполотна, построенные с помощью корреляционного классификатора

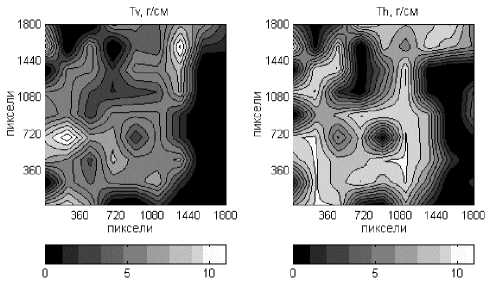
Рис. 6. Топограммы значений условного погонного натяжения сетеполотна, построенные с помощью нейросетевого классификатора

Относительная ошибка классификации

Тип классификатора	Средняя ошибка, %		Максимальная ошибка, %
	ErC v	Erc h	Еп'.	Erc h
Нейросетевой	19,5	15,6	66,3	27,3
Корреляционный	33,5	16,4	75,9	57

ражению в полярных координатах. Предложена методика обучения нейронной сети, позволяющая формировать эталонно-калибровочный набор (учебник) для калибровки программного обеспечения системы определения натяжения сетеполотна.