Метод определения оптимального пространственного направления сосудов в задаче восстановления 3D топологии коронарной системы

Исходными данными задачи реконструкции пространственного изображения кровеносной системы сердца человека являются последовательности кадров ангиографической съемки в формате DICOM. Основным методом технологии восстановления пространственных древовидных объектов является одновременная трассировка и анализ изображений сосудов на проекциях с параллельным восстановлением пространственной топологической и геометрической структуры дерева сосудов. Задача решается в несколько этапов [1-4]. На начальном этапе производится синхронизация последовательностей кадров и выделяется необходимая для восстановления структуры фаза сердца. Данные процедуры позволяют компенсировать сокращения и смещения сосудов во время съемки. Далее производится геометрическая пространственная привязка проекций (рис. 1) и составление композитных кадров, что связано с произвольной ориентацией и движением камеры во время съемки. На этапе трехмерной трассировки осуществляется анализ патологических изменений сосудов, формы разветвлений, и восстанавливается сложный профиль внутренней области сосудов. На заключительном этапе строится и отображается на экране в произвольной проекции поверхность сосудов. Трехмерное изображение сосудов дает полное представление об их структуре и позволяет выявлять и диагностировать патологические изменения. Указанный выше комплекс методов восстановления пространственной топологогеометрической структуры сосудов позволяют построить эффективную компьютерную систему для диагностики и мониторинга заболеваний сердца.

Метод выбора оптимального направления движения по сосуду в трехмерном пространстве, представленный ниже, лежит в основе алгоритма построения трехмерной трассы сосуда – алгоритма пространственной трассировки. Метод включает анализ пространственных интенсивностей при помощи сферы возможных направлений. Предлагается два метода обнаружения минимумов интенсивностей на сфере. Данный подход позволяет производить восстановление пространственных объектов по малому числу наблюдаемых проекций.

a)                            б)

Рис. 1. Геометрическая пространственная привязка проекций и реконструкция пространственного изображения

Общие принципы пространственной трассировки

По сути, пространственная трассировка является обобщением принципов двумерной трассировки [1]. Расположив в пространстве изображения проекций, с помощью алгоритма обратного проецирования мы получим некоторое пространственное распределение интенсивности. Для выбора оптимального направления движения производится анализ критериальной функции f xyzR рр, у ) , распределенной на сфере радиусом R с центром в точке ( x,y,z ) . Сферу с распределенной на ней критериальной функцией в дальнейшем будем называть сферой возможных направлений, подразумевая то, что на ее основе будет производиться выбор оптимального направления движения на каждом шаге (рис. 2).

В простейшем случае эта сфера является срезом пространственной интенсивности.

Построение полусферы возможных направлений движения в пространстве

Для анализа пространственной интенсивности и выбора направления движения используется полусфера возможных направлений. Пусть также дана точка p0 (x0, y0,z0) пространства, которая является текущей точкой трассы сосуда. Будем считать заданным начальный вектор vоVx,Vy,vz), соответствующий начальному направлению движения в пространстве. По- строение полусферы возможных направлений происходит следующим образом. Введем новую систему координат O'X'Y'Z' в пространстве, таким образом, что ось O'Z' будет сонаправлена с вектором vо, то есть плоскость O'X'¥' будет перпендикулярна ему. Точка O' в координатах мировой системы координат будет совпадать с текущей точкой трассы. В координатах новой системы координат уравнение сферы запишется в виде x2 + у2 + z2 = R2. При этом нас будет интересо- вать только верхняя полусфера, поэтому накладывается дополнительное условие z > 0.

Рис. 2. Пример полусферы возможных направлений

По аналогии с двумерным случаем [5] набор интенсивности на поверхности полусферы может производиться несколькими способами: набор пространственной интенсивности собственно точек сферы; набор с усреднением по лучам; набор пространственной интенсивности с усреднением по конусу; набор с усреднением по цилиндру. Выбор методов набора обуславливается качеством изображений проекций, а также методом поиска минимумов на сфере, представленным ниже.

На втором этапе определения оптимального направления движения необходимо найти область минимальной интенсивности, центр которой и даст искомое пространственное направление по сосуду. Разработано два подхода к поиску минимумов: метод, основанный на квадратичной аппроксимации интенсивностей, и метод, основанный на гауссовой аппроксимации гистограммы.

Метод, основанный на квадратичной аппроксимации интенсивностей. Поиск локальных минимумов здесь основан на аппроксимации функции (обозначим ее I(x,y) в пределах скользящей маски квадратичной поверхностью F = ax ² + by ² + cxy + dx + ey + f . Далее мы определяем точку минимума функции F(x,y) . Если такая точка существует и лежит достаточно близко к центру маски, то она фиксируется. Стандартный метод нахождения минимума функции двух переменных состоит в нахождении критической точки

df    af .

из условия — = 0, — = 0 и проверки выполнения в дx     6у ней достаточных условий минимума:

5 2F . д² F б²F I д² F

—z- > 0, — ---— ---- > 0.

а x ²      а x ² а у ^{2 д x д}у ,

В нашем случае вторые частные производные являются константами:

а ² f „ д ² f     д ² F

—г = 2 a , —г = 2 b , __ = c д x ²        д у ²      д x д у

.

Это позволяет дополнительно сократить объём вычислений.

Рис. 3. Результат работы алгоритма

Так как нельзя требовать близости к началу координат меньше, чем на 1 отсчет (в силу дискретизации и наличия шумов), то получаем не отдельные точки минимумов, а группы точек вокруг истинной точки минимума. Если количество точек в группе мало, то эта группа игнорируется – этот минимум ложный, полученный за счёт влияния шумов. В результирующий список точек локальных минимумов заносится по одной точке (центру тяжести) из каждой группы. На примере, изображённом на рисунке 3, имеем 6 точек, которые обозначены цифрами.

Метод, основанный на гауссовой аппроксимации гистограммы. В общем случае задачу можно сформулировать в следующем виде. Необходимо выделить на изображении области со сходными свойствами (аналог задачи кластеризации). В качестве меры «похожести» предлагается использовать распределение интенсивностей внутри отдельных однородных областей. Данный метод основан исключительно на анализе распределения интенсивностей. Он производит разбиение всех точек изображения на классы, принадлежность к которым определяется только интенсивностью в данной точке.

Пусть у нас имеется изображение, представленное в виде двумерного массива распределения интенсивностей I(x, у). Будем предполагать, что изображение представляет собой набор однородных по интенсивно- сти областей, имеющих гауссово распределение яркостей. Построим ненормированную гистограмму hi = h (i), показывающую количество точек данного цвета i, которые встречаются на изображении. Будем считать, что две точки принадлежат од- ному классу, если их яркости при аппроксимации гистограммы функциями Гаусса аппроксимируют- ся одной и той же функцией. В общем виде задача формулируется так.

2 j = 0

N - 1

2 Ai ' 2 i = 0 ⁱ

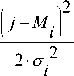
- h . ^j

V                            ?

N ^ min где N - число классов; M i - математическое ожи- дание в i -м классе; ai - дисперсия в i -м классе; Ai - коэффициент. После разбиения на классы в качестве локальных минимумов выбираются те классы, для которых выполняется условие: Mmin < Ms, s e S, где Mmin - математическое ожидание внутри класса; S - множество соседей данного класса. Минимум на полусфере возможных направлений задает нам направление движения в трёхмерном пространстве.

Заключение

Алгоритм выбора оптимального направления является одним из основополагающих алгоритмов пространственной трассировки. Он был использо- ван при реализации компьютерной системы восстановления трехмерной структуры коронарных артерий сердца. Следует отметить, что наличие двух альтернативных методов обнаружения минимумов интенсивности позволяет повысить надежность и точность выбора оптимального направления движения по сосуду. Их последовательное применение позволяет скомпенсировать недостатки, присущие каждому из алгоритмов, и работать стабильно в условиях различных входных данных.