Метод определения принципиальных мод маломодового оптического волокна на основе применения многоканального ДОЭ

В настоящее время вследствие недостатка ресурсов одномодового оптического волокна (SMF) в линейном режиме для передачи растущих объёмов информации [1,2] большой интерес вызывает реализация телекоммуникационных систем на основе мультиплексирования с модовым разделением каналов (MDM) [3–6]. Технология MDM предполагает использование маломодового волокна (FMF), которое имеет осесимметричную структуру и в отличие от многосердцевинных волокон (MCF) может быть изготовлено по стандартной промышленной технологии. С математической точки зрения использование пространственных мод ОВ, переносящих различный орбитальный угловой момент (OAM), приводит к появлению дополнительного базиса ортогональных функций, доступного для модуляции и мультиплексирования полезных сигналов.

Однако при передаче заданной линейной суперпозиции мод по ОВ существенной длины происходит их случайное смешение [7–9], описываемое комплексной частотно-зависимой матрицей распространения ОВ. В результате совместного действия смешения мод и межмодовой дисперсии (МД) возникает эффект межмодовой интерференции, который не позволяет надёжно передавать мультиплексированный по модам сигнал в ОВ без применения ресурсоёмкой цифровой обработки сигнала по технологии MIMO.

В [10] было показано, что по аналогии с концепцией принципиальных состояний поляризации (ПСП) [11], на которой базируется теория поляризационной модовой дисперсии (ПМД) в SMF [12, 13], может быть введён базис из N ортогональных пространственных мод, называемых принципиальными модами (ПМ), которые не подвержены МД первого порядка и остаются ортогональными на выходе ОВ. По определению, входные и выходные ПМ представляют собой собственные функции соответствующих операторов групповой задержки и могут рассматриваться как са-мовоспроизводящиеся модовые пучки для ОВ с де- фектами (флуктуациями границы сердцевина-оболочка, макро- и микроизгибами). Концепция применения ПМ в телекоммуникационных системах была проанализирована в [14, 15], где авторы показали принципиальную возможность их использования в качестве базиса ортогональных несущих. Авторы статьи [16] расширили модель ПМ на пространство Стокса, обобщив тем самым формализм, разработанный для описания ПМД, на базис пространственных мод.

Однако в настоящее время, насколько нам известно, не предложено каких-либо методов, позволяющих в реальных условиях однозначно определять комплексную матрицу распространения ОВ и базисы входных и выходных ПМ. Для решения данной задачи в настоящей статье мы предлагаем метод, основанный на оптическом корреляционном анализе и представляющий собой метод JME [13, 17], расширенный на базис пространственных мод ОВ.

1.    Модель распространения сигнала по ОВ в обобщённом пространстве Джонса

При построении модели все оптические сигналы будем считать узкополосными в окрестности несущей частоты © 0 , а нелинейные эффекты пренебрежимо малыми. В качестве среды распространения рассмотрим ОВ со ступенчатым профилем показателя преломления, поддерживающее N пространственных мод при данном значении © 0 . С одной стороны, ступенчатый профиль, являясь наиболее простым, не предполагает минимизации смешения мод и дифференциальной групповой задержки (ДГЗ), и потому удобен для численной проверки эффективности предлагаемого метода. С другой стороны, FMF со ступенчатым профилем часто рассматривается в качестве среды передачи для реальных систем с MDM [18–20]. Таким образом, далее электромагнитные (ЭМ) поля будем представлять в базисе мод Бесселя.

В приближении слабонаправляющего ОВ (Δn < 1%) [21] может быть получен базис LP-мод Ep q(r, z) = e-i ep qz Ep q(r), каждая из которых содержит множитель e±'p ф и переносит OAM, пропорциональ- ный азимутальному индексу p [5, 22, 23]. Здесь и далее r = (r, ф), Рpq - коэффициент распространения моды с индексами p, q.

Поскольку собственные моды ОВ E _pq ( r ) образуют базис ортогональных функций, мы можем описывать распространяющееся в волокне ЭМ излучение как с помощью поперечного распределения поперечной составляющей электрического поля:

E ( r ) = S a pq E pq ( r ),                              (1)

p,q так и с помощью соответствующего комплексного вектора |a), представляющего собой разложение данного поля по собственным модам.

Распространение ЭМ поля через линейную среду, поддерживающую N пространственных мод, можно представить с помощью выражения [10]

s out^ a out^ — e ' U ( - ) s 'n p in ),                             (2)

где | а '” ) и | a™‘ ) - комплексные единичные вектора размера N х 1, определяющие ЭМ поле на входе и выходе ОВ соответственно, s '” и s out - соответствующие действительные значения амплитуды, U ( - ) - матрица распространения ОВ размера N х N , ф ( ш ) описывает общие для всех мод затухание и фазовый сдвиг.

Согласно кусочно-регулярной модели, полная матрица распространения ОВ может быть выражена в следующем виде [9]:

и ( - ) — П K ,U⁽ k ⁾ ( ” ),                            (3)

к — 1

где U ⁽ k ) ( - ) - матрица распространения к -го участка с длиной L ^{( k )} , которая не должна существенно превышать длину корреляции для данного ОВ.

Будем считать, что смешение мод определяется, в первую очередь, изгибами волокна и эллиптичностью сердцевины, учитывая при этом поворот плоскости изгиба между последовательными участками ОВ на случайный угол @ . Таким образом, каждую матрицу U ^{( к} ) ( - ) представим как произведение двух матриц:

U ⁽ k ) ( - ) = V ⁽ k ) Л ⁽ k ) ( - ),                                  (4)

где частотно-зависимая матрица Л ^{( к} ) ( - ) описывает распространение через k -й участок ОВ, включая эффекты ДГЗ, дифференциальных модовых потерь (MDL) и смешения мод, а частотно-независимая матрица V ^{( k )} на входе k -го участка описывает его поворот по отношению к предыдущему.

Пренебрегая смешением между модами, распространяющимися в прямом и обратном направлениях, уравнение смешения запишем в следующем виде [8]: d a

dz              v где . и v - мультииндексы, определяемые соответствующими значениями азимутальных и радиальных индексов, a. - коэффициенты в модовом разложении поля, образующие вектор |a\ и K.v - коэффициенты смешения. Представляя (5) в матричной форме, для каждого k-го участка можем записать:

^ = (-Г(—) + K(k)(-))| a), где

|( а , ^-а ) + ' ( Р ]^{( ш )} -Р о )     ... О

Г ( - ) =

¹ ( ^а N ^-а ) + ' ( ^Р N ^{( - )} -Р о )

В выражении (7) а и Ро - соответственно сред- ние модовые потери и среднее значение не зависящего от частоты члена в разложении коэффициента распространения в ряд Тейлора. Тогда ф в выражении (2) можно выразить как ф — - (О,5а +'Ро)L.

Считая, что Г и K ^{( k )} не зависят от z , из (6) и (2) получаем:

Л" > ( - ) — _е 1 - ^{Г (}"^+к"^(-) > « * ' .                              (9)

Используя теорию смешения поля в терминах локальных нормальных мод [8] и полагая, что радиус изгиба каждого участка много меньше его длины, для коэффициентов смешения вследствие изгиба получаем:

Sk ’ ( 6 pm -1 +5 pm .1 +6 , ,1- m ) Ovp.J

( k )

.v

Y pv ,

где ^ ⁽ k ) - кривизна к -го участка, p и m - азимутальные индексы рассматриваемых мод, 5 - символ Кронекера, и множитель Y . _v выражается следующим образом:

Y .v

х

' Y . Y v

--------- i х

2 n ₁ k ₀ a e _p e _m

^J p ^{( K} . ^a ) ^J m ^{( K} v ^a )

41 Jp-1 (K a ) Jp +1 (K a ) Jm-1 (Kv a ) Jm +1 (Kv a ) 1 ’ где a - радиус сердцевины, параметры к и у выражаются как Kpq = (коni)2 -ppq и Ypq = ^ - (ко”2)" , n1 и n2 – показатели преломления сердцевины и оболочки соответственно в точке z = О, ко = 2л/ХО - волновое число в вакууме, em =2 для m =0 и em = 1 в осталь- ных случаях.

Для коэффициентов смешения из-за эллиптично- сти сердцевины получаем

K ( k )

.v

^Z ( * ( ⁵ p , m -2 ^{+ 5} p , m +2 ^{+ 5} p ,2- m ) ( Р . -Р v )

Y .v ,

где Z(к) — I d(aXк) (z) - a(k) (z)) / dz - девиация разности между радиусами сердцевины по осям x и y на длине k-го участка. Однако, как показало численное моделирование, случайное отклонение формы сердцевины от цилиндрической даже на величину порядка единиц мкм/м приводит к пренебрежимо малому смешению мод в сравнении с изгибами ОВ.

Вследствие инвариантности мод E pq ( r ) к повороту вращение осей между секциями k и k + 1 не приводит непосредственно к смешению мод. Однако каждая вихревая мода с азимутальным индексом p претерпевает фазовый сдвиг на - р @ , где @ - случайный угол. Таким образом, матрица V ^{( k )} является диагональной с элементами v **’ = e ^{- ip 0 <} ) на главной диагонали.

2.    Принципиальные моды оптического волокна

Вывод ПМ может быть осуществлён по аналогии с феноменологическим подходом, используемым для описания ПСП в SMF [11]. Рассмотрим ЭМ поле s in | a in ) на входе ОВ на заданной фиксированной частоте. Дифференцируя выражение (2) по частоте и исключая s in | a in \ получаем:

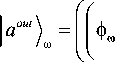
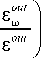
I + ¹¹ -1

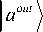
где I – единичная матрица. Запишем выходное ЭМ поле в следующем виде:

I и °' = | р °" e ^{- ,} '^ф °"'                                                (14)

и согласно определению принципиальных мод поста вим условие д |р°"')/дю = 0. Тогда можем записать:

I a °"' \ =- i ф " "'| a °"' \,                                     (15)

ю где фЮ"' = дф°"' / дю представляет собой групповую задержку тg выходной ПМ |р°"') [12].

Подставляя (15) в (13), получаем уравнение на собственные значения в пространстве Джонса, обобщённом на базис пространственных мод:

G| р°"') = т| р°"'),(16)

где матрица G , выражаемая в виде

G = - i UU1,(17)

имеет собственные значения

Ф °"'             o"Ut °"'

ю + i фю-i s ю Л и собственные вектора |р °"'\ представляющие собой выходные ПМ. По аналогии с выходными ПСП, выходные ПМ формируют базис ортогональных функций [10]. Сравнивая (13) и (15), получаем N соответствующих значений групповой задержки (ГЗ):

т g =фГ =Т о - Re[ T ],                         (19)

т.е. действительные части собственных значений т имеют физический смысл относительных ГЗ соответствующих ПМ. На основе данных значений мы можем определить ДГЗ как разность между ГЗ самой медленной и самой быстрой ПМ: Ат = т + - т - .

Дифференцируя (2) и исключая | a °"'), выразим также производную выходного вектора |a""'^ через входной вектор | a in):

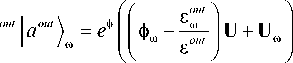
s i x a in ).     (20)

Делая аналогичную подстановку для входного вектора | a in) = |р in )e-1 ф“ и приравнивая производную выходной ПМ к нулю, с использованием (18) получаем следующее уравнение на собственные значения:

F| р") = т| р1"), которое определяет входные ПМ |р in) как собственные вектора матрицы

F = - i I I.(22)

В общем случае собственные значения т имеют также мнимую часть

1т[т] = -0,5amL -s°"' / s°"',(23)

которая обладает физическим смыслом частотнозависимых потерь на длине передачи L для соответствующей ПМ [15]. Если же пренебречь MDL, матрица распространения и ( ю ) становится унитарной [10]. Тогда матрицы F и G , которые теперь можно записать как F = - i и ^ф и _ю и G = - i U " U , становятся эрмитовыми и должны иметь действительные собственные значения т (в самом деле, если и ( ю ) унитарна, то s °"' = e ^{- 0,5 a} L s in и выражение (23) будет равно нулю).

При рассмотрении ПМ p ˆ в обобщённом пространстве Стокса [16] взаимосвязь между векторами | р ) и р может быть представлена в том же виде, что и для классических пространств Джонса и Стокса:

^р = ( р | Л| р ),                                    ⁽²⁴⁾

| р ) = ^р -Л-1 р ),                                            ⁽²⁵⁾

где Л - вектор, состоящий из D матриц Л j размером 2 N х 2 N . Данные матрицы представляют собой обобщение матриц Паули на случай D >2 в соответствии с подходом, впервые предложенным М. Гелл-Маном [24]. Таким образом, матрицы Л , ■ имеют нулевой след и должны удовлетворять условию

(1/2 N ) trace { Л i Л j } =8 i j .                        (26)

В [16] предложен алгоритм построения базиса матриц Л j для общего случая.

Таким образом, анализ матрицы распространения ОВ в пространстве Джонса позволяет определить базис его ПМ и соответствующие значения ГЗ, а также, осуществив переход в обобщённое пространство Стокса на основании формул (24)–(26), применить существующую в настоящее время теорию ПМД для случая передачи в ОВ N пространственных мод.

3.    Метод JME, расширенный на базис пространственных мод

Метод JME, впервые предложенный в [17], предусматривает анализ процесса распространения оптического сигнала в частотной области и позволяет определять одновременно вектор ПМД и матрицу Джонса размера 2х2. В рамках описанного выше подхода к моделированию маломодового режима в ОВ на основе ПМ мы предлагаем расширить метод JME на базис пространственных мод в N-мерном пространстве Джонса. Практическая реализация такого метода предполагается на основе оптического корреляционного анализа посредством реконфигурируемого многоканального ДОЭ, позволяющего непосредственно в оптическом домене определять модовый состав выходного излучения [4,7,25–29].

Для определения не только амплитуд N модовых составляющих принимаемого излучения, но и их относительных фаз, анализирующий ДОЭ, кроме N основных дифракционных порядков, должен содержать 2 N –2 дополнительных дифракционных порядков, предназначенных для получения интерферометрических суперпозиций между опорной и тестируемой модами [28–31]. Таким образом, амплитудно-фазовая функция передачи анализирующего ДОЭ будет иметь вид [32]:

^ aDOE^{( x )} = E ^E * qq ^{( X} e v"’ ⁺ p , q

+ 4 Z ( EP.. .№ E'„ ( x ) ) e""’ +          (27)

V ² Ip , q №o, q o ]

где x = ( x , y ), E _{p 0 q 0} ( x ) – поперечное распределение поля моды с фазой ф _{p o q o} , которая выбрана в качестве опорной, и векторы v _pq = ( k ₀ x _pq / f , k ₀ y _pq / f ) представляют собой пространственные частоты соответствующих дифракционных порядков в фокальной плоскости Фурье-линзы с фокусным расстоянием f .

Многоканальный ДОЭ с функцией передачи (27) может быть реализован как полностью фазовая голограмма на базе коммерчески доступных пространственных модуляторов света (SLM) [33, 34] с помощью известных алгоритмов расчёта фазовых ДОЭ, модифицированных для метода композиций [27, 29, 35].

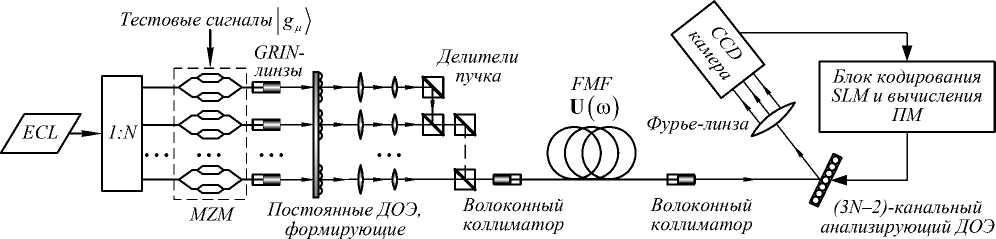
Схема реализации предлагаемого метода приведена на рис. 1. В соответствии с техникой JME для расчёта ПМ требуется восстановить матрицу U ( ® ) для ряда дискретных частот (использование не менее двух различных частот необходимо для определения матриц F и G ). Для этого на каждой частоте через ОВ должны передаваться известные линейные суперпозиции мод, задаваемые с помощью модуляторов Ма-ха-Цендера (MZM) и постоянных ДОЭ, формирующих одномодовые пучки.

⁺ Z ( ^E * 0 q 0 ^{( X )+} E ** qq ^{( x )} ) ^ ’ ’

V ² ip , q] * [p o , q o ]

на основе SLM одномодовые пучки

Рис. 1. Схема реализации метода определения матрицы распространения и принципиальных мод ОВ

Поскольку точность метода напрямую зависит от разрешения системы по частоте и низкого уровня фазового шума, перестраиваемый лазерный источник должен обладать как можно более узкой полосой излучения. Поэтому наиболее предпочтительным вариантом является использование лазерного диода с внешним резонатором (ECL), обеспечивающего ширину полосы излучения менее 100 кГц.

Очевидно, для вычисления всех N ² комплексных элементов матрицы U ( ® ) на заданной частоте необходимо решить N систем из N уравнений, каждое из которых получается в результате передачи известной линейной суперпозиции мод через ОВ. Следовательно, в этом случае вычислительная сложность будет возрастать по квадратичному закону с ростом числа мод. Для минимизации вычислительной сложности, требуемой для определения матрицы распространения, мы предлагаем следующий алгоритм, состоящий из двух последовательных этапов.

На первом этапе предполагается определение каждого отдельного ц -го столбца матрицы U ( ® ). В рамках этого процесса известные ненулевые тестирующие сигналы g _ц пропускаются через каждый ц -й мо-

довый канал, при этом в качестве опорной моды E _{p o q o} ( x ) для выражения (27) используется мода E _ц ( х ). Таким образом, мы определяем, каким образом ц -й модовый канал влияет на остальные на данной часто-

те. Тогда элементы каждого ц -го столбца матрицы распространения будут определяться как

I u vj

e ' ⁶ ""

<

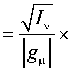
Г (

х exp - ' arctan

2 1 V'n

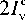
)) ^- arg ⁽ g ц )

ц , v = 1... N , "*v ; ^u цц = T I " / | ^g "I ,

где I _v - интенсивность в дальней зоне анализирующего ДОЭ в дифракционном порядке, соответствующем v -й принимаемой моде и задаваемом в выражении (27) пространственной несущей частотой v _pq ; I _v sin и I _v co описывают интенсивности в дополнительных дифракционных порядках, определяемых согласно выражению (27) пространственными частотами v ^s _p ⁱⁿ _q и v ^c _p ^o _q ^s соответственно;

I _ц - интенсивность в дифракционном порядке, соответствующем опорной моде.

В результате передачи по ОВ N тестовых сигналов получим амплитуды всех элементов матрицы распространения, а также фазы элементов каждого ц-го столбца относительно элемента ицц. Таким образом, на втором этапе достаточно определить разности фаз между столбцами матрицы распространения. Эти разности фаз могут быть извлечены путём передачи известных тестовых сигналов через каждую пару последовательных модовых каналов. Тогда при передаче тестовых сигналов с одинаковой амплитудой и фазой через модовые каналы ц и ц + 1 (ц = 1...N -1) разность фаз между соответствующими столбцами матрицы и(ю) будет определяться как фц,ц+1 =

= arg

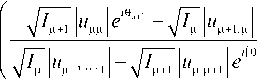
ц+1,ц+1

^ ^ц+1,ц ц+1 + 0ц,ц+1 )

где I _ц и I _{ц +1} - интенсивности в дифракционных порядках, соответствующих модам ц и ц +1; 0_{ц +1} , _ц и 0_ц , _{ц +} 1 — фазы элементов и _{ц +1} , _ц и и _ц , _{ц +1} относительно элементов и _цц и и _{ц +1} , _{ц +1}, определённые на первом этапе; 0_{ц +1} - разность фаз между модовыми каналами ц и ц +1, где ц -я мода рассматривается в качестве опорной. Значение 0_{ц +1} определяется аналогично межмодовым разностям фаз, которые определялись на первом этапе:

2 1 sin. - 1 . - 1

0 .=- arctan — ^цц------ .                  (30)

^ц+1                 О rcos т т                                V 7

² I ц+1 I ц+1 I ц

Теперь, зная относительные фазы между соседними столбцами матрицы распространения, мы можем определить все её элементы с фазами, взятыми относительно элемента u 11 :

[ и V1 = | и V1 | e ' ^{0 V 1}, V = 1... N

S                           i                              (31)

I и .ц+ 1 = и J e ⁽ "^{ц +Ф ц}"^{+ 1 )} , V = 1... N , ц = 1... N - 1.

Таким образом, мы получили в явном виде выражения для вычисления всех элементов матрицы распространения, и потребность в вычислительных ресурсах при увеличении N будет расти линейно.

Далее описанный выше алгоритм повторяется для остальных частот, что позволяет вычислить матрицы F и G и, решая уравнения на собственные значения (16) и (21), определить ПМ данного ОВ и соответствующие ГЗ.

4.    Результаты численного моделирования

На основе описанной в разделе 1 аналитической модели была разработана в среде MATLAB численная модель ступенчатого FMF в частотной области. Рассматриваемое ОВ при радиусе сердцевины 8,6 мкм и числовой апертуре 0,14 имеет нормированную частоту V =4,8806 на длине волны Х0=1550 нм и поддерживает распространение пяти пространствен- ных мод, характеризующихся различным OAM: LP–21, LP–11, LP01, LP11 и LP21. Для данного типа ОВ ДГЗ составила 5,72 пс/м для мод LP01 -LP+2i, и 3,06 пс/м для мод LP01 -LP+ii. Эффекты, связанные с ПМД, на данном этапе моделирования не учитывались.

Представленные ниже результаты моделирования были получены при следующих параметрах ОВ, соответствующих режиму сильного смешения [9]: ОВ состоит из K =4000 участков, имеющих равномерно распределённую случайную длину, при этом общая длина ОВ составила L =1002,2 м; кривизна каждого участка c.k определяется как случайная величина с нормальным распределением (для положительных значений) и СКО с_: = 1 м , параметр эллиптичности сердцевины Z k для каждого участка нормально распределён с СКО c_z = 1 мкм/м; угол поворота между секциями также имеет нормальное распределение с СКО о ® = л /18.

Поскольку коэффициенты распространения LP-мод на частотной сетке рассчитывались непосредственно из уравнения на собственные значения, результаты моделирования учитывают не только МД первого порядка, но и дисперсию высших порядков.

На рис. 2 и 3 показаны результаты моделирования соответственно для первого и второго этапов процесса определения матрицы распространения ОВ на частоте ю ₀. Считалось, что ДОЭ имеет разрешение 128 x 128 при размере пиксела 20 мкм, а фокусное расстояние Фурье-линзы f =20 см. Для повышения точности вычислений, тестирование моделируемого ОВ проводилось на трёх частотах ю ₀- Аю , ю ₀ и ю ₀ + Аю с разносом Аю =19,53125 МГц, после чего вычислялись входные и выходные ПМ согласно (16) и (21).

Согласно определению, ПМ не подвержены МД первого порядка и сохраняют ортогональность на выходе ОВ. Таким образом, корректность получаемых ПМ проверялась путём моделирования переходных влияний между модовыми каналами при передаче сигналов в базисе собственных LP-мод и ПМ. При этом использовалась схема передачи, аналогичная изображённой на рис. 1. Мы можем определить матрицы P ⁱⁿ и P ^out , столбцы которых представляют собой входные и выходные ПМ соответственно. Тогда при передаче сигнала | а ™ ) в базисе ПМ коэффициенты для собственных мод задаются вектором P '" ) | а '" ) и формируются набором MZM и постоянных ДОЭ, а на приёмной стороне восстановление сигналов в отдельных модовых каналах осуществляется с помощью N -канального ДОЭ с функцией передачи

V ,DOE ( x )= Z ; ' =1 (m ' =1 P V- * E ц ( х ) ) «”■ ■ ^, (32) где комплексные коэффициенты p Vц ' * представляют собой элементы матрицы P ^{out †} .

Полученные зависимости переходного влияния для передачи в базисе собственных мод и ПМ показаны на рис. 4 (приведены зависимости, полученные для передачи мод LP₀₁, LP₁₁ и LP₂₁, поскольку при передаче сопряжённых мод LP –11 и LP –21 зависимости носят в целом аналогичный характер).

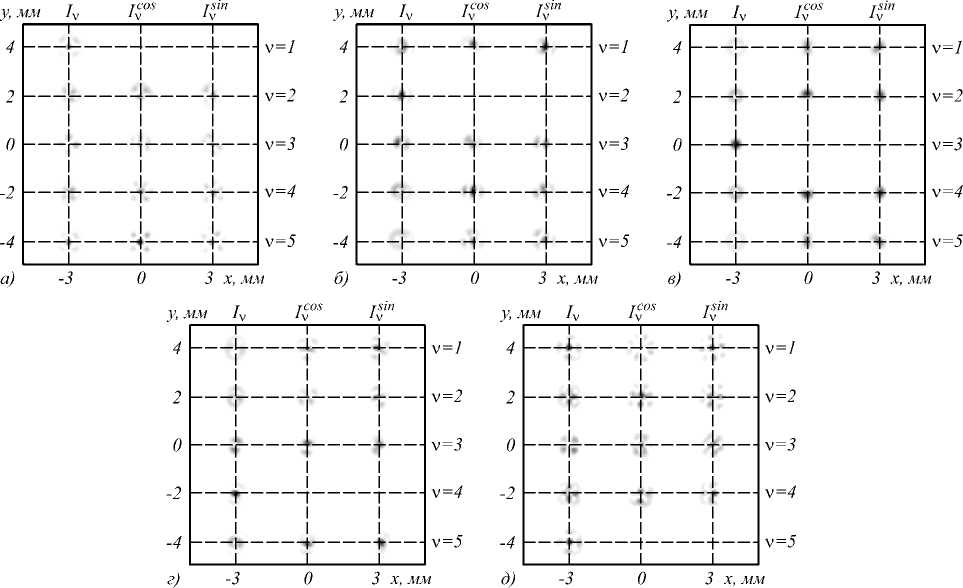
Рис. 2. Распределение интенсивности в фокальной плоскости Фурье-линзы анализирующего ДОЭ на этапе определения амплитуд и относительных фаз элементов внутри столбцов матрицы распространения при последовательной передаче тестирующих сигналов через модовые каналы LP–21 (а), LP–11 (б), LP01 (в), LP11 (г) и LP21 (д)

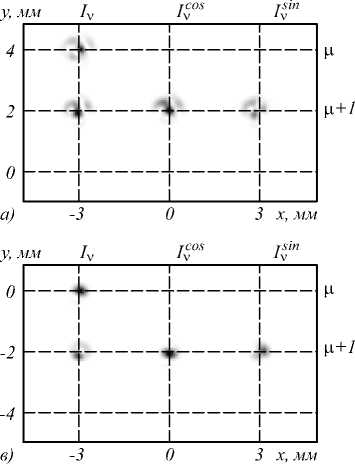
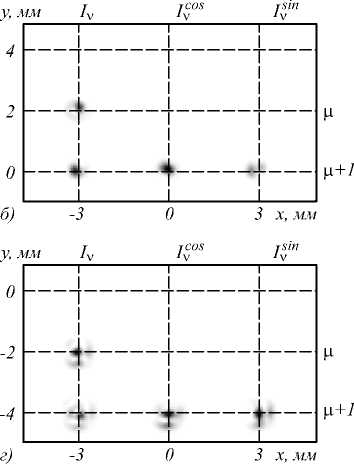
Рис. 3. Распределение интенсивности в фокальной плоскости Фурье-линзы анализирующего ДОЭ на этапе определения разности фаз между столбцами матрицы распространения при последовательной передаче тестирующих сигналов через модовые каналы LP–21 и LP–11 (а), LP–11 и LP01 (б), LP01 и LP11 (в), LP11 и LP21 (г)

Заметим, что в первом случае (рис. 4 а-в ) эффект смешения в наибольшей степени проявляется между сопряжёнными модами, что объясняется равенством их коэффициентов распространения, а наименьшее смешение наблюдается между модами LP ± 21 и фундаментальной модой.

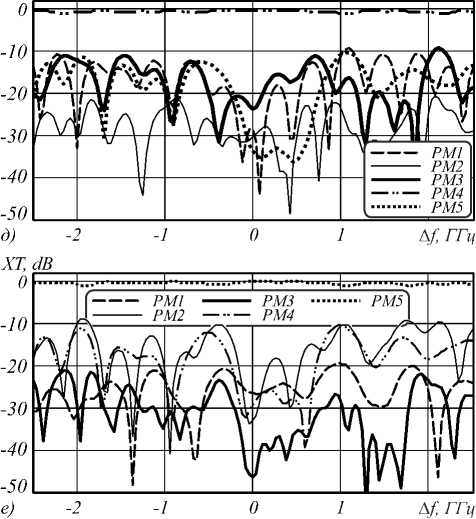
Как следует из полученных результатов , в целом переход в базис ПМ (рис . 4г-е) действительно обеспечивает существенное снижение переходных влияний между модовыми каналами в окрестности частоты ω0, что согласуется с общепринятой концепцией ПМ и свидетельствует об адекватности предложенного метода их определения. Однако, как и следовало ожидать согласно описанной в разделе 2 аналитической модели, ортогональность ПМ ограничена лишь некоторым частотным интервалом. Это ограничение связано с тем, что при выводе ПМ, как и в случае ПСП, пренебрегают дисперсионными эффектами второго и более высоких порядков. Таким образом, по аналогии с ПСП в SMF, для ПМ в FMF может быть введено понятие ширины полосы ПМ, т.е. такого частотного интервала ΔνПМ, на котором ПМ сохраняют свойства ортогональности и частотной независимости. Если оценивать эту величину для моделируемого ступенчатого FMF с позиции сохранения ортогональности по уровню пере-XT, dB

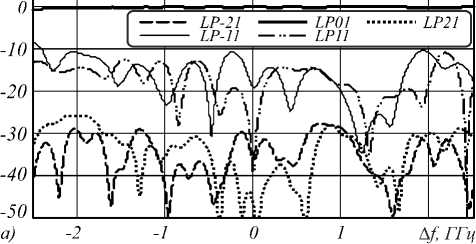
ходного влияния –20 дБ, в зависимости от конкретной

ПМ получаем значения Δν ПМ в диапазоне от 256,8 МГц (рис. 4 г ) до 352,5 МГц (рис. 4 е ). Естественно, что ширина полосы ПМ имеет на 3–4 порядка меньшие значения, чем ширина полосы ПСП в SMF [13], поскольку МД второго порядка, характеризуемая дифференциальной волноводной дисперсией, имеет гораздо более высокие значения, чем ПМД второго порядка.

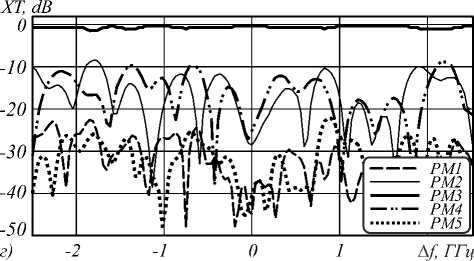
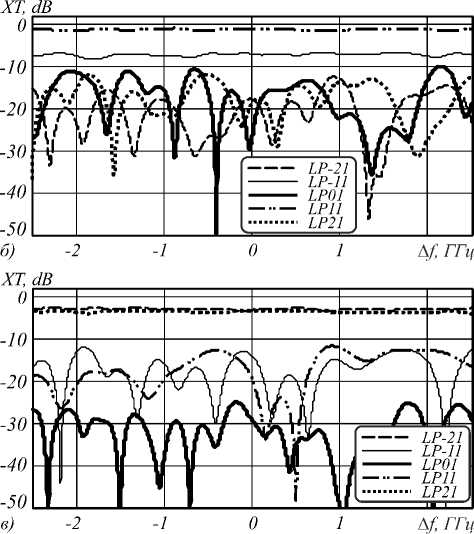
Рис. 4. Зависимости переходного влияния от частоты при воздействии на входе ОВ собственных мод LP01 (а), LP11 (б), LP21 (в) и соответствующих ПМ (г–е)

XT, dB

Тем не менее, результаты моделирования по передаче RZ-OOK сигнала в FMF данного типа на длине порядка 1 км показывают, что, несмотря на малую ширину полосы ПМ, использование базиса ПМ вместо собственных мод ОВ в качестве несущих позволяет принципиально повысить надёжность MDM-передачи со скоростью 2,5 Гбит/с [36]. Дополнительные перспективы по повышению скорости и дальности передачи информации в MDM-системах могут быть обеспечены благодаря применению FMF со специальным профилем, минимизирующим смешение мод, и простых методов цифровой коррекции, направленных исключительно на компенсацию хроматической дисперсии в отдельных каналах.

Заключение

В данной работе предложен метод определения матрицы распространения и принципиальных мод ОВ в маломодовом режиме, основанный на применении многоканального ДОЭ в качестве корреляционного фильтра. Элементы матрицы определяются в два этапа с помощью передачи тестирующих сигналов по модовым каналам: для каждого столбца матрицы определяются амплитуды элементов и их относительные фазы, затем – разности фаз между столбцами. Входные и выходные ПМ находятся как решения соответствующих уравнений на собственные значения, составленных с использованием полученной матрицы распространения. Базис ПМ, представленный в пространстве

Джонса или Стокса, можно применить как для анализа явлений МД и смешения мод ОВ, так и в качестве набора ортогональных несущих для волоконно-оптических телекоммуникаций на основе MDM.

Проведено численное моделирование процесса определения ПМ для ступенчатого FMF длиной 1002,2 м, поддерживающего распространение мод LP 01 , LP ± 11 , LP ± 21е в режиме сильного смешения. Для полученных ПМ свойство сохранения ортогональности при распространении по ОВ подтверждается тем, что в полосе частот шириной от 256,8 МГц до 352,5 МГц (в зависимости от возбуждаемой ПМ) уровень переходного влияния составляет менее –20 дБ.

Исследование проводится при поддержке Министерства образования и науки Российской Федерации в рамках базовой части государственного задания образовательным организациям высшего образования №2014/240.