Метод определения суммарной дисторсии цифровых изображений

Оснащение робототехнических комплексов системами технического зрения обеспечивает существенное расширение их технологических и функциональных возможностей, наделяет их адаптивными возможностями и элементами искусственного интеллекта [1 -2]. Промышленные системы технического зрения широко используются для бесконтактного контроля геометрических размеров, поиска и обнаружения самых разнообразных дефектов продукции бесконтактным способом, позволяют заменить человека на операциях сортировки и отбраковки продукции, полностью автоматизировать контроль сборки деталей в процессе производства, контроль качества упаковки готовой продукции. Системы технического зрения и видеодатчики являются одним из наиболее эффективных инструментов в задачах идентификации и автоматизации учёта продукции в производственном процессе.

В системах технического зрения можно использовать относительно недорогие цифровые камеры. Конечно, такие камеры по точности результатов не в состоянии конкурировать со специальной аппаратурой, используемой в фотограмметрии, но имеется большой круг задач, где они могут успешно применяться.

При реализации любой методики с использованием реальной камеры требуется знание внутренних и внешних параметров калибровки камеры. Паспортные данные таких сведений не содержат.

Одним из значимых внутренних параметров калибровки камеры является дисторсия цифрового изображения, которая в камерах, не предназначенных для измерительных целей, может достигать заметных величин.

Измерению дисторсии изображения посвящено множество работ [3 - 31]. Условно их можно разделить на две группы. Первая группа работ посвящена аттестации оптических систем на предмет дисторсии при расчёте оптических систем и оценке их качества. Вторая группа работ посвящена задаче ка- либровки камеры с целью определения её элементов внутреннего ориентирования (ЭВО), в том числе дисторсии изображения.

В первой группе нормативным документом является стандарт [3], устанавливающий два метода измерения дисторсии съёмочных объективов, один – для измерения дисторсии на оптической скамье для предмета, расположенного в бесконечности, и второй – для измерения дисторсии объективов, рассчитанных для работы с конечного расстояния.

При аттестации и юстировке объективов на предмет дисторсии важно разделение дисторсии на центрированную и нецентрированную и аппроксимация дисторсии полиномами различных видов. В большинстве случаев рассматривается математический аппарат обработки измерений координат изображений тестовых марок, и расчёт коэффициентов глобальной аппроксимации дисторсии по полиномам Цернике, известным в оптике как базис разложения волновых аберраций. Например, в [4] предусмотрено получение до 98 коэффициентов глобального разложения волновой аберрации, вызванной дисторсией. При разложении волновой аберрации по полиномам Цернике коэффициенты этого разложения, как известно [5], показывают непосредственный вклад аберрации каждого вида в среднеквадратичную волновую аберрацию. Для определения коэффициентов дисторсии по Цернике полученные после измерений составляющие дисторсии трактуются в качестве поперечных аберраций как частные производные волновой аберрации [6].

Известны методы аттестации и юстировки объективов на предмет дисторсии, основанные на измерении искажений квадратной сетки [7] по двум ортогональным осям. Формируемые при этом элементы двух массивов чисел ∆X и ∆Y суммируют в себе расчётную дисторсию и дисторсию, вызванную разными типами погрешностей изготовления и сборки деталей объектива, погрешностями установки объ- ектива при контроле дисторсии, погрешностями измерений. Это обстоятельство не позволяет эффективно использовать массивы ∆X, ∆Y непосредственно для аттестации и юстировки объективов.

В задаче калибровки камеры это обстоятельство наоборот имеет преимущество, так как учитывает суммарную погрешность измерений, независимо от причин их возникновения. Суммарные погрешности искажений изображения многими авторами рассматриваются как систематическая погрешность объектива камеры.

При калибровке камеры в основном используются тестовые объекты, как плоские, так и пространственные. Отмечается, что для определения ЭВО камеры достаточны плоские тестовые объекты. По искажениям изображений тестовых объектов формируются массивы для измерения дисторсии камеры. Сейчас имеется опыт успешных аэросъёмок цифровой камерой и попытки определения параметров цифровых камер [8 - 11].

Известны способы калибровки аэрофотографиче-ской системы с использованием снимков звёзд [12]. Преимущества этого метода – в простоте реализации, в отсутствии необходимости дополнительного оборудования, кроме точных часов. Основным недостатком метода является то, что условия калибровки отличаются от реальной съёмки. Этот факт ограничивает применение метода калибровки по снимкам звёзд.

Более эффективным по сравнению с предыдущими методами выглядит метод калибровки камеры по снимкам специального стенда или испытательного полигона. Данный метод калибровки является наиболее распространённым и легко реализуемым на практике [13 - 19]. Сущность метода – получение калибровочных поправок, учитывающих влияние всех источников систематических искажений, существующих при реальной съёмке. При этом дисторсия может описываться полиномами Эбнера, Якобсона, Грюна, Брауна и т.д. [19].

Использование данного метода калибровки даёт заметное повышение точности измерений. Сложность практической реализации данного метода связана с необходимостью создания дорогостоящих полигонов в различных областях страны. И до настоящего времени не сформулированы оптимальные параметры калибровки камеры по тестовому полигону.

В работах других авторов [19 -27] решение задачи калибровки с необходимой точностью достигалось путём вывода новых математических зависимостей и алгоритмов. Так, в [21] поле дисторсии определяется по изображению плоского тест-объекта и описывается полиномом третьего порядка. Полиномы Цернике использованы в работе [27] для разделения направления децентрировок. Затем с учётом порядка разложения сформированы наборы косинусных и синусных полиномов, что позволяет оценить присутствие в оптической системе ошибок сборки и изготовления.

Также известны работы, в которых описывается аналитический метод самокалибровки [12,28]. Сущ- ность метода состоит в том, что одновременно определяются аналитически поправки к приближённым элементам внешнего ориентирования, координатам точек местности, элементам внутреннего ориентирования и суммарные поправки к координатам точек за влияние всех источников систематических ошибок.

Преимущество данного метода перед методом испытательного полигона состоит в том, что он не требует специального полигона, дополнительных измерений. Поправки в координаты определяются для снимков, по которым строится сеть фототриангуляции, а не по специальным снимкам полигона.

Очевидно, что метод самокалибровки – эффективный способ учёта систематических ошибок снимка, но нет единодушных практических рекомендаций. В работах представлены самые разнообразные полиномы с количеством членов до 20 и со степенью от 1 до 12. В работе [12] отмечается, что нахождение оптимального полинома для описания систематических искажений снимка невозможно, что полином должен формироваться внутри программы при решении конкретной задачи, а не даваться неизменным извне.

Несмотря на многообразие полиномов [12], все они составлены по двум основным идеям. Первая – интегральная систематическая ошибка d x , d y , описываемая полиномом, представлена как сумма членов отдельных систематических искажений (дисторсии, деформации и т. д.).

Вторая идея состоит в том, что представление полиномом интегральной ошибки не связывается с отдельными видами искажений. Интегральная ошибка описывается степенным многочленом.

Этот способ представления дополнительных параметров, вероятно, более правильный, как отмечается в работе [12], так как не связан с определёнными видами искажений. Полиномы же первого вида могут не учесть искажений, которые ещё не изучены или просто не описаны математически.

Другая проблема, с которой сталкиваются исследователи при выборе дополнительных параметров, – это корреляция коэффициентов полинома между собой и другими неизвестными, элементами внешнего ориентирования, координатами точек местности. Это снижает точность фототриангуляции, а иногда сводит на нет попытки увеличения точности за счёт использования самокалибровки. Эта трудность может быть преодолена путём отбраковки сильно коррелированных коэффициентов в процессе уравнивания сети фототриангуляции.

Не сложилось ещё единого мнения по выбору оптимальной длины полинома. Здесь много противоречий. С одной стороны, увеличение количества членов полинома детализирует описание систематических искажений, с другой стороны, ухудшается обусловленность матрицы нормальных уравнений, загружается память ЭВМ. Очевидно, что существуют определённые пределы количества членов полинома, обусловленные исходными материалами, а также памятью ЭВМ. Поэтому длина и вид полинома могут изменяться для различных исходных данных.

Изложенные в работах [6 -28] способы определения оптических аберраций камеры в основном реализованы в виде программных комплексов.

В настоящее время в программных комплексах реализованы два основных способа: полиномиальный, например, работы [19, 21], и способ зон [29]. Для исправления изображения с помощью зон осуществляется поиск формулы преобразования в виде нелинейной функции F от наблюдаемых координат. Предлагается разбивка поля изображения на отдельные клеточные области с предположением линейности закона внутри каждой клетки.

Кроме того, на рынке присутствует больше десятка цифровых фотограмметрических станций (ЦФС) («Дельта» – НПП «Геосистема»; Photomod – компания «Ракурс»; «ЦФС Талка», «Талка ГИС», «Талка КПК» – компания «Талка» и ряд других). Каждая из данных программ обладает своими достоинствами и недостатками.

Область применения ЦФС – фотограмметрия, где используются очень дорогие и точные камеры для формирования изображений, в частности, это космические изображения, предназначены они в основном для картографических работ и обеспечивают возможности GPS-навигатора [30].

Наиболее близким по назначению для нашей работы является программное обеспечение PTLens [31]. Оно предназначено для исправления искажений оптики цифровых камер. Чтобы исправить искажение, программа считывает EXIF-информацию из JPEG-файла, находит ближайшие соответствия в базе данных калибровок камер и автоматически исправляет искажения. Результаты использования программы при корректировке контура цифрового изображения квадратной сетки показали, что программа довольно точно исправляет искажения отдельных линий сетки, но неточно определяет местоположение линии на изображении. Поэтому программа PTLens, предназначенная в основном для корректировки изображений архитектурных сооружений, не приемлема для калибровки камеры.

Таким образом, нужно отметить, что в задачах аттестации и юстировки объективов важно разделение дисторсии на центрированную и нецентриро-ванную, определение причин их возникновения. В задаче же калибровки камеры при определении её внутренних параметров необходимо учитывать суммарную дисторсию, вызванную разными типами погрешностей изготовления и сборки деталей объектива, погрешностями установки объектива при контроле дисторсии, погрешностями измерений, погрешностями установки ПЗС-матрицы камеры. При этом суммарные погрешности искажений изображения надо рассматривать как систематическую погрешность объектива камеры.

Дисторсия изображений

Целью данной работы является разработка метода определения суммарной дисторсии цифровых изображений независимо от причин их возникновения, с дальнейшим исследованием зависимостей дисторсии от фокусного расстояния камеры, расстояния от камеры до исследуемого объекта.

Дисторсия характерна тем, что её величина нелинейно зависит от величины предмета, и приводит к искажению прямых линий, не проходящих через ось [32-35]. При этом квадратный предмет изображается в виде подушки при положительной дисторсии и в виде бочки при отрицательной дисторсии.

Для вычисления дисторсии необходимо определить точку идеального изображения, в которой должно находиться изображение по законам гауссовой оптики. Если кроме дисторсии нет других аберраций, то точка А трёхмерного пространства изображается в виде точки А '( x ', y '), не совпадающей с точкой идеального изображения А '₀ ( x '₀, y '₀) (рис. 1).

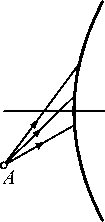
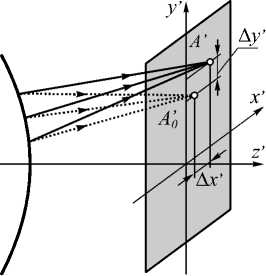
Рис. 1. Дисторсия

Тогда отклонения координат точки А ' – точки пересечения реального луча с плоскостью изображения – от координат точки А ' 0 идеального изображения и есть дисторсия А х ', А у ' соответственно по осям x ' и y ' [32]:

А х ' = х ' 0 - х ', А у ' = у ' о - у '.

Величина дисторсии различна для разных точек поля изображения и является функцией от реальных координат точек изображения x p , y p :

^{А х} ' = ^{А х} '( ^х р , У р ), ^А у ' = ^А у'(^х р , У р ).

Допустимая относительная дисторсия (т.е. дисторсия, при которой нет ощущения, что изображение искажено) около 5-10%. Величина максимально допустимой дисторсии в оптических системах зависит от области их применения. Например, в оптической литографии допуск на абсолютную дисторсию не должен превышать 20 нм [32]. В фотограмметрии погрешность измерений не должна превышать 1 мм. Недорогие цифровые камеры со значительной дисторсией не предназначены для измерений, потому для них нет требований по погрешностям измерений. Тем не менее, в системах технического зрения довольно широко стали использовать неметрические камеры, и известны методы калибровки камер, позволяющие значительно уменьшить дисторсию до 0,3 - 1 пикселя.

Общее описание метода

В приосевой, так называемой параксиальной области оптическая система близка к идеальной. Поэтому в центральной области реального изображения искажения близки к нулю. В этой области точка изображается точкой, прямая линия – прямой. На основе анализа структуры центральной области реального изображения возможно формирование идеального изображения объекта.

В нашей работе определение суммарной дисторсии цифровых изображений основано на измерении искажений квадратной сетки (далее в тексте просто сетки) по двум ортогональным осям.

Сформированные при этом массивы чисел Δ x ', Δ y ' позволяют разработать математическую модель нелинейной зависимости дисторсии от реальных координат узловых точек изображения сетки. Алгоритм решения задачи следующий:

– восстановление контура реального изображения сетки;

– создание идеального изображения сетки;

– определение отклонений узловых точек сетки на реальном изображении от соответствующих точек на её идеальном изображении и построение векторной диаграммы дисторсии изображения;

• -    представление функций А х ', А у ' дисторсии в матричной форме;

  – нелинейный регрессионный анализ аппроксимируемых функций методом наименьших квадратов, подбор вида функции, достоверно описывающей характер изменения дисторсии;

• -    вычисление значений функций А х ', А у ' в точках, отличных от узловых, т.е. решение задачи интерполяции;

  – корректировка реального изображения детали с учётом дисторсии и восстановление плоского контура детали.

Создание идеального изображения сетки

Реальный контур сетки представляет собой линии опредёленной толщины, причём горизонтальные линии сетки имеют верхнюю и нижнюю, вертикальные – левую и правую границы. Восстановление граничных линий сетки выполняется сравнением яркостей пикселей изображения с выбранным значением порога бинаризации.

Далее определяются осевые линии между соответствующими граничными линиями и на пересечении вертикальных и горизонтальных осевых линий определяются узловые точки сетки.

Для восстановления контура реального изображения сетки использованы алгоритмы обработки изображений [34], на основе которых разработана программа в среде Delphi.

Контур изображения сетки в его центральной области зависит от взаимного расположения плоскостей изображения и предмета. Если плоскости параллельны, то перспективные искажения на изображении отсутствуют. Изображение будет представлять собой в общем случае прямоугольную сетку (если коэффици- енты масштабирования разные по осям x' и y'). Тогда по размерам прямоугольной сетки довольно легко сформировать идеальное изображение сетки.

Если плоскости не параллельны, то проявляются перспективные искажения. Центральная часть реального изображения будет представлять собой четырёхугольники с перспективными искажениями сторон. В этом случае для формирования идеального изображения сетки можно воспользоваться точками схода противоположных сторон четырёхугольника и гармоническими свойствами полного четырёхугольника [36].

Векторная диаграмма дисторсии изображения

На рис. 2 приведена векторная диаграмма дисторсии изображения, которая представляет собой совокупность векторов из узловых точек реального изображения в соответствующую ей узловую точку на идеальном изображении сетки. Как видно из рисунка, направления и модули векторов погрешностей различны для разных точек поля, причём характер изменения нелинейный.

Рис. 2. Векторная диаграмма дисторсии изображения

В матричной форме функции поперечной аберрации X, Y будут иметь вид:

X = [ ху ] , Y = [ Уу ] ,

где x ij , y ij – элементы матриц, представляющие величины погрешности в ij узловой точке сетки. Размер прямоугольной матрицы - m х n , где m , n - соответственно количество горизонтальных и вертикальных линий сетки.

Для практического использования функции, представленной в матричной форме (3), необходимо выполнить аппроксимацию функций А х ', А у ', зависящих от координат узловых точек реального изображения сетки. Как правило, регрессионный анализ данных производится методом наименьших квадратов [37].

Нелинейный регрессионный анализ исследуемой зависимости

Классические методы аппроксимации и регрессии функции реализованы во всех современных матема- тических системах (MathCAD, MatLAB, Mathematica, STATISTICA и пр.), которые имеют в своём составе универсальный аппарат выполнения таких операций, и дают пользователю возможность реализации достаточно сложных практических задач по обработке данных. В работе для оценивания параметров регрессии использован программный модуль «Нелинейное оценивание системы STATISTICA», который оставляет за пользователем выбор характера зависимости, что немаловажно для подбора наиболее оптимального вида функции [38 -40]. Для исследуемого процесса в качестве оптимальной функции был подобран полином третьего порядка:

z = a 0 + a 1 x + a 2 y + a 3 x ² + a 4 y ² + a 5 xy + 2  233

+ a 5 x y + a 5 xy + a 5 x + a 5 y .

Дальнейшее увеличение степени полинома не дало ощутимого эффекта в повышении точности обработки данных.

Корректировка изображения

Корректировка изображения предмета заключается в переопределении координат точек контура реального изображения предмета и последующей за ним аппроксимации массива переопределённых точек для восстановления контура предмета. Для определения искажения координат точек изображения предмета решается задача интерполяции, т.е. вычисление значений функций A x ', A y ' в точках, отличных от узловых точек сетки, но принадлежащих контуру изображения предмета. Координаты точек контура скорректированного изображения предмета определяются по формуле:

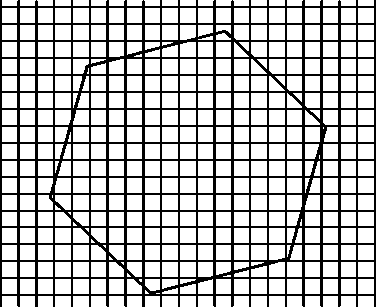
Рис. 3. Объекты исследований

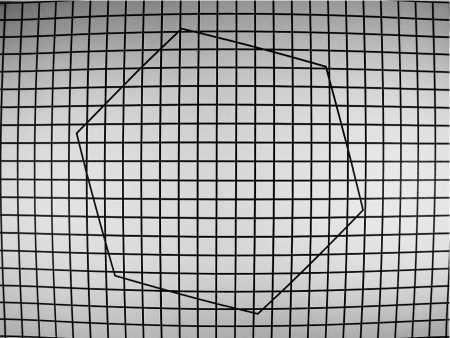
Полутоновое цифровое изображение сформировано в формате *.jpeg. Плоскости изображения и предмета параллельны. На изображении наблюдается отрицательная дисторсия (рис. 4).

x ' 0 = x ' +A x ', y ' o = y ' +A y '.

Экспериментальные исследования

Для экспериментальных исследований применялась система технического зрения, в составе которой использована камера марки Sony DSC-H50. Были проведены несколько серий экспериментов, в которых варьировались размеры сетки, фокусное расстояние и разрешение камеры, расстояние от камеры до сетки. В ходе экспериментов выявлено, что дисторсия цифрового изображения значимо зависит от величины фокусного расстояния и незначимо – от расстояния до предмета. Полученные результаты позволяют оптимизировать процесс формирования цифрового изображения и при необходимости переопределить координаты точек контура изображения. Более подробно результаты изменения дисторсии от условий съёмки будут изложены в другой статье.

В данной же работе важно принципиальное подтверждение результатами экспериментов корректности разработанного метода в целом. Результативность метода оценивается на примере обработки изображений объектов, приведённых на рис. 3: сетки с расстоянием в 10 мм между линиями и правильного шестиугольника с длиной стороны 80 мм.

Рис. 4. Реальное изображение исследуемых объектов

По цифровому изображению вначале восстанавливается контур реального изображения, затем создаётся идеальное изображение сетки. По отклонениям координат соответствующих узловых точек реального и идеального изображений формируются два массива исходных данных X, Y в матричной форме.

Аппроксимация экспериментальных данных полиномом третьей степени показала довольно высокую точность, величина достоверности R ² =0,98–0,99. График аппроксимирующей функции A x ' представлен на рис. 5.

Используемый в работе аппроксимирующий полином третьей степени не накладывает ограничения на линейное или угловое поле зрения тестируемого объектива.

В табл. 1 приведены результаты расчёта координат вершин изображения шестиугольника в пикселях.

На рис. 6 приведены контуры шестиугольника до и после корректировки с учётом суммарной дисторсии изображения на фоне реального и идеального контуров сетки. Внутренний контур (пунктирная линия) – контур изображения шестиугольника до корректировки, причём стороны шестиугольника имеют отклонения от прямых линий. Наружный контур (сплошная линия) – контур после корректировки представлен линейными сегментами.

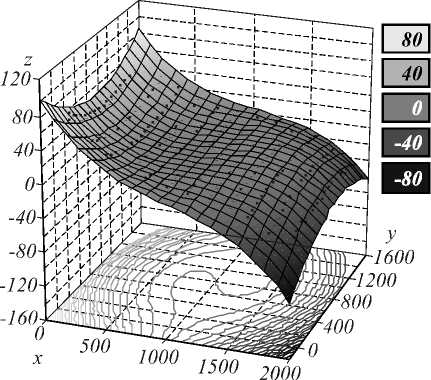
Рис. 5. График аппроксимирующей функции ∆ x' Таблица 1. Результаты корректировки положений вершин шестиугольника в пикселях

№ в е р 1	Реальные координаты		Погрешности		Скорректированные координаты
	x ' 829,2	У ' 1407,7	A x ' 5,23	A y ' -11,87	X ' о 823,97	У ' о 1419,57
2	1484,6	1234,5	-3,69	-5,83	1488,25	1240,28
3	1653,7	582,9	-11,17	5,46	1664,82	577,40
4	1173,5	110,4	-5,14	18,10	1178,60	92,30
5	524,9	284,3	8,85	12,87	516,01	271,44
6	350,2	930,1	12,88	-4,28	337,32	934,36

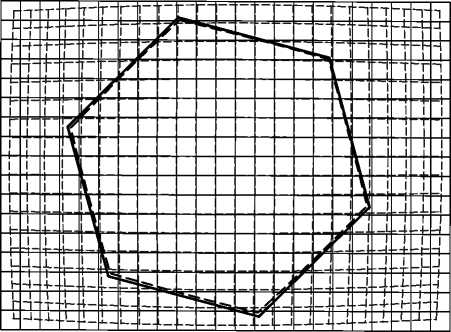
Рис. 6. Контуры шестиугольника до и после корректировки

Результаты расчёта длин сторон шестиугольника до и после корректировки с учётом суммарной дисторсии цифрового изображения в мм приведены в табл. 2.

Из табл. 2 видно, что при восстановлении контура правильного шестиугольника по реальному изображению максимальная погрешность при определении длин сторон составляет ∼ 2,07 мм, после корректировки изображения она уменьшается до ∼ 0,10 мм.

Это свидетельствует о значительном повышении точности восстановления контура шестиугольника после корректировки изображения.

Таблица 2. Результаты расчёта длин сторон шестиугольника в мм

№	Длина стороны шестиугольника, мм
	до корректировки	после корректировки
1	78,91	80,09
2	78,42	79,91
3	78,44	79,98
4	78,17	79,90
5	77,93	79,98
6	78,77	80,02

Заключение

В задаче калибровки камеры при определении её внутренних параметров необходимо учитывать суммарную дисторсию, вызванную разными типами погрешностей изготовления и сборки деталей объектива, погрешностями установки объектива при контроле дисторсии, погрешностями измерений, погрешностями установки ПЗС матрицы камеры. При этом суммарные погрешности искажений изображения надо рассматривать как систематическую погрешность объектива камеры.

Использование квадратной сетки в качестве тестового объекта по сравнению с другими объектами (геометрическими фигурами) имеет большое преимущество, так как более полно иллюстрирует нелинейный характер погрешностей оптических аберраций по всему полю изображения. Уменьшая расстояние между линиями сетки, можно увеличить точность аппроксимации функции погрешностей ∆ x ', ∆ y '.

Создание идеального изображения по реальному изображению тестового объекта позволяет формировать статистические данные для аппроксимации функций погрешностей ∆ x ', ∆ y '.

Для разработки математической модели зависимости погрешностей оптических аберраций от координат узловых точек изображения можно использовать математические системы, имеющие в своём составе универсальный аппарат для решения задач аппроксимации и регрессионного анализа.

Использованный в работе модуль «Нелинейное оценивание системы STATISTICA» показал довольно высокие результаты аппроксимации исследуемой функции полиномом третьего порядка. Величина достоверности аппроксимации R ² =0,98–0,99.

Результаты исследований свидетельствуют о значительном увеличении точности восстановления контуров плоских деталей после корректировки изображения с учётом дисторсии объектива камеры.

Проблема повышения точности восстановления контура исследуемых объектов имеет важное прикладное значение. Например, позволит увеличить точность калибровки систем технического зрения, что немаловажно для интеллектуальных робототехнических комплексов, особенно при решении измерительных задач.

Рассматриваемая задача важна также и для фундаментальных исследований при решении задач сегментации изображений и распознавания образов.

Работа выполнена при поддержке Министерства образования и науки в рамках НИР «Исследование геометрических вопросов интеллектуальных робототехнических комплексов» по Единому заказ-наря-ду, научный руководитель д.т.н., проф., проректор Восточно-Сибирского государственного технологического университета Найханов В.В.