Метод определения вектора спектральных коэффициентов по критерию отношения правдоподобия

Радиоприемная аппаратура спутниковых радионавигационных систем, как и любая другая радиоаппаратура, подвержена воздействию радиопомех естественного и искусственного происхождения. Исследованию направления повышения защиты от радиопомех посвящено множество работ как в отечественной, так и в зарубежной печати. Для реальных условий в последние несколько десятилетий специалистами разных стран разработано множество методов и устройств адаптации к сигнально-помеховой обстановке. Однако накопленные к настоящему времени достижения теории в существующих средствах навигации реализованы далеко не полностью. При достаточно большом разнообразии практически используемых систем защиты большинство из них по структуре и (или) параметрам отличаются от теоретически оптимальных для соответствующих условий. К настоящему времени в радиолокации и навигации с появлением и бурным развитием цифровой элементной базы (программируемых логических интегральных схем, сигнальных процессоров и др.) положение радикально изменилось. Появилась реальная возможность создавать не только надежные, высокоточные, экономичные и малогабаритные цифровые эквиваленты существующих аналоговых систем защиты от помех, но и принципиально новые системы с теоретически существенно более высокой эффективностью.

Наиболее перспективными в настоящее время признаются методы борьбы с помехами на основе пространственной селекции, обеспечиваемой при помощи многоэлементных фазированных антенных решеток (ФАР) [1; 2].

Пространственная селекция сигналов и активных помех основана на использовании отличий в угловых направлениях их воздействия на приемную аппаратуру. В результате пространственной селекции обеспечивается защита от активных помех, действующих по боковым лепесткам диаграммы направленности антенны (ДНА).

ФАР с цифровой реализацией ДНА обеспечивает ее формирование с нулями в направлении помехи и максимумами в направлении на навигационный космический аппарат (НКА). Поскольку весовые коэффициенты для формирования ДНА рассчитываются в программной части, имеется возможность применения различных алгоритмов определения коэффициентов и, соответственно, ДНА в зависимости от поставленной задачи и условий функционирования [3].

Формирование максимумов ДНА в направлении на источник сигнала повышает отношение сиг-нал/помеха, что повышает помехоустойчивость, а общий рост чувствительности обеспечивает прием НКА в сложных условиях, например, в лесу.

В ФАР можно сравнительно просто реализовать специальные виды амплитудно-фазового распределения (АФР) в раскрыве и применять различные методы обработки сигналов, принятых отдельными излучателями антенны. Это позволяет получать низкие уровни боковых лепестков ДНА, извлекать больше информации из приходящих к антенне радиоволн от различных источников, использовать адаптивные алгоритмы оптимальной пространственно-временной фильтрации сигналов на фоне помех, что в целом улучшает характеристики навигационной аппаратуры потребителя.

Наиболее сложной операцией оптимального многоканального обнаружителя является оценка корреляционной матрицы помех, ее обращение и вычисление весового вектора, но с помощью схемы M -элементной ФАР этот процесс можно реализовать (см. рисунок). Вместе с тем именно обратная корреляционная матрица помех содержит всю информацию об угловых положениях источников помех и излучаемой ими спектральной плотности мощности помехи.

Рассмотрим вычисление весового вектора на основе критерия максимума правдоподобия.

Принятый сигнал в общем случае описывается векторной функцией, учитывающей его значения во времени и пространстве.

Помеховые колебания воздействуют в каждом из каналов дискретной приемной аппаратуры, поэтому их будем описывать вектором столбцом:

n ( t ) = || n 1 ( t ), n 2 ( t ), n з ( t ). П м ( t )||^T, (1)

где М - число элементов приемной аппаратуры.

При выделении полезного сигнала на фоне помех используются различия между ними. Математически эти различия лучше учитывать зависимостью сигналов и помех от параметров, которые могут быть пространственными, временными и частотными.

С учетом сказанного, принимаемое колебание, в общем случае, представим в виде выражения

у ( t ) = x ( t , а , в ) + n ( t , v ), (2)

где x(t, а, в) — вектор принимаемого полезного сигнала с параметрами а и в; а - вектор информативных параметров (фаза, время задержки, частота Доплера и т. д); в - вектор неинформативных параметров, вызванных флюктуациями сигнала; n(t, v) - вектор помеховых колебаний; v - вектор параметров помехи.

Относительно помехи будем полагать, что она представляет собой векторный случайный стационарный процесс.

Нормальный закон распределения помеховых колебаний в большинстве случаев физически оправдан, поскольку в сравнительно узкополосных частотных трактах приемников помеха нормализуется.

Тогда можно записать:

Рп(у) = ' exp(-у2/2g2), (3) V 2nG где о2 - дисперсия помехи.

Полагаем, что сигнал и помеха воздействуют на вход многоканальной М -элементной ФАР, расположенной в одном или нескольких пунктах приема. Снимаемая с выходов М -элементной ФАР совокупность напряжений описывается функцией времени у 1 ( t ), у ₂( t ),.... у М t ) и образуют вектор-столбец у ( t ) = || у 1 ( t ), у 2 ( t ), у з ( t ). у М t )||^T. При этом одноканальный прием ( М = 1) рассматривается как частный случай многоканального.

Дискретизацию принимаемых колебаний, в том числе и помеховых, можно производить на радио- и видеочастоте.

Дискретизация на радиочастоте обычно осуществляется с целью упрощения закона распределения помехи. В этом смысле такая дискретизация представляет собой своеобразный математический прием, облегчающей задачу синтеза аналоговых устройств обработки. При пониженной радиочастоте эта дискретизация имеет также целевое назначение при синтезе устройств дискретной (цифровой) обработки.

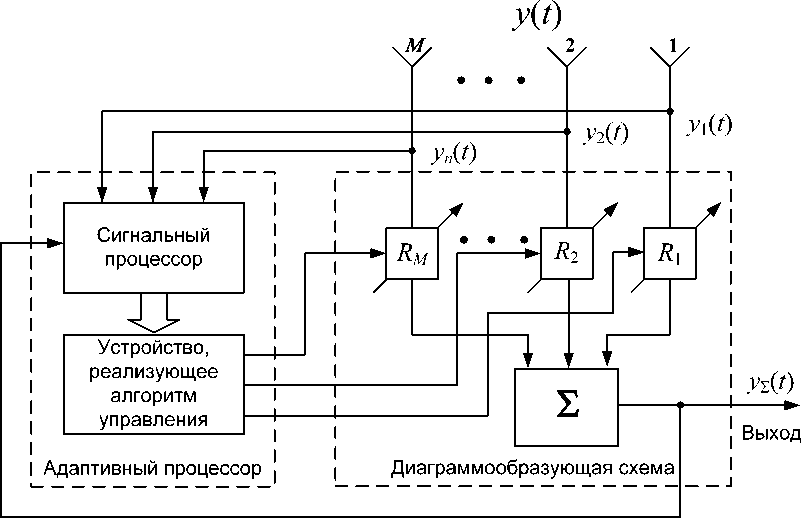
Схема M -элементной ФАР

Особенностью дискретизации на радиочастоте f₀ является относительно малый интервал дискретизации A t , равный примерно половине периода радиочастотного заполнения T ₀ = 1/ f , т. е. A t ~ 1/2 f₀ = T ₀ /2. Дискретные значения радиопомехи y i являются случайными числами, которые удобно представить в виде вектора столбца у = || у ( i A t )|| = || у ( i )||, i = 1, L , где L определяет длину интервала наблюдения Т , а именно: L = T / A t .

В случае многоканального приема вектор принимаемых колебаний записывается в следующем виде: У = || y i ( t )|| = || y k ||, элементами вектора являются значение функции y i ( t ) в дискретные моменты времени t k = k A t , к = 1, L . Общее количество дискрет составит m = ML . Пронумеровав эти дискреты от 1 до m , принимаемому колебанию ФАР будет соответствовать многомерная плотность распределения, представленная следующим выражением:

Р п ( УУ * ) = (4 п ) ^- m |Ф ^{- 1} 1 exp( - У * ^Т Ф ^{- 1} У /2),     (4)

где

У = || У 11, l = 1, m Ф = ^ ik || = м|| уУ_c */2||.      (5)

Необходимую для расчета отношения правдоподобия условную плотность вероятности Р сп ( УУ * ) можно получить по известной плотности вероятности Р п ( УУ * ). При наличии сигнала выборка У характеризуется ненулевым математическим ожиданием:

M ( У) = M [ X (а)] + M [ n ( v )] = M [ X (а)] = X (а).

В этом случае каждая дискрета y i выборки У получает приращение x i (а), а само распределение Р сп ( УУ ''*) смещается на величину математического ожидания X (а).

В результате имеем

Р сп ( УУ ) = Р п [ У - X ( а ), У - X ( а )].      (7)

Составляя логарифм отношения правдоподобия ln l = ln[Рсп (УУ*)/ Рп (УУ*) и подставляя в него (4) и (6) получаем ln l(а) = -[У - X(а)]*T Ф-1[У - X(а)] / 2 +

+ У^т Ф ^{- 1} У /2 = У^т Ф ^{- 1} X ( а )/2 +         (8)

+ X ( а ) ^T Ф ^{- 1} У /2 - X ( а ) ^T Ф ^{- 1} X ( а )/2.

В этом выражении первые два слагаемые образуют сумму комплексно-сопряженных величин. После транспонирования и комплексного сопряжения первого слагаемого последнее приводится к виду X ( а ) * ^T Ф ^{- 1} У /2. При этом было учтено свойство эр-митовости обратной матрицы Ф ^{- 1} , а именно (Ф ^{- 1} ) * ^T = Ф ^{- 1} . В результате сумма первых двух слагаемых (8) будет равна

Z = Re Z ( а ),                     (9)

где

Z ( а ) = Z = X ( а ) ^T Ф ^{- 1} У = У^т (Ф ^{- 1} ) X ( а ).    (10)

Вводя обозначение q 2 (а) = X (а)*T Ф-1 X (а)/2, соотношение (8) окончательно можно записать в виде ln l (а) = Z(а) - q 2(а)/2.

Первое слагаемое в (12) представляет собой реальную часть комплексной весовой суммы:

Z ( а ) = £ У (Ф ^{- 1}) * k X k ( a ),

• i , к

зависящей от дискреты принимаемого колебания у . Параметр q ²( а ) в (12) по своей природе является чисто вещественным и непосредственно от принимаемой реализации не зависит. Он пропорционален энергии полезного сигнала на входе устройства обработки.

Из сказанного следует, что отношение правдоподобия и его логарифм в первую очередь определяется весовой суммой Z = Re Z ( а ), вычисление которой определяет первый и главный этап обработки принимаемого колебания у . По весовой сумме Z ( a ) вычисляются те существенные операции, которые необходимы для извлечения из принимаемой реализации у всей информации о параметрах принятого сигнала. Поэтому Z ( а ) наряду с ln l ( а ) также является достаточной статистикой. Вычисление комплексной весовой суммы предусматривает предварительное формирование весового вектора:

R ( а ) = Ф ^{- 1} X ( а ). (14) с последующим образованием m -элементной весовой суммы

Z ( а ) = У T R * ( а ) = ^ У R * . (15) i

Данное выражение является откликом адаптивной ФАР. Если рассматривать другие критерии эффективности, такие как отношение сигнал-шум, минимальной средней квадратической ошибки, минимум дисперсии шума и другие, то полученные результаты по поиску оптимального весового вектора отличаются лишь постоянным множителем.

Таким образом, получено аналитическое выражение для вычисления весового вектора ФАР, а тот факт, что все решения для оптимального весового вектора в адаптивных ФАР при использовании различных критериев эффективности сводятся (с точностью до постоянного множителя) к винеровскому решению, выбор критерия эффективности принципиального значения не имеет. Более важным является выбор алгоритма управления, предназначенного для постройки ДНА, поскольку он непосредственно влияет на скорость переходного процесса и на сложность технической реализации системы в целом.