Метод определения весов показателей при расчете рейтинга

Рейтинг (сравнительная численная оценка определенного множества объектов) часто используется при подведении итогов деятельности организаций, коллективов и отдельных лиц. Такая оценка обычно рассчитывается на основе ряда контрольных показателей посредством подсуммировки их значений с определенными весовыми коэффициентами. Выбор этих коэффициентов в силу существенной разнородности показателей и ряда других трудноформализуе-мых обстоятельств чаще всего предоставляется экспертам, что может приводить к разногласиям между участниками конкурса или соревнования и не всегда гарантирует объективный результат. Однако в случаях сопоставимых контрольных показателей, например, при подведении итогов соревнований по программированию, в которых контрольные показатели определяются множеством решенных задач, имеется возможность более обоснованного расчета рейтинга. В работе представлена попытка формализации и решения указанной задачи.

ПОСТАНОВКА ЗАДАЧИ

Введем необходимые обозначения. Назовем участниками тестирования сравниваемые объекты или субъекты, их множество обозначим M ( m = | M |). Множество показателей обозначим N ( n = | N |) и будем считать, что известны a_ij – численные значения результатов тестирования каждого объекта i ∈ M по каждому из показателей j ∈ N .

Например, при подведении итогов соревнований по программированию a_ij = 1, если задача с индексом j ∈ N решена участником i ∈ M , и a_ij = 0 иначе. Таким образом, результаты тестирования формализуются в виде числовой, в данном случае бинарной матрицы, итоги тестирования определяются значениями ее элементов. Ограничимся именно такими матрицами.

Цель исследования заключается в поиске оценок значений x_i – искомых рейтингов участников i ∈ M . Строки и столбцы матрицы находятся в определенном отношении двойственности, в силу симметричности исходных условий. Введем также y_j – неизвестные оценки весовых показателей j ∈ N .

Тогда расчет рейтингов заключается в поиске T – способа сопоставления пары числовых векторов x [ M ] ≥ 0 и y [ N ] ≥ 0 произвольной числовой матрице a [ M ; N ]

T ; a [ M ; N ] → ( x [ M ]; y [ N ]).

Очевидно, отображение T не может быть установлено однозначно. В частности, если M = N = 1…m и aij = 1 для всех i ≤ j, то, следуя здравому смыслу, в качестве рейтингов могут использоваться любые монотонно возрастающие числовые последовательности. Поэтому для построения рейтингов введем определен-n ные предположения. Обозначим ki =∑aij – ко-j=1

личество показателей, успешно выполненных участником i е M. lj = ^Taj - суммарный ре-i=1

зультат участников по показателю j е N. Следуя общепринятой логике расчета рейтингов [3], [4], введем следующие предположения.

• •    Исключим из условий задачи неинформативные показатели j е N: l j = 0 или l j = m. Действительно, тест, выполненный каждым или не выполненный ни одним участником, не предоставляет никакой информации о сравнительных результатах участников. Таким образом, будем считать, что 1 < l j < m - 1 для каждого j е N.

• •    Рейтинг участника определяется взвешенной суммой его результатов по показателям m

x = Е ^a j y j .

j= 1

• •    y j > 0, E y j = m . Условие нормировки пре- j= 1

дотвращает чрезмерный рост весов, а неотрица- тельность гарантирует, что результат по показа- телю всегда выгодно улучшить для улучшения рейтинга участника.

y =f ( kl ¹ y   I kJ

где f ( x ) – некоторая монотонно возрастающая функция f :[0 … 1] → [0 …∞ ). Это условие говорит о том, что веса показателей в каком-то смысле обратно пропорциональны сумме оценок участников по показателям. Иными словами, чем лучше выполнен в сумме показатель, тем меньше его вес. Поскольку y_j подчинены условию нормировки, логично накладывать ограничения не на сами y_j , а на их отношения друг к другу.

Можно заметить, что в таком случае требуется предполагать y_j >  0 и k_j >  0, поскольку в противном случае одна из частей равенства будет не определена. Поэтому ужесточим требование к y_j , потребовав y_j >  0. А для того чтобы k_j было строго положительным, введем фиктивного участника, получившего максимальный результат по каждому показателю, таким образом получим k_j ≥ 1.

Конечно, равенство (1) может не выполняться для произвольной функции f . Выведем ограничения на функцию f , позволяющие добиться (1). Будем искать f в классе непрерывно дифференцируемых функций. Пусть m = 3. Будем считать, что k 1 ; k ₂; k 3 е [0 ::да ), поскольку можно считать количество участников сколь угодно большим. Из (1) следует, что

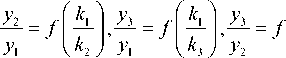
I k ² ) . v k 3 J

Отсюда несложно видеть, что

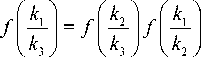
Рассмотрим k 1 = Г Bt "I, k2 = Г 1 "I, k3 = Г At "I для некоторых положительных A и B. Заметим, что в силу непрерывности функции f при t → ∞ выражение (2) примет вид f (B1= f (11 f (B).           (3)

v A J    v A J ^v ’

Выражение (3) верно для всех A и B . Так как f дифференцируема, мы можем продифференцировать (3) по B , получая — / 1 B | = f ( B ) f | | .

A v A J         v A J

Рассмотрим это выражение при B = 1. Обозначив ¹ = x , получим уравнение

A               xf (x) = f (1) f (x) .

Полагая У (1) некоторой константой C, реша- ем это уравнение, получая решение в виде:

f ( t ) = e^C1 +C 1 , где C 1 - некоторая произвольная константа.

Таким образом, мы доказали

Утверждение 1. Равенство (1) в классе непрерывно дифференцируемых функций достигается тогда и только тогда, когда f ( x ) = Ax + B для некоторых A и B.

Покажем, что в этом утверждении B = 0. Для этого рассмотрим (2) при k ₁ →∞ , в силу непре- k ₂ k ₃

рывности f получим f ( 0 ) = f

f ( 0 ) . Отсюда

либо f (0) = 0 (а тогда очевидно и B = 0), либо

• f ² = 1 для любых k и k . Но в таком случае

I k ₃ J               ²³

мы получаем f ( x ) = const , а стало быть, все y_j равны. В силу условия нормировки мы получаем, что y_j = 1, а рейтинг вырождается в простую сумму результатов участника по показателям.

^y j       k

В случае же когда B = 0, мы получаем    = A ^l .

ylkj

В таком случае, рассматривая эти уравнения при l = 1, получаем yj =A 1 y1 . Добавляя усло-kj вие нормировки, получаем систему уравнений, из которых находятся yj и константа A km yj=A"byx;vjе [1-m ], Е yj=m.

k1

mk -

Решая эту систему, получаем.

Система (4) была рассмотрена при l = 1 и не учитывает все уравнения из (1). Если проверить полученное решение, окажется, что оно не удовлетворяет (1). Стало быть, требуется другой подход.

Заметим, что в силу утверждения 1 разумным выглядит предложение ослабить ограничение (1). Будем вместо функции, в точности удовлетворяющей (1), искать функцию, наиболее точно подходящую под заданное ограничение. Для этого воспользуемся методом наименьших квадратов, заменяя (1) на

У - - f ⁽ v j * 1 1 у I      I kj

Тогда для нахождения y_j требуется решить следующую оптимизационную задачу:

(

У j - f ⁽ v j * 1 1 У ,     I k

m

^ min; У y₎=m;y_j> 0 . (6) j= 1

Задача (6) является классической задачей на условный экстремум, однако попытка применить метод множителей Лагранжа для ее решения оказалась неудачной, поскольку целевая функция является существенно нелинейной и выражения для ее производных оказываются весьма громоздкими. Поэтому для решения задачи (6) будем использовать численные методы. Заметим, что если для какого-то j yj → 0, то всегда существует 1, такая что yl * 0 (в силу условия нормировки и неотрицательности), а в таком случае целевая функция неограниченно воз-y растает за счет отношения l , поэтому можно yj предположить, что задача имеет решение.

Обозначим F ( у ) = У —

У ,

. Заметим,

что F ( λy ) = F ( y ) . Это наблюдение позволяет надеяться на то, что условие нормировки в задаче является несущественным. Для доказательства

рассмотрим задачу без этого условия.

(                   2

у y- - $ ^

* i у, к,

y j

j * i ( У ,

^ min;y j >  0

.

Обозначим N ( у ) = my • Заметим, что

N ( y )

В одну сторону это утверждение уже доказано, в обратную же оно очевидно.

Таким образом, можно сконцентрироваться на исследовании задачи (7). Для решения этой задачи модифицируем метод наискорейшего градиентного спуска [2] следующим образом.

• •    Шаг 0. Положим y_i ⁰ = 1, k= 0 .

• •    Шаг 1. Вычислим v = -V F ( y k )

(- y k       )

• •    Шаг 2. Положим λ=min   ⁱ ,v< 0 . Мо-

• I v.     i )

жет оказаться, что 2 = да , в таком случае положим ее равной некоторой большой константе, определяемой эмпирически.

• •    Шаг 3. Вычислим t^s = argmin ( F ( y + tv ), t е [0... 2 ]. Для вычисления ts можно решить одномерную оптимизационную задачу методом троичного поиска.

• •    Шаг 4. Положим y^k+1 = N ( у + tv ) .

• •    Шаг 5. Если max_i ( y_i^{k +1} – y_i^k ) <  ε, точка y^{k +1} объявляется приближенным решением задачи и алгоритм завершается. В противном случае полагаем k = k + 1 и переходим к шагу 1. В численных расчетах использовалось значение ε = 0,01.

Приведенная выше модификация метода градиентного спуска достаточно быстро сходится на различных тестах при различных видах функции f ( x ).

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Приведем результаты применения предложенного метода на различных тестовых данных. Привести реальные тестовые данные не представляется возможным в силу их значительного размера.

В табл. 1 приведено сравнительное количество итераций метода на одних и тех же тестовых данных в зависимости от вида функции f ( x ).

Таблица 1

определена на всем допустимом множестве как задачи (6), так и задачи (7).

В силу (1) задача (7) не имеет точек строгого локального минимума, поскольку V е F ((1 + е ) у ) = F ( у ). Поэтому решением задачи (7) мы будем называть точку нестрогого локального минимума функции F . В таком случае очевидно утверждение, что если y^* – решение (7), то и N ( y^* ) – решение (7).

Теперь пусть y^* – решение задачи (7). Покажем, что N ( y^* ) – решение задачи (6). Пусть это не так, и существует последовательность y , удовлетворяющая условиям (6), такая что F^k ( y_k ) < F ( y^* ). Но тогда последовательность y_k удовлетворяет условиям (7), а значит N ( y^* ) не является решением (7). Это противоречит доказанному выше. Таким образом доказана

Лемма 1 y^* является решением (7) тогда и только тогда, когда N ( y^* ) является решением (6).

Количество итераций метода при различных f (x)

Вид f (x)	Тест 1 N = M = 3	Тест 2 N = M = 10	Тест 3 N = M = 10	Тест 4 N = 43, M = 11	Тест 5 N = 107, M = 79
f ( x ) = x	3	1	35	2	159
f ( x ) = xx	6	1	6	32	46
f ( x ) = e	12	16	1	1	1
f ( x ) = V x	1	1	8	16	18
f ( x ) = x V x	4	1	1	14	28
f ( x ) = 4fx	1	1	3	4	5
f ( x ) = log( x + 1)	1	1	5	9	11
$ ( x ) = x log( x + 1)	3	1	1	11	59

Табл. 2, 3 отражают результаты работы метода при f ( x ) = x как наиболее интересные. Каждая из этих таблиц состоит из N + 1 строки и M + 1 столбца. В последней строке приведены полученные

рейтинги задач, в последнем столбце – полученные рейтинги участников. Остальная часть таблицы представляет исходные данные – результаты каждого участника по каждой задаче.

В первом тесте (табл. 2) можно заметить, что если участники решают задачи в порядке возрастания сложности, то рейтинг очевидным образом будет больше у участника, решившего больше задач. В тесте (табл. 3) отражено, как решение нетривиальных задач может значительно поднять рейтинг участника.

ЗАКЛЮЧЕНИЕ

Проведены численные эксперименты с различными видами функции f ( x ). Наиболее интересными, на наш взгляд, оказались результаты при линейной f ( x ) , которые приведены в таблицах. Предложенный метод расчета рейтинга достаточно быстро сходится на тестовых данных, что позволяет использовать его на практике. Остается открытым вопрос о единственности локального минимума функции F , а также об условиях, которые требуется наложить на функцию f , чтобы приведенный метод гарантированно сходился.

Таблица 2

Тест с верхнетреугольной матрицей результатов

1	1	1	3
0	1	1	1,61
0	0	1	0,69
1,38	0,92	0,69

Таблица 3

Тест, в котором один из участников (последний) решил две задачи, не решенные более никем

1	1	1	1	1	1	0	0	0	0	3,56
1	1	1	1	0	0	0	0	0	0	1,97
1	0	1	1	1	0	0	0	0	0	1,73
1	0	0	0	0	0	0	0	0	0	0,22
1	0	0	0	1	0	0	0	0	0	0,90
1	0	1	0	0	1	0	0	0	0	1,50
1	0	0	1	0	0	0	0	0	0	0,69
1	0	1	0	0	0	0	0	0	0	0,59
1	0	0	0	0	0	0	0	0	0	0,22
0	0	0	0	0	0	1	1	0	0	2,47
0,22	0,91	0,37	0,47	0,68	0,91	1,24	1,24	1,98	1,98

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

METHOD FOR COMPUTING MEASURES’ WEIGHTS FOR RATING COMPUTATION

The goal of the study is to constrct objective estimates of several participants’ activity based on the results obtained by several quantitative measures. Usually, to construct such estimates weights of measures provided by experts are introduced. This leads to disagreements and does not quarantee objective result. Though in some cases (especially when measures are comparable), we can compute rating on a more reasonable basis. This paper provides a mathematical model for computing objective weights of measures and computing participants’ rating with these weights. The proposed method requires solving of non-linear optimization problem. To solve the problem we used a gradient method, which was modified to meet the requirements of our model. The method was tested on several examples. The experiment helped to illustrate the method’s efficiency and effect of participants’results on measures’ weights. Key words: rating, objective estimates, gradient method