Метод определения входных сигналов бортовых систем ближней радиолокации от объектов сложной формы на основе использования их полигональных и многоточечных моделей
Бесплатный доступ
Рассмотрены вопросы математического моделирования входных сигналов систем ближней радиолокации на основе полигональных и многоточечных моделей объектов локации. Получены аналитические соотношения для определения мощности отраженного от цели сигнала в непрерывном и импульсном режимах излучения. Приведены результаты цифрового моделирования входных сигналов систем ближней радиолокации от типовых аэродинамических целей на основе использования их полигональных и многоточечных моделей
Система ближней радиолокации, многоточечная модель, полигональная модель, аэродинамическая цель
Короткий адрес: https://sciup.org/14967158
IDR: 14967158
Текст научной статьи Метод определения входных сигналов бортовых систем ближней радиолокации от объектов сложной формы на основе использования их полигональных и многоточечных моделей
З начительное расширение условий применения современных систем ближней радиолокации (СБРЛ) приводит к необходимости проведения исследований по уточнению областей срабатывания по сложным аэродинамическим целям [1]. В качестве альтернативы дорогостоящим натурным измерениям характеристик срабатывания СБРЛ в настоящее время широко применяется функциональное полунатурное моделирование, которое позволяет моделировать работу СБРЛ в реальном масштабе времени во всем многообразии условий встречи, в том числе при работе по объектам локации со сложной геометрией поверхности в условиях активных и пассивных помех, воздействий сигналов, отраженных от подстилающих поверхностей.
Современным инструментом, позволяющим эффективно решать сложные задачи всесторонних испытаний как модернизируемых, так и вновь создаваемых перспективных СБРЛ, являются стенды полунатурного моделирования (СПНМ). Имитация процесса электромагнитного взаимодействия СБРЛ с объектами локации должна включать в себя:
-
♦ моделирование отраженного от объекта локации сигнала, формируемого в реальном масштабе времени, с учетом его сложной геометрической формы, взаимной ориентации объекта слежения и носителя СБРЛ и кинематики их скоростного относительного движения;
-
♦ моделирование отраженного сигнала от подстилающей поверхности;
-
♦ моделирование активных и пассивных помех.
В состав СПНМ входят каналы имитации входного сигнала СБРЛ, сигнала активной помехи, сигнала от подстилающей поверхности и измерительный канал. В блоке имитации сигнал, излучаемый СБРЛ, преобразуется в отраженный сигнал путем изменения параметров излучаемого сигнала по законам, определяющим взаимосвязи между излученным сигналом СБРЛ и сигналом, отраженным от реального объекта локации. Канал имитации входного сигнала в СПНМ построен на основе принципов функционального моделирования, т.е. параметры отраженного от цели сигнала вычисляются на ЭВМ в результате использования соответствующей математической модели.
Радиолокационная цель
Поэтому существует необходимость в создании нового математического аппарата, позволяющего проводить расчеты входных сигналов СБРЛ для проведения полунатурных испытаний. В задачах расчета входных сигналов СБРЛ возникает проблема анализа электромагнитных полей, отраженных от объектов сложной геометрической формы. Данная проблема связана с решением задачи дифракции электромагнитной волны на объекте с привлечением довольно сложного и громоздкого математического аппарата как для тел сложной формы, так и для простых объектов ( рис. 1 ).
Следует отметить, что существующие численные методы решения задачи дифракции (метод моментов, метод конечных разностей во временной области) и основанные на них пакеты прикладных САПР имеют следующие особенности практического применения:
-
♦ необходимость использования значительных вычислительных ресурсов при расчетах характеристик отражения объектов большого электрического размера;
-
♦ невозможность непосредственного использования этих методов и программ при проведении полунатурных испытаний СБРЛ.
Поэтому возникает необходимость в исследовании асимптотических методов решения задачи дифракции, основанных на различных упрощениях и допущениях при интегрировании системы уравнений. Асимптотические методы с успехом применяются к анализу вторичного излучения достаточно сложных целей большого электрического размера. В общем случае электрическое поле рассеяния объекта может быть определено на основе интегрирования вторичных источников поля, распределенных на поверхности объекта [2]:
Ёг
1 Г - - О'
Для определения поля вторичного излучения необходимо определить сами источники вторичных волн которые образуются на поверхности объекта при его облучении первичным полем. Эти источники вторичного излучения можно определить различными методами, которые условно разделяют на асимптотические и эвристические.
Для расчета электромагнитных полей рассеяния объектов локации используют методы физической оптики (ФО), физической теории дифракции (ФТД) [3] и метод краевых волн (МКВ). В соответствии с формализацией процесса рассеяния электромагнитных волн на элементах радиолокационной сцены на основе метода ФТД вектор напряженности электрического поля рассеяния этих источников может быть представлен как векторно-когерентная аддитивная композиция трех компонент:
E scat = E 1 + E 2 + E 3 ,
где E1 – вектор напряженности поля рассеяния, который соответствует вкладу в общее рассеянное поле от гладких элементов радиолокационной сцены (в том числе и от подстилающей поверхности), В/м; E2 – вектор напряженности поля рассеяния, который соответствует вкладу от острых кромок элементов сцены, ), В/м; E3 – вектор напряженности поля рассеяния, который соответствует рассеянию при многократных переотражениях электромагнитных волн между
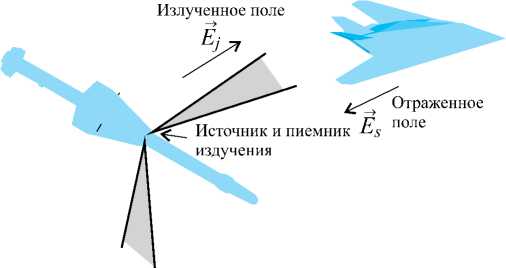
Рис. 1. Схема взаимодействия СБРЛ и радиолокационной цели
элементами сцены (в том числе между элементами объектов и подстилающих поверхностей), В/м.
Общей особенностью первых трех компонент (2) является их аддитивно-интегральная форма представления:
где F – вектор поверхностных источников возбуждения, – источники электромагнитного поля рассеяния на поверхности объекта.
Для оценки полей рассеяния подстилающих поверхностей целесообразно использовать существующие в настоящее время электродинамические методы статистического усреднения электромагнитных полей рассеяния от хаотических неровностей, такие как метод касательной плоскости, метод малых возмущений, метод двухкомпонентной поверхности. При проведении расчетов входных сигналов СБРЛ от объектов локации должна использоваться полигональная модель цели, которая представляет поверхность объекта в виде совокупности плоских треугольников. Наиболее передовым и мощным инструментом 3D-моделирования сложных объектов на сегодняшний день является Pro/Engineer Wildfire 5.0 (Creo), который позволяет синтезировать сеточную модель внешней поверхности объекта максимально точно и эффективно. Создание 3D-моделей целей в Pro/Engineer проводится с использованием инструментов твердотельного и поверхностного моделирования.
В рамках исследований в Pro/Engineer были разработаны твердотельные геометрические и полигональные модели различных аэродинамических целей, в том числе многоцелевой истребитель F-22 Raptor ( рис. 2 ), крылатая ракета Tomahawk BGM-109 ( рис. 3 ), истребитель F-117 ( рис. 4 ) и др. Функционирование СБРЛ осуществляется в ближней зоне локации, когда СБРЛ находится на таком расстоянии до объекта, что критерий дальней зоны не выполняется, а падающая на объект электромагнитная волна имеет в месте его расположения существенно сферический фронт.
Фацетное представление полигональной модели радиолокационной цели позволяет представить сферическую электромагнитную волну вблизи облучаемого участка сцены в
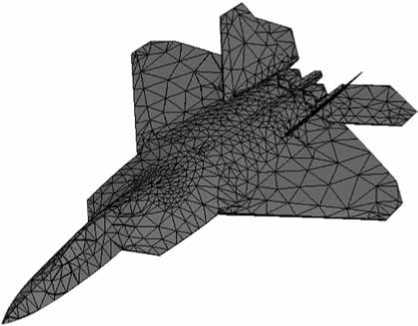
Рис. 2. Полигональная модель истребителя F-22
виде суперпозиции локально плоских волн. При этом пространственная сетка внешней поверхности объекта формируется таким образом, чтобы падающие на элементы полигональной модели электромагнитные волны можно было рассматривать как локально плоские. Для того чтобы падающую на элемент полигональной модели электромагнитную волну считать плоской, его линейный размер должен удовлетворять критерию дальней зоны:
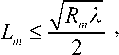
где Lm – характерный линейный размер m -го элемента полигональной модели; Rm – расстояние между фазовым центром антенны СБРЛ и m -м элементом.

Рис. 3. Полигональная модель ракеты «Tomahawk»
В соответствии с формализацией дифракционного электромагнитного поля рассеяния сцены, заданной своей полигональной моделью, величина результирующей напряженности поля рассеяния, принятого в апертуре приемной антенны СБРЛ, представляется в виде суперпозиции полей рассеяния всех элементарных отражателей (ЭО) полигональной модели сцены:
т=0
где m – индекс элементарного отражателя (ЭО); Е$т = Е™,Е0 – величина напряженности электрического поля рассеяния m -го ЭО, принятого в апертуре приемной антенны СБРЛ, В/м; N∑ – общее количество ЭО, принимающих участие в рассеянии электромагнитных волн.
На основе поляризационной модели поля рассеяния объекта, заданного совей полигональной моделью, получено соотношение для расчета величины результирующей напряженности электрического поля рассеяния, принятого в апертуре приемной антенны СБРЛ:
£ y = У Ё -p L sm m=0
РРТ^ X р д £xp(7(£/?^jl-69/jl-^^ . (5) 2я £0 ™Psm RimRm
Результирующее напряжение, возникающее в нагрузке приемной антенны от воздействия цели в ближней зоне локации, определяется следующим образом:
N-”' I2 2
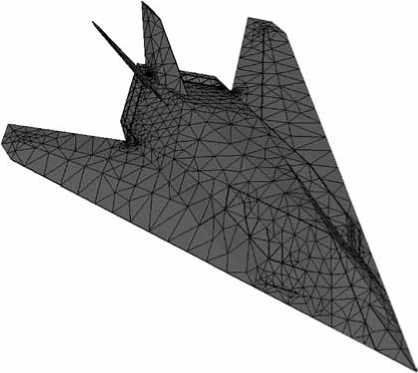
Рис. 4. Полигональная модель истребителя F-117
Ц„р = IL U»-=F 'RV ехр(/И + Ф№; ,(6)
т=о V ОТТ
Is = у F F р ^x*kRi'^ , i mt sm i sm D D m=0 1Vim1Vsm где . – результирующий коэффициент рассеяния объекта, выраженный в [1/м], Psm – комплексный коэффициент отражения ЭО.
Мощность входного сигнала СБРЛ, работающей в непрерывном режиме излучения, будет вычисляться на основе следующего соотношения:
Результирующие составляющие сигналов в антенне импульсной СБРЛ, принятых от всей цели, определяются в результате суммирования отдельных импульсов, принятых в разные интервалы времени tm по всем ЭО цели:

.
",=0 °л+/т — t — i
.
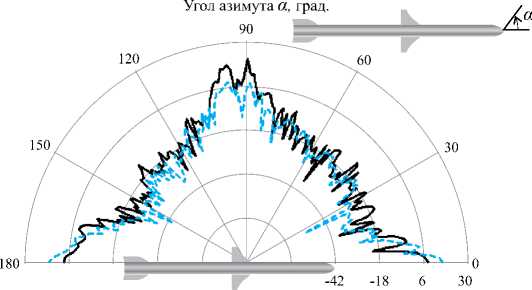
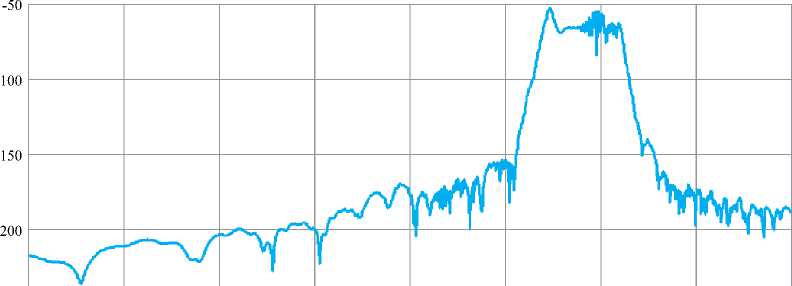
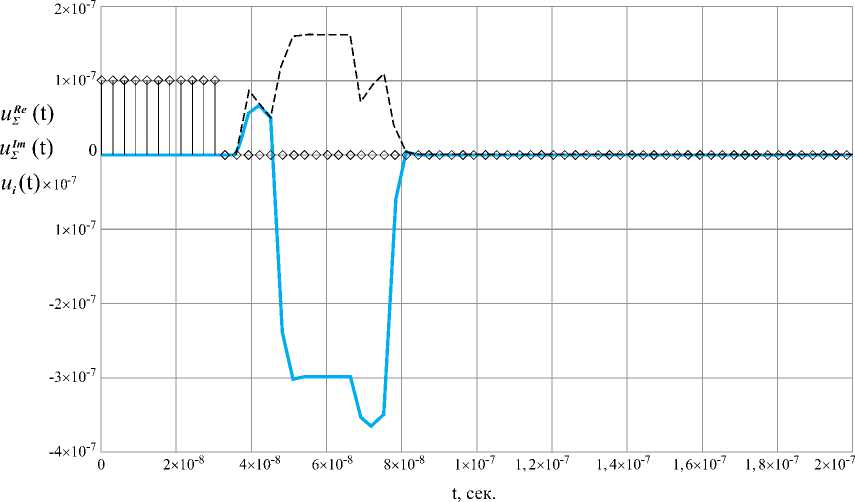
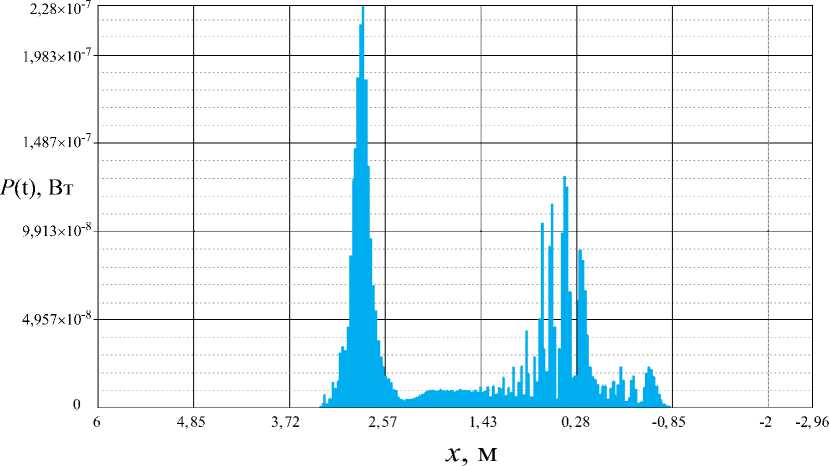
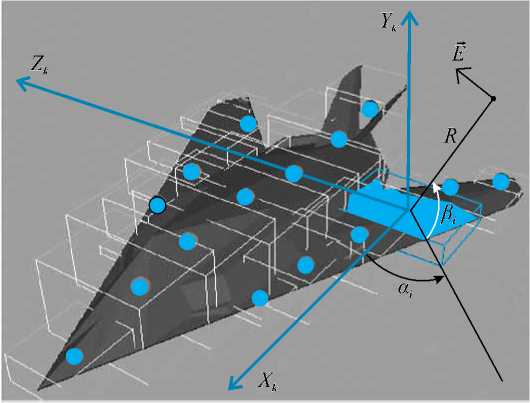
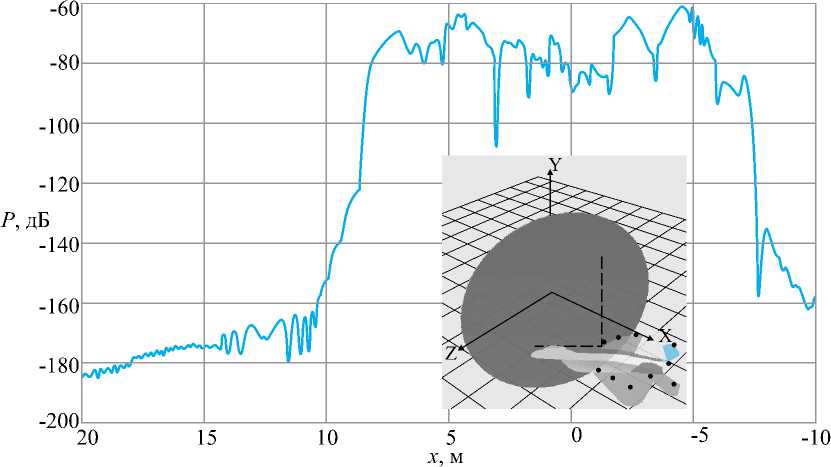
x „ m=0 0, TJ( + ^ < t Модуль комплексной огибающей единичного импульса, отраженного от всей цели с учетом локальных задержек импульсов от отдельных отражателей, имеет следующий вид в единицах мощности: P^ На рис. 5 приведено сопоставление диаграммы обратного рассеяния ракеты «HARM» в дальней и ближней зонах локации (ракета находится на расстоянии R =5 м от антенны), вычисленные на согласованной горизонтальной поляризации. Также на рис. 5 приведена полигональная модель ракеты «HARM». В соответствии с рис. 5 в ближней зоне эффективной площади рассеяния (ЭПР) ракеты незначительно увеличивается по сравнению с ЭПР в дальней зоне в области носовых ракурсов до значения σ = 4,8 м2, а в области хвостовых ракурсов до значения σ = 8,6 м2. При этом в области боковых ракурсов ЭПР в ближней зоне локации уменьшается примерно на 10 дБ по сравнению с ЭПР в дальней зоне и не превышает значения σ = 2,1 м2. В качестве примера были проведены расчеты мощности входного сигнала импульсной СБРЛ ракеты «Гарпун», заданной своей полигональной моделью. Расчет огибающей мощности и квадратурных сигналов для импульсной СБРЛ проводился по формулам (9, 10). Для сравнения был также проведен расчет по формуле (8) для СБРЛ в непрерывном режиме излучения. Параметры СБРЛ, для которой был вычислен отраженный сигнал от цели приведены в [1]. На рис. 6 приведена зависимость мощности сигнала, отраженного от ракеты «Гарпун» при ее пролете вдоль оси x в диапазоне координат условной точки X = {30…-10} м на ЭПР. дБ Рис. 5. Диаграммы обратного рассеяния ракеты «HARM» на согласованной горизонтальной поляризации на длине волны 3 см (сплошная кривая – дальняя зона, штриховая кривая – ближняя зона) промахе r = 5 м. Данный график построен по формуле (8) для случая, когда СБРЛ работает в непрерывном режиме излучения. Как видно из графика, область, существенная для отражения, лежит в диапазоне X={4…-2} м, где значения мощности составляют P={-50...-80} дБ. В качестве примера при расчете отраженного импульса от ракеты «Гарпун» был выбран ракурс наблюдения, при котором условная точка цели находится в x = 5 м, т.е. цель только входит в диаграмму передатчика. Соответственно на рис. 7 приведены огибающие квадратурных сигналов и импульса мощности при заданном ракурсе наблюдения. Как видно из графиков, длительность отраженного от цели импульса составляет величину порядка τотр = 50 нс, т.е. длительность импульса увеличилась на 20 нс по сравнению с зондирующим (τи = 30 нс). Увеличение длительности импульса обусловлено наличием дополнительных временных задержек от ЭО, расположенных на разных дальностях. Величина задержки, на которую увеличивается длительность импульса, составляет Δτ = 2(Rmax – Rmin)/c, где Rmax(min) – максимальная ■250 30 25 20 15 10 5 0 -5 -10 X, M Рис. 6. Зависимость мощности отраженного сигнала от ракеты «Гарпун» от координаты x ее условной точки (СБРЛ в режиме непрерывного излучения) Рис. 7. Отсчеты напряжения квадратурных импульсов от цели «Гарпун» (сплошная линия – действительная часть, штриховая линия – мнимая часть, квадраты – значения огибающей нормированного зондирующего сигнала) (минимальная) дальность от антенны до отдельных участков цели. В связи с тем, что длина ракеты «Гарпун» составляет 2,5 м, величина задержки, вычисленная по указанной выше формуле, соответствует значению, полученному в результате моделирования. Кроме того, на рис. 8 приведены отсчеты огибающей импульсов мощности отраженного сигнала и огибающей импульсов квадратурных сигналов, принятых на траектории пролета цели, относительно ракеты. Из графиков видно, что область, наиболее существенная для отражения импульсного сигнала, находится в пределах X={2,7..-1} м. Полученные результаты расчета входных сигналов СБРЛ от целей могут быть использованы при определении областей срабатывания СБРЛ. Для получения достоверных результатов при расчетах входных сигналов СБРЛ количество треугольников полигональной модели поверхности сложной цели (ракета, самолет) должно составлять N ≈ 105…107. При этом расчет модели на Рис. 8. Отсчеты импульсов мощности, отраженных от ракеты «Гарпун» траектории движения на современных многоядерных процессорах достигает T ≈ 1…10 ч (в зависимости от типа цели и параметров ЭВМ). Поэтому полигональная модель является практически непригодной для оперативной оценки функционирования СБРЛ на СПНМ и расчета его эффективности при большом количестве реализаций траекторных сигналов. При проведении тестирования работы СБРЛ требуется большая статистика по условиям встречи в широком диапазоне их изменения. С этой точки зрения разработка многоточечных моделей с изменяющимися отражающими свойствами более предпочтительна, т.к. определение локальных отражающих участков дает возможность избежать математического описания геометрии цели и соответственно значительно сократить время расчета при неизбежном снижении точности вычислений. По результатам расчетов показано [4], что средняя погрешность расчета по существующей в отрасли модели по сравнению с полигональной моделью не превышает 6 дБ, а погрешность по максимальному значению мощности не превышает 3 дБ. В результате можно утверждать достаточно хорошую степень совпадения результатов расчета по математической модели и феноменологической модели для одной цели, что говорит о пригодности полигональной модели для формирования многоточечной. Многоточечная модель объекта локации формируется на основе математического моделирования в результате расчетов на ЭВМ с использованием полигональной модели цели. При формировании многоточечной модели полигональная модель цели представляется в виде набора проекционных параллелепипедов, каждый из которых ограничивает определенный участок поверхности цели (рис. 9). В результате расчетов каждому m-му параллелепипеду будет соответствовать «блестящая» точка. Многоточечная модель цели представляет собой массив «блестящих» точек, которые будут служить пространственным эквивалентом сложной цели при формировании быстрой модели расчета входных сигналов СБРЛ: Рис. 9. Формирование многоточечной модели цели (F-117) на основе ее полигональной модели (локальная система координат k-го локального отражателя) Pm = {Xm Ym Zm}, m = 1…Nm, где m – номер точки многоточечной модели цели в порядковом списке, Nm = Nпар – общее число точек, равное числу параллелепипедов. На этапе формирования многоточечной модели для каждого параллелепипеда (локальной точки) вычисляется пространственная диаграмма ЭПР в сферической системе координат локального отражателя (Xm, Ym, Zm). Расчет ЭПР осуществляется для углов азимута αi = α0 + iΔα (α0 = 0, αmax = 360°) и углов места βi = β0 + iΔβ (β0 = 0, βmax = 360°) в локальной системе координат отражателя при заданном расстоянии R от антенны до локального отражателя. Расчет проводится по методике, приведенной в [2] для вычисления ЭПР объекта в ближней зоне локации на основе полигональной модели. При вычислении ЭПР каждого отражателя учитывались только те треугольники, которые попадали в область, ограниченную кубом данного отражателя. С учетом перечисленных условий ЭПР локального участка цели, ограниченного проекционным параллелепипедом, в виде суммы комплексных коэффициентов отражения попадающих в параллеле- пипед треугольников: Ч^Р) = 4тг ",,-1 £ Psk к=0 где Psk – комплексный коэффициент отражения k-го тре- угольника, попадающего в пределы m-го параллелепипеда. В результате формирования многоточечной модели для каждого локального отражателя формируется двумерный массив значений ЭПР в локальной системе координат σi,j = (αi, βj). Каждый из массивов ЭПР сохраняется в текстовых файлах, которые являются исходными данными для многоточечной модели цели. При расчете мощности входного сигнала СБРЛ на траектории движения цели используются массивы значений ЭПР и начальной фазы локальных отражателей, рассчитанные на этапе формирования многоточечной модели. В соответствии с представлением цели в виде набора локальных отражателей мощность входного сигнала СБРЛ получим в виде: р=РМ£. (4^)2 уЗк^кРк где Nm – число локальных точек многоточечной модели цели, Рк – комплексный коэффициент отражения локального отражателя. Комплексный коэффициент отражения локального отражателя многоточечной модели определяется из соотношения: А. = ^^ exp ^-z'2 ^ А ^ ’ (14) где σk – ЭПР k-й точки, которая вычисляется за счет интерполяционных соотношений для соседних значений диаграммы ЭПР. В качестве математической модели диаграммы направленности антенны (ДНА) СБРЛ используются данные экспериментальных измерений. В этом случае диаграмма представляется в виде дискретного набора Nf значений Fi в плоскости оси ракеты. Каждому значению ДНА Fi соответствует угол γi, отсчитываемый от оси ракеты. В этом случае значение Рис. 10. Зависимость мощности сигнала, отраженного от истребителя F-22 (многоточечная модель) на траектории движения, от координаты условной точки цели ДНА для произвольного угла γ определяется на основе линейной интерполяции соседних значений: F( У) = F^) + (У - Уд ^^rf^, (15) где γi+1 ≤ γ ≤ γi. В соответствии с соотношением (15) вычисляются значения функции направленности антенны СБРЛ в направлении на m-ю точку Fik = Fi(γk), Fsk = Fs(γk), и подставляются в расчетную формулу мощности входного сигнала (14). В качестве примера результатов расчета входных сигналов СБРЛ на рис. 10 приводятся зависимости мощности входных сигналов СБРЛ от многоточечной модели истребителя F-22. В результате можно сделать следующие выводы. 1 Разработанный метод определения входных сигналов СБРЛ от объектов локации на основе использования поли- 2 Предложенные в работе математические модели отраженных сигналов от объектов локации являются эффективным современным средством оценки их характеристик рассеяния при самых общих условиях локации, что позволяет заменить сложные и дорогостоящие натурные измерения более дешевыми и функционально более гибкими средствами математического моделирования современных САПР. 3 Предложенная в работе многоточечная модель объекта сложной формы является эффективным средством проведения полунатурных испытаний СБРЛ на моделирующем стенде в реальном масштабе времени ■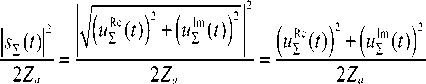

Список литературы Метод определения входных сигналов бортовых систем ближней радиолокации от объектов сложной формы на основе использования их полигональных и многоточечных моделей
- Андрюшин О.Ф., Антонов К.А., Борзов А.Б., Сучков В.Б., Фабричный М.Г. Автоматизированные комплексы полунатурного моделирования процессов функционирования автономных систем ближней радиолокации. -М.: Гениус Медиа, 2011. -180 с.
- Борзов А.Б., Быстров Р.П., Засовин Э.А., Лихоеденко К.П., Муратов И.В., Павлов Г.Л., Соколов А.В., Сучков В.Б. Миллиметровая радиолокация: методы обнаружения и наведения в условиях естественных и организованных помех. -М.: Радиотехника, 2010. -376 с.
- Уфимцев П.Я. Основы физической теории дифракции. -М.: Бином, 2009. -352 с.
- Борзов А.А., Борзов А.Б., Сучков В.Б. Многоточечная модель радиолокационной цели в задачах синтеза входных сигналов радиовзрывателей./Оборонная техника, 2007. -№ 3-4. -С. 43 -55.


