Метод определения звукоизолирующих свойств локально реагирующих материалов in situ

заЙцев к.и.

Половнев а.л.

Пушкин С.д.

наГиБин н.С.        Сычев а.в.

При проектировании космической техники необходимо знать звукоизолирующие свойства различных материалов для обеспечения требований норм прочности и условий среды обитания космонавтов.

В данной статье рассматривается применение нового метода для определения звукоизолирующих свойств локально реагирующих материалов in situ с помощью нового спаренного датчика (микрофлоуна), позволяющего в одной и той же точке одновременно измерять акустическое давление и скорость частиц, и микрофона, встроенного в жёсткое основание, на котором располагается исследуемый материал.

В испытаниях использовалась штатная сборка микрофлоуна с точечным источником звука на расстоянии 0,26 м от микрофлоуна. Данная сборка при расположении микрофлоуна на расстоянии ~0,005 м от поверхности образца позволяет in situ определять поверхностный импеданс локально реагирующего материала с использованием той или иной процедуры коррекции на сферичность источника для пересчёта на случай плоской волны [1–9]. Для правильного определения поверхностного импеданса образца линейные размеры его поверхности должны быть не менее 0,3 м.

В качестве основания, на котором располагался исследуемый материал, использовался лист вакуумной резины 0,5×0,5 м толщиной 0,01 м, в центре которого было сделано отверстие под микрофон диаметром 0,0063 м (рис. 1). Для обеспечения большей жёсткости к листу резины снизу были приклеены пять стальных полос 0,1×0,5 м толщиной 0,01 м.

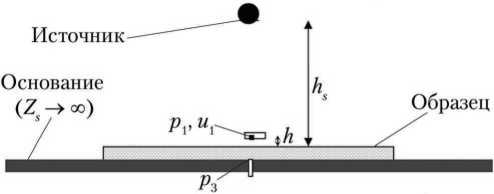
Рис. 1. Схема испытаний образца звукопоглощающего материала: p ₁ , u ₁ — давление и скорость на расстоянии h от поверхности образца (микрофлоун); p ₃ — давление на основании (микрофон); h — расстояние от микрофлоуна до поверхности образца; h_s — расстояние от источника до поверхности образца; Z_s — поверхностный импеданс (рисунок создан авторами)

В случае локально реагирующего материала при нормальном падении плоской звуковой волны на границу материала можно использовать метод переходных матриц для связывания значений давления и скорости на границах образца. Учитывая, что скорость колебаний частиц воздуха на жёстком основании равна нулю, можно записать следующее:

p ₀ u ₀

A B p ₃

C D u ³

A ∙ p

C ∙ p ₃ ³

где p ₀ , u ₀ — давление и скорость на поверхности образца; p ₃ , u ₃ — давление и скорость на основании ( u ₃ = 0); A , B , C , D — искомые коэффициенты переходной матрицы.

Из стандартных измерений микро-флоуном может быть найден поверх- p ₀ ностный импеданс образца Z = ^s u ₀ (или комплексный коэффициент отражения R ), откуда можно определить лишь соотношение .

C

В действительности, чтобы найти коэффициенты A и C по отдельности, необходимо модифицировать стандартную процедуру калибровки микрофлоуна в свободном поле. Рядом с датчиком p1 микрофлоуна или на месте микрофлоуна (в случае калибровки гармоническим сигналом с нарастающей частотой) размещается микрофон p3, что позволяет найти взаимную комплексную передаточную функцию H13    между датчиками p1 и p3:

p

H 13 = _p ³ ₁ .                                   (2)

При этом надо учитывать, что давление p ₁ на датчике микрофлоуна отличается от давления p ₀ на поверхности образца, так как микрофлоун находится на расстоянии h = 0,005 м от поверхности образца.

Для нахождения передаточной функции между p ₀ и p ₁ воспользуемся методом мнимого источника.

В свободном поле зависимость давления   p,   генерируемого точечным источником, от расстояния в комплексном виде выражается следующей формулой:

p ( r ) = i p ck —— e ^ikr ,                      (3)

4л r где r — расстояние от источника; i — мнимая единица; ρc — импеданс среды; k — волновое число; Q — объёмная скорость источника.

С учётом мнимого источника относительно отражающей поверхности давление на поверхности образца можно выразить следующей формулой:

QQ p0 = ipck    , e^khs + Ripck    , e^khs

4Лh             4Лn ss

= (1 + R ) i p ck . . e ^ikh s ,                            (4)

4л h где R — комплексный коэффициент отражения; hs — расстояние от точечного источника до поверхности образца.

Давление p ₁ (микрофлоун) на расстоянии h от поверхности образца запишется следующим образом:

p 1 = i p ck

Q

4л ( h_s - h )

_e –ik ( h_s – h ) ₊

Q

+ Ri p ck ——..----, ,

4л( h_s + h )

_e –ik ( h_s + h )

Из формул (4) и (5) получим передаточную функцию между давлениями p ₁ и p ₀ :

p 0

H _{10     p 1}

(1 + R) h s e–ikhs

e –ik ( h_s – h )          e –ik ( h_s + h )

+ R h_s – h       h_s + h

Коэффициенты A и C переходной матрицы (1) находятся согласно следующим формулам:

H

^A = ( p i ^H 13 ) ~p; ;

C = Z_s / A .

Падение звуковой волны от мнимого источника равносильно перевороту образца. При перевороте образца на преграде переходная матрица обращается, но изменяется и направление скорости, поэтому формула (1) принимает следующий вид:

p 0

^-u 0

к 7

A B

C D

P 3

— u 3

где p ′ ₀ , u ′ ₀ — давление и скорость на поверхности образца; p ′ ₃ , u ′ ₃ — давление и скорость на основании ( u ′ ₃ = 0); ∆ — определитель переходной матрицы.

Аналогично уравнению (1), из уравнения (9) можно определить соотно- шения и -^, откуда однозначно находятся определитель ∆ и параметр D. Параметр B получается автоматически из формулы определителя матрицы:

AD — А

_{B =}        .                          (10)

C

В случае однородного образца параметры переходной матрицы в рамках теории эквивалентной жидкости определяются следующим образом:

A = D = cos(kсd);(11)

sin( k d )

C = j Zс ;(12)

c

B = j sin(kсd)Zc;(13)

∆ = (AD – BC) = 1,(14)

где d — толщина образца; k_с — волновое число эквивалентной жидкости; Z_c — характеристический импеданс эквивалентной жидкости.

Отсюда следует, что для однородного образца достаточно провести одно испытание, чтобы получить все коэффициенты переходной матрицы с учётом выражений (11) и (12):

D = A ;                             (15)

AD – 1

B =        .                          (16)

C

Зная коэффициенты переходной матрицы, звукоизоляцию образца можно определить по следующей формуле:

TL = 10 lg

B

A +   + C p c + D .

P c             J

Для однородного материала можно определить его характеристические свойства, исходя из найденных коэффициентов переходной матрицы:

k_c = _d cos ^–1 ( A );

Z_c = jZ_s tg( k_c d ).

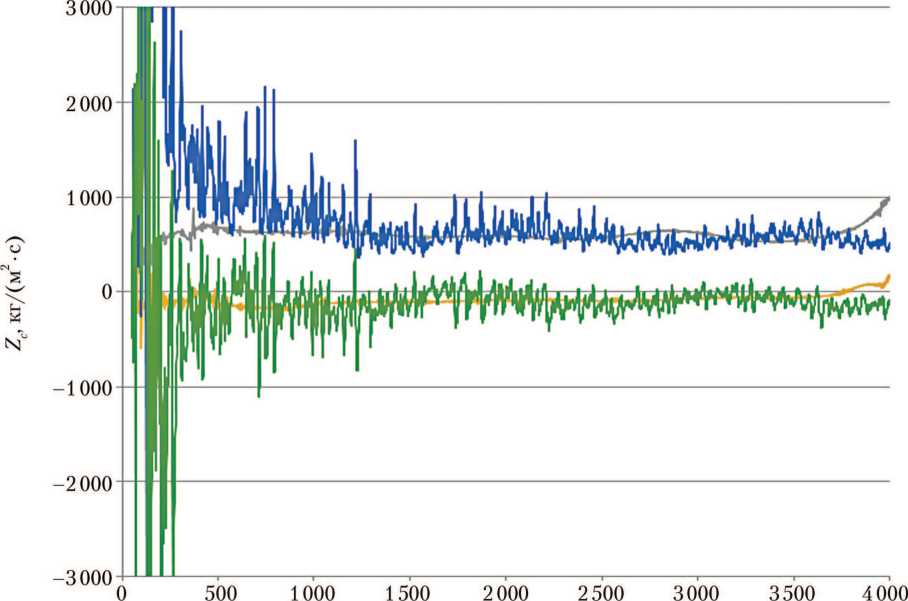
На рис. 2–4 представлены акустические свойства авиационного поролона, полученные предложенным методом, в сравнении с результатами, полученными методом двух нагрузок в импедансной трубе с внутренним диаметром 0,05 м [10].

Как видно на рис. 2–4, микрофлоун совместно с точечным источником звука и микрофоном, встроенным в жёсткое основание, позволяет с приемлемой точностью получать акустические характеристики однородных звукопоглощающих материалов in situ в обычных условиях офисных помещений на частотах свыше 500 Гц.

Ограничение применимости метода на низких частотах связано с точечным источником звука, облучающим образец. Во-первых , фронт звуковой волны вблизи поверхности образца (на расстоянии 0,26 м от источника) можно приближённо рассматривать как плоский (что необходимо для применимости метода переходных матриц) лишь на частотах свыше 300 Гц. Во-вторых , при наличии в помещении с образцом низкочастотного фонового шума эта частота может сдвинуться ещё выше из-за малой эффективности излучения точечного источника на низких частотах.

Если сам образец обладает небольшим коэффициентом звукопоглощения, что характерно для достаточно тонких звукопоглощающих материалов именно в низкочастотной области, то скорость колебаний частиц вблизи поверхности такого образца, лежащего на жёстком основании, стремится к нулю. Это приводит к уходу сигнала датчика скорости микрофлоуна в фоновые шумы, что, в свою очередь, ведёт к увеличению погрешности метода на низких частотах.

В высокочастотной области погрешность метода обусловлена точностью взаимной калибровки микро-флоуна и микрофона, встроенного в жёсткое основание.

Предложенная методика с применением микрофлоуна и микрофона позволяет также определять/оценивать звукоизолирующие свойства покрытий, что достаточно проблематично сделать в импедансных трубах ввиду значительного влияния условий закрепления образца в трубе.

На однородный звукопоглощающий материал (ЗПМ) с известной переходной матрицей A накладываем покрытие и экспериментально находим переходную матрицу B сборки (покрытие + ЗПМ), после чего, используя обратную матрицу образца ЗПМ, получим переходную матрицу покрытия A : c

B = A_cA ⇒ A_c = BA ^–1 .              (20)

На рис. 5 приведено сравнение оценок звукоизоляции материала «Ламкотек» (тонкая нейлоновая ткань с покрытием из полиуретана), полученных с помощью микрофлоуна и дополнительного микрофона, встроенного в основание согласно предложенной методике, и в импедансной трубе.

Как видно из рис. 5, оценка звукоизоляции материала «Ламко-тек», полученная с помощью предложенной методики, значительно ближе к ожидаемому результату, чем данные, полученные с помощью импедансной трубы, за исключением области частот в районе 1 кГц, где наблюдается резонанс в материале (реакция материала перестаёт быть локальной).

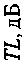
Частота, Гц

Рис. 2. Звукоизоляция TL авиационного поролона (плотность 35 кг/м³, толщина 0,015 м): — — импедансная труба;

— _— микрофлоун (рисунок создан авторами)

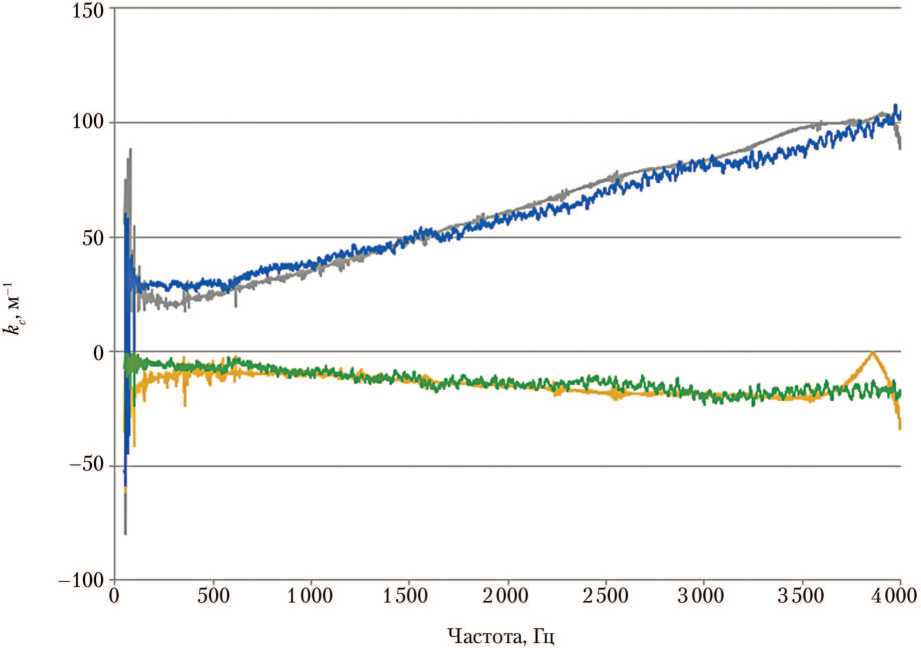
Рис. 3. Реальная и мнимая части волнового числа k_c авиационного поролона (плотность 35 кг/м³, толщина 0,015 м): — — реальная часть (импедансная труба); — — мнимая часть (импедансная труба); — — реальная часть (микрофлоун); — — мнимая часть (микрофлоун) (рисунок создан авторами)

Частота, Гц

Рис. 4. Реальная и мнимая части характеристического импеданса Z_c авиационного поролона (плотность 35 кг/м³, толщина 0,015 м): — — реальная часть (импедансная труба); — — мнимая часть (импедансная труба); — — реальная часть (микрофлоун); — — мнимая часть (микрофлоун) (рисунок создан авторами)

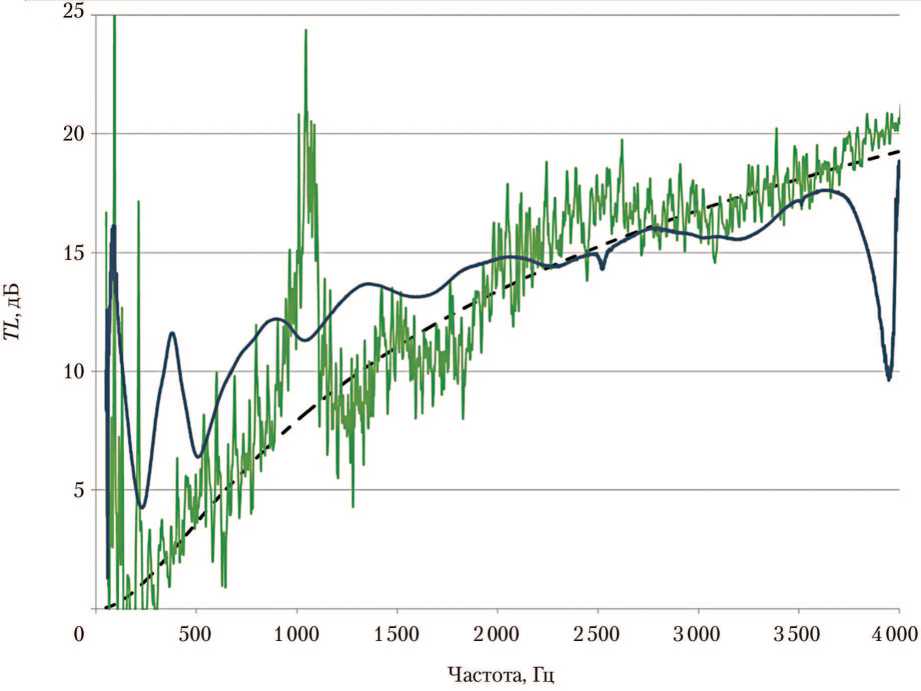
Рис. 5. Оценка звукоизоляции TL материала «Ламкотек» (погонная масса 0,3 кг/м²): — — — — закон массы; ^— — микрофлоун; ^— — импедансная труба (рисунок создан авторами)

Авиационный поролон и «Ламко-тек» применяются в сборке многослойной герметичной трансформируемой оболочки [11], при этом слои поролона могут собираться не только последовательно, но и параллельно, с воздушными зазорами между ними. Предложенный метод позволяет эффективно определять свойства материалов, которые могут быть использованы для расчёта звукоизоляции сложной трёхмерной многослойной конструкции модифицированным методом переходных матриц, позволяющим учитывать влияние параллельной сборки материалов [12].

Выводы

Предложен новый метод определения звукоизоляции локально реагирующих материалов in situ.

В оценке звукоизоляции тонких покрытий предложенный метод оказался предпочтительней измерений в импедансной трубе.

Предложенный метод может быть использован для эффективной оценки характеристик материалов с целью их дальнейшего применения при оценке звукоизоляции многослойных материалов методом переходных матриц параллельной сборки.