Метод оптимального управления экзоскелетом нижних конечностей с упругими элементами

Оригинальное эмпирическое исследование

Original Empirical Research

Optimal Control Method for a Lower Limb Exoskeleton with Elastic Elements

Delshan Deeb © H , Igor V. Merkurye v

National Research University “MPEI”, Moscow, Russian Federation

Introduction. Modern development of exoskeletons opens new horizons for rehabilitation and improving the quality of life of people with limited mobility. The relevance of the study on methods of optimal control of exoskeletons is due to the growing demand in medicine and industry. However, there are numerous challenges related to the efficient control of exoskeletons, especially in the context of the integration of elastic elements. Topics related to optimal control and tuning of system parameters to reach maximum efficiency and user comfort remain insufficiently studied. The objective of this study is to develop a method of optimal control of a lower limb exoskeleton (LLE) with elastic elements while optimizing energy costs and accounting for external disturbances.

Materials and Methods . The LLE is represented by a simplified model of an inverted pendulum with elastic elements in the feet. The dynamic model of the LLE was developed using Lagrange equations. The optimal control method was based on the synthesis of a linear quadratic regulator designed to minimize energy costs. To account for the influence of external disturbances, a Kalman filter was integrated into the control loop. The parameters of the mathematical model of the LLE were obtained from published data. System simulation was performed in the Wolfram Mathematica environment.

Results. A method of optimal control of the LLE with elastic elements has been developed. This method optimizes energy costs while maintaining vertical equilibrium. The system was modeled using optimal terminal control, followed by optimal feedback control. During feedback control, key parameters affecting system stability were identified: spring stiffness and damping coefficients. Integration of the Kalman filter enabled compensation for external disturbances.

Discussion . The use of terminal control within the developed method reduced energy costs by 98% within a specified stabilization timeframe. Optimal values of spring stiffness and damping coefficients for obtaining the best system response were identified. The use of the optimal control method of the LLE in combination with the Kalman filter confirmed the effective compensation of external disturbances and noise, which provided the convergence of transient processes with minimal energy consumption.

Conclusion . The proposed method for achieving optimal control while minimizing energy costs is a promising solution in the field of control signal calculation required to ensure stability and determine the optimal energy cost function. This is especially true for medical rehabilitation tasks. These results may be useful for further research and development in the field of robotics and wearable devices.

Введение. Экзоскелеты нижних конечностей (ЭНК) вызывают всё больший интерес, обусловленный необходимостью решения глобальных проблем здравоохранения — старения населения и роста числа нервно-мышечных травм [1] . Эти устройства призваны обеспечить эффективные решения для поддержки и улучшения двигательных функций человека, например, для помощи при ходьбе [2] , реабилитации и компенсации потери равновесия [3] , тем самым повышая независимость и качество жизни.

Механика

ЭНК часто проектируются без упругих элементов из‑за возросшей сложности процесса стабилизации во время движения и влияния дополнительных факторов, возникающих при использовании упругих элементов [4] . С другой стороны, для этих экзоскелетов могут требоваться упругие элементы, которые улучшают способность конструкции адаптироваться к неровным поверхностям. Упругие элементы могут быть установлены в области голеностопного сустава [5] или использоваться для его полной замены [6] .

Управление ЭНК является сложной задачей. Ранее были предложены различные подходы к её решению. Разработка эффективного метода управления зависит от множества факторов, поддерживая постоянную актуальность исследований в этой области. Для управления ЭНК существуют разные методы: адаптивный метод управления [1, 7] , робастные (устойчивые) методы [8, 9] и метод оптимального управления [10, 11] . Несмотря на эффективность первых двух методов, третий является наиболее удачным. Метод оптимального управления учитывает не только повышение устойчивости и эффективности управления ЭНК в динамических и непредсказуемых условиях, но и позволяет снизить энергозатраты и расход ресурсов системы управления [10, 11] . Однако интеграция упругих элементов в стопы ЭНК приводит к осложнению управления ими. Кроме того, учет внешних возмущений при управлении ЭНК сопровождается новыми проблемами в обеспечении динамической устойчивости системы управления ЭНК.

На основании вышеизложенного можно утверждать, что существует необходимость в разработке метода оптимального управления ЭНК с упругими элементами. Поэтому целью данного исследования явилась разработка метода оптимального управления экзоскелетом нижних конечностей и упругими элементами при оптимизации энергозатрат и учете внешних возмущений. Данный метод позволяет минимизировать квадратичную функцию энергозатрат при наличии упругих элементов и внешних возмущений.

Одним из факторов, еще больше усложняющих решение вопроса динамической устойчивости ЭНК, является наличие белого шума, который представляет собой помеху управляющему сигналу [12] , который был исследован в данной работе.

Для достижения поставленной цели были поставлены следующие задачи:

• -    разработка математической модели перевёрнутого маятника с упругими элементами в стопах;

• -    разработка метода оптимального управления ЭНК с упругими элементами;

• -    учет влияния внешних возмущений (гауссовского белого шума);

• -    проведение численного моделирования в среде Wolfram Mathematica для двух типов управлений: терминальное управление и управление с обратной связью;

• -    анализ полученных результатов исследования переходных процессов основных параметров динамики ЭНК

с упругими элементами.

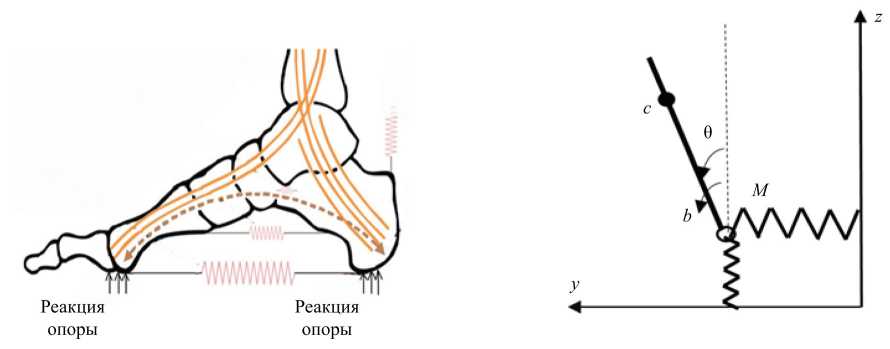
Материалы. С целью разработки математической модели ЭНК с упругими элементами в стопах рассматривается его кинематическая схема. Стопа представлена упругими элементами и соединена с моделью по типу перевернутого маятника (рис. 1). Модель включает инерционные свойства, кинематические ограничения суставов и внешние силы, действующие на систему .

а)                                                                     б)

Рис. 1. Кинематическая схема ЭНК: а — биомеханическая модель физиологической «рессоры стопы» 1 ; б — упрощённая динамическая модель экзоскелета:

с — центр массы; θ — угол голеностопного сустава; М — момент управления

• ¹    Субботин Ф. Биомеханика стопы. Часть 1. Школа Фиделя Субботина; 2024. URL : https://fs-school.ru/blog/988624 ( дата обращения: 10.05.2025).

Характеристики упругих элементов и параметры модели следующие: ky, kz — коэффициенты жёсткости гори- зонтальной и вертикальной пружин, соответственно. Их значения — ky £ [500,1 500] Н/м [13], kz £ [7 000, 20 000] Н/м [14]. cy, cz — коэффициенты горизонтального и вертикального демпфирования, соответственно, cy £ [30, 200 Н^с/м], cz £ [500-2 000 Н^с/м] [15]. Jc =1 m h2 — момент инерции экзоскелета относительно центра масс, кгм2; m = 70 — масса экзоскелета с пациентом, кг; h = 1 — длина экзоскелета до центра масс, м;

μ y = 0,7 и μ z = 0 — коэффициенты трения; N y = 0 и N z = m g — нормальные силы, Н; g = 9,8 — ускорение свободного падения, м/с².

Методы. Динамика ЭНК описывается уравнениями Лагранжа второго рода в общем виде 2 :

d IdL dt [д q i

jL- = Qi,  (i = 1,..., 3), д qt

где L = T – V — функция Лагранжа; T — кинетическая энергия системы; V — потенциальная энергия системы; Q — обобщенные силы; q = (θ, y b , z b ) ^T — вектор обобщенных координат; θ — угол поворота звена экзоскелета, отсчитываемый от горизонтальной поверхности (параллельной опорной плоскости) в направлении против часовой стрелки; y b , z b — горизонтальное и вертикальное перемещение основания.

Координаты центра масс маятника определяются следующими уравнениями:

yc = Уь + hsin 0;(2)

zc = zb + h cos 0.

Кинетическая энергия маятника задается по формуле:

T=2 mv2 + 2 Jc0 2, где v — скорость центр масс, равен y>2 + z2 = (y’b+h cos 9 9) + (zb+h sin 9 9) .

Потенциальная энергия систем описываются следующим уравнением:

V = mgzc + 2 kzZb + 2 ky Уь.

Обобщённые силы демпфирования, применяемые с помощью функции диссипации Рэлея для моделирования линейного демпфирования, записываются в виде [15] :

демп   дD          1

Qi   = ~; D = Tcyyb + Fczzb.

• q,          22

Модель трения Кулона задаётся следующими уравнениями [15] :

Q m = -Ц y N yt anh ( a y ь ) ; Q m^p = -Ц z N z tanh ( a z b ) ,

где α >> 1 — параметр регуляризации (для аппроксимации разрывной функции sign ( v )), в данной работе выбран a = 100.

После промежуточных вычислений, уравнения (2–6) принимают вид:

( mh ² + J_c ) 0 + mhcos ( 0 ) y_b - mhsin ( 0 ) Z_b - mghsin ( 0 ) = M ;

my_b + mhcos ( 0 ) 0- mhsin ( 0 ) 0 ² + k_yy_b = - c_yy_b -ц _yN_y tanh ( a y_b ) + F yx ;                  (7)

mzb - mhsin(0)0-mhcos(0)02 + kzzb = -czZb -цzNz tanh(azb) - mg + Fzxx, где M, Fyext , Fzext — внешние обобщенные силы.

В окрестности вертикального равновесия (θ ≈ 0) справедливы допущения: sin θ ≈ θ, cos θ = 1, z b ≈ – mg / k z . Уравнения (7) линеаризуются с учетом малости (9², 9 ) ^ 0 и tanh (ay _b ) « ay b при малых скоростях:

( mh ² + J_c ) 0 + mhy_b - mgh 0 = M ;

my ь + mh 0 + k y У ь =- c y y_b -ц y N y a y_b + F yx ;                            (8)

mz b + k z z b = - c z z b -Ц z N z a z_b + FF .

При предположениях о малых углах вертикальное перемещение z становится динамически независимым от горизонтального y и углового θ состояний. Его поведение сводится к гармоническому осциллятору, который может анализироваться отдельно [12] .

Механика

Для синтеза управления представим систему в канонической форме пространства состояний с учетом внеш- них возмущений и шумов измерений. Задав вектор состояния [x 1, x2, x3, x4]T=[0, 9, y, y]T, запишем систему в форме Коши:

x ( t ) = Ax ( t ) + Bu ( t ) + Dw ( t ) ; y ( t ) = Cx ( t ) + v ( t ) ,

где A — матрица состояния; B — матрица управления; u ( t ) — вектор управляющих сигналов; D — матрица возмущений; w ( t ) — вектор внешних возмущений; C — матрица измерений; v ( t ) — вектор внешних возмущений.

Основная задача регулятора заключается в переводе динамической системы из начального состояния x ( t 0 ) в заданное конечное состояние x ( t 1 ) за определенное время t 1 .

Грамиан управляемости W характеризует способность системы достигать произвольных состояний за конечное время T и определяется по формуле [12] :

W

f t i

Ф ( 1 0 ,t ) B ( t ) B T ( t ) Ф T ( 1 0 ,t ) dt , t 0

где Ф( t 0 , t ) = e ^{A ( t 0 – t )} — матричная экспонента.

Система является полностью управляемой на [ t 0 , t 1 ] тогда и только тогда, когда W ( t 1 , t 0 ) обратима. Если Грамиан обратим, любое состояние x_T £ R n может быть достигнуто с помощью соответствующего управления u ( t ) [12] .

Управление, которое минимизирует квадратичную функцию энергозатрат и переводит систему из состояния x ( t 0 ) в состояние x ( t 1 ), имеет вид [12] :

u ( t ) = - B T ( t ) Ф T ( 1 1 ,t ) ^W "1 ( 1 1 ,t о ) [ x ( t о ) — Ф ( t о ,t i ) x ( 1 1 ) ] .                               ⁽¹¹⁾

После промежуточных вычислений квадратичную функцию энергозатрат можно рассчитать с помощью выражения (12):

J min =[ x ( t о ) - Ф ( t о ,t 1 ) x ( 1 1 ) ] T W ^-1 ( 1 1 ,t о ) [ x ( t о ) - Ф ( t о ,t 1 ) x ( 1 1 ) ] .                         ⁽¹²⁾

Управление, заданное уравнением (11), является программным (разомкнутым) и зависит от времени. Для обеспечения асимптотической стабилизации системы в начало координат при произвольных начальных условиях необходим синтез закона управления замкнутого контура, основанного на обратной связи по состоянию в реальном времени. Задача управления формулируется в виде минимизации квадратичной функции энергозатрат [12] :

TO

J = J [ x^T ( t ) Qx ( t ) + x^T ( t ) Rx ( t ) ] dt .                                         (13)

где R — положительно определенная матрица; Q — положительно полуопределенная матрица.

Оптимальное управление, обеспечивающее минимизацию энергозатрат, может быть реализовано в виде отрицательной обратной связи с переменными параметрами:

u ( t ) = - k ( t ) x ( t ) ,

где k ( t ) = R ^–1 B ^T P ( t ); k ( t ) — матрица коэффициента обратной связи; P ( t ) — решение уравнения Риккати.

Для нахождения P ( t ) при t → ∞ необходимо решить алгебраическое уравнение Риккати, которое задается следующим образом:

- A T P - PA + PBR ¹ B^TP - Q = 0,                                (15)

Система с управляющим сигналом u ( t ) описывается уравнением:

x ( t ) = Ax ( t ) - BKx ( t ) = [ A - BK ] x ( t ) .                                      (16)

На практике измерение всех состояний невозможно из-за ограниченного числа датчиков, шумов и погрешностей измерений [12] . Для оценки вектора состояния по входам и выходам используется оптимальный фильтр Калмана.

Система с управляющим сигналом u(t) и фильтр Калмана для определения вектора состояния имеет следующий вид [12] :

x ( t ) = Ax ( t ) + Bu ( t ) + L [ y ( t ) - Cx ( t ) ] ,                                      (17)

где x — оценочное состояние; Cx — выход наблюдателя; L — матрица усиления Калмана.

При наличии внешних возмущений w ( t ) и шума измерений v ( t ) с нулевыми математическими ожиданиями M [ v ( t )] = 0, M [ w ( t )] = 0 и ковариационными матрицами s w и s v , соответственно, матрица коэффициента усиления L определяется из решения алгебраического уравнения Риккати (18) и соответственно найдется стационарный фильтр Калмана:

AP x + P x A ^T - P x C T s v¹ CP x + Ds_wD‘ = о; L = P x C T s - ¹.

Управление линейной нестационарной системой при внешних возмущениях на входе и выходе реализуется с помощью линейной обратной связи по оценке состояния:

u (t) = - k (t) x (t).

Вид замкнутой системы с обратной связью по оценке вектора состояния определяется формулой:

d f * 1

dt ˆx

2 n x 1

A - BK BK 1   f x 1    fD w

+

0 A - LC L , [ x L , 1 L y 2 n x 2 n 2 n x 1

После разработки метода оптимального управления ЭНК с упругими элементами и учетом влияния внешних возмущений остается произведение численного моделирования и анализ полученных результатов исследования переходных процессов по углу отклонения и смещению. Для достижения этого на первом этапе метод оптимального управления сфокусировали на восстановлении равновесия за определенное время стабилизации без учёта промежуточной траектории движения. На втором этапе метод оптимального управления с обратной связью был применен для поиска оптимальной промежуточной траектории движения как с применением фильтра Калмана, так и без него.

Результаты исследования. В работе были исследованы переходные процессы управляющего момента, силы, смещения и угла при переходе ЭНК с упругими элементами из неустойчивого положения в положение вертикального равновесия. Результаты численного моделирования приведены на рис. 2–6 при трех начальных условиях: Y 1 = [1/10, 0, 0 ,0], Y 2 = [1/10, 0, 1/10 ,0], Y 3 = [1/10 0 1/10 0 0 1/10 0 1/20 0].

Результаты терминального управления рассчитаны для времени стабилизации 0,6 с. На рис. 2 представлены кривые управляющих моментов разомкнутой системы при начальных условиях Y 1 и целевом положении в состоянии вертикального равновесия. Синяя кривая соответствует управляющему моменту M , оранжевая — управляющей силе F y .

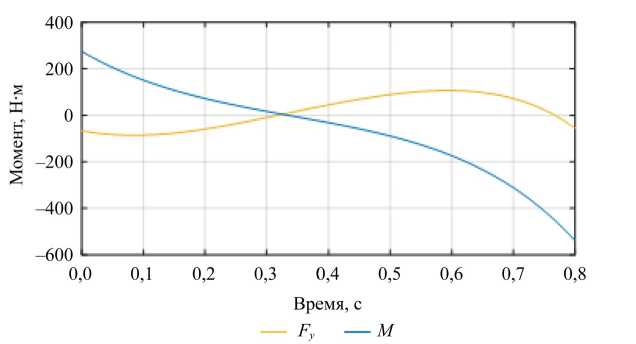
Рис. 2. Кривые управляющих сигналов разомкнутой системы

Значения квадратичной функции энергозатрат при терминальном управлении для различных значений времени стабилизации рассчитаны по уравнению (12) и представлены в таблице 1. Можно заметить снижение значения функции энергозатрат при увеличении времени стабилизации.

Таблица 1

Значения квадратичной функции энергозатрат

Время стабилизации, c	0,1	0,2	0,3	0,4
Значение квадратичной функции энергозатрат (J)	1 648,8	212,1	66,1	29,9

На рис. 3 представлены кривые переходных процессов основных параметров динамической системы ЭНК (θ, y b ) при начальных условиях Y 1 . Синяя кривая представляет собой переходный процесс угла отклонения θ, а оранжевая — изменение координаты по оси ординат y b в течение заданного времени стабилизации 0,6 с при терминальном управлении.

Механика

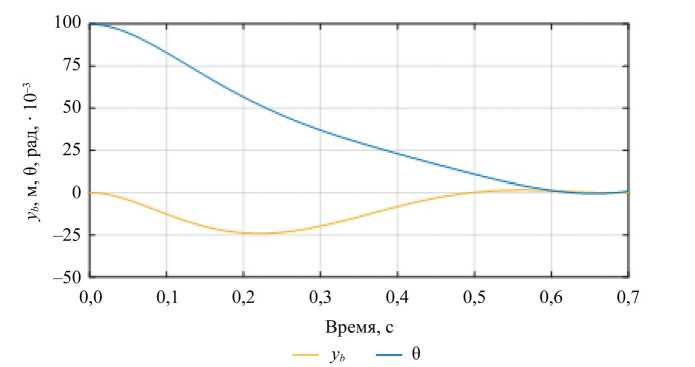
Рис. 3. Кривые переходного процесса

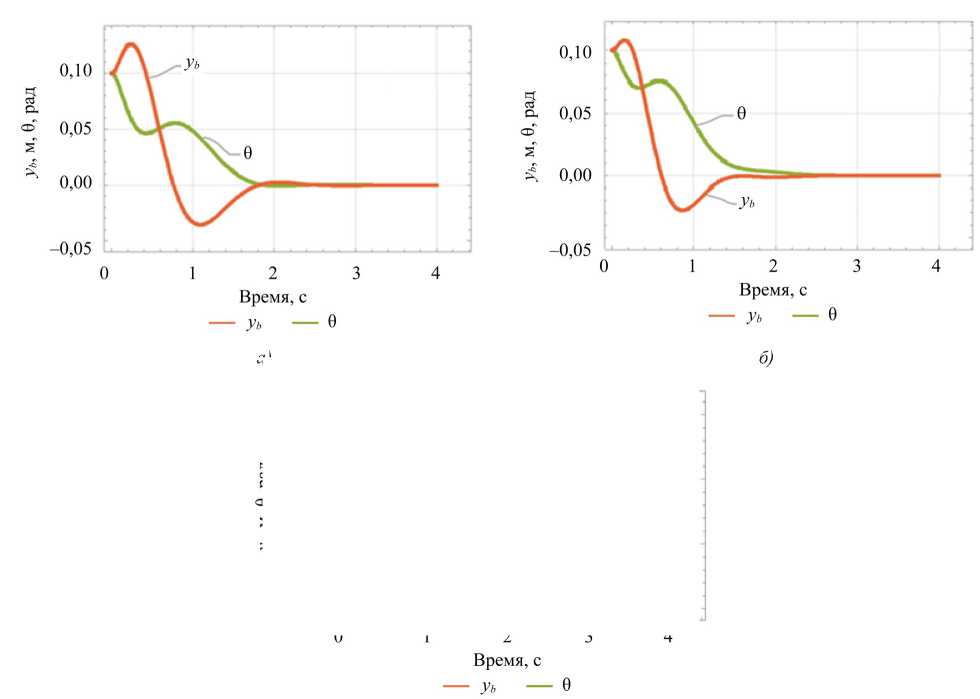
Результаты моделирования на рис. 4–6 получены с применением типа управления с обратной связью, которое позволяет провести поиск оптимальной промежуточной траектории движения. Для исследования влияния жесткости упругих элементов (изменения коэффициента жесткости пружины k y ) на устойчивость динамической системы ЭНК при минимизации энергозатрат были рассмотрены переходные процессы основных параметров динамической системы ЭНК (рис. 4) при начальных условиях Y 2 и следующих параметрах системы с обратной связью: c y = 100, k z = 20 000, Q = eye (4) ⋅ 10 ³ , R = eye (2).

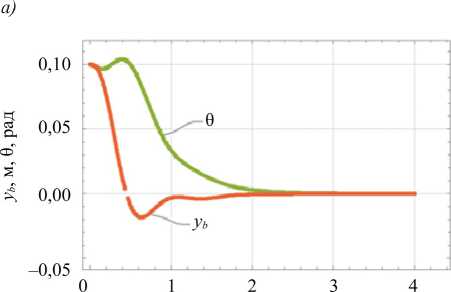
Оранжевая линия представляет собой зависимость y b , а зеленая линия — θ. Значения коэффициента жесткости были выбраны следующие: k y = [700, 1 000, 1 500] Н/м. Переходные процессы представлены соответственно на рис. 4 a , б, в .

в)

Рис. 4. Переходные процессы при изменении коэффициента жесткости пружины: а — при k y = 700 и c y = 100; б — при k y = 1 000 и c y = 100; в — при k y =1 500 и c y = 100

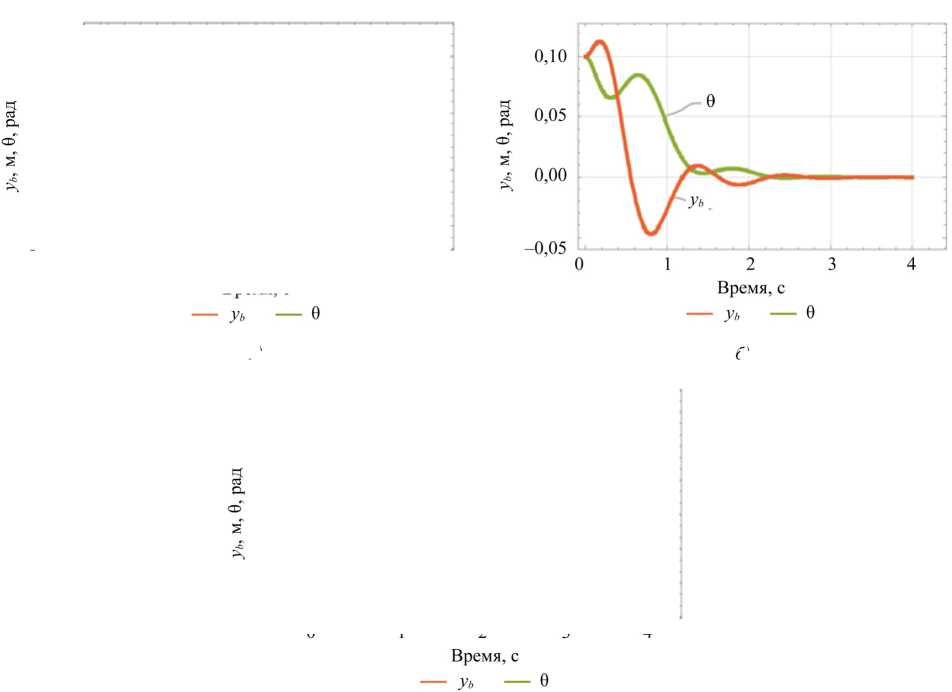
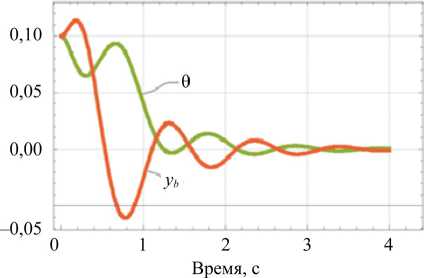
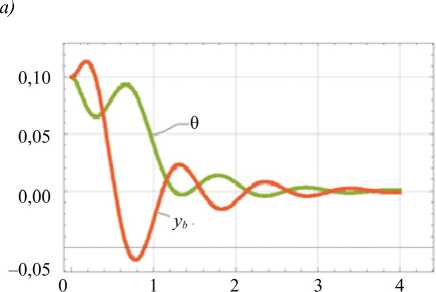
Для исследования влияния демпфирования упругих элементов (изменения коэффициента демпфирования c y ) на устойчивость динамической системы ЭНК при минимизации энергозатрат были рассмотрены переходные процессы основных параметров динамической системы ЭНК (θ, y b ) (рис. 5) при начальных условиях Y 2 и k y =1 000 с обратной связью . Оранжевая линия представляет собой зависимость y b , а зеленая линия — θ. Значения коэффициента демпфирования составляют c y = [0, 50, 100] Н∙с/м, а переходные процессы изображены соответственно на рис. 5 a , б и в .

б)

в)

Рис. 5. Переходные процессы изменении коэффициента демпфирования: а — при c y = 0 и k y =1 000; б — при c y = 0 и k y =1 000; в — при c y = 100 и k y =1 000

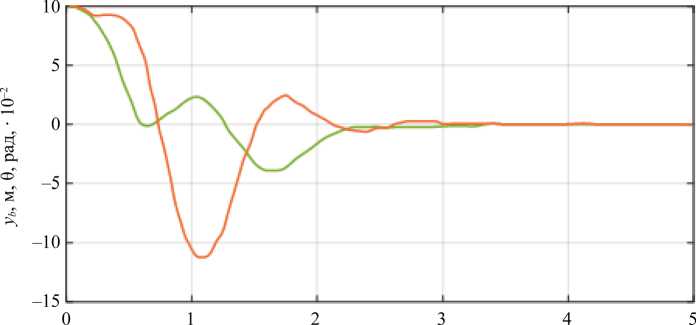
Это исследование также учитывает влияние шума путем добавления фильтра Калмана. На рис. 6 показаны кривые переходного процесса при начальных условиях Y 3 = [1/10 0 1/10 0 0 1/10 0 1/20 0] и ковариационные матрицы s w = eye (1) и s v = 0,1 eye (2). Оранжевая линия иллюстрирует переходный процесс y b , а зеленая линия — переходный процесс θ.

Время, с — у,,   — е

Механика

Рис. 6. Кривые переходного процесса с использованием фильтра Калмана

Обсуждение. Для достижения цели исследования в предыдущем разделе были представлены результаты моделирования, полученные с использованием предложенного метода оптимального управления для минимизации энергозатрат при переходе исследуемого ЭНК из неустойчивого положения в вертикальное положение равновесия.

Из таблицы 1 видно, что по мере увеличения времени, необходимого для достижения целевого устойчивого состояния, энергозатраты пропорционально уменьшаются. Данная зависимость согласуется с динамикой управляющих сигналов: с увеличением допустимого времени стабилизации амплитуды управляющих моментов M и F y уменьшаются, что, согласно формулам (12)–(14), снижает значения энергозатрат. При этом можно сделать вывод о том, что увеличение времени стабилизации (в пределах 0,1–0,4 секунды) снижает энергозатраты на 98 %.

Кривые на рис. 3 демонстрируют переходный процесс длительностью 0,6 с до достижения положения вертикального равновесия, что согласуется с принципами терминального управления (достижение целевого устойчивого состояния за определенное время стабилизации).

Кривые на рис. 4 иллюстрируют влияние изменения коэффициента жесткости на переходные процессы основных параметров динамической системы ЭНК (θ, y b ). Изменение координаты по оси ординат y b при низком значении коэффициента жесткости характеризуется значительным перерегулированием и медленной стабилизацией, а рост коэффициента жесткости исключает перерегулирование и ускоряет стабилизацию системы. Напротив, изменения угла θ демонстрирует обратную зависимость: при низком значении коэффициента жесткости наблюдается плавный переходный процесс без перерегулирования и короткое время стабилизации системы, в то время как увеличение значения коэффициента жесткости до 1 500 вызывает перерегулирование по углу, несмотря на ускоренную стабилизацию. Это противоречие подчеркивает конкурирующую динамику между y b и θ. При коэффициенте жесткости k y =1 000 (рис. 4 б ) достигается оптимальный компромисс: минимизация перерегулирования по координате y b , сохранение стабильности угла θ и быстрая сходимость. Данный режим обеспечивает сбалансированную работу системы.

Достоверность полученных результатов обеспечивается устойчивостью замкнутой системы, что подтверждается отрицательными действительными частями её полюсов для всех исследуемых значений коэффициента жесткости, приведённых в таблице 2.

Таблица 2

Полюса замкнутой системы

Вариант процесса	K y	Полюса замкнутой системы
1	700	–2,2445 + 3,8530i –2,2445 – 3,8530i –4,5071 – 3,2807i
2	1 000	–2,6133 + 5,4608i –2,6133 – 5,4608i –3,6385 – 3,1496i
3	1 500	–2,7679 + 7,5731i –2,7679 – 7,5731i –3,2042 – 3,0242i

Кривые на рис. 5 показывают влияние коэффициента демпфирования . При низком значении коэффициента демпфирования наблюдается значительная вибрация системы перед выходом на установившийся режим, сопровождаемая перерегулированием. Увеличение c y снижает амплитуду колебаний и устраняет перерегулирование, однако приводит к росту энергозатрат. С целью обеспечения баланса между устойчивостью и значением квадратичной функции энергозатрат было выбрано значение коэффициента c y = 100, что гарантирует устойчивость системы управления ЭНК с упругими элементами.

Из изображения на рис. 6 следует, что фильтр Калмана обеспечивает сходимость переходных процессов к нулевым значениям за три секунды при воздействии белого шума, подтверждая его робастные стабилизирующие свойства.

Полученные результаты показывают следующую картину. Во-первых, применение открытого управления как базового этапа позволяет минимизировать энергозатраты на стадии вывода системы из неустойчивого состояния в целевое вертикальное равновесие в заданное время стабилизации. Во-вторых, переход к замкнутому контурному управлению на основе обратной связи по состоянию обеспечивает асимптотическую устойчивость и устойчивость переходных режимов за счет решения уравнения Риккати и реализации эффективного фильтра Калмана. В-третьих, численное моделирование выявило важное влияние параметров упругих элементов на динамику системы: увеличение жесткости пружин уменьшает перерегулирование по углу θ и ускоряет стабилизацию, но может приводить к сложностям на пути к устойчивой траектории; увеличение демпфирования снижает колебания и уменьшает перерегулирование, однако повышает энергозатраты. Найден баланс между стабильностью и энергозатратами, который достигается при конкретных значениях k y и c y (в примерах k y = 1 000 Н/м, c y = 100 Н·с/м).

Исходя из предыдущего обсуждения и анализа полученных в статье результатов можно сказать, что разработанному методу оптимального управления ЭНК с упругими элементами удалось обеспечить устойчивость системы управления данного экзоскелета за определенное время стабилизации и при минимальных энергозатратах.

Заключение. Сформулирована и реализована методика оптимального управления экзоскелетом нижних конечностей (ЭНК) с упругими элементами в стопах с учетом внешних возмущений и шума измерений. Основной подход основан на представлении динамики ЭНК в виде системы уравнений Лагранжа, переводе её в каноническую форму пространства состояний и синтезе управляющего закона через оптимизацию квадратичных функций энергозатрат и устойчивость системы. Для оценки состояния применялся фильтр Калмана, что позволило корректно работать в условиях ограниченного числа датчиков и присутствия внешних возмущений.

Практическая значимость результатов состоит в разработке методики, позволяющей адаптивно выбирать параметры упругих элементов и режим управления в зависимости от условий задачи и целей (минимизация энергозатрат, ускорение стабилизации, минимизация перерегулирования). В рамках потенциальных приложений это может способствовать повышению эффективности реабилитационных технологий, снижению энергопотребления в протезно-ортезных системах и улучшению устойчивости движений на неровных поверхностях. Перспективы исследования включают экспериментальную верификацию метода и его адаптацию к переменным нагрузкам и сложным поверхностям, что особенно актуально для медицинской реабилитации и робототехники.