Метод оптимизации таблиц маршрутизации

Использование бесклассовой междоменной маршрутизации (CIDR) отчасти позволяет решить проблему постоянного увеличения размеров таблиц маршрутизации в Internet-роутерах. Тем не менее, количество записей в реальных таблицах маршрутизации может достигать нескольких десятков тысяч, в связи с этим, актуальным вопросом остается разработка эффективных схем хранения и управления таблицами маршрутизации.

Базовым методом Internet-маршрутизации является сопоставление по наиболее длинному префиксу. Каждая запись таблицы маршрутизации содержит префикс (который может соответствовать не только конкретному узлу, а целой сети) узла назначения и соответствующий ему узел, на который необходимо отправлять трафик. Одному адресу назначения может соответствовать несколько записей в таблице – выбирается же из них та, которая имеет наиболее длинную маску подсети. Рассмотрим фрагмент таблицы маршрутизации (см. таблицу 1). Пусть адрес назначения равен 1 92.168.20.18. В этом случае, в соответствии с алгоритмом поиска наиболее длинного префикса, трафик будет отправлен на узел 1, так как адрес сети, соответствующий первой записи дает большее совпадение разрядов.

Таблица 1. Фрагмент таблицы маршрутизации

Префикс	Узел
192.168.20.16/27	1
192.168.0.0/16	2

Исследователями было предложено несколько программных и аппаратных схем для увеличения скорости поиска в таблицах маршрутизации. Алгоритмические методы включают в себя:локальный поиск,двоичный поиск, использование специальных структур данных (бинарные деревья, трие), хеширование и ряд других. Основным недостатком данных подходов является то, что они требуют нескольких обращений к памяти. Требования к производительности современных сетей являются очень высокими, в то время как время отклика современных архитектур памяти ограничивают возможное количество обращений к памяти.

Одним из наиболее распространенных и перспективных аппаратных решений является контентно-адресуемая память (C AM) [6]. Главной особенностью CAM является то, что адресация осуществляется на основе содержания данных, поиск нужной записи, при этом, может быть осуществлен за одно обращение к памяти. В каждой позиции CAM может быть только 0 или 1. CAM поддерживают только сравнения образцов с фиксированной длиной и, следовательно, в явном виде не подходят для поиска префиксов. Возможным решением является использование нескольких CAM, каждая из которых хранит префиксы определенной длины [3].

Более эффективный подход основан на применении так называемых тернарных CAM. Помимо индекса, TCAM хранят также отдельную маску для каждой записи. Маска определяет, какие из битов индекса являются активными (см. таблицу 2).

Таблица 2. Таблица префиксов, хранящаяся в TCAM

Запись	Префикс	Маска	Следующий узел
1	10100000	11110000	1
2	10110000	11110000	1
3	11011000	11111000	2
4	10001000	11111000	3
5	10111000	11111000	2

Оптимизация таблиц маршрутизации на основе методов построения минимальной ДНФ булевой функции была впервые предложена в [4]. Однако сам алгоритм минимизации, использовавшийся в ней, требует слишком больших вычислительных ресурсов для решения задач большой размерности. В данной работе исследуется метод, дающий такое же качество решения, расходуя на это значительно меньше времени. Рассматриваемая схема оптимизации может быть применена не только к статическим данным – она может быть легко адаптирована для учета изменений, происходящих в таблице маршрутизации [4].

Метод оптимизации таблиц маршрутизации

Введем ряд определений, которые будут использоваться в работе. Пусть задан алфавит {х1 ... xn}. Выражение K = x"1 &... & x=- (iv ф i^ при v ^, 7i e {0,1}, x0 = x , x1 = x )' называется элементарной конъюнкцией. Под булевой функцией будем понимать функцию f (x1;

Под проблемой минимизации булевых функций понимается задача построения для произвольной булевой функции ее минимальной, относительно заданного критерия, ДНФ.

Метод уменьшения размера таблицы маршрутизации, рассматриваемый в данной работе основан на замене нескольких записей на одну. Так, например, записи 1 и 2 из таблицы 2 отличаются только четвертым битом и могут быть скомбинированы (1 0100000, 11100000). Такой подход естественным образом сводится к задаче минимизации ДНФ – префиксам из таблицы маршрутизации мы сопоставляем элементарные конъюнкции, а каждому множеству записей, имеющих одинаковые длины префиксов k и следующий узел u, ставится в соответствие отдельная булева функция. Так, например, записям из таблицы 2, имеющим следующий узел 1, будет соответствовать функция f 4,1 = x 1 X 2 x 1 X₂ v x 1 x ₂ x 1 x ₂ . Операции же объединения записей осуществляются посредством запуска процедуры минимизации ДНФ (относительно количества конъюнкций) для каждой функции f _k,u . Такое преобразование, очевидно, не влияет на процесс маршрутизации, то есть выбор узла, на который необходимо отправлять трафик.

Алгоритм минимизации ДНФ

В работе [4] для уменьшения таблиц маршрутизации использовался минимизатор Espresso-Exact [7]. Повышение быстродействия по сравнению с ним достигается за счет применения более эффективных структур данных – двоичных диаграмм решения, а также модифицированного алгоритма построения минимального покрытия, основанного на методе локального поиска.

Предлагаемый алгоритм минимизации использует для представления булевых функций упорядоченные двоичные диаграммы решения (OBDD) [5], а для покрытий – двоичные диаграммы с отбрасыванием незначащих нулей (ZDD) [5].

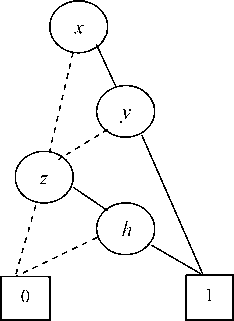
Рис. 1. OBDD–представление для функции f = xy v xzh

Двоичные диаграммы решения (BDD) сочетают в себе два полезных качества – приемлемый расход памяти и, как правило, быстрое выполнение операций над реализуемыми функциями. Упорядоченная двоичная диаграмма решений (OBDD) для заданных функции f ( x 1 ... x n ) и отношения порядка п : V ^ {0; 1 ... n} , где V = { x 1 ... x n } - это направленный ацикличный граф, состоящий из нетерминальных вершин, отмеченных переменными из V и терминальными вершинами, отмеченными булевыми константами 1 и 0. Каждая нетерминальная вершина имеет два исходящих ребра – 1-ребро и 0-ребро. Начальный узел OBDD называется корнем. Для вычисления значения функции на заданном наборе значений переменных мы формируем путь от корня к терминальной вершине следующим образом: если переменная соответствующая текущей вершине принимает значение 1, то выбирается 1-ребро, в противном случае – 0-ребро. В сформированном пути мы можем встретить каждую переменную не более одного раза. На пути от корня к терминальной вершине, переменные встречаются в соответствии с заданным отношением порядка π .

Двоичные диаграммы решения реализуют разделяемое представление для дискретных объектов, размер которого не зависит линейно от их количества. Пример OBDD-представления приведен на рис. 1, где 0-ребра изображены заштрихованной линией, а 1-ребра – обычной.

Для уменьшения размера OBDD применяют следующие правила:

• 1.    совмещение изоморфных подграфов;

• 2.    удаление узлов, оба исходящих узла которых указывают на один и тот же узел.

В случае двоичных диаграмм с отбрасыванием незначащих нулей (ZDD), первое пра- вило сохраняется, а вместо удаления вершин, исходящие ветви которых указывают на один узел, удаляются узлы с единичным выходом, указывающим на 0. Данная разновидность диаграмм решения более эффективна, по сравнению с OBDD, для представления разреженных множеств, в частности, покрытий булевых функций.

Рассматриваемый алгоритм минимизации ДНФ использует классическую схему работы, состоящую из двух этапов:

• -    генерация всех простых импликант функции;

• -    поиск минимального покрытия множества точек, в которых функция принимает значение 1, множеством простых импликант.

Генерация простых импликант, а также удаление доминируемых строк и столбцов осуществляются с помощью методов,предложен-ных в [1].

ДалеезадачупостроенияминимальнойДНФ удобно рассматривать как задачу на покрытие. Пусть M обозначает множество всех точек { m 1 , m 2 ,..., m l } , на которых заданная функция f принимает значение 1, а P = { p 1 , р ₂ ,..., p k } – множество всех простых импликант f . Матрицей покрытия будем называть бинарную матрицу A размерности l х к такую, что A ij = 1 (при этом будем говорить, что j -й столбец покрывает i-ю строку), 1 ≤ i ≤ l 1 ≤ j ≤ k если m _i ⊆ p j , в противном случае A_ij = 0. Требуется найти минимальное количество столбцов, покрывающих все строки матрицы A.

Алгоритм начинается с выбора некоторого допустимого решения s и далее поиск оптимального решения ведется не во всем пространстве поиска, а только в некоторой окрестности s . При этом, если стоимость найденного решения s ′ меньше,чем у s ,то мы устанавливаем в качестве текущего решения s ′ и запускаем поиск по его окрестности.

Начальное решение строится с помощью вероятностного «жадного» алгоритма, который последовательно выбирает простые имп-ликанты в соответствии с (1) [2] до тех пор, пока не будет сформировано полное покрытие.

p = arg max У--------------------- . ⁽¹⁾

£ ^|{ p G P | m G p , m G M ^}|

В случае равенства оценок выбор производится псевдослучайно.

Под окрестностью решения s будем рассматривать множество решений, которые можно получить из s путем удаления, либо добавления 1 элемента. Для ускорения процесса поиска, исследуется не вся окрестность: после удаления элемента решения, выбранного псевдослучайно, запускается «жадный» алгоритм построения минимального покрытия. Таким образом, мы получаем новое допустимое решение. Алгоритм прекращает работу, если на текущей итерации не произошло улучшения текущего решения.

Экспериментальные результаты

Программная реализация рассмотренного алгоритма была выполнена на языке С++, проект был скомпилирован с помощью gcc 3.2. При разработке использовались пакеты CUDD [10] и extra [8].

На рис. 2 показаны результаты сравнения времени работы предлагаемого метода MINDNF и метода Espresso-Exact, использовавшегося для оптимизации таблиц маршрутизации в [4]. В качестве тестовых данных были использованы таблицы, полученные из нескольких крупных точек обмена интернет-трафиком – PAIX и Mae-W est [9]. При этом суммарное время минимизации при использовании MINDNF меньше в 8,25 раз для задач с количеством префиксов к <  10000, и в 22,5 для задач с к >  10000. Метод Espresso-Exact позволяет уменьшить количество записей в таблицах маршрутизации в два раза. Отличие в качестве сжатия для обоих методов незначительно, и составляет порядка 0,001.

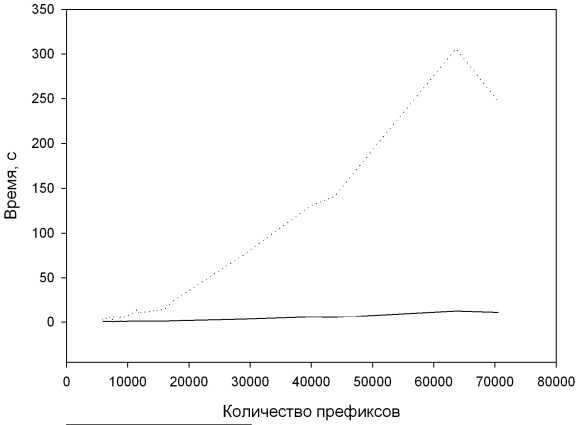
--- MINDNF

........ ESPRESSO-EXACT

Рис. 2. Зависимость времени минимизации от количества префиксов

Заключение

В данной работе рассмотрен метод уменьшения размера таблиц маршрутизации с помощью применения алгоритма минимизации булевых функций. Экспериментальные результаты показывают, что время работы предлагаемого способа минимизации значительно меньше,чем у алгоритмов,приводи-мых в литературе [4]. Качество получаемых решений, при этом, практически не отличается от точных решений.Данный метод может быть использован для оптимизации таблиц маршрутизации большой размерности, реализованных на основе тернарной контентно-адресуемой памяти.