Метод освобождения динамической расчетной модели летательного аппарата

Расчетные динамические модели разрабатываются на этапе проектирования летательного аппарата (ЛА). Они используются в оценках

эксплуатационной нагруженности, обеспечении прочности, управляемости и аэроупругой устойчивости ЛА. По завершению расчетного этапа изготавливается динамически подобная модель (ДПМ) ЛА и проблема аэроупругой устойчивости решается экспериментально [1, 2]. Затем сроится опытное изделие, а за ним и серийные. Расчетные динамические модели сопровождают экспериментальные исследования, опытную и серийную эксплуатацию ЛА. При этом расчетные модели корректируются по результатам наземных модальных испытаний, которым подвергаются ДПМ, опытные и выборочно серийные ЛА [1 – 10].

Важно отметить, что расчетной моделью ЛА является модель свободной динамической системы. В то же время для модальных испытаний авиационная техника либо устанавливается на шасси, либо помещается на специальную систему упругого вывешивания, а космические конструкции - на систему обезвешивания. Системы упругого вывешивания и обезвешивания, влияние которых на свободную конструкцию строго регламентировано [11], являются сложными и дорогостоящими техническими сооружениями. Кроме того, известные методы коррекции математических моделей конструкций не предполагают использование моделей для граничных условий, отличных от тех, что были реализованы в эксперименте [12 - 19]. В настоящей работе предлагается метод освобождения динамической расчетной модели ЛА после проведения процедуры ее коррекции.

МЕТОД ОСВОБОЖДЕНИЯ РАСЧЕТНОЙ МОДЕЛИ

Пусть имеется скорректированная по результатам испытаний закрепленная конечноэлементная (КЭ) модель L некоторой упругомассовой конструкции. Модель описывается матрицами жесткости K и масс M , имеет n степеней свободы и N узлов. Система уравнений собственных колебаний этой модели имеет следующий вид:

KX + MX = 0 . (1)

Ставится задача освободить КЭ-модель от закреплений при условии, что известны инерционные характеристики свободной конструкции, а именно: масса и массовые моменты инерции относительно некоторой точки, например, центра тяжести. Информации об убранных при начальном закреплении модели степенях свободы либо нет, либо она неактуальна, то есть она не позволяет сделать модель свободной. Последнее имеет место быть, например, когда проводится прямая коррекция матрицы жесткости и/или масс закрепленной модели по результатам эксперимента.

Пусть рассматриваемая модель L находится на виртуальной платформе, к которой она прикреплена всеми узлами, которые были зафиксированы. Эта платформа может перемещаться и поворачиваться как жесткое целое. Положение платформы в глобальной неподвижной системе координат будем определять координатами точки C - вектором R 0 = ( x ₀ , y ₀ , z ₀ ) , а ориентация в пространстве задается вектором конечного поворота Q = ( ® , ® 2 , ® ₃ ) [20]. Виртуальная платформа в общем случае находится на упругом основании, заданном тремя линейными и тремя крутильными жесткостями.

При ускорении платформы на закрепленную модель действуют дополнительные силы инерции, обусловленные ускорением каждой точки за счёт перемещения и поворота платформы, поэтому уравнение движения (1) перепишется в следующем виде:

X + X 0 ) = 0 .           (2)

	—* R ,		x 0	( x 0 , y 0 ,.	., ® 3 )
где X 0 = -	... — R n	f = -	... x 0	( x 0 , y 0 ,-	., ® 3 )	■ , i*i = i* 0 + —

x ₀ , y ₀ , z ₀ - линейные перемещения платформы, ®_х 2® 2 , ® 3 - компоненты вектора конечного поворота Q . В случае малых поворотов матрица X линейна относительно компонент этого вектора и имеет следующий вид:

X ( ® , ® ₂, ® ₃ ) =

^ 1 ® ₃ — ® ₂ '

— ® ₃ 1 ® 1

_v ® ₂ — ® 1 _v

Каждый узел КЭ-модели L до деформирования имеет координаты x ⁰ , y ⁰ , z ” , i = 1.. N в своей системе координат, которая необязательно совпадает с системой координат, выбранной выше, тогда точка C в этой системе имеет координаты x ₀ , У ₀ , z о . Так как рассматриваются малые перемещения, то зависимость — = — ( ® ,, ® ₂, ® ₃ ) - линейная относительно компонент вектора конечного поворота [20]:

— = Xr ⁰

1 ® ₃

—®₃ 1

' 1 ® ₃ — ® ₂)

— ® ₃ 1 ® ₁ I

I ® 2 -® 1 ¹ J

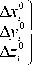
A x⁰ — A z ⁰ ® ₂ + A y ⁰ ® ₃ - A z⁰ ® + A y ⁰ — A x° ® ₃

—A y ⁰ ® ₁ + A x ⁰ ® ₂ + A z ⁰

— ® 2 ^ ® 1 I-

1 л

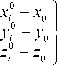
, i = 1.. N .

Для определенности пусть каждый узел описывается тремя линейными и тремя угловыми степенями свободы (хотя в общем случае это может быть не так), тогда выражение (2) с учетом (3) перепишется в следующем виде:

^x 1 x 2

x ₃

x 4 x 5

K - ^x 6

K -

+ M

...

...

...

...

...

xn

x ₄

Х 5 x 6

...

...

...

...

...

■ • x_n

• • • A 0 ^{1 1} A 0 ¹¹ x ₀ — A z ₁ ® ₂ + A y ® ₃ y ₀ + A z 0 ® — A x 0 ®₃ z ₀ — A y₁° ® ₁ + A x 0)2

• ■    •

® ₁

• ■    •

• ■    •

...

z 0 ^{— A} y N ® 1 ^{+ A x} N ® 2

■ •

Раскрывая скобки в (4), получим:

x ₁ x ₂

x ₃ x ₄

x ₅ ^x

u m -

...

...

...

...

...

x n

• ■    ■

x1 ■ ■ x 2

xз x4

• ■    ■

x 5

• ■    ■

^x 6

...

...

...

...

...

• ■    ■

xn J

u m -

[ 1 0 0 ⁰ 0

, 0

0 0

...

.

= 0 (4)

■ x ₀ + m -

' 0 2

J 0

| 0

... 0

.

f y 0 + M -

0 2

J 0

- 0

0 1

...

■ ■ z0

+ M <

0		A z 0		'-A y 0
-Az 0		0		A x 0
A У 0		-A x 0		0
1		0		0
0		1		0
0	■ № i + M .	0	(i)7 + M-	1
0		A z 0	2	-A y 0
-Az 0		0		A x 0
A У 0		-A x 0		0
1		0		0
... 0		... [0		... [0

> (£> ₃ = 0 .

ее

ˆ

Перепишем уравнение (5) в матричном виде:

ˆ

KX + MX = 0,

где X = { X i ,x 2

.

.

.,

x_n x ₀ y ₀

.

.

.

®3 }r, K - матрица жесткости K, дополненная шестью нулевыми столб-

цами, чтобы соответствовать X , а матрицу M можно определить следующим образом:

ˆ

M =

N

^m 11^.

.. m _{1 n}

Z m i, G ji

N

Z m i, G_K2

N

Z m i, G j ,3

N

m 1 G j

+

N

N

j = i

N

^m 21^.

-m 2 n Z m 2, G„ Z m 2, j Z

j = i

m 2, G j ,3

.

..

.

..

..

.

.

.

.

.

.

.

.

.

.

N

N

N

m n 1^.

-m nn Z m nG j , Z m j Z

j = i

^m n , G j ,3

V

^, Z ^+A yj^Om i. G j ,3

j = i

N

N

m

1 G_{j 5}

+

А

-A z ⁰ m. _r j 1, G_{j ,}

^m 2 G j

+

^, Z ^+A y ° m 2 G j ,3

j = i

N

s

-Az0m. r j 2,Gj

.

..

^m n G j

+

,

Z ^+A y >^_ь.

j = i

-Az0 m r j n,Gj

s

,

Z +A z 0 m i, G ji

j = i

N

N

m 1, G_{j ,6}

+

-Ax0 m. r j 1,Gj,3

m 2, G j

+

^, Z ^{+A z 0} m 2, G ji

j = i

N

s

V

-Ax0m. r j 2,Gj,3

.

..

^m n , G ,5

+

^, Z ^+A z ^{0 m} n , G j ,i

j = i

V

^{-A x 0} m n , G j ,3

^, Z ^{+A x 0 m} i, G j ,2

j = i

N

^-A yj°^m i. G ji

m 2, G j ,6

+

^, Z ^{+A x 0} m 2,G j2

j = i

А

s

s

N

V

^-A y ° m 2,G ji

.

..

^m n , G ,6

+

А

,

^, Z ^{+A x 0} m n , G_b2

j = i

V

y j n , G_{j ,1}

s

где матрица (таблица) Gj i – содержит порядковый номер уравнения, соответствующего i-ой степе-

ни свободы j -го узла.

Составим уравнения движения платформы. Пусть c1,2,3

, ^K i,2,3

– линейные и угловые жесткости

крепления платформы. Если платформа свободна, эти жесткости равны нулю. Пусть m0 – общая масса

платформы и конечно-элементной модели L (масса свободной конструкции), а J1 2 3

щие массовые моменты инерции. Тогда можно записать 6 уравнений движения платформы:

– соответствую-

ее

к-% + Ц-^ + S m • X = 0 ,

где

S m =

x ₀

y ₀

^ = <

z

№

№ 2

V® 3

,

< c_i 0 0 0

0 c ₂ 00

о А

к =

Z ^m_G])i

N

m

+

00 c ₃ 0

m ₀ 00

о А

0 0 0 k _i 0

0 0 0 0 к

0 0 0 0 0 к 3

N

,

A =

j 1

2 ²

0 m ₀ 0

.

.

.

.

.

.

m

0 J ₁

,

00 J

000 J ₃

Z m

j 1

n

N

Z m

^G j ,2 ^{, n}

j = i

.

.

.

Z ^mG j3

n

J 1

Z ⁺ m

^A y 0

- m.

m

Z ⁺ m

- m,

A x

m

+

Z ⁺ m

,i A x j ⁰

- m.

, i A у

^mG j 4 2

J 1

Z ⁺ m

j 3

+

, 2 ^A У 0

- m_r

^G j ,2 ^,2

m

j 5

Z + m

А

.

.

.

V 7.

- m_r

Gj

m

, 2 ^A xi

,6 ^,2

+

Z ⁺ mG,

- m,

, A x

'j

, 2 ^A У,

m

G j 4 n

J 1

Z ^{+ m}<

.

.

.

.

.

N

+

^G j 3 ⁿ

^A y j

- m_r „

^G j ,2 ^{, n}

m

Z ⁺ m

j = i

N

n

n

- m.

n

A x¹

.

m

G j 6 n

+

А

+ m_c „

L^      ^Gj o- ⁿ

.

j = i

- m.

A x¹

n

A У 0

Уравнения (6) и (7) образуют новую систему уравнений движения с симметричными матрицами размером ( n +6):

KX + MX = 0,

I K - ( S k ) T ( 0 к

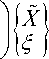
I m 0    1J X

⁺ (s m ( ц - SS m ) ^J [ 5

= 0 .(10)

или

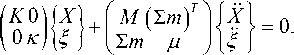
Для приведения системы (10) к симметричному виду, воспользуемся линейными комбинациями первых n строк (10) в соответствии с таблицей G : j , i

Система (8) описывает собственные колебания конечно-элементной модели L вместе с платформой. Если модель L получена путем закрепления свободной модели L , жесткости крепления платформы равны нулю, тогда частоты, найденные из решения проблемы (8), будут бл и зки к частотам колебаний свободной модели L . При этом формы собственных колебаний, найденные из (8), также будут близки к формам свободной модели, если их привести к одной системе координат с учетом относитель-

2 Г кх - ( s k ) T 5 + MX 1 = 0, G ^                         ^J

S k • X - SS k • 5 + S m • X = 0,

тогда с учетом (10) получим итоговую систему уравнений:

I K -(Sk)T UX+ IM 0 1Jc 1 (-Sk(к + SSk)J{5 } ( 0 (Ц -SSm)J[5'j

= 0. (11)

Получим выражение для SS m аналогично (5):

ного движения.

Переведем (8) в глобальную систему координат. Согласно (3) можно записать следующее:

X X X 0

.5 / = {5 О ),

^x 1 x 2 x 3 x 4 x 5

^x 6

...

1 x n - 3 x n - 2 x n - 1 x n x 0

y 0

...

Ю 3

x ₁ x ₂ x ₃ x ₄ x ₅ x ₆

...

И x n - 3 x n - 2 x n - 1 x n x о y 0 ...

№

x ₀ - A z 0 Ю 2 +A y ^ y ₀ + A z °to_x - Ax" ю . z ₀ - A y ° Ю 1 + A x" ю , to i ® 2

^Ю 3

...

z ₀ ® 1

® 2

^Ю 3 0 0

-A y N to i + A x N ® 2

...

Выразим локальные координаты X :

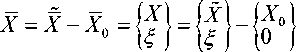
Подставим (9) в (8):

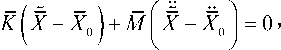
(^{к 0}^ / х 0! J M ( s m ) 1 J X I / X 0! I

⁽ 0 К Щ 5 / { 0 } J (s m ц J|_U J { 0 /

.

= 0,

так как ( S m ) T • 5 = M • X ₀ , ( S k ) T • 5 = K • X ₀, тогда I к -(s k) T 1 Cx\Jm 0\ J X I I 0      1 _n

.

( 0 К J 5 j \S т Ц 5 (S m • X ₀ J

Введем обозначение: S m • X₀ = SS m • 5 , тогда последняя система уравнений перепишется следующим образом:

A z ⁰( i> ₂ +A y °₃

J = a a x0

1 ...

a a

S m • X ₀ =

...

■ a

CDз v 11 ...u, n

.........

⁷61 ■■■ ^u 6 n J

	I	1		0		J 0		' 0		'A z 0		-A y 0	1
		0		1		0		-A z °		0 .		A x !0
		0		0		1		A y f		-A x j*		0
		0		0		0		1		0		0
		0		0		0		0		1		0
		0	■ ■	0	• •	0	• •	0	• •	0	• •	1	• •
= S m			■ x 0 +1	0	■ y 0 +1	0	' z0 +1	0	■ 0) t +1	A z 2 0	■ 0) 2 +1	-A y 2	■ (0 3
		0		1		0		-A z 2 0		0 .		A x 21
		0 0		0 0		1 0		A y 20 1		-A x 20 0		2 0 0
	(	... 0		... 0		... 0		... [ 0		... [ 0		... [ 0	J

Итак:

	N	N	NN	I Uc + 1 1 G i	N	I U 1	+ G i	N	I u	c + 0 G i
	У uc 1, G	2 u , G^	2 U L G „ 2	+ U L G i , A y 0 -	2	+ U G	A z 0 - i 1 i	2	+ u 1 G	A x 0 - 2 i
	, i = 1 N	, i = 1 N	= 1               i = 1 NN	( - U L G i ,A z 0 J I Uc + 2 G	i = 1 N	- U c ( 1 - G I U 2	A x 0 3 i c + G	i = 1 N	u u 2	A y 0 1 Zi J г + G
SS m =	2 U 2- G 1 i = 1	2 U2G,] i = 1	2 u2. , 2 = 1               i = 1	+ u c A y 0 - 2 G i 3     i - U c A z 0 2- G i ,2        i	2	+ U 2- G ( - U 2- G	A z 0 - i 1 i A x 0 ■ 3 i	2 i = 1	+ U 2 G U 2 G	A x 0 - i 2 i 1 A y 0

N

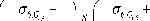
+ U c A y ⁰ - У + U r A z ⁰ 6- ^G i ,з       ¹                       6-^G i 1

-u_G A z ⁰    i = ' -a,_G A x ⁰

6- G i ,2      ¹ J (       ⁶- G i ,3     ¹

JJ

Аналогично можно получить выражения для SS k .

Необходимо отметить, что точка C не обязательно должна располагаться в центре масс, она может находиться в любом месте конструкции. Пусть точка C находится на расстоянии A X , A Y , A _Z от центра тяжести, тогда матрица ц может быть вычислена следующим образом:

	I 1	0	0	0	A Z		A Y      1
	0	1	0	-A Z	0		-A X
	0	0	1	A Y	-A X		0
	0	-A Z	A Y	J l+( a 2 -a x	) -A X A Y		-A x A z
Ц = m 0				m 0
	A z	0	-A X	-Ay Ay XY	J ^+ ( A 2 -a Y	)	-A y A z
					m 0	J 3
	A Y	-A X	0	-A x A г	-A y A z		+ ( A 2 -a z )
	(					m 0	J

где А ² = A X + А 2 + A Z .

Положение точки C влияет на относительные координаты каждого узла А х 0 , A y ⁰, A z 0 и матрицы к и ц . Более того, модель может быть закреплена не в одной точке, но нужно иметь в виду, что после процедуры освобождения по (8) или (11) появляется специфическая

f k + k ₂ — k ₂ — k ,

— k ₂ k ₂    0

_v — k , 0 k ₀ + k , ,

z*z

x

- x 2

. x 0

2 +

f m , 0

0 m ₂

_v 0 0 m ₀

— m ,

—

m 2 J

• •

~ x 1

~ x2 « « x0

= 0 .(14)

Система уравнений, описывающих собственные колебаний «Эквивалентной системы»

(рис.1), имеет вид:

погрешность, вызванная тем, что мы заменяем множество закрепленных степеней свободы всего 6-тью степенями свободы вектора ^ , что вносит определенные изменения в деформиро-

вание модели, а именно: все закрепленные точки относительно друг друга не деформируются. Другими словами потерянная информация о законах деформирования закрепленных точек не может быть восстановлена, поэтому освобожденная модель будет отличаться от исходной свободной модели.

Уравнения (8) и (11) могут быть использованы в преобразовании любых расчетных моделей, представленных в виде (1). Проиллюстрируем их применение на простейшем примере: колебания двух масс на пружинках (рис. 1).

Система уравнений собственных колебаний «Закрепленной системы» (рис.1) имеет следующий вид:

k , + k 2 — k 2

— k ₂   k ₂

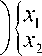
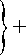
m ₁ 0 0 m ₂

• ■ x1

• ■ x2

= 0 . (12)

Преобразование (12) с учетом (8) приводит к следующей системе уравнений:

f k , + k ₂ — k ₂ 0 '

x

^{— k} 2

I ⁰

k ₂ 0 - x_:

0 k о J

x

f m i ⁰ m i )

■■    0 m 2 m 2

I m i m 2 m 0 J

' о,

■ ■ xi

- x ₂ ■ ■

I x 0 J

2 = 0 . (13)

Аналогичное преобразование, но с уче-

том (11), даёт такую

систему уравнений:

f k , + k ₂ — k ₂ — k , ^Л

— k ₂ k ₂     0

_v — k ,    0 k ₀ + k , _v

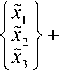
f m , 0 0 ) 0 m 2 0

( 0 0 m 3 J

• e

~

• •

~

- x₂

• •■

~ x 3

= 0. (15)

Очевидно, что так как ^:Х 3 = х ₀ , m 3 = m 0 - m 1 - m 2 , то система уравнений (15) совпадает с системой уравнений (14). Кроме того, следует отметить, что частоты собственных колебаний, найденные по уравнениям (13), совпадают с частотами по (14) и (15). При этом собственные формы колебаний, приведенные к глобальной системе координат, совпадают с соответствующими формами, определенными по (14) и (15). Если в (13)-(15) положить k ₀ = 0 , получим уравнения колебаний свободной системы.

ПРИМЕР ОСВОБОЖДЕНИЯ РАСЧЕТНОЙ МОДЕЛИ

На рис. 2 представлена условная балочная модель самолёта, стоящего на трёх стойках шасси.

Балки, имитирующие шасси, закреплены следующим образом: для задней опоры запрещены перемещения в трех направлениях и по углу рыскания самолёта, а для двух передних – только перемещения по вертикали.

Предлагаемый метод был реализован в виде программы Fortran, которая в качестве исходных данных использует матрицы жесткости и масс закрепленной расчетной модели, а также

Закрепленная система

Платформа, освобожденная система

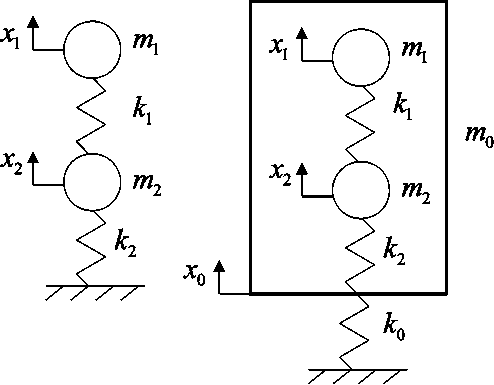
Рис. 1. Пример преобразования системы масс на пружинках

Эквивалентная система

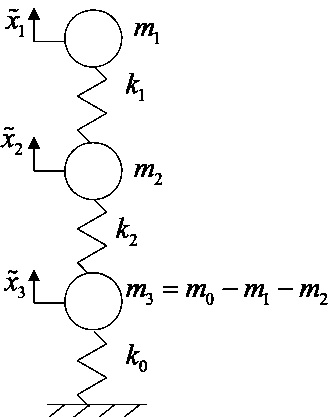
Рис. 2. Балочная модель самолёта информацию о массе и моментах инерции свободной конструкции. Результатом работы программы является матрицы жесткости и масс для свободной конструкции.

В табл. 1 приведены первые 30 частот собственных колебаний закрепленной модели, свободной модели и модели, освобожденной от закреплений по предлагаемому методу. В последней колонке показана разница в процентах между частотами свободной и освобожденной модели. Из представленных результатов следует, что частоты практически совпали между собой. Анализ форм колебаний освобожденной модели показал, что они также близки к формам колебаний свободной модели.

ЗАКЛЮЧЕНИЕ

Разработан метод освобождения математических моделей динамических систем, позволяющий восстановить расчетную модель свободного летательного аппарата после ее коррекции по результатам наземных модальных испытаний. Метод основан на том, что закрепленная модель ставится на виртуальную подвижную платформу, которая имеет инерционные характеристики исходной свободной конструкции. Это допускает движение модели, соответствующее движению абсолютно жесткого тела. Процедура осво-

Таблица 1. Результаты расчета

№ тона Частоты собственных колебаний, Гц Разница, % Закрепленная Свободная Освобожденная 1 1,85662 0 3,43958e-5 100 2 4,96444 9,28706e-5 6,42048e-5 -30,86637 3 6,17794 1,02634e-4 8,37633e-5 -18,38669 4 6,86614 3,49169e-4 1,00292e-4 -71,27698 5 13,10533 3,79388e-4 1,18879e-4 -68,66572 6 17,6852 4,14984e-4 1,36216e-4 -67,17566 7 20,03209 6,45900 6,45896 -5,25493e-4 8 21,06621 6,46460 6,46460 -6,91318e-5 9 23,86814 6,98969 6,98972 4,17216e-4 10 30,36936 21,27473 21,27574 4,74967e-3 11 47,42829 22,40967 22,40978 4,70805e-4 12 53,07032 25,32626 25,32857 9,12919e-3 13 67,18707 33,51995 33,51972 -6,87853e-4 14 71,56714 34,78906 34,78965 1,69555e-3 15 74,38522 36,34213 36,36089 0,05163 16 87,5522 58,08792 58,13280 0,07725 17 92,43276 60,88055 60,88067 2,03587e-4 18 99,24113 70,48880 70,50532 0,02344 19 113,88279 79,28135 79,36471 0,10515 20 121,82606 87,55269 87,55271 1,72603e-5 21 127,80676 92,35691 92,35987 3,20573e-3 22 135,72822 94,81595 94,81654 6,2726e-4 23 138,70894 120,28362 120,30526 0,01799 24 145,96664 135,00200 135,00525 2,40287e-3 25 154,73998 135,53758 135,54151 2,89958e-3 26 164,04692 142,63523 142,65131 0,01128 27 168,1857 146,64659 146,64601 -3,96758e-4 28 177,41973 167,78787 167,79104 1,89001e-3 29 244,28673 174,88687 174,90515 0,01046 30 263,15988 176,76258 176,76110 -8,34006e-4 бождения расчетной модели от закреплений не нарушает симметрии матриц жесткости и масс. На численном примере условной балочной модели самолета, установленного на шасси, показано, что освобожденная расчетная модель с высокой точностью воспроизводит частоты и формы собственных колебаний свободного самолета.