Метод отсечений с изменением структуры пространства для решения задач условной псевдобулевой оптимизации

В работах [1-3] был предложен метод отсечений для решения проблемы элиминации полного перебора при решении задачи нахождения локального экстремума произвольной псевдобулевой функции. Метод локального поиска - наиболее универсальный метод дискретной оптимизации - не гарантировал вырождения поиска в полный перебор пространства решений. А предлагаемый в работах [4; 5] подход не позволял находить решение задач с целевыми функциями, заданными алгоритмически или неявно.

Проблема исключения полного перебора была решена, но достаточно высокая оценка сверху метода отсечений делает очевидным стремление ее сократить. В схеме метода отсечений можно предположить две возможности сокращения оценки: через уменьшение числа отсекающих уровней и через сокращение мощностей этих уровней.

В работе [6] были исследованы возможности сокращения верхней оценки числа вычислений за счет выбора отсекающих уровней. Был предложен оптимальный способ выбора текущего отсекающего уровня. И хотя максимально возможное число отсекающих уровней не сократилось (и даже допускается их увеличение на один уровень), верхняя оценка числа вычислений значительно уменьшилась. При этом, в связи с доказательством оптимальности данного способа выбора отсекающих уровней, возможности для дальнейших исследований в этом направлении были исчерпаны.

Ниже будет исследована возможность сокращения верхней оценки числа вычислений за счет построения отсекающих уровней с меньшими мощностями. Предлагаемая модификация метода заключается в изменении структуры исследуемого на каждом этапе подпространства через его разложение на уровни новой произвольной точки. При этом новой точкой выбирается та, которая имеет наибольшее число своих уровней в текущем подпространстве. Тем самым достигается представление множества точек подпространства большим числом уровней с меньшими мощностями.

Свойства пространства булевых переменных. Приведем необходимые определения и утверждения, принятые и доказанные в [7].

Определение 1. Псевдобулевой функцией называют вещественную функцию на множестве булевых переменных: f : B 2 ^ R , где B 2 = {0,1} , В " = В 2 х В 2 х ... х В ₂ .

Общая постановка задачи псевдобулевой оптимизации имеет вид:

f (X) ^ extr , где f : S ^ R , S с B22. Если S = B*2, то постановка соответствует задаче безусловной оптимизации.

Определение 2. Точки X , Y е B ₂ ” назовем к-соседни-ми, если они отличаются значением к координат, к = 1, n ; 1-соседние точки будем называть просто соседними.

Отсюда следует, что две точки X , Y е B 2 являются к- соседними, если n

Я x j ^- y j\ = ^к .

j =1                                    _____

Определение 3. Множество O k ( X ) , к = 0, n , всех точек B * 2 , к-соседних к точке А, назовем к-м уровнем точ- киХ. При этом O ₀ ( X ) = X .

Лемма 1 [7]. V X е B 2 :card O k ( X ) = C 2 , где C 2 - число сочетаний из и по к.

Лемма 2 [7]. V X е B ₂ ⁿ л V X ² е O k ( X ) , к = 0, 2 : card { O 1 ( X^k ) n O k - 1 ( X )} = к , card { O ( X^k ) n O k _{+ 1} ( X )} = n - к .

Лемма 3 [7]. V X е B ₂ ⁿ : B ₂ ⁿ = U O₂ ( X ) .

к =0

Как следует по лемме 3, пространство B 2 всегда можно представить в виде объединения и уровней произвольной точки X е B 2 , которую в дальнейшем будем обозначать X ⁰. При этом любой уровень O₂ ( X °), к = 1, n - 1 разбивает пространство B 2 на два непустых непересека-ющихся подпространства, состоящих из объединения полных уровней X ⁰:

к -1                             n

V 1 =и O i ( X ⁰), V 2 =u O i ( X ⁰) .

i =0                           i = к +1

И, по лемме 1, на каждом к-м уровне точки X ⁰ лежит ровно С к точек.

Нетрудно видеть, что в соответствии с формулой С р = с П - ^к пространство B 2 , разложенное на и + 1 уровней точки X ⁰ , представляет собой симметричную фигуру относительно среднего уровня с номером и / 2 (при четных значениях и ) или уровней с номерами Р n /2^- | , Р п / 2" | - 1 (при нечетных и). Причем в связи с биномиальным распределением точек B 2 по уровням большая часть всех точек пространства сосредоточена в средних уровнях X ⁰ .

Точку X ⁰ будем называть центром структуры пространства булевых переменных и говорить о разложении B 2 2 по уровням этой точки.

Метод отсечений. Обозначим через X * точку B 2 , определяемую по условию f ( X₂ ) = min f ( X ) . Иначе X е O * ( X ⁰)

говоря, точка X * доставляет минимум функции_/(Х) на к-м уровне X ⁰ . При этом она может быть не единственной.

Лемма 4[1]. ЕслиДХ - унимодальная на B2 функция и для некоторого X е O1 (X* ), к = 1, n -1, выполняется f (X) < f (X*k), то точки X и X* принадлежат одному подпространству: B2n - ^ или К2.

Лемма 5 [2]. Если для унимодальной на Bn функции /(X для некоторых точек Xi, X2 е Ok (X0) выполняется f (Xi) < f (Xk-i), f (X2) < f (Xk+i),то X* опРеделяется по условию f (X*) = min{f (X1), f (X2)}.

На основании лемм 4, 5 и строится метод отсечений для задачи безусловной оптимизации унимодальной разнозначной функции. Под разнозначностью функции будем понимать отсутствие различных точек в пространстве решений, значения функции в которых совпадают. Необходимо отметить, что условие разнозначности функции везде можно заменить более слабым ограничением на вид функции: для любой точки X е B ₂ ⁿ (кроме точки минимума) должна существовать хотя бы одна соседняя к ней точка Y е B n , в которой/(К) (Х). Такое условие допускает наличие множеств постоянства.

Приведем общую схему метода отсечений.

• 1.    На первом этапе пространство решений B n делим на два подпространства некоторым уровнем O k ( X °), k = 1, n - 1 .Он назван отсекающим уровнем.

• 2.    Вычисляем значения функции в точках отсекающего уровня и делаем заключение, в каком из исследуемых подпространств находится минимум. Если минимум находится на отсекающем уровне, то останавливаем поиск и переходим к конечному пункту схемы.

• 3.    Подпространство, в котором находится минимум, опять делим на два подпространства новым отсекающим уровнем и переходим к п. 2 схемы.

• 4.    Останов.

Подробное описание метода отсечений для задачи безусловной оптимизации приводится в [2].

Заметим, что деление подпространств на два проводится до тех пор, пока подпространство, содержащее^ * , не будет состоять из одного уровня (если, конечно, до этого не будет определен минимум). На этом последнем уровне и лежит точка, доставляющая оптимальное значение функции. При этом в соответствии с леммой 5 этот последний уровень проверять не стоит.

Выбор отсекающих уровней. Очевидно, что лучшую оценку снизу будет иметь алгоритм, начинающий свою работу с маленьких по мощности уровней. В частности, не улучшаемая оценка снизу будет у алгоритма, стартующего с нулевого уровня точки X ⁰ . И она будет равна и + 1 (сама точка плюс ее 1-окрестность). Поэтому этот шаг может быть первым у всех алгоритмов выбора отсекающего уровня, что делает оценку снизу минимальной. Однако такая оценка не представляет никакой практической ценности, и все внимание в дальнейшем будет уделено сокращению верхней оценки числа вычислений и оценки в среднем.

При отсутствии априорных сведений о функции естественно рассматривать средние уровни на каждом этапе алгоритма, а в качествеХ - нулевую точку. Под средним уровнем на этапе можно понимать уровень с номером, равным среднему арифметическому номеров граничных уровней (целой части), или же уровень, разбивающий исследуемое на этапе подпространство на два равномощных (максимально близких по мощностям).

В работах [1; 2] предлагаются именно эти два алгоритма выбора отсекающего уровня. Им соответствуют два алгоритма метода отсечений: алгоритм 1 (разбиение по арифметическому среднему) и алгоритм 2 (разбиение по мощностям). Доказывается, что уже при малых значениях и алгоритм 1 превосходит полный перебор в несколько раз и при росте и эта разница возрастает. Также показано преимущество второго алгоритма перед первым.

Но отсекающие уровни алгоритма 2 тоже не обеспечивают оптимального (в смысле верхней оценки числа вычислений) разбиения исследуемого подпространства. Поэтому в [6] был предложен алгоритм 3, имеющий верхнюю оценку числа вычислений лучше, чем алгоритм 2. При этом была доказана оптимальность стратегии выбора отсекающих уровней, реализованной в алгоритме 3.

Свойства подпространств B П . Дадим определения пути между двумя точками и связности множества точек пространства булевых переменных.

Определение 4. Множество точек W ( X ⁰, X ¹ ) = { X ⁰, X ¹ ,К , X ¹ } с B n назовем путем меж-дуточками X ⁰ и X¹ , если V i = 1, ..., /точка X ¹ является соседней к X ^{1 - 1} .

Определение 5. Множество A с B П назовем связным множеством, если V X ⁰, X l е A существует путь W ( X °, X l ) с A .

Из всех подпространств B ₂ ⁿ выделим подпространства, представляющие собой отдельные уровни некоторой точки X ⁰ или части уровней.

Лемма 6 [3]. Любая точка X е O m ( X ⁰), m = 1, n - 1 , имеет только 2к-соседние к себе точки, лежащие на этом же уровне точки X ⁰ . При этом число 2к-соседних к X точек, лежащих на m-м уровне X ⁰ , определяется форму ^лой C m C k _ _m ^, k = 1, min { m , n - m} .

По леммам 1, 6 следует, что множество всех точек m-го уровня точки X0 е Bn может быть представлено как объединение всех 2к-соседних точек произвольной l точки X е Om(X0). При этом Cm = £ CmCk-m , где l = min{ m, n - m}.                      k=0

Следствие I. Подпространство, представляющее собой уровень некоторой точки X ⁰ е B ₂ ⁿ или любую его часть, состоящую более чем из одной точки, является несвязным множеством.

Доказательство. Непосредственно следует по лемме 6 и определению связности множества.

Определение 6. к-м условным уровнем (или к-м подуровнем) точки X m е O_m ( X ⁰) назовем множество всех точек, 2к-соседних к X m и лежащих на m-м уровне точки x ⁰ . Обозначим это множество о * ( x ⁰, x m ) = O m ( x °) п о 2 * ( x m ) .

В соответствии с этим определением и леммой 4 любой к-й условный уровень точки Xm е Om (X°) (к = 1, min{m, n - m} -1) разбивает множество Om (X0) на два непустых непересекающихся подпространства, состоящих из объединения полных условных уровней точки X0: m к-1                              min{ m, n - m}

V1 ^m = и O ( X°,x m ) , V m =   U    O 1 ( X °, x m ) .

i =0                                      i = к +1

Заметим, что в соответствии с леммой 6 максимальное число условных уровней на m-м уровне точки Xm равно min{m, n - m} и не может превосходить и/2, причем достигаться значение и /2 может только на среднем уровне точки X0 для четных значений и. И, в отличие от распределения точек B2 по уровням точки x0, распределение точек на ее т-м уровне уже не будет симметричным относительно какого-либо условного уровня, кроме случая когда т = и/ будет 2, а и - четное.

Лемма 7. V X е O_m ( X ⁰), m = 0, n , имеет только четное соседст во со всеми точка ми уровне й O m -2 k ( X ⁰)( k = 0, L m / 2 J ) , O m ₊₂ k ( X ⁰)( k = 1, L ( n - m )/2J) и не четное соседс тво с точками уров ней O m _{-(2 k -1)} ( X " ) ( k = 1, L ( m + 1)/2 j ) , O m +(2 k —i) ( X ⁰) ( k = 1, L ( n - m + 1)/2 j ) .

Доказательство. В соответствии с леммой 6 любая точка X е O_m ( X ⁰), m = 0, n , имеет на этом уровне только четное соседство. А по лемме 2 следует, что все соседние к ней точки лежат на двух ближайших уровнях с номерами т - 1, т + 1. Отсюда, с учетом связности пространства B ₂ ” , делаем заключение о справедливости утверждения.

Лемма 8. V X ⁰ е O ( X ⁰) :

mm card {O2 , (Xm) n Om - k (X °)} = Cm+ kCn - m

(k- четное, 0 <  k < т; i = k ,min { m - k , n - m + k } );

card { O 2 i -1 ( X m ) n O_m - k ( X °)} = C m^{k - 1} C n -m

(k- нечетное, 1 <  k < m; i = k ,min { m - k + 1, n - m + k } );

card { O 2 i ( X m ) n O m + k ( X °)} = C m ^- k C n + m

(k- четное, 0 <  k < и-т; i = k ,min { m + k , n - m - k } );

card{0₂ ,(A>0 (A)' = C^{i - k}C ^{+ k -1}

2 i -1 m       m + k V              m n - m

(k-нечетное, 1 < k < и-т; i = k ,min { m + k , n - m - k + 1 } ). Доказательство. Справедливость формул следует по леммам 6,7 и комбинаторным подсчетам. Для более удобного подсчета за точку X ⁰ следует взять нулевую точку, а за X m - точку с единицами на первых т позициях.

Следствие 2. Произвольный четный уровень точки 00

X m пересекается только с четными уровнями X , алю-бой нечетный - только с нечетными уровнями X ⁰ .

Доказательство. Следует по леммам 7, 8.

Следствие 3. Справедливы формулы:

С2i =У Ci+kCi-k W

K

C "" ¹ = 1 C m ^{+ k - 1} C n-km (0 <  i <  ( n + 1)/2) .

k =0

Здесь К - максимально возможное значение k, зависящее от заданных и, т, i.

Доказательство. Следует по формулам лемм 1,8.

Лемма 9. Множество точек любого связного множества V е B n всегда располагается на / последовательных уровнях произвольной точки X е B 2 , l = 1, n + 1 .

Доказательство. Если множество состоит из одной точки, то утверждение очевидно. Поэтому будем считать, что связное множество V состоит более чем из одной точки.

Предположим противное: некоторые точки множества V лежат на двух уровнях произвольной точки X ' е B ₂ ⁿ с номерами i, 7 + 2, а на уровне с номером 7+1 нет ни единой точки из V.

Не нарушая общности суждений, за точку X' е B2n можно взять точку с нулевыми координатами. Тогда все точки, лежащие на i-м уровне точки X', будут иметь ровно i единичных компонент, а лежащие на ее (7 + 2)-м уровне - на две единицы больше. Таким образом, точки этих двух уровней будут отличаться как минимум на две компоненты и, следовательно, не могут быть соседними друг к другу. То есть множество V не является связным, что противоречит условиям леммы.

Следствие 4. Леммы 4,5 справедливы для любой унимодальной разнозначной функции/(А'), определенной на связном множестве V е B n .

Доказательство. Следует по леммам 4, 5, 9.

Из следствия 4 вытекает, что метод отсечений можно использовать для любых задач условной оптимизации, множество решений которых представляет собой связ ное множество.

Метод отсечений с изменением структуры пространства. Результаты исследования свойств пространства B ₂ ⁿ и его подпространств, приведенные в данной статье, позволяют модифицировать метод отсечений и существенно сократить верхнюю оценку числа вычислений. Эта модификация названа авторомметодом отсечений с изменением структуры пространства и впервые была применена для решения задачи безусловной оптимизации. Полученные оценки показали эффективность тактики изменения структуры пространства, поэтому целесообразно применять ее и для задач условной оптимизации.

На основании леммы 9 автор исследовал возможность разложения образующегося на каждом этапе подпространства по уровням другой точки BTn, не обязательно принадлежащей этому подпространству, и сечения подпространства некоторым средним уровнем новой точки. Цель состоит в том, чтобы на каждом этапе строить средние сечения с наименьшими мощностями, добиваясь сокращения верхней оценки числа вычислений. Таким образом, модификация метода отсечений заключается в изменении структуры исследуемого на каждом этапе подпространства.

Рассмотрим сначала хорошо известную задачу условной псевдобулевой оптимизации с ограничениями вида

S =

n

X е B 2 : n ₁ <  1 x j <  n ₂ ; n ₁ >  0, n ₂ <  n > .

j =1

Эта постановка соответствует задаче «на уровнях»,

• т. е. когда множество допустимых решений состоит из одного или нескольких уровней нулевой точки. При n ₁ = 0, n ₂ = n имеем случай безусловной оптимизации.

Нетрудно заметить, что для малого числа уровней (особенно при значениях n1, n2, близких к и /2) метод отсечений становится малоэффективным. Так, если пространство решений состоит из трех уровней точки X0, то вер хняя оценка числа вычислений превосходит половину точек множества, а для одного или двух уровней вырождается в полный перебор. Таким образом, целесообразно представить один, два или три уровня точки X0, образующие пространство решений, в виде большего числа уровней (или частей уровней) какой-либо другой точки X е B2.

Предположим, что пространство решений состоит из двух или трех мощных уровней точки X0 с номерами fn/2]-1, Г n/2J- 2 или Гn/2J-1,Гn/2]-2,Гn/2]-3 , т. е. мы имеем худшие по числу вычислений случаи для метода отсечений. Случай с одним уровнем опускаем, так как он подробно исследован в работе [3].

Рассмотрим сначала случай, когда исследуемое подпространство состоит из двух уровней. В соответствии с методом отсечений в худшем случае необходимо будет исследовать оба уровня, т. е. вычислить значения во всех точках множества решений. Таким образом, верхняя оценка числа вычислений будет / 1 = С\n ^{/2 ] 2} + d_nn ^{/2 ]} 1 , а оценка снизу - С" ^/2 ^^{- 2} + Р п /2 J - 2 .

Изменим структуру пространства решений, разложив его по уровням некоторой точки X р ° _{к /2} j_{- 2} е O р n _/2^_-2 ( X ° ) , которую будем называть новым центром структуры пространства B ₂ ^к . По лемме 8 k-й уровень точки X 0 _{к /2}^_-2 может пересечь только один из двух уровней точки X ⁰ : либо с номером Р к /2 ]- 1 , либо с номером Р к /2 ]- 2 . Первый случай, по следствию леммы 6, возможен только при нечетных значениях k, а второй - только при четных.

В соответствии со схемой метода отсечений будем брать такой уровень точки X р ⁰ _{к /2}]_-2 , который разбивает исследуемое подпространство на два максимально близких по мощности подпространства. Возьмем в качестве отсекающего уровня средний уровень точки X р ⁰ _{к /2}^_-2 с четным номером и обозначим его через k 1 . В дальнейшем в качестве отсекающих уровней также будем брать уровни с четными номерами, которые обозначим k ₂ , k ₃ , ..., k_t . Нетрудно заметить, что в этом случае пересечения всех четных уровней X р ⁰ _{к /2}^_-2 с уровнем Р к /2 ] - 2 образуют множество условных уровней точки X р ⁰ _{к /2}^_-2 на уровне Р к /2 ] - 2 . При этом число условных уровней X р ⁰ _{к /2} j_{- 2} в соответствии с леммой 8 равно min{ P к /2 J- 2, Р к /2 J + 2} + 1 = Р к /2 J- 1 , с учетом самой точки X Р0 _{к /2}^_-2 как нулевого уровня ее самой.

В худшем по числу вычислений случае точка минимума X * должна лежать на уровне X р ° _{к /2}^_-2 с номером k 1 - 1 или k 1 + 1 . Пусть это будет номер k, - 1 . Тогда оценка сверху числа вычислений значений функции для нахождения локального минимума в подпространстве, состоящем из двух уровней с номерами Р к /2 ]- 1, Р к /2 ]- 2 , не превзойдет значения

B = V C_r^k ' /2₁ С^х   „+ t ( к - (Р к /2] - 2)) =

| к /2|-2 к -(| к /2|-2)       ^v М I ⁷⁷

i =1

t

= TC'rn С м2|₊₂ + 1 (I к /2 1 + 2) | к /2|-2 р к /2J+2                   J ⁷.

=1

Здесь t - число отсекающих уровней с номерами k 1 , k 2 , ..., k, , t = p iog ₂ ( P к /2 J- 1) J + 1 .

Так как в оценке В участвуют мощности только несколько условных уровней точки X р ° _{к /2} j_{- 2} , то ее преимущество перед оценкой А = с\ ^{к /2 J- 2} + С ^{к /2 J- 1} , включающей мощности всех условных уровней двух уровней, очевидно. Оценим это преимущество через отношениеА / В.

Используем для этого выражение для приближенного вычисления d\к2', полученное в [3] при помощи фор мулы Стирлинга:

а =        d; ^{/2 J- 2} + d; ^{/2 J- 1}         >

B S C k /2 j- 2 c k /2 j+ 2 + , ( Р к /2 J+ 2)

i =1

2 С Р к /2J-2

_r (Р к /2]-2)/2_г(Р к /2]+2)/2 ^tC Р к /2]-2     C р к /2j+2

2 с [^{к /2 ]- 2}

_г (Р к /2]-2)/2_г(Р к /2J+2)/2 ^,С Р к /2J-2     C р к /2J+2

, Р к /2 ]- 4/ Р к /2 ]

>а(к) P J P J.

p iog 2 Р к /2 J- 1 J + 1

( Р к /2 ]- 1) Р к /2 J

Здесь б( к ) = 1,8             р----, и уже при

( Р к /2 J + 1)( Р к /2 J + 2)

небольших и значение б( к ) близко к 1,8.

Таким образом, отношениеА /В неограниченно растет с увеличением и. Так, например, для и = 100 при выборе отсекающих уровней по принципу арифметического среднего, А / В = 4,68. То есть в самом трудном случае нахождения экстремума и при худшем алгоритме выбора уровней число вычислений при разложении пространства решений по уровням новой точки сокращается бо лее чем в четыре раза.

Что касается оценок снизу, то для метода отсечений она, как было отмечено ранее, равна D = с к" ^{/2 ]- 2} +р к /2 j + 2 . В методе с изменением структуры пространства нижняя оценка не превосходит значения E = С * к к 22 С р ⁽ к к 2 22 2 +Р к /2 J + 2 . Отношение оценок находим по схеме, приведенной выше для верхних оценок.4,В:

> б( к )

D           С ^{Р к /2 J- 2}

— > --;--;--- > р г (Рк/2j-2)/2r( Рк/2]+2)/2

C Р к /2]-2 C р к /2J+2

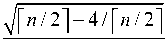
Для и = 100, например, это отношение превосходит 5,8.

Мы проанализировали случай, когда исследуемое пространство состоит из двух уровней точки X0. Если рассмот реть вариант с тремя уровнями, то получим, как нетрудно заметить, такое же значениеВ и оценку отношенияА / В:

A

B

С Р к ^/2 ]-1 ₊ с Р к ^/2 J- ³ B

О Z~' Р к /2]-2

> ^ C^— B

>

> б( к )

Р к /2 J- 4/ Р к /2 ] Р 1од 2 Р к /2 J- 1 J + 1

Здесь было использовано свойство выпуклости функции C m (как функции от т) при значениях т, близких к и [6].

Заметим, что в обоих рассмотренных случаях уже после первого сечения можно было заменить центр структуры на новый, который раскладывал бы образованное подпространство на большее число уровней, чем прежний центр. В этом случае верхняя оценка числа вычислений сократилась бы еще больше.

Если подпространство решений состоит более чем из трех последовательных уровней точки X0 или представляет собой произвольное связное множество точек B"^, то для сокращения нижней и верхней оценок числа вычислений также следует придерживаться тактики выбора центра структуры. Естественно, будут возникать ситуации, когда целесообразно изменять структуру исследуе мого подпространства несколько раз, в зависимости от результатов отсечений.

В соответствии с леммой 9 и следствием из нее метод отсечений с изменением структуры пространства реше- ний будет гарантировать элиминацию полного перебора и эффективное решение задачи, вне зависимости от вида ограничений.

В самом общем виде схема метода отсечения с изменением структуры пространства для задачи условной псевдобулевой оптимизации может быть записана следующим образом:

• 1.    Определяем точку X_c е B 2 , имеющую наименьший по мощности средний уровень на множестве допустимых решений.

• 2.    В качестве отсекающего берем средний уровень точки X_c и вычисляем значения во всех его точках.

• 3.    По условию леммы 4 делаем заключение, в каком из двух образованных подпространств находится минимум:

• -    если минимум находится на отсекающем уровне, то останавливаем поиск и переходим к п. 5 схемы;

• -    если подпространство, в котором находится минимум, состоит из части только одного уровня точки X_c (кроме первого и нулевого), то определяем минимум из условия леммы 5 и переходим к п. 5 схемы.

• 4.    Множеством допустимых решений объявляем подпространство, в котором находится минимум, и переходим к п. 1 схемы.

• 5.    Останов.

Итак, в схеме метода отсечений с изменением структуры пространства решений самым важным и сложным этапом является выбор оптимального сечения на этапе - это п. 1 схемы. В соответствии с ним в качестве центра структуры следует выбирать точку с наименьшим пересечением точек ее среднего уровня с множеством решений. Поэтому при известной структуре множества решений в качестве нового следует выбирать центр структуры, имеющий наибольшее число уровней в исследуемом пространстве.

Нетрудно заметить, что эта задача эквивалентна задаче нахождения диаметра множества решений, под которым будем подразумевать наибольшее соседство между двумя точками пространства решений, т. е. на каждом этапе необходимо решать задачу n

Z К- ^ ^ max, i=1

• X , Y е S с B 2 .

А после нахождения двух самых отдаленных точек остается выбрать одну из них в качестве нового центра структуры.

Конечно, существуют множества допустимых решений значений, имеющие специфические конфигурации, для которых выбор среднего уровня в качестве отсекающего не является оптимальным. В этом случае, при знании свойств пространства допустимых решений, стоит попытаться определить его наиболее узкие места и строить сечения с учетом специфики множества.

В заключение сделаем несколько замечаний:

• -    схема метода отсечений с изменением структуры пространства для задач условной псевдобулевой оптимизации включает как частный случай схему метода для задачи безусловной оптимизации;

• -    для задачи безусловной оптимизации можно построить конкретный алгоритм (или алгоритмы) нахождения центров структуры, в зависимости от местоположения X * и размерности задачи, а также определить ниж

нюю и верхнюю оценки числа вычислений. Для задачи «на уровнях», рассмотренной выше, это также возможно. Для произвольной же задачи условной оптимизации в каждом конкретном случае необходимо знать структуру пространства решений, чтобы оценить затраты на поиск;

• -    метод отсечений с изменением структуры пространства совпадает с методом отсечений без изменения структуры в случае если в первом методе центр структуры определять единственный раз на первом этапе поиска (без дальнейшего изменения структуры пространства решений), а также при таких множествах допустимых решений, когда определенный на первом этапе центр остается оптимальным на всех последующих этапах;

• -    хотя метод отсечений с изменением структуры пространства работает для задач условной оптимизации со связным множеством допустимых решений, его также можно использовать и для задачи «на уровнях», когда точки уровня образуют несвязное множество. В работе [3] для такой постановки задачи доказывается возможность использования метода отсечений.

Результаты исследования свойств пространства булевых переменных и его подпространств позволили разработать метод отсечений с изменением структуры пространства, который явился обобщением метода отсечений, предложенного ранее автором для решения задач условной и безусловной псевдобулевой оптимизации. Данный метод имеет преимущество перед методом отсечений: на классе задач условной псевдобулевой оптимизации с унимодальной разнозначной целевой функцией нижняя и верхняя оценки числа вычислений могут сокращаться во много раз.