Метод параметрической оптимизации процесса принятия решений в системах распознавания текстовых меток на видеоизображениях

В настоящее время распознавание текстовых меток на видеоизображениях является одной из важных прикладных задач компьютерного зрения. Обычно оно применяется для идентификации движущихся объектов контроля, имеющих регистрационные надписи. Примерами таких объектов могут служить наземные транспортные средства, грузовые контейнеры, промышленные изделия и др.

Распространение систем распознавания текстовых меток (СРТМ) выявило проблему, связанную со сложностью настройки параметров алгоритмов СРТМ для наиболее эффективного функционирования в заданных условиях эксплуатации. Сложность заключается в том, что алгоритмы СРТМ, как правило, весьма нетривиальны и обладают большим количеством настраиваемых параметров, каждый из которых принимает значения из определенного диапазона. Конкретный набор значений параметров алгоритма будем называть конфигурацией. Количество конфигураци й часто чрезвычайно велико, что существенно затрудняет поиск такой конфигурации, которая бы обеспечивала требуемые значения критериев эффективности СРТМ. На современном этапе эта трудоемкая работа, как правило, производится разработчиками вручную, исходя из опыта, интуиции и знания алгоритмов. Это усложняет разработку и удорожает такие системы , ограничивая их применение. Поэтому важной задачей является создание новых методов и средств параметрической оптимизации алгоритмов СРТМ с учетом заданных условий эксплуатации.

Известен подход, при котором с целью повышения эффективности распознавания текстовой информации межд у алгоритмами передаются списки возможных решений, что позволяет снизить вероятность потери исти нного решения на промежуточных этапах анализа изображения [3]. Каждому решению сопоставляется некоторая численная оценка его правдоподобия, список решений упорядочен по убыванию оценок правдоподобия.

Чем больше элементов допускается в списке, тем выше вероятность того, что он содержит верное решение, но при этом увеличивается время анализа и возрастает вероятность ошибки второго рода. Отсюда возникает задача усечения списка либо его отклонения согласно выбранным порогам на длину списка и оценку его правдоподобия. В статье описывается метод поиска оптимальных значений порогов, а в качестве экспериментальной базы выбрана система распознавания идентификационных номеров железнодорожных вагонов.

1. Алгоритмы системы распознавания текстовых меток на видеоизображениях на примере идентификационных номеров железнодорожных вагонов

Основная часть алгоритмического обеспечения систем распознавания текстовых меток реализуется в виде отдельного программного модуля – модуля распознавания. Он представляет собой последовательность взаимосвязанных алгоритмов. В общем случае модуль распознавания состоит из алгоритмов локализации текстовой метки (далее под текстовой меткой понимаем ее графический образ), сегментации локализованных зон изображения, распознавания сегментов и принятия решений. Ввид у неопределенности условий формирования входных изображений, создание алгоритмов, гарантирующих правильное решение, затруднено. Поэтому на практике применяются эвристические алгоритмы, ответы которых являются правильными с некоторой вероятностью.

Алгоритм локализации (АЛ) производит поиск зон – прямоугольных фрагментов изображения, предположительно содержащих образ текстовой метки. На вход модуля могут поступать изображения I m _x n двух видов: информативные и неинформативные. Информативные изображения, в отличие от неинформативных, содержат образ текстовой метки. На рис. 1 представлены примеры входных видеоизображений (кадров с разрешением 288 x 384).

б)

Рис. 1. Примеры входных видеоизображений

(а – неинформативное; б – при дневном освещении; в – при ночном освещении)

На первом этапе локализации рассчитывается матрица оценок правдоподобия принадлежности каждой точки образу текстовой метки: E_m>n , где E ij -оценка правдоподобия принадлежности пикселя с координатами i , j образу метки. Матрица E mn является исходными данными для поиска зоны, содержащей текстовую метку. Рассмотрим метод ее построения.

В теории обработки изображений одним из основных методов преобразования изображений к виду, удобному для анализа, является применени е фильтров. Реализуем вычисление матрицы E_{m x n} как наложение фильтра H D _х D :

Е- ■ = i , j

i + d   j + d

2   2 i k i, k 2

k 1 = i - d k 2 = j - d

' ^Hk 1 - i + 1, k 2 - j + 1

э i D-1

Здесь d = —2— определяет размер фильтра, который представляется в виде квадратной матрицы с нечетным количеством элементов в строке (столбце).

Как правило, особенным свойством участка изображения, содержащего текстовую метку, по сравнению с другими участками, является высокий уровень градиента (перепадов яркости). Поэтому в роли фильтра можно взять, к примеру, матрицу, применение которой позволяет вычислить величину перепада яркости в заданной окрестности и направле- нии, например:

Г-1 0 П н = -10 1

I - ^{1 0} 1 )

На рис. 2 представлен результат наложения фильтра (2) на изображение железнодорожной цис- терны с идентификационным номером на борту.

Рис. 2. Результат наложения фильтра

Представим матрицу Emхn в виде последова тельности столбцов шириной 5= n parts

элемен-

тов, где parts – параметр АЛ. Для каждого столбца строится ф ункция среднего значения оценки правдоподобия в строке:

5 *( k + 1)

A i , k = - 2 E j ⁵ j = s * k

EA i , k =

1 h

i + h - 1

2 A , k j = i + 1

0.5( A i , k + A i + h , k )

По результатам ан ализа каждого столбца формируется зона, попадающая в список решений АЛ. Из (4) определяются координаты k -ой зоны SZ ^k :

y(k) = e = arg max EAi,k , i=1.. m x1(k) = max{ks - (w - s),0},

У 2 k ) = У 1 ⁺ h ,

x 2 ^k ) = min{( k + 1) s + ( w - s ), n - 1}, где h - высота текстовой метки, w – ширина. Координаты x ₁, x ₂ рассчитываются с некоторым «запасом» x 2 — ^x i >  w , а также с учетом возможного выхода за пределы границ изображения (0, n - 1). Оценкой правдоподобия зоны является EA _{e , k} .

Алгоритм сегментации (АС) производит поиск сегментов – координат предполагаемых символов на локализованной зоне. На первом этапе сегментации вычисляются оценки правдоподобия принадлежности пикселей линиям символов, в простейшем случае используются готовые результаты наложения фильтра H либо непосредственно яркость пикселей. Результатом первого этапа является массив оценок правдоподобия EZ _{h х} w .

Второй этап – это вычисление вектора средней оценки правдоподобия по столбцам:

h

Ai = - TEZt i .                           (5)

j                           i,j h i=1

Вектор A позволяет обнаружить промежутки фона между символами, которые проявляются в виде экстремумов (рис.3).

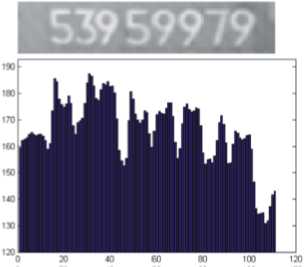
Рис. 3. Вектор средней оценки правдоподобия по столбцам локализованной зоны

На третьем этапе производится обнаружение вертикальных разделителей – границ межд у символами Dev . Для этого каждому элементу A_i сопоставляется оценка правдоподобия H_i . Чем выше эта оценка, тем выше вероятность, что в данном месте находится промежуток фона межд у символами. Индексы i выбранных H_i – это координаты вертикальных разделителей (границы) межд у символами: Dev = { dev₁,dev 2 ,...,dev_k }, где k - количество найденных разделителей.

На четвертом этапе осуществляется уточнение вертикальных и горизонтальных грани ц символов. Для этого методом Отсу вычисляется пороговое значение яркости для фрагмента изображения между двумя разделителями. Порог позволяет бинаризовать фрагмент и в результате найти координаты выделенного на фрагменте объекта. Оценкой правдоподобия сегмента является отношение его самого яркого пикселя к самому темному. Сегменты, упо- рядоченные по убыванию оценки правдоподобия, образуют список решений АС .

Алгоритм распознавания (АР) производит распознавание (классификацию) изображений отдельных сегментов. Сегмент, отнесенный к одному из классов символов, называем распознанным, а отнесенный к классу шумов – нераспознанным. АР реализован в виде многослойного персептрона, обученного классифицировать изображения символов. Выход нейронной сети есть оценка правдоподобия принадлежности изображения конкретному классу символов. На данном этапе не производится формирование списка решений, поскольку это приводит к комбинаторному взрыву количества решений, формируемых по результатам распознавания сегментов зоны, и при этом, возможно, имеет смысл лишь при наличии априорной информации о кодах текстовых меток.

Множество распознанных сегментов анализируется алгоритмом формирования решений (АФР), который производит поиск всех возможных последовательностей распознанны х сегментов, потенциально являющихся образами символов метки (решениями). Такие последовательности образуют список решений, упорядоченный по убыванию оценки правдоподобия, которая рассчитывается как сумма оценок правдоподобия соответствующих распознанных сегментов.

АФР реализован на основе алгоритма поиска в глубину. Исходными данными для такого поиска является матрица смежности сегментов, которая содержит информацию о парах сегментов, потенциально являющихся изображениями соседних символов метки. При отсутствии какой-либо априорной информации о текстовых метках, например, списка текстовых меток, в качестве итогового выбирается решение, обладающее максимальной оценкой правдоподобия.

2.    Задача параметрической оптимизации алгоритмов управления списками решений

В работах [1-3] с целью повыш ения эффективности распознав ания текстовой информации предложено передав ать межд у алгоритмами списки решений, что позволя ет снизить вероятность потери истинного решения на промежуточных этапах анализа изображения . Каждому решению сопоставляется н екоторая численная оценка его правдоподобия, которая используется для упорядочивания списка и последующего усечения списка либо его отклонения как вероятно неинформативного [2]. Список решений некоторого алгоритма мод уля распознавания анализируется алгоритмом усечения списков (АУС). Для этого используются два порога: K и E . Решение о принятии или отклонении списка выполняется согласно результату срав нения оценки правдоподобия списка с по рогом E . Далее пред полаг аем, что параметры E целочисленные и принимают значения из некоторого ограниченного диапазона. Порог K ограничивает д лину принятого списка.

Обозначим параметры АУС алгоритмов локализации, сегментации, распознавания и формирования решений, соответственно, { K L , E L }, { K S , E S }, { K K , E _K }, { K R , E R }. На рис. 4 показан пример -структурная схема модуля распознавания с алгоритмами усечения списков.

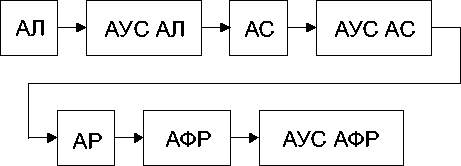
Рис. 4. Структурная схема модуля распознавания с алгоритмами усечения списков

Чем больше элементов допускается в списке решений, тем выше вероятность того, что он содержит верное решение, но при этом увеличивается время анализа и возрастает вероятность ошибки второго рода. Данные противоречия приводят к необходимости выбора оптимального набора значений порогов K и E для каждого из алгоритмов модуля распознавания.

Критериями эффективности модуля распознавания являются вероятности возможных исходов анализа изображения, а также время его анализа:

• -   P right — вероятность правильного распознавания

текстовой метки на изображении;

• -   P err - вероятность неправильного распознавания

текстовой метки на изображении;

• -    Pfalse — вероятность распознавания ложной метки на изображении, не содержащем ее образ;

• -    T - среднее время анализа изображения.

3.    Метод оптимизации процесса управления списками решений

Таким образом, задача настройки порогов АУС формулируется как задача параметрической оптимизации, где множество параметров состоит из param = { K L , E L , K S , E _S , K K , E _K , K R , E R } либо из некоторого подмножества param , а критериями эффективности анализа информативного изображения являются: P _right , P _err , P _false , T . Некоторый конкретный набор значений параметров АУС назовем конфигурацией АУС.

В работах [1,2] предложено производить спецификацию алгоритмов модуля распознавания с использованием массивов прецедентов - структурированной априорной информации о тестовой выборке изображений. Массив прецедентов включает информацию о координатах текстовой метки и отдельных ее символов, а также о классах символов по каждому тестовому изображению. Помимо возможности спецификации, он позволяет вычислять критерии эффективности модуля и его отдельных алгоритмов, что необходимо при проведении оптимизации модуля распознавания.

Если количество конфигураций невелико, то выбор оптимальной конфигурац ии сводится к вычис- лению критериев оптимальности каждой из них путем анализа выхода модуля по некоторой экзаменационной последовательности изображений. Однако часто на практике вычисление критериев оптимальности всех конфигураций неприемлемо из-за высоких вычислительных затрат ввиду большого количества конфигураций и (или) существенных затрат времени на вычисление критериев отдельной кон-фигурац ии.

Для сокращения вычислительных затрат на проведение параметрической оптимизации АУС предлагается след ующий метод. Он использует то, что параметры АУС являются порогами, определяющими количество элементов в списке решений - 0 или K . Это отличает параметры АУС от параметров прочих алгоритмов модуля. Особенность таких параметров-порогов заключается в том, что при задании им различных значений выход алгоритма-компонента изменяется не качеств енно (становится иным), а количественно - принимается некоторая часть списка решений согласно порогу, сам же список не изменяется. Это позволяет, зная полны й список решений алгоритма, определить результат при любых параметрах АУС, лишь единожды вычислив выход алгоритма по заданному изображению, что и позволяет значительно сократить вычислительные затраты.

Метод оптимизации АУС производ ит анализ изображений экзаменационной последовательности, статистич ески рассч итыв ая в ероя тно ст и исходов анализа изображений соотв етственно каждой конфигурации АУС . Опишем основные шаги метода:

• 1.    «Отключение» АУС.

• 2.    Цикл по изображениям экзаменационной последовательности и определение исхода ан ализа изображения при каждой конфигурации АУС.

  • 2.1.    Анализ экзаменационного изображения и получени е полного списка решений модуля распознавания.

• 2.2.    Анализ списка решений модуля распознавания.

Предварительно алгоритмы усечения списков решений «отключаются», т.е. их пороги устанавливаются в такие значения, при которых все списки решений пропускаются и не производится их усечение (либо производится до некоторого максимально допустимого размера). Поскольку АУС «отключены», то выходом модуля распознавания является полный список решений, сформированных по результатам анализа изображения.

Каждый код текстовой метки kod i из списка решений АФР { kod 1 , kod ₂,..., kod n } характеризуется набором признаков, которые определяют, в каких конфигурациях АУС данный вариант является решением.

Код kodi сформирован из совокупности элементов, каждый из которых характеризуется некоторой оценкой правдоподобия и местом в списке решений . Эти данные определяют значения порогов АУС, при которых решение может быть сформировано. Например, последовательность сегментов, составляющих решение, распознана на зоне, которая находится на третьем месте списка решений АЛ. Это значит, что при прочих равных условиях данная последовательность распознается при пороге на размер списка решений АЛ, большем либо равном трем: KL > 3 .

Помимо этого для каждой последовательности определяется, правильно ли сегменты распознаны и являются ли они образами символов, для чего используется массив прецедентов.

Полный список решений по каждому экзаменационному изображению анализируется след ующим образом: для каждой конфигураци и АУС устанавливается исход обработки изображения и инкрементируется переменн ая, соответствующая исход у.

Пусть списки решений возвращаются алгоритмами локализации, сегментации и формирования решений , а в качестве итогового решения принимается первый элемент списка АФР. Тогда каждый код текстовой метки обладает следующими характеристиками:

• -    решение получено посредством анализа зоны, занимающей позицию k _L списка решений АЛ ;

• -    список решений АЛ имеет оценку правдоподобия, равную e _L (оценка первого элемента списка);

• -    сегменты, из которых сформирован ответ, располагаются в пределах k s позиций списка решений АС;

• -    список решений АС имеет оценку правдоподобия, равную e _S (средняя оценка первых n элементов списка).

• 3.    Вычисление значений критериев оптимальности модуля распознавания.

• 4.    Модель зависимости времени анализа изображения от параметров алгоритмов усечения списков

При правильном распознавании текстовой метки в выходном массиве Right инкрементируются значения ячеек, соответствующих конфигурациям, при которых данное решение занимает первую позицию в списке: Right , j , k , m = Right, j , k , m + 1, где i e ^kL .. m , , j e 1.. e _L , k e k _S .. m _S , m e l.. e _S , m _L - максимально допустимое количество элементов в списке решений АЛ, m _S – максимально допустимое количество элементов в списке решений АС. Здесь предполагается, что оценки правдоподобия нормированы таким образом, что принимают значения из некоторого диапазона целых чисел от 1 до n _L и n _S , соответственно, для АЛ и АС. Размеры массива Right равны количеству соответствующих порогов – m L x n _L x m _S x n _S .

Для вычисления вероятностей ошибки распознавания и ложного распознавания аналогичным образом используются соответствующие массивы.

По результатам анализа экзаменационной последовательности изображений по каждой конфигура- ции АУС вычисляются значения Pright , Perr , Pfalse как доля соответствующих исходов от общего количества информативных и неинформативных экзаменационных изображений.

Объем памяти, необходимый для использования предложенного метода, зависит от количества кон-фигурац ий АУС. Исходя из этого, предъявляются соответствующие требования к аппаратному обеспечению компьютера, на котором проводятся вычисления по оптимизации АУС.

Приведем в качестве примера описанные выше алгоритмы системы распознавания идентификационных номеров железнодорожного транспорта. В процессе разработки алгоритмов были определены возможные значения порогов K _L , E _L , K _S , E _S , количество которых равно 5, 10, 80, 10 соответственно. При размерах массива 5 x 10 x 80 x 10 количество ячеек в таком массиве равно 40000, в памяти компьютера такой массив занимает менее 160Кб (при использовании типа integer), что не является ограничением для современных компьютеров. Тем не менее, перед использованием предложенного метода в прикладных задачах, которые могут обладать другими особенностями, след ует заранее учитывать объем памяти, необходимый для хранения соответствующей информации.

Таким образом, предложенный метод позволяет вычислить вероятностные критерии оптимальности каждой конфигурации АУС. Однако не менее значимым критерием является среднее время ан ализа изображения.

Среднее время T анализа изображения, поступающего на вход модуля распознавания, является значимым критерием оптимальности модуля. Оно определяет количество изображений, которое система распознавания «усп евает» анализировать за единицу времени .

В отличие от вероятностных критериев, время анализа изображения аппаратно зависимо. Достаточно сложно измерить его с высокой точностью. Как правило, системы распознавания создаются на платформе распространенных операционных систем Windows, что позволяет упростить разработку и снизить ее стоимость. Однако такие операционные системы не являются системами реального времени, что позволяет лишь приблизительно оценивать время выполнения функций тех или иных алгоритмов модуля.

Однако в большинстве случаев высокая точность не треб уется и достаточно лишь приблизительной оценки, поскольку время анализа изображения влияет на эффективность системы достаточно опосредованно и незначительные изменения времени мало сказываются на эффективности системы. Вследствие этого предлагается использовать сле- дующую модель, которая позволяет вычислять оценку T , учитывая лишь основные факторы, влияющие на время анализа.

Обозначим T _Z ^I – оценку среднего времени анализа информативной зоны и T _Z ^N – неинформативной. Сначала выч ислим T _Z ^I . Время анализа зоны определяется временем сегментации, распознавания сегментов и формирования форм. Сред нее время сегментации зоны T^S и время распознавания отдельного сег мен та T рассчитываются статистически.

Время распознавания всех сегментов зоны зависит главным образом от количества сегментов. Оно оценивается с учетом порога K S и распределения вероятности количества сегментов ( P ( C ^I ) для информативных зон и P ( C ^N ) для неинформативных), поскольку определенная доля зон содержит количество сегментов меньшее K _S , это след ует учитыв ать при оценке среднего времени распознавания сегментов зоны. Оценка времени распознавания сегментов зоны равна:

K s — 1                     m s

Trz(Ks, Y) = £ i • TK • P(CY) + £Ks • TK • P(CY), i-I                        i = KS где Y e {I, N} обозначает информативная или неинформативная зона.

Среднее время работы АФР пропорционально среднему количеств у решений, которое алгоритм формирует по зоне, в сумме с некоторым константным временем, которое затрачивает алгоритм, даже если ни одного решения не сформировано. Данная зависимость может быть установлена средствами вычислительной математики. В представленном далее примере она моделируется линейной ф ункци ей: Tf ( K_s , Y ) = c 1 • FCnt ( K_s , Y ) + c 2 .           Функция

FCnt ( K _S , Y ) рассчитывается статистически. Зависимость количества решений от порога на число сегментов может быть вычислена для каждой комбинации K _L и E _L , однако данные параметры оказывают, как правило, весьма косвенное влияние на функцию FCnt ( K _S , Y ) .

Найдем среднее время анализа i -ой зоны списка решений АЛ. Пусть среднее время сегментации равное T _S рассчитывается статистически. Среднее время распознавания сегментов зависит от вероятностей событий «зона информативна (неинформативна)» и «список решений АС принят». Первая вероятность определяется позицией i , она равна P ( L _i ) . Вероятность события «список решений АС принят» определяется порогом E _S и распределением вероятности оценки правдоподобия списка решений АС m S

P(LeY), она равна ^ P(Ej’ ). Отсюда среднее j = Ej время распознавания сегментов i -ой зоны вычисляется след ующим образом:

Trs ( i , K s , E j ) = P ( L i ) •

IP (ES-1)) • Trz ( Ks , I) + ( j=ES

+ (1 — P(Ll))-[ IP(Ej'N) |-Trz(Ks,N). Ij=eSJ

Среднее время формирования решений по i -ой зоне с учетом вероятностей указанных событий равно:

Tf (i,Ks) = P(Li) • f ^YlP(Ej,I) 1 • Tf (Kj,I) + I j=ESJ f ns

+ (1 — P ( L i )) •   ^ P ( E^S j- ^N ) • Tf ( K s , N ).

I j = ESJ

Таким образом, среднее время ан ализа i -ой зоны равно Tz ( i , K j , E s ) = T j + Trs ( i , K j , E s ) + Tf ( i , K s ), а среднее время анализа всего информативного изображения равно:

nL

Tii( K l , E l , K j , E j ) = T + ^ P ( E j , ¹ ) • ^ Tz (i , K j , E j ).

j=Eli

Аналогичным образом рассчитывается среднее время анализа неинформативного изображения:

nL

Tin ( K j , E j , K j , E j ) = T + ^ P ( E j’^N ) • ^ Tz ( i , K j , E j ).

j=Ej

Зная частоты появления информативного и неинформативного кадров p ^I и p ^N , найдем оценку среднего времени анализа произвольного кадра:

T^ = p¹ • Tii ( K j , E j , K j , E j ) + p ^N • Tin ( K j , E j , K j , E j ).

Предложенная модель учитывает лишь основные факторы, влияющие на среднее время анализа изображения, однако, как показывают дальнейшие эксперименты, позволяет достаточно точно оценить T .

5.    Практические эксперименты

Продемонстрируем применение предложенного метода оптимизации АУС на практике. Для проведения исследований были использованы алгоритмы оптоэлектронной системы идентификации объектов железнодорожного транспорта, описанные в п.1. Тестовая выборка состояла из 550 информативных изображений (видеокадров), содержащих образ железнодорожных вагонов с видимой текстовой меткой на борту. Для выборки предварительно был сформирован массив прецедентов. Тесты производились на компьютере со след ующей конфигурацией: частота двухъядерного микропроцессора 1,83 ГГц, объем оперативной памяти 1 Гб.

В качестве примера зависимости эффективности модуля от параметров АУС на рис. 5 представлены графики зависимостей вероятностных критериев оптимальности модуля распознавания Pright , Perr от порога KS = 1..50 при KL = 1 , ES = 1 , EL = 1 , KR = 1 , ER = 1 .

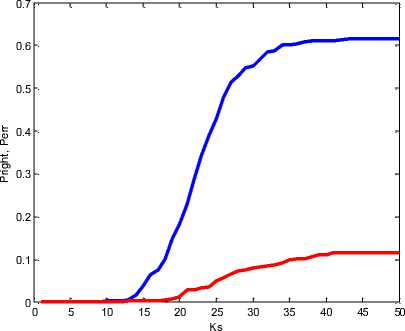
Рис. 5. Зависимость вероятностных критериев оптимальности модуля распознавания от порога на количество сегментов

След ует заметить, что вероятность распознавания идентификационного номера железнодорожного вагона на отдельно взятом кадре превышающая 0,6 является достаточно высоким показателем. При практическом использовании мод уля распознавания решение об идентификации объекта при нимает ся, как правило, по результатам ан ализа последовательности видеокадров, полученны х от нескольких видеоисточников (объект железнодорожного транспорта имеет четыре номера, нанесенные в разных местах). Поэтому вероятность идентификации объекта распознавания значительно выше.

На рис. 6 представлены графики зависимости среднего времени анализа отдельного информативного изображения (в среде MATLAB) от порога K _S = 20..45 при тех же параметрах.

средственно измеренное в процессе анализа мод улем изображений тестовой выборки.

Замеры времени производились в среде MATLAB, которая является интерпретатором, и в операционной среде Windows XP, которая не является операционной системой реального времени. В силу этих факторов результаты измерений T также являются лишь приблизительной оценкой. Тем не менее, как показывает рисунок 4, предложенный метод позволяет получить оценку T , достаточно близкую к результатам непосредственных измерений, что говорит о возможности использования предложенного метода оценки T в процессе параметрической оптимизации АУС.

Оптимизируем параметры: K _L , E _L , K _S , E _S алгоритмов, описанных в п.1. Применение предложенного метода дало следующие результаты . На рис. 7 представлено множество точек, соответствующих конфигурациям АУС. Координатами точек являются значения критериев оптимальности конфигураций: P right и оценка времени T .

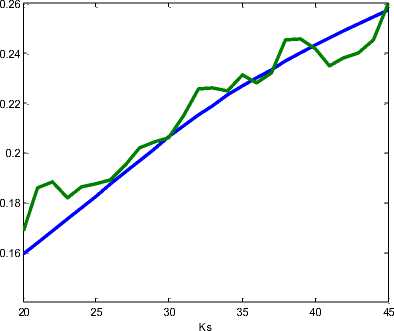
Рис. 6. Зависимость среднего времени анализа изображения от порога на количество сегментов

Гладкий график характеризует оценку T , вычисленную с использованием предложенной выше модели, второй график отображает время T , непо-

Из рисунк а видно, что точки образуют характерные фигуры, которые отражают рост вычислительных затрат по мере увеличения длины списка решений АС и прекращение по достижению некоторого значения K s роста вероятности правильного распознавания образа текстовой метки.

Руководствуясь целью максимизации P right , примем в качестве итоговой следующую конфигурацию АУС: K^{L =} 2, E^{L =} 1, K^{S =} 43, E^{S =} 2. Эта конфигурация P = 0,53 обеспечивает показатели эффективности: ^right , Pen- = ^0,07 , f^feis e 0 , T = 0,33. Затраты времени на вычисление критериев оптимальности всех конфигураций АУС, составления множества оптимальных по Парето конфигураций и выбора конечной конфигурации составили 20 минут 40 секунд.

Оценим время, затрачиваемое на получение того же самого множества критериев оптимальности каж-

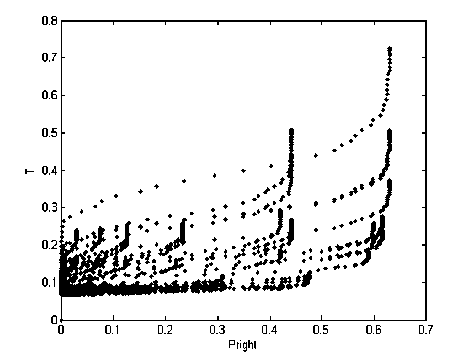
Рис. 7. Критерии оптимальности Pright , Perr и T множества конфигураций АУС дой конфигурации, если непосредственно вычислять эффективность каждой конфигурации. Количество конфигураций равно 3x10x80x10=24000. Примем время вычисления эффективности отдельной конфигурации равным времени вычисления эффективности конфигурации {KL = 1, EL = 1, KS = 20, ES = 1}, которой соответствует небольшой объем вычислений по сравнению с большинством прочих конфигураций (значительно ниже среднего). Это время равно 67 секундам, отсюда следует, что для непосредственного вычисления критериев оптимальности всех конфигураций потребуется более чем 67x24000=1608000 секунд (18 суток). Данный пример наглядно показывает, что применение предлагаемого метода позволяет производить параметрическую оптимизацию АУС модуля распознавания в тех задачах, где применение непосредственного вычисления критериев оптимальности модуля сопряжено с неприемлемыми затратами времени.

Заключение

Системы распознавания текстовых меток на видеоизображениях находят все более широкое практическое применение. Их основным компонентом является программное обеспечение, реализующее алгоритмы локализации, сегментации, распознавания и принятия решений. С целью повышения эффективности алгоритмического обеспечения таких систем в работах [1,2] предложено межд у промежуточными этапами передавать списки возможных вариантов решений, что дает возможность не потерять на промежуточных этапах истин ное решение. Чем больше список, тем выше вероятность того, что он содержит верное решение, но при этом растет время анализа и увеличивается вероятность ошибки. Данные противоречия приводят к необходимости выбора оптимального набора параметров (конфигурации) алгоритмов усечения списков, т.е. ставят задач у параметрической оптимизации этих алгоритмов.

Обычно на практике вычисление критериев оптимальности всех конфигураций неприемлемо из-за высоких вычислительных затрат.

Для решения этой проблемы в статье предложен метод оптимизации параметров алгоритмов усечения списков, треб ующий невысоких вычислительных затрат.

Метод использует тот факт, что параметры АУС являются порогами, определяющими количество элементов в списке решений . Особенность таких параметров-порогов заключается в том, что полный список решений алгоритма позволяет определить результат при любых параметрах АУС, запустив алгоритм единожды, чтобы рассчитать этот список. Это свойство отличает параметры АУС от обычных параметров алгоритмов.

Экспериментальные исследования по оптимизации системы распознавания идентификационных номеров железнодорожного транспорта подтвердили эффективность предлагаемого метода.