Метод парных расстоянии в задаче полетной юстировки астродатчиков системы ориентации космических аппаратов
Автор: Суховилов Борис Максович
Статья в выпуске: 23 (95), 2007 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/147154594
IDR: 147154594 | УДК: 629.78.018:621.397.13
Текст статьи Метод парных расстоянии в задаче полетной юстировки астродатчиков системы ориентации космических аппаратов
По мере улучшения точности и надежности астрономических датчиков (АД) систем ориентации (СО) космических аппаратов (КА) доля погрешностей юстировочных параметров СО в общей погрешности ориентации КА возрастает [1]. Так, в работе [2] показано, что точность ориентации КА, оснащенных СО на базе двух и более АД, существенно зависит от точности предполетной юстировки взаимного положения АД. Отметим также, что точность оценки взаимного положения приборных систем координат (ПСК) АД непосредственно влияет на качество работы бортового алгоритма идентификации звезд, основанного на сравнении угловых расстояний между звездами.
В то же время следует отметить, что даже идеальная предполетная юстировка взаимного положения АД не способна устранить погрешности, возникающие во время эксплуатации КА. Их причинами являются: вибрационные и ударные нагрузки в моменты запуска и отделения КА; циклические температурные изменения в процессе полета; деформации оснований и деталей датчиков, вызванные старением и воздействием космической среды. Эти факторы становятся особенно ощутимыми, если КА имеет значительный срок активного существования.
Одним из эффективных методов компенсации влияния указанных факторов на точность ориентации КА является полетная юстировка взаимного положения ПСК АД, базирующаяся на методе парных расстояний, основанном на сравнении угловых расстояний между звездами, одновременно визируемыми АД, с эталонными расстояниями между этими же звездами, взятыми из бортового звездного каталога. Несомненным преимуществом метода является его применимость в условиях, когда каждый АД визирует только одну звезду.
Прежде, чем мы применим метод парных расстояний к задаче полетной юстировки, необходимо получить статистическую модель измерений АД направления на звезду.
-
1. Статистическая модель измерений астродатчика КА
В связи с повышением требований к точности ориентации КА происходит непрерывное совершенствование и улучшение точностных характеристик датчиков ориентации. Особое место занимают астродатчики, обеспечивающие в настоящее время наивысшую точность. Астродатчики по способу их взаимного расположения относительно корпуса КА делятся на два класса: астроследящие устройства и астровизирующие устройства. Астроследящие уст ройства представляют собой астродатчик, смонтированный в кардановом подвесе, обеспечивающем совместно с электромеханическими приводами слежение за выбранными астроориентирами. Под астровизирующим устройством понимается автоматическая система с жестко закрепленным на корпусе КА звездным датчиком, с помощью которого определяются направления на визируемые звезды.
Широкое применение АД в практике потребовало создания и анализа моделей погрешностей измерения АД. Поскольку погрешности АД во многом носят случайный характер, актуальной является задача разработки статистической модели погрешностей АД.
-
1.1. Статистическая модель астроследящей системы на основе оптического датчика
в кардановом подвесе
В настоящем параграфе представлена статистическая модель погрешностей измерения АД, астроследящее устройство которого имеет две степени свободы (установлено в двухстепенном кардановом подвесе). В дальнейшем будет показано, что данная модель распространяется также на АД астровизирующего типа, жестко прикрепленного к корпусу КА. Модель учитывает как приборные погрешности АД так и неточности выставки приборных систем координат АД в связанной системе координат (ССК) КА и представляет собой ковариационную матрицу погрешностей измерения направляющего косинуса на звезду в ССК КА.
Введем следующие обозначения. Пусть ОА - истинный, а ОА - измеренный направляющий косинус на звезду в ПСК OXYZ АД. Вектор ОА составляет угол у с плоскостью XOY, а отрезок ОЕ (проекция ОА на плоскость XOY) с осью ОХ составляет угол а (см. рис. 1). Обозначим через Ц] = AD - вектор погрешности измерения направления на звезду в плоскости Р, перпендикулярной оси OZ, и проходящей через точку А, накрываемую кругом с радиусом АВ = cosy, q2= ^ ~ вектор погрешности измерения направления на звезду в плоскости ОВАЕ. Поскольку векторы ^ и ц2 перпендикулярны, значение модуля [т|| вектора суммарной погрешности измерения направляющего косинуса на звезду составит |т|| = +|q2| -
С учетом того, что вектор ОА перпендикулярен векторам ц, и ц2, получаем, что вектор ОА также перпендикулярен вектору суммарной погрешности q. Определим значения (qj и |q2| в следующем виде:
IqJ = А^ + Aacosy;
|q21 = А^2 + Аб, где А^, А^2 - погрешности наведения на звезду вектора ОА соответственно в плоскостях Р и ОВАЕ; Аа, АЬ - погрешности отсчетных устройств АД соответственно по углам а и у в плоскостях Р и ОВАЕ.
Полагая погрешности А^, А^, Аа, АЬ , случайными и независимыми, получаем среднеквадратическое отклонение (СКО) ст^ и о^ модулей векторов погрешностей jqj и ]т>2| в виде:
% +aucos г;
/ 2 2
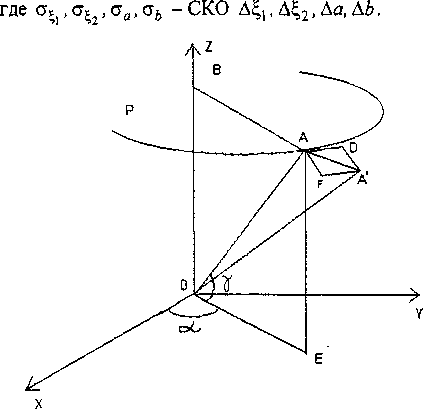
Рис. 1. Схема формирования погрешностей измерений АД
Используя (1), определим ковариационную матрицу вектора q. Обозначим 0 - истинный, совпадающий с вектором ОА, направляющий косинус звезды в ПСК, 0 - измеренный, совпадающий с вектором ОА , направляющий косинус звезды в ПСК АД. Значение вектора q погрешности измерения направляющего косинуса на звезду в ПСК АД составит:
п = Р-Р
В соответствии с рис. 1, выразим декартовые координаты вектора q через его составляющие q.
и q2 в следующем виде:
-sin a
q =
cos a
sin у cos a sinysina -cosy
^J 1*12
Поскольку векторы q] и q2 независимы, кова риационная матрица М qqT вектора q составит:
M[qqT^ = Q
О
Используя значение вектора
Р = [Р] р2 Рз ] т= [cos у cos a cos у sin a преобразуем (2) к виду (4):
M^qq1^ = siny]T,(3)
2 • 2 sin a +
2 2
+аЛз cos a
/2 2 \ • ^
[% -°njsm2a
-a^) sin 2a
2 • 2
sin a +
2 2
+o^ cos a
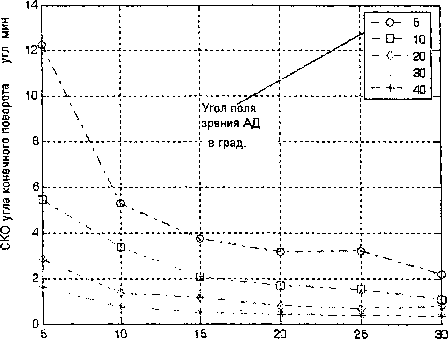
- Формула (4) представляет статистическую модель астроследящего устройства в виде ковариационной матрицы вектора q - погрешности измерения направления на звезду. 1.2. Статистическая модель астровизирующей системы, жестко закрепленной на корпусе КА Используем полученные в предыдущем параграфе результаты для вывода статистической модели астровизирующего датчика, жестко закрепленного на корпусе КА. Для этого оценим значения оЛ1 и а^, делая обоснованные для практики допущения о^ = ст^ =5] и оа = аь = 32. В общем случае ст^ * аЧ2, так как значение ач зависит от угла у . При измерении угла у в диапазоне паспортных значений от -5° до 85° значение о2 изменяется от 62 до 52 +52, в то время как значение сг^ постоянно и равно 52 + 32. Поэтому для получения гарантированной оценки точности АД примем для аЛ[ и о^ одинаковое наибольшее возможное значение, равное a = 7sf +82 . С учетом того, что ст^ = а22 = ст2/2, где а -СКО погрешности измерения направления на звезду, значение ковариационной матрицы вектора q примет следующий вид: Используя значение вектора 0 из (3), преобразуем (5) к следующему компактному виду: M[qqT] = 1 - cos2 a cos2 у -sin а cos а cos2 у cos у sin у cos а -sin а cos а cos2 у 1 — cos2 у sin2 а -cosу sin у sin а -sin у cos у cos а -sin у cos у 1 — sin2 у M[qqT] = = —(I3x3-PPT), (6) 1-р? ""РА -Р1Рз ~Р1Р2 1-Р2 ~Р2Рз ~Р1Рз ~Р2Рз 1-Рз где 13х3 - единичная матрица размером 3x3 . Формула (6) определяет ковариационную матрицу вектора q, позволяющую гарантированно оценивать точность измерения направления на звезду в ПСК АД. Причем, формула (6) является справедливой и для астровизирующего устройства с широкоугольным АД (например, на базе ПЗС матрицы), жестко закрепленном на корпусе КА, показания которого снимаются не с отчетных механических устройств карданного подвеса, а с чувствительного слоя ПЗС матрицы, так как в ней исключены все особенности конкретного типа АД. 1.3. Обобщенная статистическая модель астродатчика КА В дополнение к измерительным погрешностям АД учтем в модели (6) погрешность направляющего косинуса на звезду в ССК аппарата, возникающую из-за неточности знания положения ПСК в ССК КА. Пусть Со - истинная матрица перехода из ПСК в ССК, а С - оценочное значение матрицы Со. При этом, учитывая малость отклонения С от Со, матрицу С представим в виде: С = (I3x3 + D)C0, О d3 где D= -d3 О d2 ~dx ~d2 dx 0 - кососимметричная мат рица погрешностей dx,d3, d3 ПСК АД в ССК КА. Значение истинного вектора Рс направляющего косинуса на звезду в ССК КА и его измеренное значение Рс составят: Рс=С0Р; Л=(1зх3+О)С0₽. Вектор погрешности измерения направляющего косинуса на звезду в ССК Др = рс - рсс точностью до малых второго порядка будет равен: Ap = (l3x3+D)C0p-C0p=C0q + PD, где D = [dx d3 d3] ; Рс=с0Р = [Рс1 Рс2 Рс3]т; о Рс3 Р= -Рез О Рс2 —Pel ~Рс2 Pci О С учетом независимости векторов q и D ковариационная матрица вектора др составит: М [ дрД рт ] = С0М [qqT ] Cj + РМ [55т ] Рт, (7) где m[dDt] - ковариационная матрица вектора D. Проведя подстановку в (7) значения матрицы Р, ковариационной матрицы M[qqT] из формулы (6) и принимая в качестве дисперсий погрешностей dx,dI, d3 величину d2, равную d2 =шах|м^2], М^.М^2]} получаем значение ковариационной матрицы м[дрдрт] в следующем виде: м[дрдрт] = = С0о72(13х3-ррт)С?+^РРт = = (o72 + rf2)(l3x3-pcpj). (8) Таким образом, формула (8), определяющая значение ковариационной матрицы погрешностей измерения направляющего косинуса на звезду в ССК КА и учитывающая как погрешности АД, так и неточности установки ПСК АД в ССК КА, представляет искомую обобщенную статистическую модель погрешностей АД, позволяющую гарантированно оценивать погрешности измерения направления на звезды в ССК КА. 2. Математическая модель метода парных расстояний в задаче полетной юстировки астродатчиков системы ориентации космических аппаратов В основе рассматриваемого метода оценки взаимного положения ПСК АД лежит метод парных расстояний, базирующийся на сравнении угловых расстояний между звездами, одновременно визируемыми АД, с эталонными расстояниями между этими же звездами, взятыми из бортового звездного каталога. При этом достаточно, чтобы каждый АД, в процессе определения ориентации КА измерял координаты только одной звезды. В качестве оцениваемого юстировочного параметра рассматривается матрица вращения А, определяющая взаимное положение ПСК АД. Отметим, что в качестве оцениваемого юстировочного параметра, можно также рассматривать матрицу вращения, определяющую взаимное положение систем координат АД, связанных с корпусом КА, по- скольку в предыдущем параграфе получены статистические модели АД, как для первого случая -формула (6), так и для второго случая - формула (8). Выбор юстировочного параметра определяется необходимостью повышения эффективности решения конкретной задачи. Например, для повышения надежности работы бортового алгоритма идентификации звезд, в качестве юстировочного параметра необходимо выбрать матрицу вращения А, определяющую взаимное положение ПСК АД. Матрица вращения А связана с косинусом С* угла между двумя звездами, определяемого по результатам измерений двух АД, с точностью до погрешностей измерения следующим соотношением: «^«С*, (9) где а,, р, - векторы направляющих косинусов звезд, измеренные первым и вторым АД; i, N -соответственно, порядковый номер и количество парных измерений звезд. Векторы направляющих косинусов звезд с учетом погрешностей измерения составят: а, = а, + Да ' (10) ₽; =Р, +д^, где а,,р, - истинные направляющие косинусы звезд; Да,, Др, - векторы нормально распределенных погрешностей измерения направлений на звезды. Ковариационные матрицы векторов Да, и ДР, в соответствии с (6) составят: Г 2 , . (П) м[др,дрт] = -^(13х3-р,.рт), где ор а2 - СКО погрешности измерения направления на звезду, соответственно для первого и второго АД. Учитывая, что погрешность ДС, определения косинуса угла между парой звезд равна: ДС, = С,-а^ Ар,, (12) где С, - косинус угла между визируемыми звездами, рассчитанный по данным бортового звездного каталога, подставляя (10) в (12) и пренебрегая величинами второго порядка малости, получаем погрешность косинуса угла АС, в виде: ДС, =Аа^Ар,+а^ААр( (13) Из (13) следует, что погрешность ДС, имеет нормальный закон распределения, как сумма проекций нормально распределенных векторов Аа, и АР,, умноженных на неслучайные коэффициенты, а математическое ожидание ДС, равно нулю. м[да,Да^ ] = -у Дисперсия Д величины ДС,, вычисленная с учетом независимости векторов Да,, др, с использованием формул (11) и (13), составит: Д =м[дс,2] = |(ст12+^)(1-С^ (14) Важно отметить, что полученное значение дисперсии в формуле (14) позволяет правильно взвешивать измерения, проводимые с помощью комбинирования пар различных оптикоэлектронных, радио и других приборов, имеющих разную приборную точность измерения направления на источники излучения и разные углы между последовательно визируемыми источниками в каждом акте измерения. Это открывает возможность полетной юстировки с использованием метода парных расстояний между ПСК различных датчиков (не только АД), умеющих измерять направление на некоторый источник энергии, например, юстировать взаимное положение датчиков Солнца, Земли и т.п. Используя полученные результаты, оценим матрицу А на основе метода максимального правдоподобия, вычислительной схемой которого в данном случае является минимизация функционала: N 1 2 F = ^—(Д-a^Ap,) —^min. (15) Представим матрицу А через углы Крылова Ф, 9, \|/ в следующем виде: Пусть ф0, 90, v0 - углы Крылова, установленные на этапе предполетной подготовки, определяющие известную матрицу Ао начальной вза имной ориентации ПСК АД. Принимая во внимание, что погрешности взаимной ориентации ПСК АД, выраженные в углах Крылова, не превышают одного градуса, для минимизации функционала (15) применим схему Гаусса, заключающуюся в составлении фундаментальной системы уравнений на основе линеаризации матрицы А в точке текущего приближения ф0,90,у0 и применении по следовательных итераций для оценки углов Крылова ф, 9, ф по формулам: Фу+) =ФУ+Л<Р/ .9V+1=9,+A9;; Vy+i =Vy +Ауу, где у - номер итерации. Представляя поправки Аф7, А0;, Дф7 в форме вектора А7 = |^Лф7 А0у Дф7 ]Т, получаем решение для вектора Ау в виде: А где bJk-1z В - dA j T dA, T dA. a, —^p, + a,T —^p, + a,T —^p, 1 dtp 1 1 de 1 1 dtp и T dA, T dA, T dA, a2 "T"P2 +a2 "477^2 +a2 "T~₽2 d^ d^ dx^ т dA т dA т dA. + aN-^r^N+aN”r~PN dtp dti dtp - матрица размера ^xЗ коэффициентов линеаризованной фундаментальной системы нау-й итерации, К4 = Д/д 0 0 ■ 1/^2 ■ ■ 0 " • 0 0 0 ■ - диагональная матрица весов, размером NxN; Z7=[z, z2 z3...z^]T - вектор с компонентами z, = a/ АуР, - С,; А7 - значение матрицы А на j-й итерации. Точность получаемого решения оценивается Кд - ковариационной матрицей оценки вектора углов Крылова ф, 6, у, вычисляемой по формуле: Кд =м[аАт] = (втК"1в)4, (18) где В - матрица коэффициентов линеаризованной фундаментальной системы, определенная в (17), в конце итерационного процесса. Представим А, - истинную матрицу взаимной ориентации ПСК АД - в виде: А,=(13х3+Е)А, (19) где А - оценка матрицы А,, вычисленная в конце итерационного процесса по формуле (16), 0 6е3 -6s2 Е = -6е3 0 бЕ] - матрица поправок. -5е2 —5б] 0 Пусть вектор бе = [58] бе2 5е3]т составлен из поправок 6е1,5е2, 583. Примем в качестве интегральной характеристики точности взаимного положения АД - СКО погрешности оценки угла конечного поворота 5 между ПСК первого и второго АД: 6 = VSp(K£), (20) где Sp(K£) - следковариационной матрицы К£ вектора 5s. Значение ковариационной матрицы КЕ может быть получено из матрицы Кд путем сравнения матрицы погрешностей оценки взаимной ориентации, выраженной через матрицу поправок Е: 6А = ЕА (21) с матрицей погрешностей оценки взаимной ориентации, выраженной через производные по углам Крылова: 5А = ^^5Ф/, (22) где для углов ф, 6, у приняты обозначе ния: ф] = ф, ф2 = 6, ф3 = ф . Сравнивая матрицы 6А из выражений (21), (22) поэлементно и решая полученное уравнение относительно вектора 5 s, получаем [3, с. 72]: 5Ё = Н"1(ф], ф2, ф3)5ф, (23) где вектор 5ф = [5ф] 5ф2 5ф3]т, а элементы мат рицы Н-1(ф], ф2, ф3) вычисляются по формуле , -1 1 [ 8Ак Д = ~/ --~х Аг. 7 2^ 5ф7к где Ак - к-й столбец матрицы А, х - знак век торного произведения. Для принятого порядка поворотов, определяющих матрицу взаимной ориентации ПСК АД в виде (16), значение матрицы И1вычисляется по следующей формуле: Н1 1 0 -sin 9 0 СО8ф 8ШфСО80 0 8П1ф СО8фСО80 С учетом (23) и (24) ковариационная матрица К£составит: К£=НчКд(Н-1)т. Проверка полученного решения осуществлялась методом статистических испытаний на ЭВМ. В процессе испытаний оценивались углы Крылова, определяющие матрицу взаимной ориентации ПСК двух АД. В качестве обобщенного критерия оценки матрицы взаимной ориентации ПСК АД использовалось СКО погрешности оценки 5 угла конечного поворота между ПСК первого и второго АД, при следующих, наиболее часто применяемых на практике, условиях: оптические оси АД расположены под углом 90°, угол поля зрения АД составляет 5°, 10°, 20°, 30°, 40°; СКО погрешностей измерения направления на звезду первого и второго АД соответствовали 5, = 62 = 10"; количество парных измерений направлений на звезды равнялось 5, 10, 15, 20, 25, 30. Начальная неточность взаимной установки ПСК АД по каждому углу Крылова составляла 1°. Для каждой комбинации угла поля зрения АД и количества парных измере- ний направлений на звезды генерировались 50 случайных, распределенных по равномерному закону внутри поля зрения АД, пар тестовых положений звезд с последующим вычислением усредненного значения 5. На рис. 2 приведены графики усредненных значений СКО погрешности оценки угла конечного поворота 5 по всем реализациям в зависимости от угла поля зрения и количества парных измерений направлений на звезды. Приведенные данные статистических испытаний показывают, что для указанных диапазонов изменения угла поля зрения АД и количества парных измерений звезд, при прочих равных условиях, увеличение количества парных измерений звезд в 6 раз примерно во столько же раз увеличивает точность оценки угла конечного поворота между ПСК АД. Существенное влияние на точность определения взаимной ориентации ПСК АД оказывает величина угла поля зрения АД, с уменьшением которой критерий д возрастает примерно в обратно пропорциональной зависимости по отношению к изменению величины угла поля зрения АД. Количество парных измерений направлений на звезды Рис. 2. Влияние количества парных измерении звезд и угла поля зрения АД на СКО погрешности оценки угла конечного поворота между ПСК АД Как было отмечено ранее, полученные результаты полетной юстировки взаимного положения ПСК АД необходимы для качественной работы бортового алгоритма идентификации звезд, основанного на сравнении угловых расстояний между визируемыми звездами с эталонными данными из бортового звездного каталога. При этом важна точность определения значения косинуса угла между визируемыми звездами С* в соответствии с формулой (9). Основываясь на полученных результатах, оценим влияние результатов полетной юстировки АД на точность определения С*. Погрешность А, измерения С* с точностью до малых величин второго порядка равна Sj = ди + ^2/ > где Аи - составляющая погрешности, зависящая от погрешностей измерения астродатчиками направлений на пару звезд, с дисперсией а2(Лп) = |Н+ст2)(1-С,2)> где А2, - составляющая погрешности, зависящая от точности оценки матрицы А, равная А2; = (а, х Ар, )Т Зе , с дисперсией, определяемой по формуле: о2(Д2, ) = (а, хАР, )ТК£(а; хАр, ). (25) Выражение (25) представляет квадратичную форму относительно единичного вектора а, х АР;, для которой справедливо неравенство 8р(К£) = ^Х,>Хти>(а,хАр,)Тх ,=1 xK£(a,xAp, )>Xmm >0, где Л, - собственные значения матрицы ковариации К г i - наименьшее и наибольшее собственные значения матрицы К£. Так как Sp(K£) = §2,с учетом (25) получаем а2 (А2,) < 82. Поскольку значение о(А1г ) на порядок меньше о(А2, ), для принятых условий (ст, = с2 = 10", С, « 0), то значение СКО погрешности оценки косинуса угла между визируемыми звездами as подчиняется следующему ограничению: С учетом выражения (26) и значений СКО погрешности оценки 8 угла конечного поворота между ПСК АД, взятых из рис. 2 при А = 5 и N= 30, следует, что полетная юстировка по 30 парным измерениям звезд в среднем от 3 до 6 раз уменьшает погрешность измерения угловых расстояний между звездами в рассматриваемом диапазоне углов поля зрения АД. Тем самым повышается надежность работы бортового алгоритма идентификации звезд, использующего в качестве классификационных признаков идентификации угловые расстояния между звездами. Также отметим, что был рассмотрен еще один итерационный алгоритм оценки матрицы взаимной ориентации между ПСК АД, при параметризации матрицы взаимной ориентации в соответствии с формулой А = (13х3+Е)А0, где Ао - известная матрица начальной взаимной ориентации, обеспечиваемая на этапе предполетной юстировки, Е - матрица поправок, как представлено в (19). В этом случае итерационная процедура осуществлялась для вектора поправок Зв, вычисляемого по формуле (17) с матрицей В, строки которой составлены из векторных произведений а, х Ао р,. При этом ковариационная матрица К£ вектора 5ё непосредственно вычислялась из формулы (18), а интегральная характеристика точности оценки взаимного положения АД - СКО погрешности угла конечного поворота между ПСК АД по формуле (20). Исследования рассматриваемого алгоритма показали, что при вычислении оценки матрицы взаимной ориентации между ПСК АД необходимо осуществлять процедуру ее ортогонализации на каждом шаге итерационного процесса. Выполнение ортогонализации матрицы достаточно трудоемкая с вычислительной точки зрения операция, состоящая в поиске ортогональной матрицы V, ближайшей к вычисленной на очередной итерации матрице А. Известно [4, с. 317], что если матрица А не особенная, то она представима в виде: A = SV, (27) где S = (AAT)^2 - симметричная матрица, а V -ближайшая ортогональная матрица. Подставляя в (27) значение матрицы S, получаем формулу для вычисления ближайшей ортогональной матрицы в виде: V = (AATrV2A. (28) Процедура вычисления ближайшей ортогональной матрицы по формуле (28) трудоемка с вычислительной точки зрения, так как требует нахождения корня из матрицы. В данном случае эта трудоемкость непосредственно влияет на производительность работы алгоритма, так как ортогонализация выполняется многократно в течение итерационного процесса. С другой стороны, как показали численные эксперименты, в процессе итераций, допустимо иметь матрицу А, ортогональную с точностью до малых второго порядка. Поэтому предлагается использовать следующий алгоритм ортогонализации. Матрица А близка к ортогональной и для вычисления (ААТ)~1/2 может быть предложен более простой с вычислительной точки зрения способ, чем извлечение корня из матрицы. Способ основан на том, что (ААТ) «13х3 и матричная функция (АА1)-^2 может быть с достаточно высокой степенью точности представлена рядом Тейлора для функции у = Г^2 : хч/2 =1-1(%-1) + |(х-1)2+...(29) Подставляя ААТ в (29) вместо переменной х и 13х3 вместо 1, получим: (ААт)^2=13х3-0,5(ААт-13х3).(30) Подставив (30) в (28), получим ближайшую ортогональную матрицу в виде: V = 1,5А-0,5ААтА .(31) Искомая матрица V, определенная (31), ортогональна с точностью до малых 2-го порядка, что в итоге и требовалось получить. Что касается сравнения двух рассматриваемых алгоритмов оценки матрицы взаимной ориентации между ПСК АД, необходимо отметить более простую вычислительную схему алгоритма, оценивающего вектор поправок матрицы взаимной ориентации. Этот алгоритм не использует тригонометрических функций, в отличие от алгоритма оценки углов Крылова. Вычислительная точность обоих алгоритмов, как показали расчеты, одинакова, и все сделанные выше выводы по итогам статистических испытаний на ЭВМ справедливы и при использовании второго алгоритма определения матрицы взаимной ориентации между ПСК АД.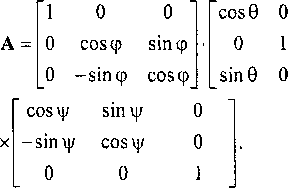
Список литературы Метод парных расстоянии в задаче полетной юстировки астродатчиков системы ориентации космических аппаратов
- Bowers, E. J., Jr. Calibration of star-tracker bias errors on ОАО/E. J. Bowers, Jr.//Proc. National Aerospace Electronics Conf., Dayton, Ohio, 1967.-P. 99-104.
- Real time spacecraft attitude determination by star pattern recognition -Further results/Т. Е. Strikwerda et al.//17th Aerospace sciences meeting, New Orleans, LA., 15-17 Jan. 1979. 3.
- Shuster, M. D. Tree-Axis Attitude Determination from Vector Observations/M. D. Shuster,S. D. Oh//Journal of Guidance and Control. -Vol. 4, №1.-1981.-P. 70-77. 4.
- Гантмахер, Ф. Р. Теория матриц/Ф. Р. Гантмахер. -M.: Наука. -1966. -576 с.


