Метод подавления импульсных помех при обработке сигналов и изображений c использованием нелинейных фазовых фильтров

Импульсные помехи (ИП) являются одним из основных факторов, ухудшающих качество изображений, и могут возникать как при передаче сигналов, несущих информацию об изображениях, по каналам связи ( в особенности коммутируемым проводным каналам низкого качества и радиоканалам), так и непосредственно в процессе их обработки (например, вследствие ошибок декодирования) [1 - 3]. Если ИП носят точечный характер, их влияние удается сравнительно просто свести к минимуму путем "исправления" пораженных помехой элементов изображения с помощью интерполяции по соседним элементам [1] или медианной фильтрации [3]. При обработке одномерных сигналов на практике широко используется ограничение, бланкирование и другие подобные нелинейные операции подавления ИП [4]. Однако все эти методы становятся малоэффективными, если помеха поражает не один, а достаточно много соседних элементов, т.е. становится соизмеримой по размерам с изображением (или по длительности - с сигналом).

Для подавления таких видов ИП в принципе можно использовать методы нелинейной фильтрации по минимуму среднего квадрата отклонения (СКО), основанные на представлении сигналов и изображений марковскими моделями в пространстве состояний [5,6]. Но возможности их практической реализации весьма ограничены - как из-за отсутствия точных решений у соответствующих уравнений для апостериорных распределений и необходимости использования многочисленных и не всегда оправданных приближений, так и потому, что вопрос о применимости марковских моделей для изображений часто остается открытым [6]. Кроме того, критерий минимума СКО далеко не всегда приемлем для оценки качества изображений и других видов непрерывных сообщений, особенно, если речь идет о субъективном восприятии.

В то же время значительный прогресс, достигнутый за последние годы в технике цифровой обработки сигналов, появление процессоров и других видов СБИС с высоким быстродействием значительно расширяют возможности реализации более сложных алгоритмов обработки, чем перечисленные выше простейшие нелинейные преобразования. Один из таких алгоритмов предложен авторами в [7] и включает в себя такие операции, которые позволяют сжать импульсы помехи до точечных практически без изменения полезного сигнала, что дает возможность затем подавить их одним из известных указанных выше методов. Цель данной работы - его обобщение на двумерные сигналы (изображения и поля).

1. МОДЕЛИ ИМПУЛЬСНЫХ ПОМЕХ

Импульсные помехи в каналах связи и на изображениях отличаются от других видов шумов тем, что имеют значительно меньшую длительность или размеры по сравнению с анализируемой областью одномерного или двумерного сигнала [1,8]. Как правило, их можно рассматривать как квазидетерминированные функции времени или пространственных координат, форма которых известна, а случайными являются только параметры. В зависимости от вида сигнала (модулированный сигнал в канале связи, комплексная амплитуда волнового поля, яркость точки двумерного изображения и т.п.) ИП может принимать значения на множествах комплексных, вещественных или положительных чисел. Используя, как наиболее общее, комплексное представление, можно записать выражение для ИП в виде u (ti, t 2 ) = Е Ak х k                                                 (1)

^х q ( t i ^- t i k , t 2 ^- t 2 k ; ^T i k , ^T 2 k ) exp ( W k )

где q (t1, 12; T1, T2) - детерминированная функция , описывающая форму огибающей ИП, Ak, 11k, 12k, T1k, T2k, фк - случайные параметры, имеющие смысл амплитуды, координат, размеров и фазы k-го импульса. Как правило, их можно считать независимыми с известными плотностями вероятностей. В рассматриваемых здесь задачах свойства последовательностей ИП в целом не существенны и алгоритмы фильтрации синтезируются с учетом характеристик отдельных импульсов. При этом начало координат можно связать с центром анализируемого импульса, так что модель одиночной ИП принимает вид u (t, 0) = Aq (t, т) exp (ю),                (2)

где t = ( t 1 , 1 2 ) e T - вектор координат из некоторой двумерной области Т , T n = ( T 1 , т 2 ) и 0 = ( A , т 1 , т 2 , ф ) - векторы случайных параметров. В качестве простого приближения для формы ИП на изображениях можно использовать гауссовскую функцию

Г      22

I       12

q (t, т) = exp j--1y - -^y [ .

^ 2 т 1     2 т 2 J

В каналах связи ИП обычно имеют осцилляции [8], для учета которых можно использовать модель вида

I k ^t^ |     nt q (t, Tn ) = expl--I sin—,               (4)

• V     ^T n J       ^T n

  где t - одномерная временная координата, к _ф - коэффициент формы, характеризующий затухание ИП. При k _ф >>0 ИП практически не имеет осцилляций, а при k _ф = 0 осцилляции принимают вид незатухающего гармонического колебания. Результаты статистического анализа реальных радиопомех [6,8] показывают, что для их амплитуд типично логнормальное распределение

  
  

  Критерием оптимальности блоков нелинейной селекции и фильтра в целом при обработке временных сигналов обычно является минимум СКО

  ^{е 2} = ( z о ^- z o ( 2 , ⁽⁹⁾

  
  

  w ( A ) =

  
  

  А &4 2 Л

  
  

  exp

  
  

  ln² ( A / ц ) )

  2 ^  J ’

  
  
  
  

  где о , ц - параметры распределения. Закон распределения фаз импульсов часто принимается равномерным, а длительностей - усеченным нормальным

  [ С exp^{[ - (} r „ ^- m T ^)2]

  W ( T n ) = 1         2 ^ 2        ’ 1 "  n "  ²            (6)

  1 0;                т <  t_v n> >  2_г,

  где С - нормирующая константа, определяемая границами усечения, m , о - моменты исходной (неусеченной) гауссовской функции.

  2. ВЫБОР ОПТИМАЛЬНОГО ПРЕДСТАВЛЕНИЯ СИГНАЛОВ И ПОМЕХ В ЗАДАЧАХ АМПЛИТУДНОЙ СЕЛЕКЦИИ

  На вход приемного устройства поступает смесь сигнала s ( t ), суммы сосредоточенной и флуктуационной помех n ( t ) с ИП u ( t )

  z ( t ) = 5 ( t ) + n ( t ) + u ( t ) .                        (7)

  В наиболее общем виде рассматриваемый здесь класс нелинейных фильтров можно представить структурной схемой, показанной на рис. 1. Оператор F задает отображение множества входных воздействий вида (7) на множество функций некоторой (в общем случае - новой) переменной v ( Э ), в котором обеспечена наилучшая селекция сигнала и импульсных помех, определяемая оператором К . Обратный оператор F обеспечивает формирование оценки

  5> ( t ) = z ( t )^{- u} ( t )

  остатка смеси (7) с подавленной ИП

  z 0 ( t ) = ⁵ ( t ) ^{+ n} ( t )                                 ⁽⁸⁾

  по селектированной функции v 0 ( Э ) , а оператор W описывает линейный фильтр, обеспечивающий оптимальную оценку полезного сигнала s € ( t ) в смеси (8).

  
  
  

  Рис. 1

  
  

  £ ² = ( 5 - € ( 2 , (10) где

  € = F - 1 KF z . (11)

  В задачах обработки изображений, а также при приеме непрерывных сообщений, часто используется критерий приближения в равномерной метрике

  ^Л 2 = max | ^{5 (} t ^{)- € (} t ) 2 , ⁽¹²⁾ t , п

  где П - пространство реализаций.

  В отличие от задач оптимальной линейной фильтрации, где выбор базиса для представления сигналов не влияет на результат и определяется лишь удобствами реализации (например, применением БПФ), качество амплитудной селекции сигналов и ИП существенно зависит от такого выбора. Например, селекция с помощью ограничения или бланкирования ИП эффективна во временной или пространственной области, где сигнал и помеха различаются по амплитуде и длительности, и теряет смысл в спектральной области, где их спектры сходны.

  Таким образом, возникает задача выбора оптимального отображения F , при котором с учетом вида оператора селекции К обеспечивается наиболее эффективное подавление ИП по критерию (9).

  Как и в других задачах оптимальной обработки сигналов, из общего критерия (9) можно вывести более простое и удобное для синтеза алгоритмов решающее правило. Оно зависит от выбранного способа селекции (оператора К ).

  Нетрудно показать, что при использовании ограничения указанное правило сводится к максимизации показателя селективности

  Y = PjP o , (13)

  где Р и P 0 - усредненные по реализациям пиковые мощности ИП и остаточной смеси вида (8) в области отображений (функций v ( Э )).

  При использовании бланкирования необходимо минимизир о вать среднюю ширину ИП в области отображений Э _п .

  Обоим правилам удовлетворяет отображение F , обеспечивающее максимальное увеличение амплитуды и уменьшение длительности ИП или площади пораженного ИП участка изображения в смеси (7). Детальный анализ показывает, что такое отображение не может быть линейным и должно зависеть от амплитуды или мгновенной мощности z ( t ) (в

  
  

противном случае, возможно пропорциональное увеличение пиков помехи и сигнала). Кроме того, должна быть простой и однозначной реализация обратного оператора F . Этому требованию в наибольшей степени удовлетворяют унитарные (ортогональные) операторы.

Таким образом, отображение F, удовлетворяющее поставленным требованиям, следует искать в классе операторов с унитарной нелинейностью. Один из классов таких операторов для функций непрерывных аргументов рассматривается в нелинейной квантовой механике [9], нелинейной оптике [10] и описывается эволюционными уравнениями шре-дингеровского типа i — + аАТ + f (Т) = 0,                (14)

дп где а - постоянный коэффициент, А - оператор Лапласа по координатам 11 и 12 , f - функция, определяющая вид нелинейности, Т(п, t) - комплексная функция, значение которой при п= 0 и некотором n= l соответствует сигналам на входе и выходе блока F:

Т ( 0, t ) = z ( t ) ; Т ( l , t ) = v ( t ) .                (15)

Уравнение (14) задает отображение функций, определенных в области Т , которое описывает преобразование сигнала z ( t ) в некотором двумерном пространственно распределенном нелинейном фильтре.

При этом обратное отображение задается сопряженным уравнением

• - i — + аАТ + f (Т) = 0,(16)

дп где

Т(0, t) = v0 (t); Т(l, t) = z0 (t),(17)

т.е.

F = F*.(18)

Непосредственная реализация указанных операторов в аналоговой форме возможна для двумерных и одномерных полей оптического и некоторых других ( например, СВЧ ) диапазонов электромагнитных волн в нелинейных диэлектрических средах. При определенном выборе нелинейности, описываемой функцией f ( Т ) в (14), можно за счет само-воздействия волн обеспечить селективную фокусировку участков поля с аномально большой интенсивностью, обусловленной наложением ИП, и тем самым - увеличение показателя селективности (13). Однако, возможности варьирования и оптимизации параметров нелинейного оператора в этом случае весьма ограничены. Поэтому основное применение рассматриваемый метод может найти при дискретной и цифровой обработке сигналов.

Для такой реализации оператор F целесообразно представить, используя метод расщепления по физическим факторам [11,12], в виде произведения линейных ( G k ) и нелинейных ( H k ) операторов вида n

F = П GkHк [Тк ].(19)

к = 1

Каждый из линейных операторов G k реализуется звеном с передаточной функцией

Gk (i®)= exp {-ш(®2 + ®22)А%},(20)

которой соответствует импульсная характеристика (функция Грина линейной части уравнения (14)) ia k ( t ',² + t 2 )

gk (t) = g о к exp —2—,(21)

где to = ( Ю 1 , © 2 ) - вектор частот, n - число пар звеньев,

^А П к = П к + 1 ^- П к , _ 1

g 0 к = ( ^{4 п А} П к ^{a i}X ²,                        ⁽²²⁾

1 а_к =---------.

2 А п _к a

Нетрудно заметить, что линейный интегральный оператор с ядром (21) представляет собой известное преобразование Френеля [2] и , таким образом, указанные линейные звенья - это фильтры Френеля. Нелинейные операторы H k [ T k ] в (19) соответствуют умножению функции T_k ( т ) = T ( n_k , T ) на зависящие от нее коэффициенты преобразования

H к [ Т к ] = exp [ if ( Т к ) ] .                  (23)

Сопряженный оператор вследствие уже упоминавшегося свойства унитарности представляется в виде

n

• F * [ Т ] = П H * [ Т к ] G k .                  (24)

• 3.    ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ФИЛЬТРА

к = 1

Как видно из (20) и (23), рассматриваемые линейные и нелинейные звенья имеют единичные, не зависящие от частоты модули коэффициентов передачи и в совокупности образуют некоторый нелинейный фазовый фильтр с распределенными параметрами. Для его реализации в цифровой форме производится обычная дискретизация переменных t ₁ , t ₂ и соответствующих им частот to 1 , оу . Нелинейное преобразование (23) реализуется непосредственно в области определения сигнала, а преобразование Френеля - с помощью одного или двух двумерных БПФ [2,12]. При втором способе затраты времени больше, но зато выше точность.

Минимальное число пар звеньев, необходимое для реализации предъявленных к оператору F требований n = 1. С увеличением n отображение F становится менее критичным к форме ИП.

При n =1 результат отображения F можно записать в явном виде:

v ( t ) = g 0 JJ exp

T a (t - r(2

¹f [ z ^{( t} ) ] ^x

x z ( t ) d r 1 d r 2 .

Для определения функции f в (25), доставляющей максимум показателя селективности (13), необходимо учесть исходное требование к нелинейному оператору Н: селективное действие на ИП без существенного изменения остальных компонент смеси z(t), которые предполагаются слабыми по сравнению с ИП u (t). Это достигается при условии

(f [z0 (t)](<<(f [u (t)](. (26)

При этом знаменатель отношения (13) практически не зависит от выбора f и достаточно максимизировать пиковую мощность отклика (25) на ИП , т.е. при z (t) = v (t). Пик (25) в этом случае достигается при t = 0 и равен v (0) = g0 JJ exp

T

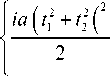
zf©u ( t ) ] •u ( t ) dt 1 dt 2 .

Для определения максимума пиковой мощности I v (0) I используем известное неравенство для интеграла от любой комплексной функции Q ( t )

JJ Q ( t ) ^dt1 ^dt 2

T

^ JJ ( Q ( t ) ( ^dt1^dt 2 , T

Выбор фазового фильтра обусловлен, как уже отмечалось, требованием унитарности оператора F .

В полностью согласованном фильтре величина U _m имела бы значение

которое переходит в равенство при Q ( t ) = I Q ( t ) I . В силу него для отдельной реализации ИП u ( t ) указанный максимум достигается (в предположении, что f - вещественная функция ) при

a ( t 2 + t 22 )

—2—+ft u (t)]+Ф (t) = 0

и равен

U m = max

2        „Г 1 2

( v (0)( =(g0 (   JJ( u (t)( dt 1dt2 ,

где ф ( t ) = arg u ( t ).

Условие (29) есть условие согласования фильтра, имеющего импульсную характеристику (21) с ИП u ( t ) по фазе.

Pu = |v (0)| = gcl2 J w (®) JJ exp

R

I T

ia ( t 1 ² + 1 ₂ ² )

U 2 = ( g 0 ( ² ■

2          1 2

JJ ( ^u ( t ) ( dt i dt 2    = ( g 0 ( E u ,

. T                               ]

где E u - энергия u ( t ). Ясно, что различие между (30) и (31) несущественно.

Таким образом, предлагаемое преобразование ИП основано на развитии известных методов сжатия частотно-модулированных импульсов в согласованных фильтрах, но в отличие от них здесь модуляция ставится в зависимость от интенсивности сигнала и фильтр является двумерным.

Как ясно из уравнения (29), оптимальная функция зависит от параметров импульса. Если они случайные, необходимо искать максимум пиковой мощности путем усреднения (27) с учетом их распределений:

if Г u ( t , ® ) ] - u ( t , ® ) dt 1 dt ₂ ( d ® ,

где w ( ® ) - плотность вероятности вектора параметров, R - их область определения.

Рассмотрим параметрическую оптимизацию функционала (32). Пусть функция f определяется заданным заранее аналитическим выражением, содержащим вектор неизвестных параметров в ,

f (u ) = J (u, в).

Тогда точку экстремума функционала (32) можно найти обычным методом, по нулям производных. Приравнивая нулю производную выражения (32) по параметрам в после несложных преобразований получаем систему уравнений для оптимальных значений в

J W (®) Re JJ JJ exp {i [Ф (t1, ®) - Ф (12, ®)]}u (t1, ®) u * (12, ®) RTT

df Г( u (ti, ®), в (]

5P k

dt 1 dt ® dt ₂ dt ₂ © d ® = 0,

где k = 1, 2,..., n;

,         a ( t 2 + 1 22 )

ф ( t , ® ) =2—’-+ f ( u , ® ) + ^ ( t ) .

Способ решения указанных уравнений зависит от конкретного вида функций f . Пусть, например,

N f ((u (, P ) = E вМ,                  (35)

k = 0

Подставляя (36) в (33) и линеаризуя полученные уравнения путем разложения экспоненты в ряд, после ряда преобразований получаем систему линейных уравнений вида

N - 1

E a /k ^ k = b ^, k = 0

или, в матричной форме тогда где

A P = b ,                                   (38)

df = \«t

5Pk 1 1

a/k = Re {i JJ JJ exp{ia ( t2 + t 2 - T - T 2 )}[ vi+k+2 - М/+k+2 ] dt1dt2 dT1dT 2 },

TT bl = Re JJ JJexp{ia (t2 +12 -т2 -т2)}al+2 (t1,12, т1, т2)dt 1 dt2dr dr2.(40)

TT

В выражения (39), (40) входят моментные функции

^/+k+2 (ti, t2) = J(u (ti, ®)(‘+k u (ti, ®)u * (t2, ®) w(®)d®,

R vl+k+2 ( t1, t 2 ) = J( u ( t1, ®)(l ( u ( t1, ®)(ku ( t1, ®) u * ( t2, ®) w (®) d ®, R

^а / + 2 ( t 1 , t 2 ) = J ( u ( t 1 , ® ) ( l u ( t 1 , ® ) u * ( t 2 , ® ) w ( ® ) d ® , R

При | A | ^ 0 уравнения (38) имеют решение

P op. = A "b . (44)

Поскольку аналитическое вычисление таких интегралов громоздко или затруднено, для расчета коэффициентов (39), (40) целесообразно использовать численные методы.

Алгоритм фильтрации и условия оптимизации фильтра для одномерных (временных) сигналов легко получаются из приведенных выше как частный случай.

• 4.    РЕЗУЛЬТАТЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

С целью проверки эффективности разработанного метода подавления ИП было проведено сравнительное статистическое моделирование, в процессе которого воспроизводились реализации сигнала и ИП, осуществлялось подавление ИП рассматриваемым и известным методами и определялись показатели качества обоих методов. При моделировании реализаций ИП задавались характеристики, указанные в п.1, для флуктуационной помехи была принята обычная модель в виде белого гауссовского шума, а для сигнала (изображения) - в виде гауссовского случайного поля с корреляционной функцией экспоненциального вида (воспроизводился фрагмент изображения размером 256x256 отсчетов). Параметры нелинейной фазовой функции, аппроксимированной полиномом второй степени вида (35), были рассчитаны путем численного решения системы уравнений (38) с коэффициентами, найденными по формулам (39) - (43). В качестве не- линейного преобразования К ( в области образов Френеля ) выбрано, как наилучшее, бланкирование с экспериментально подобранным оптимальным порогом. Результаты подавления ИП оценивались по двум критериям - СКО (10) qе = е и квадрату модуля максимального отклонения (12) qд = А , а затем сравнивались с аналогичными показателями, полученными путем моделирования одного из наиболее эффективных известных методов подавления ИП на изображениях - медианной фильтрации [3] при тех же характеристиках сигнала и помех.

На рис.2 и 3 показаны полученные зависимости указанных показателей от среднего значения ширины импульса помехи m ® по одной из координат для случая, когда дисперсия ширины составляла 10% от m ® . Зависимости для рассматриваемого метода показаны сплошными линиями, а для известного (медианного фильтра) - штриховыми. Размер окна при медианной фильтрации составлял 3 x 3 отсчета и его увеличение при выбранных параметрах ИП и сигнала не приводило к улучшению качества подавления ИП.

Из приведенных зависимостей видно, что для ИП малого размера по сравнению с рассматриваемой областью изображения, т.е. близких к точечным, предлагаемый метод, как и следовало ожидать, не дает выигрыша или даже имеет проигрыш (по второму критерию), так как нет резервов дополнительного сжатия ИП и более эффективной является обычная медианная фильтрация (или другой извест- ный метод, например, интерполяция по соседним отсчетам). С увеличением размеров ИП все более заметным становится выигрыш, достигаемый предлагаемым методом по сравнению с известным, так как проявляются преимущества сжатия ИП. Например, при mΘ = 10 достигается выигрыш по СКО около 8 дБ, а по второму критерию - 6,5 дБ. Результаты, полученные при других значениях параметров ИП и сигнала, имеют аналогичный характер.

q,X 104

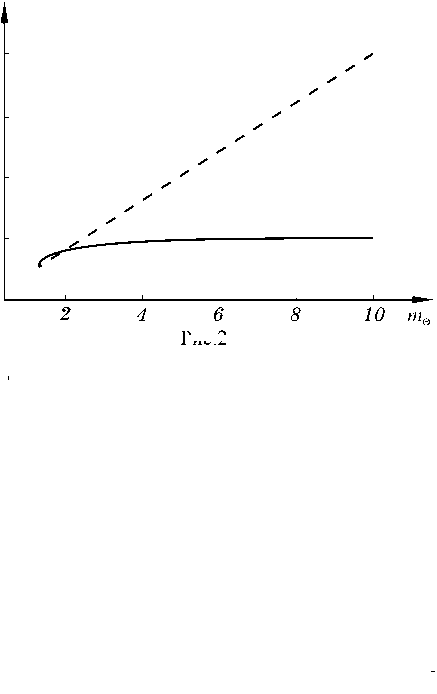
Рис.2

Q±

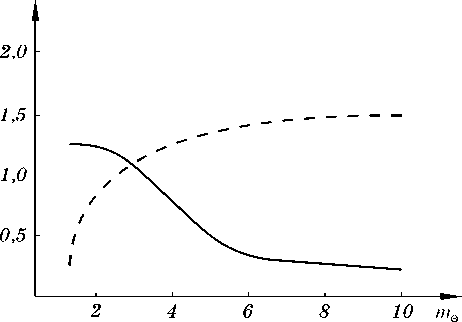
Рис.3

В заключение необходимо отметить , существуют резервы дальнейшего повышения эффективности подавления ИП предложенным методом за счет совершенствования вида аппроксимации нелинейной фазовой функции фильтра и увеличения числа его звеньев.

Для более обоснованных рекомендаций по выбору этих и других параметров необходимы дальнейшие эксперименты на реальных изображениях с использованием различных, в том числе субъективных критериев оценки их качества.