Метод полного разложения мостиковых соединений в задачах анализа связности радиально-кольцевых структур систем оповещения населения

Действующие системы оповещения населения (СОН) МЧС России построены по радиально-узловому принципу, основным недостатком которого является отсутствие кольцевых связей между управляемыми пунктами оповещения. Такое организационнотехническое построение (ОТП) СОН не способствует повышению связности управляющего центра оповещения (ЦО) с управляемыми пунктами оповещения (ПО). Поэтому при модернизации существующих и создании новых СОН предлагается применение радиально-кольцевого принципа ОТП, при реализации которого устанавливаются дополнительные кольцевые связи между управляемыми ПО. Вследствие этого вероятность связности управляющего ЦО с управляемыми ПО увеличивается более, чем на один порядок.

Однако задача анализа связности управляющего ЦО с управляемыми ПО для таких структур СОН относится к классу трудно реализуемых задач [1, 2].

Для устранения указанной трудности предлагается использовать метод полного разложения мостиковых соединений (МПРМС), особенность практического применения которого можно рассмотреть применительно к радиально-кольцевой структуре СОН, представленной на рис 1.

В такой модели СОН использована следующая последовательность нумерации ее элементов: слева направо по часовой стрелке от первой вершины v ₁. При этом вначале нумеруются вершины V = { v_i } ( i = 1,4 ), затем радиальные ребра L p = { 1 ц } ( Ц = 5,8) и далее кольцевые ребра L k = { 1 ц } ( Ц = 9,12).

Особенность рассматриваемой модели СОН состоит в том, что она включает одну истоковую (нулевую) вершину v ₀, соответствующую управляющему ЦО, и 4 стоковых в ер шины нижестоящих пунктов оповещения v_i , i = 1,4, соответствующие управляемым ПО.

Радиальное ребро l ₅ ^p , непосредственно соединяющее в ершину — исток v ₀ с вершиной истоком v_i ( i = 1,4), есть ребро непосредственной связи (РНС).

В общем случае в качес тв е РНС может быть принято любое ребро 1 ц ( Ц = 5,8) в зависимости от заданного i -го значения стоков ой в ершины v_i ( i = 1,4).

Кольцевые ребра Ц ( Ц = 9,12 ) в представленной модели СОН являются мос ти ковыми соединениями между вершинами v_i ( i = 1,4), и поэтому подлежат разложению по модулю 2 (работоспособное или неработоспособное состояние Ц -го соединения.

Для рассматриваемой модели СОН аналитическое выражение МПРМС будет иметь следующий вид [2]:

P 1 = Ё p ( Г ) p ( G ) , (1) i = 1

где p ( Г_i^k ) — вероятность нахождения кольцевых ребер в состоянии Г_i^k ;

p(Gi) = p(G / Гik) — условная вероятность связно- сти вершины — истока v0 с вершиной стока v1 (vi) при принятии гипотезы Гk1(Гik).

Вероятность состояния (гипотезы) Гi определяется как p (rk)=n p (lk) n q (ik),         (2)

^V i Ц е N 1          Ц е N ₂         ’                ^{V 7}

где N ₁ и N ₂ — обозначение соответственно работоспособных и отказавших кольцевых соединений, составляющих гипотезу Г_i^k ( N ₁ + N ₂ = N );

p ( Ц ) — вероятность нахождения кольцевого соединения 1 Ц в работоспособном состоянии, q ( Ц ) = 1 - p ( Ц ).

Алгоритм расчета полной вероятности связности (1) вершины 9 ₀ с кольцевыми вершинами 5 1 ( б Ц =2-^ ) , (рис. 1) сводится к последовательному выполнению следующих аналитических операций.

Вначале определяется число состояний кольцевых ребер, которое равно Г^k = 2⁴ = 16, в том числе:

kk

± 1      '9 '10 '11 '12     2     '9 '10 '11 ‘12’ kk

• 3    99  40  41  42    4    99  40  4142’

kk

1 5    99  40  41  42    6    f9  40  4142’ kk

• 7    f9  40  41  42    8    99  40  4142’

kk

• 9      9   10   11   12    10     9   10   1112

kk

• 11     9   10   11   12    12     9   10   1112

kk

13     9   10   11   12    14     9   10   1112

kk

15     9   10   11   12    16     9   10   1112

Затем, с учетом состояний кольцевых ребер (3) выражается событие E _0,1 связности вершин ϑ ₀ и ϑ ₁ анализируемой РКС СОН G (рис. 1) следующим образом:

E 0,1 = Е ^ri • G i ,                (4)

i = 1

где G_i = G / Г_i^k — i -й условный СГ ДС, полученный в результате преобразования исходной РКС G (рис. 1) в соответствии с состояниями (3) его кольцевых ребер kk .

L    ^{{ 1} Ц = 9,12 }

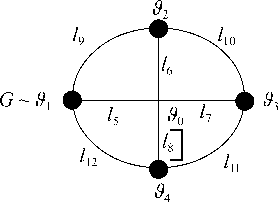
Рис. 1 Модель радиально-кольцевой сети с четырьмя радиальными направлениями

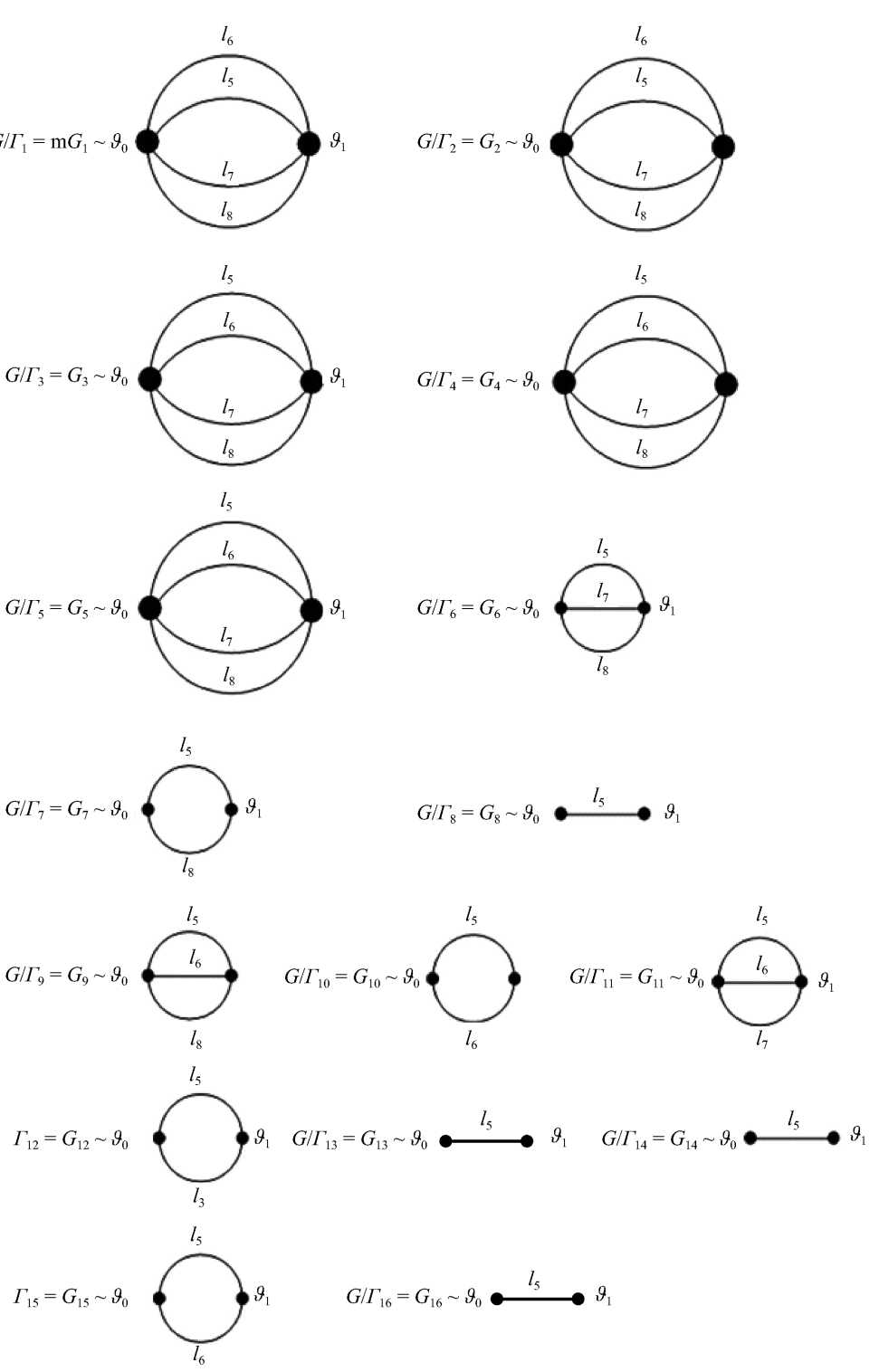
Полученные в результате выполнения этих аналитических операций условные СГ ДС G / F i = { G i = 516 } представлены на рис. 2.

l 5

l 5

l 7

l 7

l

l

l

l

l

l l5

l l7

l

l

l l5

l 5

l 6

l 6

l 6

l 6

l 6

ϑ 1

G / Г 6 = G 6 ~ ϑ

~ ϑ

G / Г 10 = G 10

G / Г ₁ = m G ₁ ~ ϑ ₀

G / Г 3 = G 3 ~ ϑ 0

G / Г 5 = G 5 ~ ϑ 0

l ₅

l ₅

ϑ 1

ϑ 1

ϑ 1

G / Г 7 = G 7 ~ ϑ 0

G / Г 9 = G 9 ~ ϑ 0

Г 12 = G 12 ~ ϑ 0

Г 15 = G 15 ~ ϑ 0

l 6

l ₅

l l5

l l5

ϑ 1

l

G / Г 8 = G 8 ~ ϑ 0       ⁵        ϑ 1

l ₅

G / Г 11 = G 11 ~ ϑ 0       ^{l 6}       ϑ ₁

l ₇

l 5

ϑ 1    G / Г 14 = G 14 ~ ϑ 0              ϑ 1

ϑ 1

G / Г 16 = G 16 ~ ϑ 0

ϑ 1

G / Г 2 = G 2 ~ ϑ 0

G / Г 4 = G 4 ~ ϑ 0

l ₅

l ₅

l 6

l 6

ϑ 1

l ₅

G / Г 13 = G 13 ~ ϑ 0

Рис. 2. Разложение РКС СОН G (рис.1) по состояниям кольцевых ребер

Согласно гипотезам (3) и структурам условных

СГ ДС G/Г! = | G/Г. — 1= G (рис. 2), событие связности (4) выражается ⁵ в следующем виде:

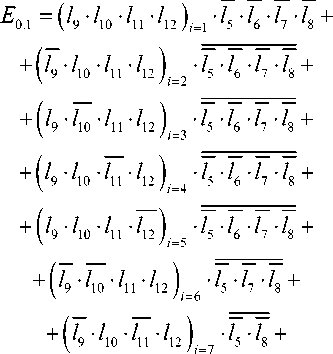
+  9 40 41 42      5 + i=8

+ 9 40 41 42       5 *6 48 + i=9

+ 9 40 41 42       5 l6 + i =10

TA +

+ 9 40 41 42       5 *6 71 + i =11

+ 9 40 41 42       5 l8 + i =12

TA +

+ 9

+                + i=14

^(lTT TA TIT

+ 9 <ю

-1A -I

⁺9 40 41 42        5.

i =16

В соответствии с равенством (5), полную вероятность связности вершин ϑ₀ и ϑ₁, анализируемой РКС СОНG (рис. 1), можно определить следующим образом: см. (6).

Допустим, что p(l_ƺ=5^—_,1^–₂). Тогда равенство (6) примет вид:

P_0,1 = p⁴ . (1 – q⁴) + 4 . p³ . q . (1 – q⁴) +

+ 3 . p² . q² . (1 – q³) + 2 . p² . q² . (1 – q²) +    (7)

+ p² . q² . p + 2 . p . q³ . p + q⁴.

Если принять, что p = 0,9 (q = 0,1), то согласно формуле (7), P_0,1 = 0,99870093.

Таким образом, показана возможность применения МПРМС для расчета связности радиально-кольцевых структур в СОН МЧС России.

P1 = (p 9 • P10 • p 11 • P12) i=1 • q 5 • q 6 • q 7 • q 8 ^{+ +}(q 9 • P10 • P11 • p 12 )i=₂• q 5 • q 6 • q 7 • q 8 ⁺

+(p 9 • q_№ • P11 • p 12) i=₃• q 5 • q 6 • q 7 • q 8 ⁺

• ⁺(p 9 • p_№ • qn • p 12 )i=₄• q 5 • q 6 • q 7 • q 8⁺

• ⁺(p 9 • p_№ • p 11 • q12) i=₅• q 5 • q 6 • q 7 • q 8⁺

• ⁺(q 9 • q 10 • ph • p12) i=6 • q 5 • q 7 • q 8^{+ +}(q 9 • p_№ • qn • p12 ) i=7 • q 5 • q 8^{+ +}(q 9 • p_№ • ph • q 12 )i=8 • p 5^{+ +}(p 9 • q 10 • qn • p 12) i=9 • q 5 • q 6 • q 8^{+ +}(p 9 • q 10 • ph • q 12) i=_to • q 5 • q 6^{+ +}(p 9 • p_№ • q 11 • q12) i=_n • q 5 • q 6 • q 7^{+ + (q} 9 • ^q10 • ^q11 • ^p12 ) i=₁₂• ^q 5 • ^q 8 ^{+ +}(q 9 • q_№ • p 11 • q12) i=13 • p 5^{+ +}(q 9 • p 10 • qn • q12) i=14 • p 5^{+ +}(p 9 • q 10 • qn • q12) i=15 • q 5 • q 6^{+ + ( q} 9 • ^q10 • ^q 11 • ^q12 ) i=₁₆• ^p 5-

• При этом из анализа рассмотренного примера можно заметить, что вероятность связности в РКС СОН (рис.1) относительно СОН, построенной по радиально-узловому принципу без кольцевых связей, увеличилась практически на 2 порядка.