Метод получения совокупности конечного объема средневзвешенных напряжений в деталях машин

Получение выборки средневзвешенных напряжений. Для получения выборочного распределения действующих напряжений деталей необходимо иметь статистический ряд средневзвешенных значений σсв (рис.1), определенных на нескольких деталях и в разных условиях работы, учитывающих различные климатические условия, технические состояния машин, режимы работы и т.д. Поэтому каждое распределение амплитуд σа по времени (проанализированная осциллограмма одной детали) необходимо привести к симметричному циклу [1, 2, 3] и заменить одним средневзвешенным значением. Тогда m    nm св               ai i , i=1

где σ а – амплитуда действующего напряжения; m – показатель угла наклона кривой усталости; n – число циклов нагружения; t i – доля i -й амплитуды (относительное число циклов)

n

• 2 t i = i i = 1

Формирование выборки σ св в реальных условиях очень трудоемкая и дорогостоящая задача, так как требуется провести тензометрирование однотипных деталей на представительной партии машин (например, одноковшовых экскаваторов), которые могут быть территориально рассредоточены. Для снижения трудоемкости работ, как один из вариантов, предлагается выполнить имитацию различных условий работы машины [2], при учете влияния ряда факторов, влияющих на нагруженность деталей одноковшового экскаватора. В качестве таких факторов могут выступать: опыт работы машиниста (стаж 1-3 года; 3-5 лет;

Рис.1. Плотности распределения амплитуд для однотипных деталей f(σ а ) и плотность распределения средневзвешенных напряжений f(σ св )

5-10 и более лет); качество изготовления экскаватора (хорошее, удовлетворительное, плохое); грунтовые условия (низкие, средние, высокие температуры; структура грунта); отношение машиниста к машине (хорошее, удовлетворительное, плохое); выполнение ремонта и технического обслуживания (хорошее, удовлетворительное, плохое) и др. В связи c этим для получения данных по нагруженности деталей необходимо пользоваться распределением средневзвешенных напряжений, полученных по выборке однотипных деталей, а не амплитудными значениями в функции времени для одной детали.

Получение совокупности средневзвешенных напряжений . Предлагаемый в работе [4] метод получения СКО через ПСКО по малой выборке с помощью распределения абсолютных разма-хов F(W) применим для любого распределения исходной совокупности. Известно [1], что для аппроксимации данных по нагруженности используется распределение Фишера-Типпета II рода:

P ( x ) = £

-

. (c—x) ь                                                   b a - функция распределения; p(x) =—(—

a

—

a

x ) b ^—1 £

-

-(c—x) b a – плотность распределения.

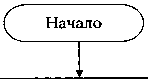
(>-!)!(»-i + 1)!

Ввод данных:

n, NncKO> Хь Хг>..., Хп, А, В, а, Ь,

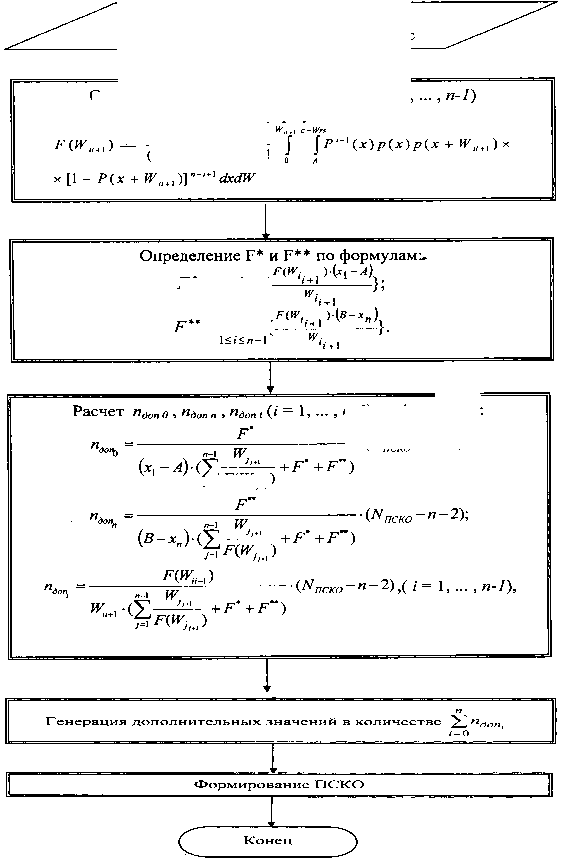
Рис. 2. Блок-схема алгоритма моделирования промежуточной совокупности конечного объема на основе малой выборки с помощью распределения абсолютных размахов

Определение вероятностей F(W"u₊i), (j= 1, по формуле n'.

F = min {

= max {

и-7) по формулам:

О^пско — п — ^)\

Для проведения вычислительного эксперимента в качестве СКО взята совокупность объемом N СКО = 100 средневзвешенных напряжений в опасном сечении рукояти одноковшового экскаватора [3], которые были получены в результате анализа данных по нагруженности рукояти. Эксперимент проведен по алгоритму, представленному на рис.2, повторён 50 раз для объема выборки n=5. Малые выборки получены из СКО с помощью ПЭВМ методом простого случайного выбора. Априорный интервал изменения характеристики [ A , B ]=[40,3; 52,4]. Дополнительные значения генерировались как равномерно распределённые случайные числа.

На рис.3 представлены эмпирические функции распределения исходной совокупности и одной из моделированных.

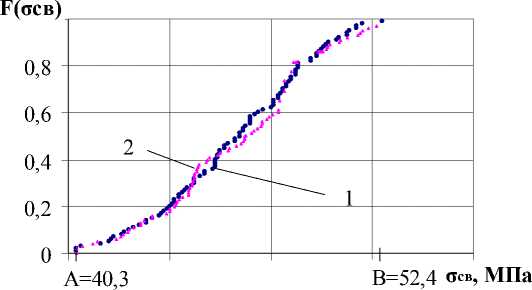
Рис. 3. Эмпирические функции распределения совокупностей конечного объема средневзвешенных напряжений в опасном сечении рукояти одноковшового экскаватора: 1 – исходная;2 – моделированная

Однородность исходной совокупности и ПСКО оценена по критерию Вилкоксона [5]. Для проверки гипотезы о том, что функции распределения генеральных совокупностей, из которых извлечены выборки, совпадают по всей области их определения, применен критерий Смирнова-Колмогорова [6].

В результате проведенного эксперимента получено количество ПСКО, однородных с исходной совокупностью по критерию Вилкоксона для уровня значимости α=0,01, N B =40 штук (80%); количество ПСКО, имеющих одну генеральную совокупность с исходной по критерию Смирнова-Колмогорова для уровней значимости α=0,01 и α=0,001; N K = 48 штук (96%).

Выводы . Проведенный вычислительный эксперимент показал, что 80% моделированных совокупностей конечного объема по малым выборкам объема n = 5 однородны с исходной совокупностью и 96% имеют с ней общую генеральную совокупность.

Таким образом, метод статистического моделирования с использованием распределения абсолютных размахов позволяет получить параметры закона Фишера-Типпета для СКО деталей со средневзвешенными напряжениями по малой выборке объема n = 5 с помощью промежуточной совокупности конечного объема.