Метод порогового подавления шума в сигнале на основе вейвлет-преобразования

Прогресс вычислительной техники и, как следствие, ускоренный процесс информатизации общества делают актуальной проблему создания и реализации систем цифровой обработки сигналов в режиме реального времени, являющейся краеугольным камнем в сфере информационной безопасности.

Системы распознавания, передачи и обработки сигналов, функционирующие в неблагоприятных условиях, таких как, например, движущийся автомобиль, большое число сторонних источников сигнала и т.д., оперируют с большим числом окружающих шумов, что приводит к существенному понижению эффективности подобного рода систем.

2.    Постановка задачи исследования

На протяжении многих десятилетий и по настоящее время основным средством анализа сигналов является гармонический анализ, математической основой которого является преобразование Фурье. На практике, однако, недостатки анализа Фурье приводят к потере информации о временных характеристиках обрабатываемых сигналов и, что следует особо подчеркнуть, делают его малопригодным для обработки нестационарных сигналов [1; 2].

Подобные ограничения приводят нас к поиску новых технологий анализа и обработки сигналов и делают актуальной задачу разработки методов и алгоритмов для решения задач автоматического распознавания речи, в частности, ключевой проблемы в данной области – очистки сигнала от шума с сохранением особенностей сигнала.

3.    Обоснование метода решения задачи

Речевая информация крайне важна для систем распознавания, поэтому классический метод подавления шумов основывается на спектральном анализе и удалении высокочастотных составляющих из спектра сигнала, так как основные частотные компоненты расположены, как правило, в низкочастотной области спектра. Именно вейвлет-преобразование, предполагающее разложение сигнала в базис функций, характеризующих как частотную, так и временную составляющую, открывает новые подходы к очистке от шума [34]. Шумовые компоненты можно рассматривать в виде множеств локальных особенностей сигналов. Задавая некоторый порог для их уровня и срезая по нему детализирующие коэффициенты, можно не только уменьшать уровень шумов, но и устанавливать пороговые ограничения на нескольких уровнях разложения с учетом конкретных характеристик шума и исследуемого объекта.

Среди наиболее известных существующих методов подавления шумов с помощью вейвлетов: Малла, Донохо и метод инвариантной пороговой фильтрации TIS [5]. Метод Малла основан на очистке от белого шума путем извлечения корня из максимума вейвлет-преобразования с разным масштабом. Он позволяет максимально точно сохранять основные особенности сигнала, однако крайне сложен для аппаратной реализации [2]. Метод VisuShrink (Донохо), использующий пирамидальные фильтры и лишь один порог, не рассматривает различные характеристики полос частот [5].

Пусть дан зашумленный сигнал y n = x n + b n для n = 1 ,N , где b n - белый гауссовый шум и нужно найти хорошую оценку x от x = { x n } n ₌^ . Таким образом, нашей целью является нахождение такой функции зашумленных данных F ⁽ y ) = ( f n ⁽ y ))_№   = x , которая бы позволила минимизировать ⁿ среднеквадратическое отклонение (MSE):

1 ² 1 ^{N 2}

MSE = n x -x = ^ g| x n -x ,|.   (1)

Так как в большинстве случаев отсутствует доступ к исходному сигналу, то невозможно вычислить и отклонение. Однако, используя лемму Стейна [6], можно заменить выражение, содержа- щее неизвестную переменную x, другим выражением, содержащим только известную переменную y.

Пусть F(y) векторная функция, такая что L{dfn (У )/ дУп |} <”для n = 1,N. Тогда под шумом можно подразумевать следующее выражение:

L{fn (У )xn} = L{fn (У )Уп}-^2 Lfy) |, (2) ⎩ ∂yn ⎭ где l{*} - линейный оператор.

Метод порогового шумоподавления на основе генетических алгоритмов (ПШП-ГА) состоит из трех основных этапов:

• 1)    прямого вейвлет-преобразования (декомпозиции), на котором исходный сигнал разбивается на N частотных полос вейвлетной области по методу Малла [2];

• 2)    очистки от шума с помощью пороговой функции;

• 3)    обратного вейвлет-преобразования (реконструкции).

Хороший выбор параметров, таких как вейвлет-функция, уровни декомпозиции и ключевой параметр – порог, является критичным для хороших результатов. Как правило, данные параметры выбираются эмпирически, что не всегда может гарантировать оптимальность шумовой очистки. Для решения этой проблемы, предла- гается использовать генетические алгоритмы (ГА).

Генетический алгоритм представляет собой метод, отражающий естественную эволюцию методов решения проблем. Это процедуры поиска, основанные на механизмах естественного отбора и наследования. В них используется эволюционный принцип выживания наиболее приспособленных особей для получения наиболее близких приближений к решению и ГА по достоинству заслужили популярность во многих приложениях, требующих оптимизации решения без наличия теоретических знаний в области данной проблемы или там, где моделирование или понимание затруднены [3].

Очень важным понятием в генетических алгоритмах является функция приспособленности . Приспособленность, в самом общем случае, – это среднеквадратическое отклонение между исходным и конечным сигналами, как показано в уравнении (1), но так как, было отмечено выше, исходный сигнал часто не известен, то и среднеквадратическое отклонение не может быть вычислено. Таким образом, мы берем коэффициенты корреляции между исследуемым и обработанным сигналами, которые вычисляются по формуле:

F =

^N вых ¹

N , вых m=1

N "I

Z У п x n + m n = 0

Обычно коэффициент корреляции прямо пропорционален отношению «сигнал-шум» (SNR), ввиду этого его целесообразно выбрать в качестве функции приспособленности.

После генерации исходного множества хромосом, происходит селекция особей по рассчитанным значениям функции приспособленности с помощью комбинированного рулеточно-турнирного метода, когда пары родительских особей выбираются случайным образом, после чего из каждой пары выбирается особь с наибольшим значением функции приспособленности.

Недостатком классического генетического алгоритма является возможность того, что новая популяция P ( k + 1 ) не всегда содержит особь с наибольшим значением функции приспособленности из предыдущей популяции P ( k ) . Используемая в нашем методе элитарная стратегия позволяет предотвратить потерю такой особи [3].

После выбора всех родительских особей, участвующих в процессе эволюции, начинается скрещивание, являющееся ядром ГА и позволяющее найти оптимальное решение во всей области определения. Помимо скрещивания используются еще две операции получения потомков, отличающихся от родительских особей: мутация и инверсия. Они помогают избежать преждевременной сходимости. После эволюционных операций селекции, скрещивания и мутации, создается новое поколение. Процесс эволюции повторяется до тех пор, пока не достигается оптимизационный критерий (максимальное число итераций, время или невозможность улучшения лучшей особи).

В рамках нашего метода посредством генетических алгоритмов вычисляются следующие параметры: значение пороговой функции и уровни декомпозиции.

Пусть W ( • ) и W ^{- 1} ( - ) обозначают операторы прямого и обратного вейвлет-преобразования. Пусть T ( -Д ) – оператор очистки от шума с жестким или мягким порогом X . Тогда описанная выше процедура очистки от шума может быть представлена в виде:

D = W (У); (4) 6 = T (zA ); (5) R = W —1 (9), (6)

или данный алгоритм может быть представлен как функция входных коэффициентов шума:

X = F ( y ) = RO ( D ) .

Коэффициенты вейвлет-преобразования на каждом этапе выполнения алгоритма изменяются согласно следующим правилам:

в - X i , если в > X i ,

в ^ 0 , в<х i ив>—Х„

в + Х i , если в <—X i ,

где р = W ( i,j ) , а X i – значения порога.

Для решения задач очистки сигнала от шума в качестве вейвлет-функции целесообразно выбирать ортогональные вейвлеты: Добеши, симлеты или койфлеты. Выбор этих вейвлетов обусловлен, во-первых, компактностью носителя и, во-вторых, максимальным уровнем реконструкции сигнала [1].

4.    Результаты

Нами были использованы 16-ти битные тестовые сигналы с частотой дискретизации 16 кГц. На рис. 1 представлены исходный и очищенный сигналы фразы «исходный сигнал».

Для анализа эффективности очистки сигнала от шума используется следующее выражение:

N -1    ²

ZI Х.|

SNR (дБ) = ^Т=0------.       (9)

Е I xn " xn |2 n=0

Наш алгоритм использует исходную популяцию из 70 особей, достаточную для сходимости алгоритма и оптимальную с точки зрения практической реализации. В качестве вейвлет-функций были использованы симлеты 4-го порядка (Sym4) и вейвлеты Добеши (Db10).

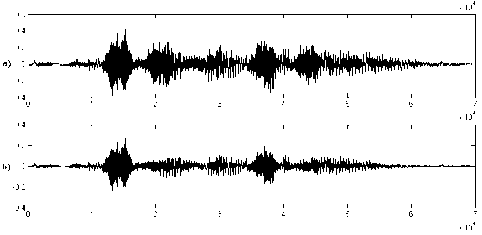
Рис. 1. Фраза «исходный сигнал»: а – зашумленный сигнал, б – очищенный сигнал

Результаты экспериментов сведены в таблицу 1. Уровень «сигнал-шум» для порогового метода выше, чем аналогичный показатель метода VisuShrink.

Таблица 1. Результаты очистки сигнала от шума

Метод	Вейвлет	SNR, дБ
VisuShrink	Db8	21,378
ПШП-ГА	Sym4 Db10	22,567 23,010

На основе полученных результатов можно сделать вывод об эффективности метода порогового шумоподавления с использованием генетических алгоритмов для подбора и оптимизации параметров преобразований.

5.    Заключение

Проведенные эксперименты подтвердили эффективность метода пороговой очистки сигнала от шума с помощью вейвлет-преобразования и генетических алгоритмов. К сожалению, использование генетических алгоритмов приводит к существенным вычислительным затратам, поэтому дальнейшие улучшения метода могут быть связаны как с оптимизацией аппарата генетических алгоритмов, так и с использованием вейвлет-деревьев.