Метод повышения точности и сокращения времени измерения частоты периодических сигналов для систем управления технологическими процессами

произвольный (в общем случае) угол Δα [5]. Однако при реализации данных методов используются мгновенные значения как входных, так и дополнительных сигналов, что неизбежно приводит к погрешности по напряжению (погрешности по модулю ФБ) [6]. Амплитуда входного сигнала может отличаться от амплитудного значения сигнала на выходе ФБ.

Исключение погрешности по модулю фазосдвигающих блоков обеспечивает метод [7]. Метод заключается в формировании двух дополнительных сигналов напряжения, сдвинутых по фазе на углы Δ α и 2Δ α относительно входного. В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на 2Δ α , измеряют первые мгновенные значения входного и дополнительного сигнала, сдвинутого относительно входного на угол Δ α . В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на Δ α , измеряют второе мгновенное значение входного напряжения. Через образцовый интервал времени Δ t с момента первого перехода через ноль одновременно измеряют мгновенные значения входного и дополнительного сигнала, сдвинутого относительно входного на Δ α . Частоту определяют по измеренным мгновенным значениям напряжения с учетом вычисленного корректирующего коэффициента, определяющего соотношение между амплитудными значениями входного и дополнительного сигналов. Недостатком метода является необходимость дополнительной коррекции по модулю, что затрудняет его реализацию.

Этот недостаток устраняется в методе [8], который также основан на формировании двух дополнительных сигналов напряжения, сдвинутых по фазе на углы Δ α и 2Δ α относительно входного, и измерении мгновенных значений только входного напряжения. В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на 2Δ α , измеряют первое мгновенное значение входного сигнала. Через образцовый интервал времени Δ t измеряют второе мгновенное значение входного напряжения. В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на Δ α , измеряют третье мгновенное значение входного сигнала. Через образцовый интервал времени Δ t измеряют четвертое мгновенное значение входного напряжения.

Частоту определяют по измеренным мгновенным значениям входного напряжения. Однако использование двух образцовых интервалов времени значительно увеличивает время измерения.

Известный метод [9] также исключает погрешность по модулю ФСБ и использует только один образцовый интервал времени A t . Метод заключается в формировании двух дополнительных сигналов напряжения, сдвинутых по фазе на углы A a и 2А а относительно входного, и измерении мгновенных значений только входного напряжения. В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на 2А а , измеряют первое мгновенное значение входного сигнала. В момент перехода через ноль дополнительного напряжения, сдвинутого относительно входного на А а , измеряют второе мгновенное значение входного сигнала. Через образцовый интервал времени A t с момента перехода через ноль входного напряжения измеряют его мгновенное значение. Частоту определяют по мгновенным значениям входного сигнала. Недостатком метода является достаточно большое время измерения, поскольку образцовый интервал времени отсчитывается с момента перехода входного напряжения через ноль.

В статье рассматривается новый метод и реализующее его средство измерения, обеспечивающие сокращение времени измерения.

Метод измерения частоты на основе использования мгновенных значений входного сигнала основан на формировании двух дополнительных сигналов напряжения, сдвинутых по фазе относительно входного соответственно на углы А а и 2А а в сторону опережения. В соответствии с методом в момент перехода второго дополнительного напряжения, сдвинутого относительно входного на 2А а , измеряют первое мгновенное значение входного напряжения. В момент перехода первого дополнительного напряжения, сдвинутого относительно входного на А а , измеряют второе мгновенное значение входного напряжения. Через образцовый интервал времени A t с момента перехода второго дополнительного напряжения через ноль измеряют третье мгновенное значение входного сигнала. Частоту определяют по измеренным мгновенным значениям. Временные диаграммы, поясняющие метод, представлены на рис. 1.

U_x = U_{m s}m ( - 2 A_a ) . В момент времени t ₂, когда первый дополнительный сигнал переходит через ноль, мгновенное значение входного сигнала примет вид U₂ = U„ sin ( -Aa ) .Через образцовый интервал времени A t после первого перехода второго дополнительного сиг-

нала через ноль (момент времени t ) мгновенное значение входного напряжения будет равно U₃ = U _m sin ( mA t -Aa ) . Используя мгновенные значе

ния напряжения, можно определить частоту сигнала:

f =

1 arcsin

2 nA t

4 U 2 - U 1

4 U ⁴

( u 3 ( и 2 -2 U 2 ) -

I U JV 4 U 4 — U 22 ( 4 U 2 - U 2 )

Анализ выражения (1) показывает, что частота сигнала не зависит от величины угла сдвига фазы A a . На рис. 2 представлена схема средства измерения (СИ), реализующего данный метод.

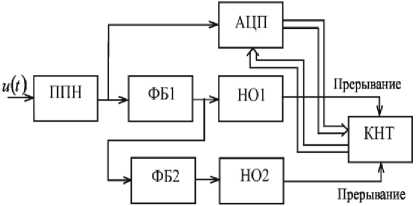
Рис. 2. Средства измерения, реализующие метод

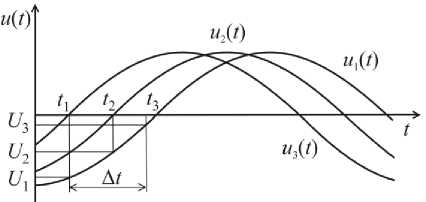
Рис. 1. Временные диаграммы, поясняющие метод

Для входного гармонического напряжения и, (t) = U sin rot дополнительные сигналы имеют вид: 1m и 2 (t ) = Um sin(rot + Aa), u3(t)= U„ sin(mt + 2Aa), где U m - амплитудное значение напряжения; и - угловая частота. В момент перехода второго дополнительного напряжения через ноль (момент времени t ), мгновенное значение входного напряжения будет равно

В состав СИ входят: первичный преобразователь напряжения ППН, два фазосдвигающих блока ФБ1 и ФБ2, имеющих одинаковые углы сдвига фазы A a , два нуль-органа НО1 и НО2, аналого-цифровой преобразователь АЦП, контроллер КНТ. Разработанный метод предусматривает измерение частоты гармонических сигналов. Если реальные сигналы отличаются от гармонической модели, то неизбежно возникают погрешности.

Анализ погрешности метода измерения частоты из-за отклонения реального сигнала от гармонической модели. Проведем анализ погрешности из-за отклонения реального сигнала от гармонической модели, используя методику, предложенную в [1]. Методика заключается в оценке погрешности результата измерения частоты, как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению модели от реального сигнала. Погрешность вычисления значения какой-либо функции, аргументы которой заданы приближенно, может быть оценена с помощью дифференциала этой функции. Погрешности функции соответствует ее возможное приращение, которое она может получить, если аргументам дать приращения, равные их погрешностям. Если в качестве аргументов использовать наибольшие отклонения реального сигнала от гармонической модели, то предельная абсолютная погрешность определения частоты сигнала примет вид:

A f =

d f d U

+

d f

d U₂

+

d f

d U₃

A U max ,

ад где AUmax = UmiiZhi - максимальное отклонение сигнала от гармонической модели; Um 1 - амплитудное значение первой гармоники напряжения; Umk – амплитудное значение k-ой гармоники напряжения; hi = Umk- - коэффициент k-ой гармоники напряжения.

В соответствии с (1) и (2) относительная погрешность определения частоты сигнала будет равна:

ад

Z hi

• 5,    =------i------------- k r²-------;-------------л X

2 wA t |cos wA t sin³ Aa cos ( mA t - 2 Aa )

x {2|cos mA t (sin mA t + sin3 Aa|)+ sin Aa x x [sin(mA t - 2Aa)sin(mAt - 4 Aa) -

• - cos ( 2юA t - 4 Aa ) ] +

+ cos ( wA t - 2Aa ) sin ( mA t + Aa ) } .              ⁽³⁾

В этом случае выражение для определения частоты в соответствии с (1) будет равно:

f =-----arcsin

2nA t

4U 2 - U '²

4 U ⁴

[ u ‘ ( U '²

-

^{2 U} 22 )

-

- U 'I V4 U 4 - U 32 ( 4 U 2 - U '² ) ] .

На рис. 4 приведены графики зависимости относительной погрешности измерения частоты от Δ α и wA t для угла Ap=0,05° при использовании выражений (1) и (4). Анализ рис. 4 показывает, что погрешность определения частоты, обусловленная различием углов сдвига фаз ФБ, в значительно большей степени от Δ α . Меньшие значения погрешность принимает при угле Δ α =30÷90º.

Анализ выражения (3) показывает, что погрешность определения частоты зависит от гармонического состава сигнала, соотношения между длительностью образцового интервала времени A t и периода сигнала и угла сдвига фазы ФБ Aa. На рис. 3 представлены графики зависимости погрешности определения частоты от m A t и Aa при наличие в сигнале первой и третьей гармоники с h = 0,1%. Разрывы графиков на рис. 3 обусловлены значениями ω Δ t и Δ α , при которых знаменатель в выражении (3) обращается в ноль. Анализ рис. 3 показывает, что при любом соотношении между длительностью образцового интервала времени A t и периода сигнала погрешность принимает меньшие значения при угле сдвига фазы ФБ Aa =80^120°, что приводит к увеличению общего времени измерения.

5/[}, %

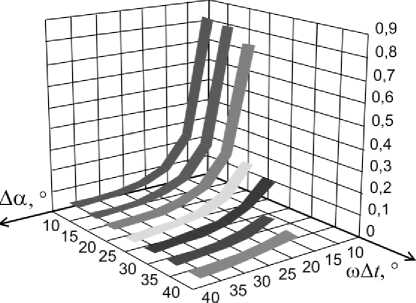
Рис. 4. Графики зависимости 5 / р от m A t и A a при Ар=0,05°

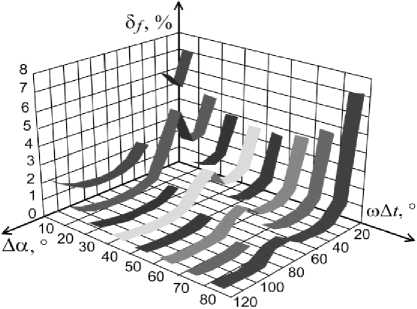
Рис. 3. Графики зависимости погрешности измерения частоты δ f от ω Δ t и Δ α

Выводы: в разработанном методе измерения частоты производится измерение мгновенных значений только входного напряжения, что исключает погрешность по модулю фазосдвигающих блоков. Использование дополнительных сигналов, сдвинутых относительно входного на произвольный угол, приводит к отсутствию частотной погрешности ФБ. Полученные результаты анализа влияния погрешностей, обусловленных отклонением реального сигнала от гармонической модели и угловой погрешности фазосдвигающего блока на погрешность результата определения частоты, позволяют выбирать оптимальные параметры измерительного процесса в зависимости от требований по точности и времени измерения.

Работа выполнена при финансовой поддержке РФФИ (грант № 16-08-00252 А)

Анализ влияния угловой погрешности формирования дополнительных сигналов на результирующую погрешность измерения частоты. Еще одним видом погрешности, который может возникнуть при реализации рассматриваемого метода, является погрешность, обусловленная не идентичностью углов сдвига фаз фазосдвигающих блоков. Если угол сдвига фазы ФБ2 будет отличаться от угла сдвига ФБ1 на Ар, то мгновенные значения входного напряжения примут вид:

U ' = U_m sin ( AP - 2 Aa ) и

U ' = U „ sin ( Ap - 2Aa + юA t ) .