Метод повышения точности планетарных передач на основе спектрального анализа экспериментальной оценки и математического моделирования кинематических погрешностей

К планетарным передачам предъявляются высокие требования точности изготовления, так как точность значительно влияет на работоспособность, надежность и ресурс работы планетарной передачи или планетарного механизма, а также на возможность сборки его деталей зацепления. В планетарных передачах и редукторах с промежуточными телами качения вращение передают сателлиты – шарики или ролики, последние могут быть цельными и сборными [1–3].

Эти передачи используются в приспособлениях для металлорежущих станков, в подъемно-транспортных механизмах, механизмах автоматизированного производства. Часто они бывают более эффективны, чем зубчатые передачи, так как при возможных больших передаточных отношениях имеют более технологичную конструкцию и меньшую стоимость.

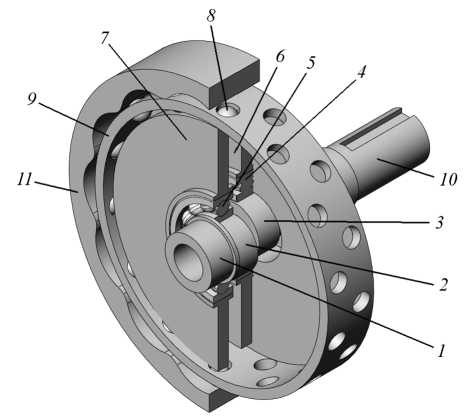
На рисунке 1 представлена планетарная передача с шариковым зацеплением.

Передача состоит из ведущего вала 1, эксцентриков 2 и 3, установленных на ведущем валу, подшипников 4 и 5, установленных на эксцентрики, ведущих дисков 6 и 7, наружные цилиндрические поверхности которых образуют ведущую беговую дорожку. Промежуточные тела качения шарики 8 являются сателлитами.Они установлены в два ряда в отверстиях водила 9, связанного с ведомым валом 10. Колесо 11 с многопериодной беговой дорожкой является неподвижным звеном. При вращении ведущего вала 1, а вместе с ним эксцентриков 2 и 3, подшипников 4 и 5, дисков 6 и 7 шарики 8 входят в зацепление с беговыми дорожками и отверстиями водила и передают вращение от ведущего вала к ведомому. Профиль многопериодной дорожки колеса 11 является эквидистантой периодической кривой, пописываемой математической зависимостью:

ρ₂ = AR² - A² sin² zφ + A cos zφ , (1) где ρ₂ – радиус-вектор точки периодической кривой; R – средний радиус периодической кривой; A – амплитуда (эксцентриситет) периодической кривой; z – число периодов кривой; φ – угол, задаваемый между точками периодической кривой.

Передаточное отношение i передачи определяется по формуле:

• 1    – ведущий вал; 2 и 3 – эксцентрик;

• 4    и 5 – подшипник; 6 и 7 – ведущий диск;

8 – сателлиты; 9 – водила; 10 – ведомый вал;

11 – колесо

• 1    – drive shaft; 2 and 3 – eccentric;

• 4 and 5 – bearing; 6 and 7 – drive disc;

8 – satellites; 9 – drivers; 10 – driven shaft;

• 11    – the wheel

Рисунок 1 – Планетарная шариковая передачаFigure 1 – Planetary ball gear i = (z1 + z2 ) / z1, (2)

где z₁ – число периодов ведущей беговой дорожки, z₂ – число периодов неподвижной многопериодной беговой дорожки.

В представленной конструкции передачи (рис. 1) z₁ = 1 .

Такую же кинематику, как у планетарных шариковых передач, имеют планетарные передачи с роликовым зацеплением [3].

Повышение точности изготовления является наиболее важной задачей для этих передач. Известны исследования, заключающиеся в разработке метода повышения точности зубчатых передач при сборке [4]. Метод заключается в определении разности началь- ных фаз поворота шестерни и колеса, при которой суммарная кинематическая погрешность передачи достигает минимума. Реализация метода заключается в том, что кинематическая погрешность описывается гармонической функцией, при этом номера зубьев шестерни и колеса для монтажа подбираются в противофазе их первых гармоник.

В исследованиях [5] механизма с циклоидальным редуктором с телами качения повышение плавности вращения редуктора обеспечивались определением оптимальной геометрии профиля зуба компьютерным моделированием с учетом неточности его формообразования при изготовлении.

Результаты исследования точности механических передач приведены в [6].В этих исследованиях на основе гармонического анализана на базе рядов Фурье получены графики кинематических погрешностей и их амплитудных спектров механических передач. Предложены методы обработки сигналов и способы фильтрации шумов при измерениях с помощью разработанной системы контроля. Предложены методы оценки точности зубчатых и других типов передач. Показаны некоторые причины образования гармоник в спектре кинематической погрешности.

Особенностью предложенного метода повыше- ния точности передач в отличие от известных и приведенных выше методов и результатов исследований является концепция, заключающаяся в повышении точности только тех деталей, которые в наибольшей степени определяют кинематическую погрешность передачи. Поэтому для определения наиболее значимых точностных параметров исследуемых передач предложен метод, основанный на спектральном анализе, который заключается в получении экспериментальных графиков и амплитудно-частотных спектров кинематических погрешностей и определении наиболее значимых гармонических составляющих спектров с целью установления причинно-следственных связей между гармоническими составляющими с наибольшими амплитудами и точностью изготовления деталей передачи.

ОСНОВНАЯ ЧАСТЬ

Экспериментальные исследования проводились на разработанном стенде [1, 2] для испытаний механических передач под нагрузкой. На рисунке 2 представлен автоматизированный стенд, который использовался для исследования кинематической точности и плавности работы механических передач (редукторов).

• 1    – аналого-цифровой преобразователь; 2 – электродвигатель; 3 и 5 – муфта; 4 – исследуемый редуктор;

6 – электромагнитный тормоз; 7 – датчик угла поворота (энкодер)

1 – analog-to-digital converter; 2 – electric motor; 3 and 5 – coupling; 4 – gearbox under study;

6 – electromagnetic brake; 7 – rotation angle sensor (encoder)

Рисунок 2 – Автоматизированный стенд для исследования кинематической точности и плавности работы механических передач

Figure 2 – Automated stand for studying the kinematic accuracy and smoothness of mechanical transmissions

Стенд (рис. 2) состоит из исследуемого редуктора 4, ведущий вал которого соединен через муфту 3 с электродвигателем 2, а ведомый вал соединен через муфту 5 с электромагнитным тормозом 6, создающим нагружающий момент на ведомом валу редуктора. К валу электромагнитного тормоза соосно установлен датчик угла поворота (энкодер) 7, соединенный с аналого-цифровым преобразователем 1, который подключен к ПЭВМ. При вращении электродвигателя 2 без нагрузки и с нагрузкой, создаваемой электромагнитным тормозом 6, неравномерность вращения ведомого вала передачи, возникающая из-за погрешностей изготовления, упругих деформаций, динамических нагрузок, зазоров в зацеплении фиксируется датчиком угла поворота 7 и в виде импульсов (сигналов) поступает на аналого-цифровой преобразователь 1 и ПЭВМ. После математического преобразования полученных сигналов с помощью разработанного программного обеспечения определяется кинематическая погрешность редуктора F_i , которую можно представить математическими выражениями:

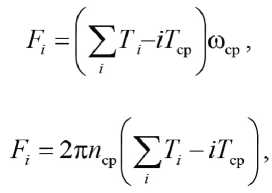
где T_i – период следования импульсов (сигналов); i – число периодов за оборот ведомого вала; T_ср – среднее число периодов; ω_ср – средняя угловая скорость ведомого вала; n_ср – средняя частота вращения ведомого вала.

В качестве примера представлены результаты экспериментальных исследований, полученные на автоматизированном стенде (рис. 2), кинематических характеристик планетарных редукторов с промежуточными телами качения с номинальной частотой вращения ведущего вала n₁ = 1500 мин^-1, изготовленных с точностью размеров наиболее ответственных деталей по 7 и 8 квалитету и с точностью их формы и расположения поверхностей, соответствующей 7 степени.

На рисунке 3 показан график кинематической погрешности F_i при числе измерений N за оборот выходного вала планетарного роликового редуктора с передаточным отношением i = 11, с числом периодов многопериодной беговой дорожки z₂ = 10, а на рисунке 4 амплитудно-частотный спектр, рассчитанный и построенный по значениям графика на рисунке 3, на котором представлены амплитуды A гармонических составляющих (гармоник) k .

На рисунках 5 и 6 показаны графики кинематической погрешности F_i планетарного шарикового редуктора с передаточным отношением i = 49 в зависимости от угла поворота ведомого вала φ₂ без нагрузки и с нагрузкой 100 Нм. Редуктор имеет две ступени. Передаточное отношение каждой ступени равно 7. Число периодов многопериодной беговой дорожки в каждой ступени редуктора z₂ = 6.

На рисунках 7 и 8 представлены графики амплитудно-частотных спектров кинематической погрешности планетарного шарикового редуктора с передаточным отношением i = 49 без нагрузки и с нагрузкой 100 Нм, на котором представлены амплитуды A гармонических составляющих (гармоник) k .

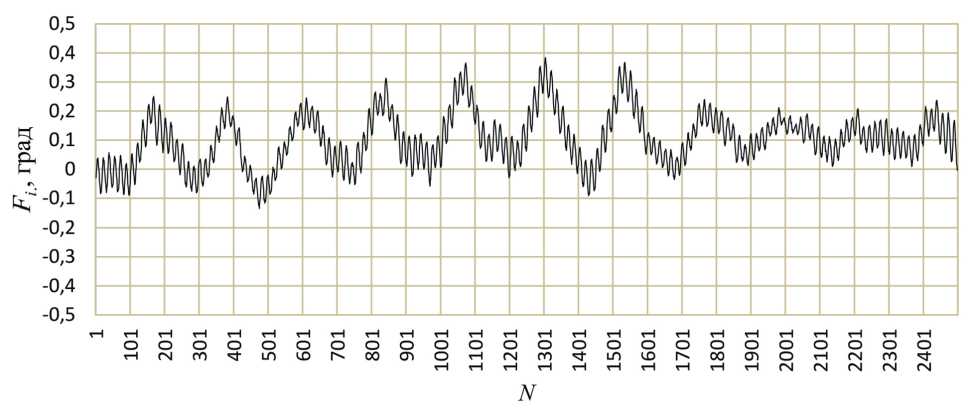
Рисунок 3 – Кинематическая погрешность планетарного роликового редуктора

Figure 3 – Kinematic error of a planetary roller gear reducer

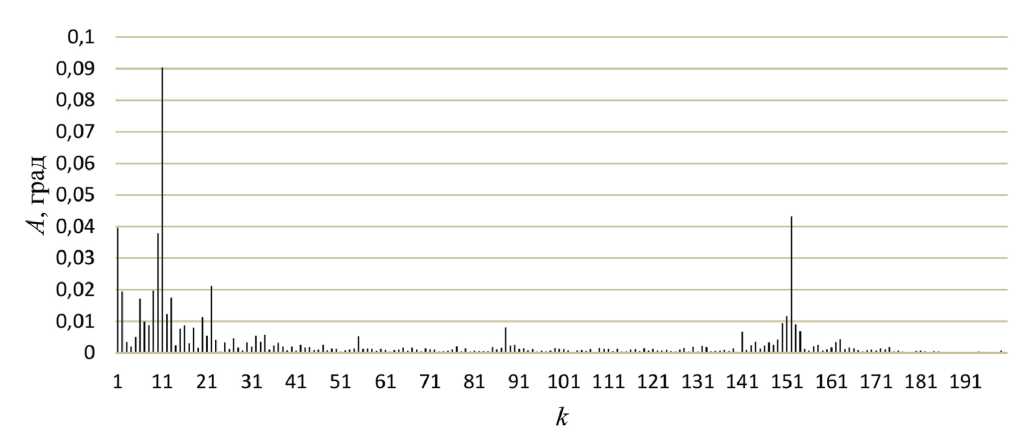
Рисунок 4 – Амплитудно-частотный спектр кинематической погрешности планетарного роликового редуктора

Figure 4 – Amplitude-frequency spectrum of the kinematic error of a planetary roller gear reducer

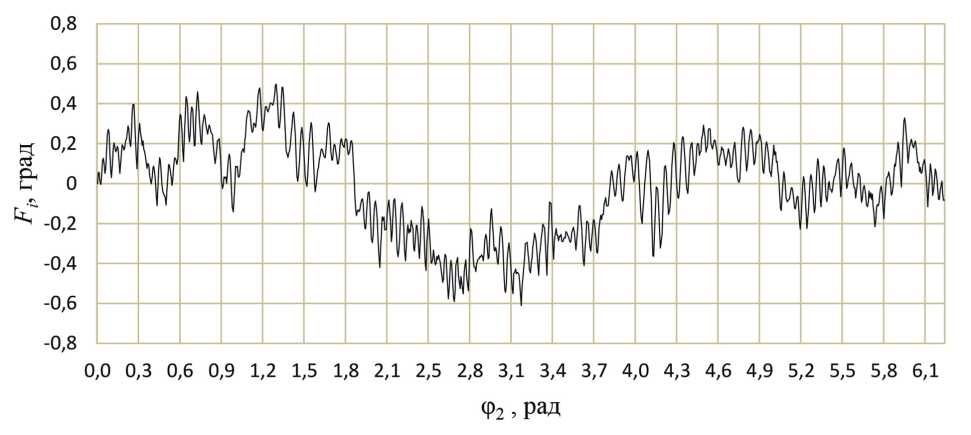
Рисунок 5 – График кинематической погрешности планетарного шарикового редуктора без нагрузки

Figure 5 – Graph of kinematic error of planetary ball gearbox without load

На графиках (рис. 3, 5 и 6) размах между наибольшим и наименьшим значением определяет наибольшую кинематическую погрешность редуктора, которая характеризует его кинематическую точность. На графике (рис. 3) выделяются волны, число которых соответствует передаточному отношению i = 11 и гармонике с номером 11 (рис. 4), а на графике (рис. 5) выделяется число волн равное 12 и кратное числу периодов беговой дорожки z₂ = 6 и гармонике с номером 12 (рис. 7), при этом величины амплитуд гармоник 11 и 12 характеризуют плавность работы редукторов.

Кинематическую погрешность передачи F(p) можно представить через гармонические составляющие ряда Фурье [1, 7, 8]:

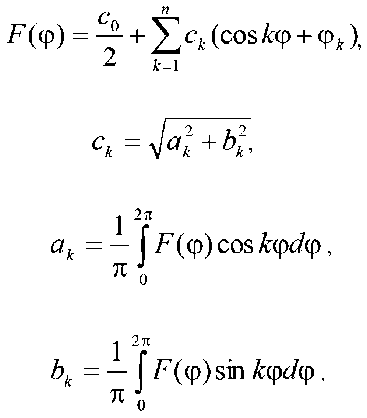
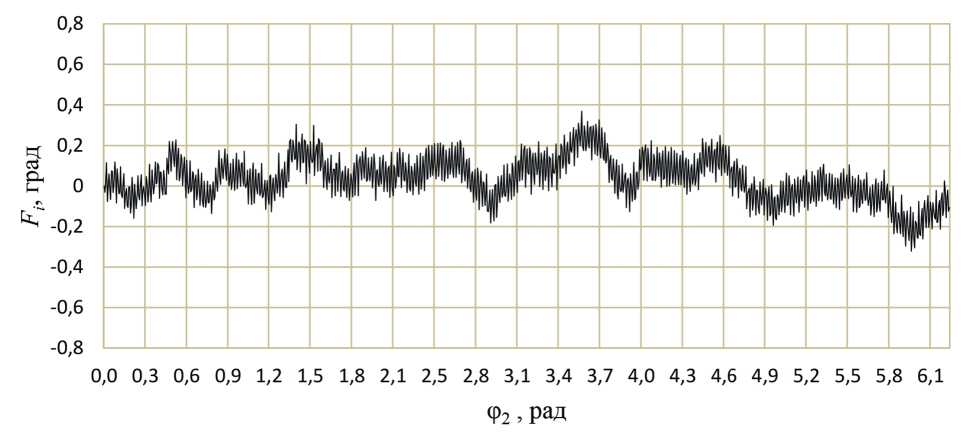
Рисунок 6 – График кинематической погрешности планетарного шарикового редуктора с нагрузкой

Figure 6 – Graph of kinematic error of planetary ball gearbox with load

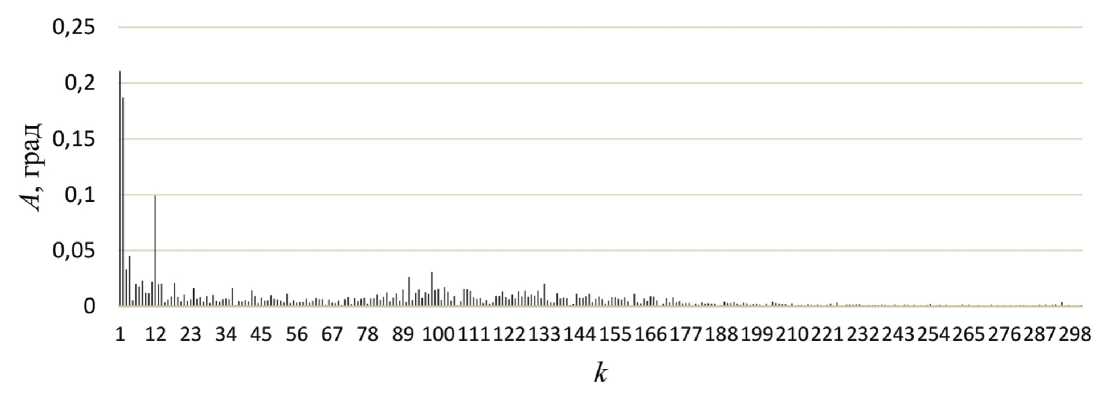
Рисунок 7 – Амплитудно-частотный спектр кинематической погрешности планетарного шарикового редуктора без нагрузки

Figure 7 – Amplitude-frequency spectrum of the kinematic error of a planetary ball gearbox without load где c0 – нулевой член и c0/2 равно среднему значению функции за период T = 2π; ck – амплитуда гармонической составляющей; ak, bk – коэффициенты ряда Фурье; k – порядковый номер гармонической составляющей; φ – угловая координата точки профиля беговой дорожки; φk – начальный фазовый угол.

По математическим зависимостям (5)…(8) можно найти амплитуды c_k гармонических составляющих и построить амплитудно-частотный спектр.

Анализ амплитудно-частотных спектров, построенных по результатам многократной экспериментальной оценки кинематических погрешностей передач, изготовленных с разной точностью деталей, позволил установить причинно-следственные связи между наиболее значимыми гармониками и погреш- ностями изготовления, которые проявляются в амплитудах этих гармоник.

Для планетарного роликового редуктора в амплитудно-частотном спектре (рис. 4) наибольшие амплитуды имеют гармонические составляющие (гармоники) с номерами 1, 10, 11, 22 и 152, а для планетарного шарикового редуктора наибольшие амплитуды имеют гармоники с номерами 1, 2, 6, 12 и 294 (рис. 7 и 8). Гармоники с номерами 1 и 2 имеют технологические причины, связанные с радиальными смещениями ведомого и неподвижного звеньев, в частности, с отклонением от соосности оси ведомого вала относительно оси многопериодной беговой дорожки при сборке. Гармоники 10, 11, 22 для планетарного роликового редуктора и 6, 12 для плане-

Рисунок 8 – Амплитудно-частотный спектр кинематической погрешности планетарного шарикового редуктора с нагрузкой

Figure 8 – Amplitude-frequency spectrum of the kinematic error of a planetary ball gearbox with load тарного шарикового редуктора соответствуют числу периодов многопериодных беговых дорожек z2 , передаточному отношению i, а также являются кратными z2 и i. Их амплитуды связаны с погрешностью шага периодов (волн) многопериодной дорожки при ее чистовой и отделочной обработке, погрешностью эксцентриситета при изготовлении ведущего эксцентрика, установленного на входном валу; смещением оси ведущего вала относительно оси многопериодной дорожки при сборке. Гармоники 152 и 294 характеризуют циклические погрешности высокой частоты. Большие амплитуды этих гармоник кратны передаточному отношению и числу периодов беговых дорожек и связаны с зазорами в зацеплении, зависящими от точности проектирования и изготовления профилей многопериодных дорожек и рабочих поверхностей водила. При больших зазорах возникает жесткий контакт при вхождении сателлитов в зацепление, что снижает плавность работы передачи.

Под нагрузкой (рис. 6 и 8) наибольшая кинематическая погрешность уменьшается за счет выборки зазоров в сопряжениях деталей и в зацеплении, а также уменьшаются амплитуды гармонических составляющих 1, 2, 6, 12 низкочастотного и среднечастотного участков спектра, но при этом значительно увеличиваются амплитуды высокочастотного участка спектра и 294-я гармоника.

Для установления влияния динамических нагрузок, упругих деформаций, неточностей проектирования профиля многопериодной дорожки, а также необходимого зазора в зацеплении проведено компьютерное моделирование планетарной шариковой передачи без погрешностей изготовления с исполь- зованием среды SolidWorks для анализа различных механизмов [9, 10]. На рисунке 9 представлено окно программы SolidWorksMotion (Анализ движения) с моделью планетарной шариковой передачи, представленной на рисунке 1. При моделировании задавались различные значения исходных параметров: задавалась частота вращения ведущего звена, нагружающий момент на ведомом звене, контакт деталей зацепления, жесткость контакта, коэффициенты трения скольжения.

В результате моделирования получены графики кинематических погрешностей при разных заданных параметрах моделирования. На рисунке 10 представлен график кинематической погрешности планетарной шариковой передачи F_i с n значениями за оборот ведомого звена, полученный моделированием с частотой вращения ведущего вала 1500 мин^-1 и нагрузкой на ведомом звене 100 Нм.

При моделировании не учитывались погрешности изготовления. Кинематическая погрешность передачи F_i в результате моделирования, представленная на графике (рис. 10) имеет размах 0,058 градуса, что составляет 8,4 % от кинематической погрешности, представленной на графике (рис. 6), полученном при экспериментальных исследованиях планетарного шарикового редуктора под нагрузкой с погрешностями изготовления. Результаты моделирования показали, что динамические нагрузки без учета погрешностей изготовления дают небольшую кинематическую погрешность планетарных передач с промежуточными телами качения и основными источниками кинематической погрешности являются погрешности изготовления, которые в динамике проявляются в высокочастотных гармониках.

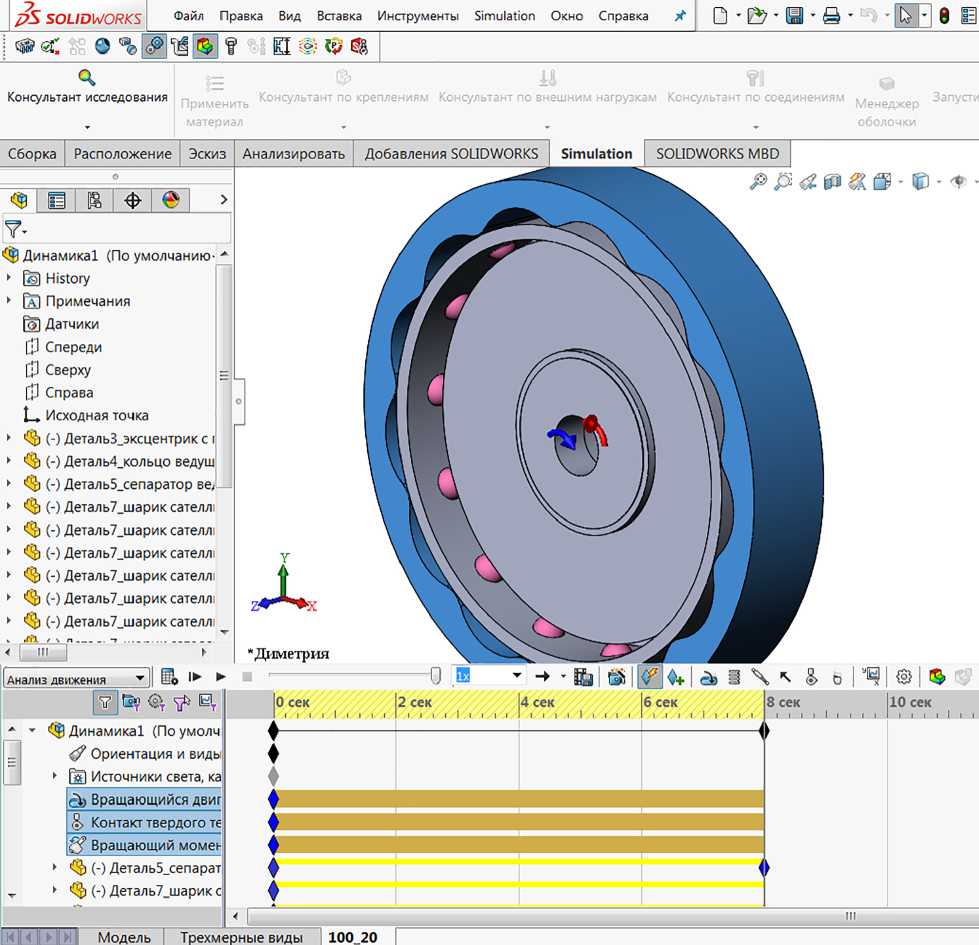
Рисунок 9 – Окно программы SolidWorksMotion с моделью планетарной шариковой передачи

Figure 9 – SolidWorksMotion program window with a model of a planetary ball gear

ЗАКЛЮЧЕНИЕ

Разработанный метод, подтвержденный результатами исследований, заключается в установлении наиболее значимых гармонических составляющих кинематической погрешности передачи, а также их связи с погрешностями изготовления. При этом повышается точность только тех деталей передачи, которые связаны с гармоническими составляющими, имеющими наибольшие амплитуды в амплитудно-частотном спектре кинематической погрешности, что позволяет повысить точность планетарных передач с промежуточными телами качения, а также уменьшить затраты на проектирование и изготовление этих передач.

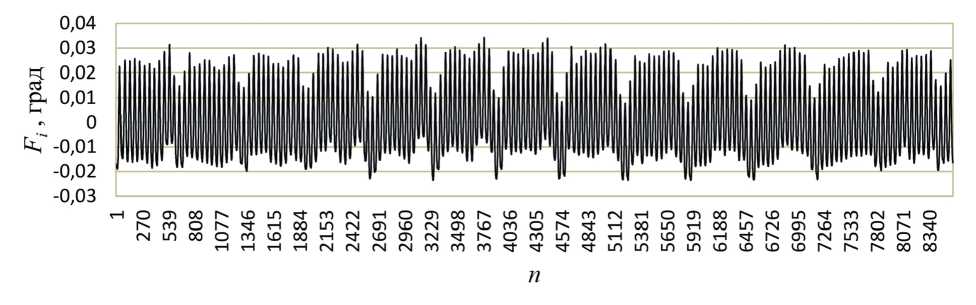
Рисунок 10 – График кинематической погрешности планетарной шариковой передачи, полученный компьютерным моделированием

Figure 10 – Graph of the kinematic error of a planetary ball gear obtained by computer modeling