Метод преобразования космических снимков, полученных при сканирующих оптико-электронных съемках

Космические изображения имеют геометрические искажения, обусловленные различными факторами, в числе которых можно выделить панорамный эффект перспективы наблюдения, кривизну поверхности Земли, эллиптичность орбиты космического аппарата (КА), рельеф местности и другие. В типовой схеме съемочной системы сканирующего типа применяется набор оптико-электронных преобразователей (ОЭП), расположенных в фокальной плоскости (ФП) телескопа с небольшим взаимным перекрытием в продольном направлении и со сдвигом друг относительно друга в поперечном направлении. Такая конфигурация набора ОЭП и законы сканирующей космической съемки приводят к тому, что каждая строка изображения характеризуется своими параметрами, поэтому формировать единое изображение из отдельных строк можно только на основе точной информации о расположении ОЭП в ФП и кинематических параметрах пространственного движения телескопа.

Совокупное действие панорамного эффекта и эллиптичности орбиты проявляется в изменении масштаба снимков, включая различную масштабность изображения по строкам. К числу основных задач геометрических преобразований изображений земной поверхности относятся трансформирование изображений в заданную картографическую проекцию; геодезическое ориентирование изображений по опорным данным; ортотрансформирование c использованием данных цифрового рельефа местности.

Представляется метод приведения космических снимков, полученных при распределенных сканирующих съемках, к единому масштабу

для последующего формирования стереоизображений или получения составного снимка из фрагментов. Метод может быть использован для обработки снимков местности, имеющих общие части и полученных различными космическими аппаратами (КА) в группировке либо одним КА в различное время, и позволяет учитывать характеристики фактического движения КА с использованием служебной информации, сопровождающей снимки. В отличие от известных стандартных подходов [1,2] к решению близких задач, предлагаемый метод не использует процедуру ортонормирования и может применяться для обработки снимков наземных местностей с небольшим перепадом высот, либо в случае, когда не предъявляются высокие требования к их измерительным свойствам.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается КА землеобзора, оснащенный телескопом с матрицами ОЭП в его ФП. При съемке поверхности Земли матрицы ОЭП работают в режиме временного запаздывания и накопления (ВЗН). Используются стандартные системы координат (СК) – инерциальная (ИСК, базис I _ф ) с началом в центре Земли O _ф , Гринвичская геодезическая (ГСК, базис E ), горизонтная (ГорСК, базис H = { h * } , рис. 1) с эллипсоидальными геодезическими координатами L , B и H , орбитальная (ОСК) и связанная с КА (ССК, базис B ) системы координат с началом в его центре масс (ЦМ) O . Вводятся также телескопная СК (ТСК, базис S = { s * } ) с началом в центре оптического проектирования S (рис. 1), СК поля изображения O ix* у* Z* (ПСК, базис F ) с началом в центре O * ФП телескопа и визирная СК

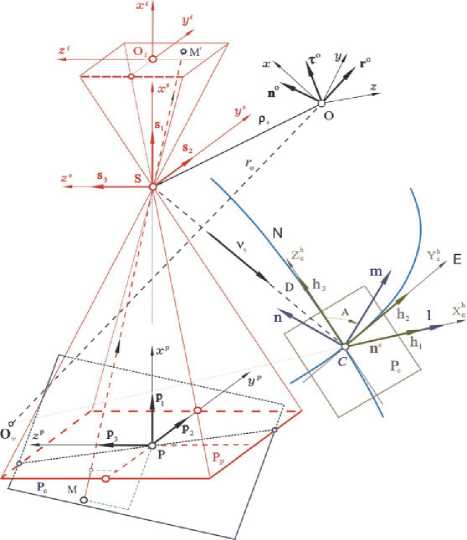
Рис. 1. Схема формирования изображения

Здесь ~ * = у * / f e и ~ * = z¹ / f e являются нормированными фокальными координатами указанной точки, где f_e – эквивалентное фокусное расстояние телескопа. Пусть далее векторы-столбцы to S и v S представляют в ТСК соответственно угловую скорость и скорость поступательного движения центра масс КА относительно ГСК. Тогда продольная V * (у‘,z * ) и поперечная V ^~ _z ( ^~ y , ^~ z ) составляющие вектора нормированной скорости движения изображения (СДИ) точки M ( у * , z ) вычисляются по вектор-

но-матричному соотношению

V (z * ,~ * )

V z (z * ,~ * ).

• ■ z *

■ ■ z

z * z *

i~x q ve1

i~x q ve 2

- y * to s 3 + z tof 2

i~x q ve1 +

x ~ i x

®e 3 ^- z to 1

x ~ i x toe2 + y toe1

. (2)

(ВСК O _v x ^v y ^v z ^v , базис V ) с началом в центре O линейки матриц ОЭП [8]. Математическое описание съемки земной поверхности содержит модели съемочной системы (v); орбитального (r) и углового ( а ) движений КА, общеземного эллипсоида (ОЗЭ) (e) и представляется в виде

А = FB⁽ x ", У \ H , P v , P r , P a , P e ) ;

L = F L⁽ x v , У \ ^H , P v , P r , P a , P e ) .

где P _v, P _r, P _a , p _e - векторные параметры соответствующих моделей. Эти соотношения используются при решении как прямой, так и обратной фотограмметрических задач.

При наличии достаточного числа реперов в получаемых изображениях можно использовать модификации известных методов масштабирования и координатной привязки видеоинформации, полученной при сканирующих съемках [4, 6]. Пусть матрица C = | ~- | определяет ориентацию ТСК относительно ГСК, а скалярная функция D( t ) представляет дальность наблюдения вдоль оси визирования с ортом v s , см- рис.1. Представление координат произвольной точки M в основной плоскости пространства предметов Р _с (рис. 1) в оптическом базисе S = { s, } и применение классических соотношений центральной проекции теории оптических систем приводит к формулам связи координат точки ^M и её отображения M ( y¹ , z ) в основной плоскости y* O . z* базиса F :

у =- y s / x^s ; ~ * =- z^s / x^s ;

x^s = - d/ q, q = 1 - (z₂₁~ * + z₃₁z * )/z_n

Пусть имеется два снимка наземной местности с частичным перекрытием, которые были получены с помощью сканирующей оптикоэлектронной съемки различными КА землеоб-зора либо одним КА в различное время, причем каждый снимок снабжен служебной сопровождающей информацией (ССИ), где имеются лишь неточные и/или редкие измерения параметров

P _r движения ЦМ КА. Рассматривается задача приведения космических снимков, полученных при таких распределенных сканирующих съемках, к единому масштабу. При этом второй снимок условно считается основным, именно в его масштаб пересчитывается масштаб первого снимка. Разработанный метод содержит четыре последовательно выполняемых этапа:

• 1.    восстановление характеристик пространственного движения КА при сканирующей съемке и получении каждого снимка, используя методы уточнения параметров p _r, p _a на основе комплексной обработки снимков совместно с ССИ [5], [7-9];

• 2.    пересчет пикселей первого снимка на поверхность ОЗЭ с применением ССИ и уточненных характеристик движения;

• 3.    пересчет сетки пикселей второго снимка на поверхность ОЗЭ;

• 4.    формирование первого снимка в масштабе второго снимка.

УТОЧНЕНИЕ ДВИЖЕНИЯ КА ПРИ СЪЕМКЕ

Поступательное и угловое движения КА уточняются по опорным объектам, выбранным на паре снимков, с использованием сведений об элементах внутреннего рv и внешнего рr, pa ориентирования съемочной аппаратуры. Уточнение движения центра масс КА выполняется с привязкой к карте GOOGLE Earth. На этой карте выбираются опорные объекты, находящиеся на поверхности со средним превышения H , с ис пользованием параметров Pv находятся соот-

ветствующие объекты на снимках и вычисляются геодезические координаты (широта B и долгота L ) их расположения на поверхности ОЗЭ. По разности координат опорных объектов на карте и полученных по результатам таких вычислений определяется средняя поправка к параметрам p _r движения ЦМ КА, оптимальная по методу наименьших квадратов.

Для уточнения углового движения КА, телескоп которого оснащен более чем одной линейкой ОЭП, эффективно применение методики [5,7]. Если же имеется лишь одна линейка матриц ОЭП с зонами перекрытия, то используется методика, основанная на последовательном уточнении значений вектора угловой скорости и кватерниона ориентации КА. Такое уточнение выполняется по информации о продольных S y и поперечных S Z сдвигах изображения на ОЭП (в плоскости y ^v O_v z ^v ВСК) с использованием метода функционализации [3]. Согласно разработанной методики [9] сначала для известных по ССИ временных интервалов сканирующей съемки выполняется перерасчет движения ЦМ КА для рассматриваемой пары снимков с вычислением соответствующих новых начальных условий. В результате получаются массивы значений радиус-векторов r*"( t_k ), k e N K . (0,1,...K) и r 02) ( t m ), m e N “ , а также скоростей поступательного движения v oⁿ ( t k ), k e N K и v 0²⁾ ( t m ), m e N ^M , центра масс КА на интервалах времени маршрутов получения первого и второго снимков, соответственно. Далее для каждого снимка определяется фактическая угловая скорость КА при сканирующей съемке. Компоненты СДИ в зонах перекрытия матриц ОЭП и сдвиги изображения связаны соотношениями

Vsv = (Sy + p) rh «-V;

,    (3)

V sz = S sz rh « V sz , s = 1 - ( n - 1) где h – частота переноса зарядов по столбцам, r – размер пикселя, p – расстояние между рядами матриц, n – число матриц в линейке ОЭП. Массив значений кватерниона ориентации КА в составе ССИ соответствующего снимка проходит компьютерную обработку с исключением некорректных данных, фильтрацией шумов измерений и далее используется для формирования массивов значений дальности D , матрицы C = | ~ j | ориентации ТСК относительно ГСК и вектора скорости v s поступательного движения ТСК относительно ГГСК по скорректированным параметрам p _r движения ЦМ КА. Для ^s -ой точки изображения первого снимка в момент времени t _k , k e N K , формула (2) представляется уравнением a s © e ( t _k ) = ь s , где искомый вектор-столбец © s ( t_k ) = { to s, ( t_k )} , а известные с учетом вычис-

лений компонентов СДИ по формуле (3) матрица

A и столбец b имеют явный вид ss

A s

b s

^^^^^^^в

~

~ ^j

~.-

~i~i ysizsi

^^^^^^^в

(1 + (~ s )²)

1 + (~ )²

. V y ( y , ^)

~ -

V Z (~ s ,~)

— q

^^^^^^^^

~i~i ysizsi

~ - ~ s

~ s

• V v,+v' ,- ys * el * t

e2

;

s

~ i r— c r— c

Z * v e s 1 ⁺ v s 3

для s = 1 - ( n - 1) . Далее набор таких n - 1 уравнений разрешается относительно вектора © ss ( t _k ) по методу наименьших квадратов, в результате получается оценка toX t _k ) = A # B . ( A ‘ A ) ^{- 1} A t B , где составные матрицы A = { A 1 , A ₂,... A _n - 1 } и B . { b 1 , b ₂,... b _n - 1 } . Расчет значений указанной оценки выполняется для моментов времени маршрута, соответствующих последовательности строк снимка, с первой строки до конечной с заданным шагом. В результате получается массив оценок вектора угловой скорости ct) s ( t _k ) , k e N K . Аналогичным способом формируется массив оценок вектора угловой скорости © e ( t m ) , m e N M при выполнении маршрута съемки, соответствующего второму снимку. Полученные оценки после фильтрации и высокоточной сплайновой аппроксимации применяются для уточнения фактической ориентации каждой строки изображения в матрицах ОЭП с помощью численного интегрирования соответствующего кватернионного уравнения. В результате выполнения данного важного этапа получаются уточненные значения положения и угловой ориентации телескопной системы координат при съемке.

ПЕРЕСЧЕТ МАСШТАБА СНИМКОВ

Схема пересчета масштабов представлена на рис. 2 а , где используются массивы информации I q и оси координат X q = y ^ , y_q = z ^v ( q = 1,2 ) снимков. По скорректированным значениям параметров p _r и p _a движения ТСКдля t = t _k каждый пиксель первого снимка ( q = 1 ) проектируется на поверхность ОЗЭ с учетом среднего превышению местности. В результате для каждого пикселя, расположенного на пересечении i- ой строки и j -го столбца первого снимка получается массив данных ( L 1 , B 1 , J 1 , r 1 ) ^ , - = 1 - n 1 , j = 1 - m 1 , где использовано обозначение яркости J ₁ пикселя этого снимка. Аналогично выполняется пересчет координат сетки пикселей второго снимка на поверхность ОЗЭ с формированием массива данных ⁽ L 2 , B 2 , ^r 2 ) j , - = 1 - n ₂, j = 1 - m ₂ , где - и j - номера строки и столбца на «заготовке» первого снимка в масштабе второго снимка. При этом ширина линейки матриц ОЭП в ФП телескопа, соответствующего второму снимку, формально может быть увеличена для захвата всей площади первого снимка.

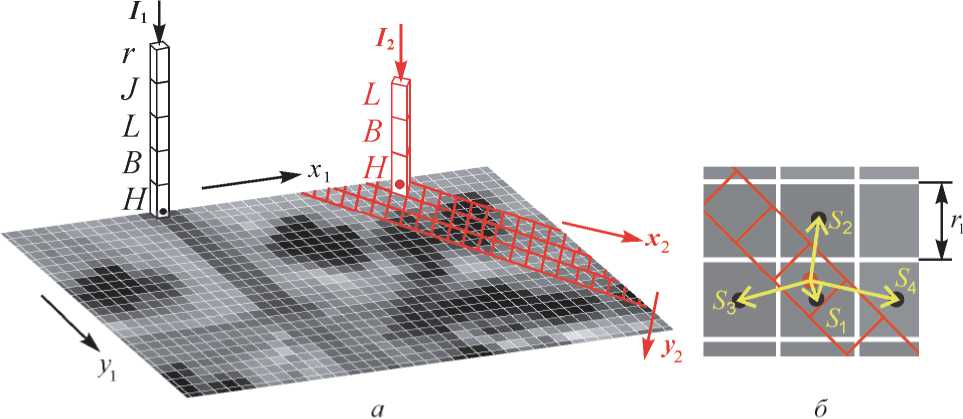
Рис. 2. Схема пересчета масштаба снимков

На завершающем этапе первый снимок формируется в масштабе второго снимка. При этом для каждого пикселя на пересечении i -ой строки и j -го столбца второго снимка устанавливается яркость J *j = Z k (1 - S k I r 1 ) J 1 _k , где J 1 k - значения яркостей ближайших пикселей первого снимка, расстояния S _k до ближайших центров которых удовлетворяют условию S k <  r 1 , см. рис. 2 б .

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

На рис. 3 представлен снимок, составленный из фрагментов, которые были получены в разное время с различными условиями по высоте полета

КА и ракурсу. На рис. 4 показан фрагмент шва этого снимка, на котором заметно, что его составные части получены при различных высотах Солнца над горизонтом, что отражается в различных направлениях тени. Указанные исходные снимки были сформированы в различное время с различных высот полета КА ( h 1 = 464 км, h 2 = 368 км) и при различных углах крена ( у 1 = - 3 o , у 2 =+ 10 o ) трассовой сканирующей съемки

ЗАКЛЮЧЕНИЕ

Предложен метод приведения космических снимков, полученных при распределенных сканирующих съемках, к единому масштабу. Данный

Рис. 3. Пример составного снимка

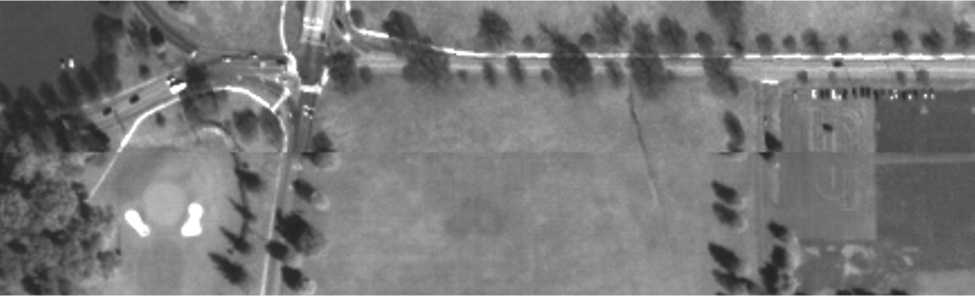
Рис. 4. Фрагмент шва составного снимка

метод не использует процедуру ортонормирования и может применяться для обработки снимков наземных местностей с небольшим перепадом высот, либо в случае, когда не предъявляются высокие требования к их измерительным свойствам. Представлены численные результаты, демонстрирующие работоспособность предложенного метода преобразования масштабов.