Метод прямого статистического моделирования в задаче Томсона

Математически эта задача сводится к поиску величины

W„ =     inf     W ( y ⁽¹⁾,..., y (N) ),

N y ⁽¹ ) ,..., y ( N ) e S ²

N

W ( y ⁽¹⁾,..., y ⁽ N) ) = У       ¹ ,, .

,              ^ il y ⁽⁰ - y⁽ jj

* j

Еще сам Томсон проводил физические эксперименты по нахождению таких конфигураций для небольшого количества зарядов. Решающее значение для решения этой задачи уже в середине XX в. имела теория приближения функций П. Л. Чебышева, на основе которой частные случаи (при N = 2, 3, 4, 6, 12) были исследованы аналитически. Соответствующие конфигурации приведены в таблице на светло-сером фоне.

Дальнейшие исследования привели лишь к частичным результатам для случая N = 120 в 4-мерном пространстве (заряды составляют правильный многогранник, имеющий соответствующее число вершин) и N = 196 560 в 24-мерном пространстве (заряды расположены на концах минимальных векторов решетки Лича).

Также существуют конфигурации, полученные экспериментальным путем, но не доказанные математически (они выделены в таблице темным фоном).

В данной статье для решения задачи Томсона использовался метод прямого статистического модели-

рования. Была разработана компьютерная модель, основанная на кинематике движения зарядов по поверхности сферы и их взаимодействия между собой.

Первая реализация модели выполнена в среде Borland C++ Builder. Она проводила итеративный поиск решения задачи Томсона для заданного количества зарядов. За каждую итерацию рассчитывались силы взаимодействия зарядов друг с другом, и на основе их результирующей выполнялся одновременный пропорциональный сдвиг зарядов. Благодаря классам визуализации и системе отображения результатов математически доказанные случаи были подтверждены экспериментально.

Следующая реализация модели разработана в среде Visual Studio с применением библиотек MPI в связи с необходимостью статистического исследования полученных конфигураций. Это существенно увеличило производительность моделирования за счет использования распределенных по локальной сети вычислений.

Таким образом, для каждого числа N генерируется 500 000 случайных начальных конфигураций на сфере и для каждой такой конфигурации рассчитывается около 100 000 итераций по времени. Такой подход позволяет с высокой вероятностью сделать заключение о минимальности потенциальной энергии той или иной системы зарядов, а также найти равновесные конфигурации (рис. 1–8).

Исследования разработанной модели позволили найти ряд неизвестных конфигураций в задаче Томсона. Результаты компьютерного моделирования некоторых систем зарядов получены впервые и приведены в таблице на белом фоне.

Исследованные конфигурации систем зарядов

Число зарядов	Потенциальная энергия	Характеристика конфигурации
2	1	Полюса сферы
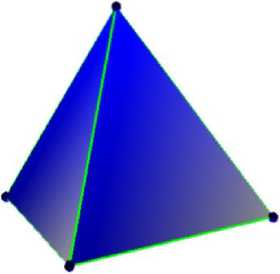
3	2√3	Правильный треугольник на экваторе
4	3√6	Правильный тетраэдр
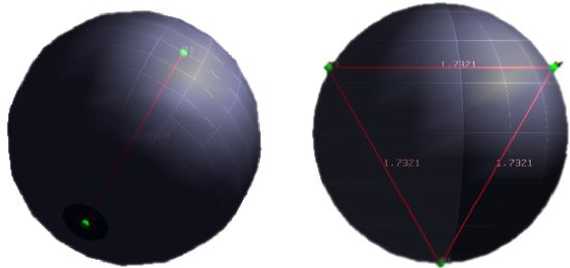
5	12,949 381 8	Два заряда на полюсах, три заряда образуют правильный треугольник на экваторе
5	12,967	Правильная пирамида
6	3 + 12√2	Правильный октаэдр
7	28,905 956 3	Два заряда на полюсах, пять зарядов образуют правильный пятиугольник на экваторе
8	39,350 574 5	Антипризма
9	51,520	Заряды образуют три пирамиды с прямоугольниками в основаниях, которые в свою очередь образуют друг с другом правильную треугольную призму

*Работа поддержана Российским фондом фундаментальных исследований (грант № 08-01-00312).

Окончание таблицы

Число зарядов	Потенциальная энергия	Характеристика конфигурации
10	65,433 899 0	Два заряда на полюсах, остальные заряды образуют антипризму, равноудаленную основаниями от полюсов
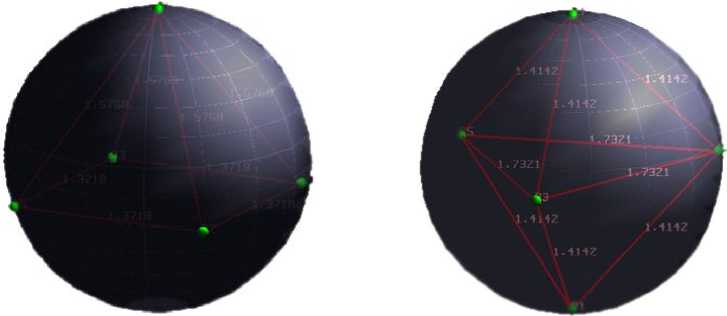
11	81,192 901 6	Конфигурация, как в предыдущем случае, отличающаяся только асимметрией за счет добавления одиннадцатого заряда между основанием антипризмы и зарядом на одном из полюсов
12	6 + 15√(10 – 2√5) +15√(10 + 2√5)	Правильный икосаэдр
13	117,706	Предположительно деформированный икосаэдр
14	138,612 686 2	Два заряда на полюсах, остальные образуют шестиугольную антипризму с основаниями, равноудаленными от полюсов
15	161,340 484 6	Конфигурация, как в предыдущем случае, но деформированная за счет пятнадцатого заряда, разместившегося рядом с одним из полюсов
16	185,823	Предположительно деформированная двумя зарядами конфигурация N = 14
16	185,841	Равновесная конфигурация с антипризматическими основаниями северного и южного полюсов
17	212,101	Конфигурация, образованная двумя правильными пирамидами, с пятиугольниками в основании, вершинами на полюсах и квадратами, повернутыми на 45° и соединенными друг с другом, на экваторе
18	240,169	Антипризматически расположенные правильные пирамиды с квадратом в основании и одинаково ориентированные пирамиды с неправильными одинаковыми прямоугольниками в основании на экваторе
19	270,179	Правильная пирамида с правильным шестиугольником в основании, расположенная на одном полюсе параллельно квадрату на другом
20	301,763	Более устойчивая, чем додекаэдр, конфигурация

N = 4

N = 2

N = 3

Рис. 1

N = 5 (равновесная конфигурация)

N = 5 (конфигурация с минимальной энергией)

Рис. 2

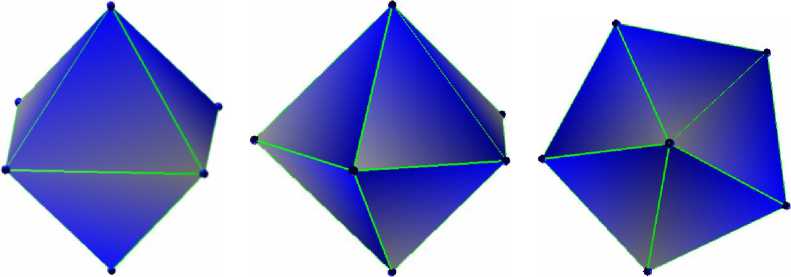
N = 6

N = 7 (вид сверху)

N = 7

Рис. 3

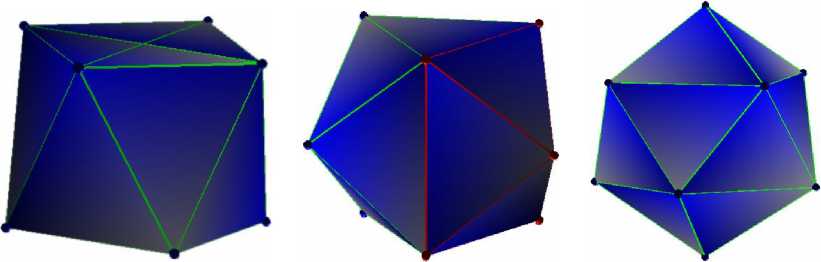
N = 8                              N = 9                          N = 10

Рис. 4

N = 11                               N = 12                          N = 13

Рис. 5

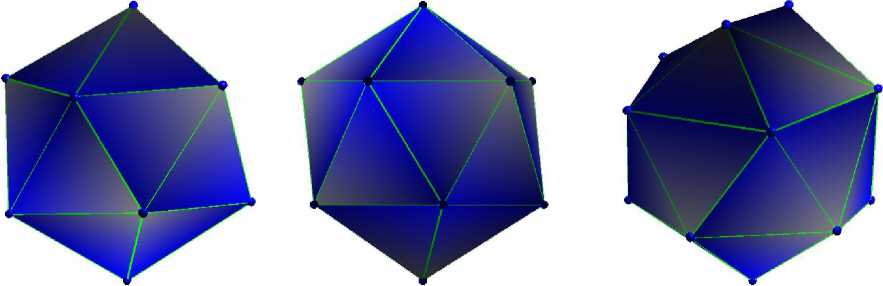
N = 14

N = 15

N = 14 (вид сверху) Рис. 6

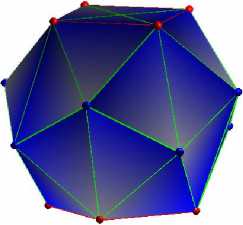
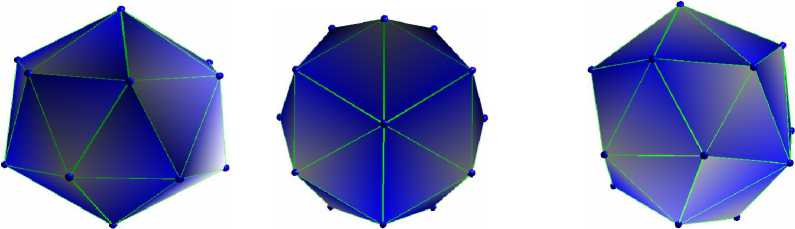
N = 16 (равновесная конфигурация)

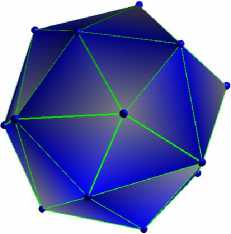
N = 16 (минимальная конфигурация)

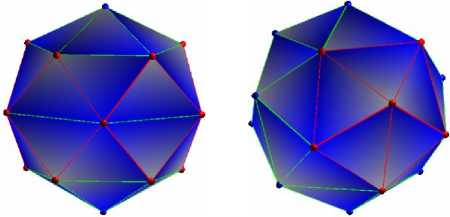
N = 17                       N = 18

Рис. 7

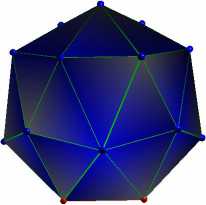
N = 19

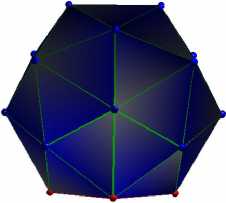
N = 20

Рис. 8

Таким образом, были исследованы системы зарядов, обладающие минимальной потенциальной энергией. Большой интерес также представляют равновес-

ные конфигурации, являющиеся локальными минимумами, а также вероятности распределения зарядов в той или иной конфигурации.

DIRECT STATISTICAL SIMULATION METHOD IN THOMSON’S PROBLEM

In the article the author presents results of search of minimal and stable arrangements of points on a sphere with the help of Monte Carlo method. Analysis of new arrangements is carried out.