Метод прямой переменнотоковой кулонометрии с расчетом полного количества электричества по величине кулонометрической константы. Определение хинона и гидрохинона

Потенциостатическая кулонометрия (ПК) является одним из самых точных методов анализа, что обуславливает ее применение в пробирном анализе и при аттестации стандартных образцов. Недостатком потенциостатической кулонометрии в ее классическом варианте является длительность измерений и невысокая чувствительность

Существует несколько способов нахождения полного количества электричества. Один из них предложил Мейтс [1]. В этом варианте метода необходимо проводить три последовательных измерения количества электричества Qt с различными временами накопления tн, удовлетворяющими условию (A12 -At1) = (A13 -A12). Полное количество электричества Q∞ рассчитывается по формуле i0

Q ^      ,

k

которое позволяет рассчитать Q ∞ из результатов амперометрических измерений при условии, что известна величина k . Значение последней определяется условиями проведения измерений и теоретически может быть найдено по уравнению

, D • S k =----- ,

5 • V

где S — площадь поверхности рабочего электрода; D — коэффициент диффузии; V — объем раствора и δ — толщина диффузионного слоя.

Экспериментально кулонометрическая константа k может быть найдена по уравнению

Q „ =

Q 2 — Q i Q 3

2 Q 2 - ( Q i + Q 3 ).

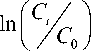
- kt .

Недостатком метода является необходимость проведения трех последовательных измерений, что увеличивает время анализа.

В работах [2, 3] предложено рассчитывать полное количество электричества по формуле

Или переходя к десятичным логарифмам:

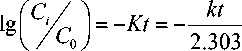
Q „ =

Q t

1 - e ^- kt '

Этот способ также не лишен недостатков: например, необходимости интегрирования тока по времени. При этом из теории кулонометрии известно, что количество электричества Q ∞ , необходимое для электропревращения вещества, связано с начальным током i⁰ и кулонометрической константой k следующим выражением:

где С i — текущее значение концентрации в любой момент времени, С 0 — начальная концентрация (коэффициент K далее будем также именовать кулонометрической константой).

Известно, что зависимость предельного тока от концентрации является линейной с коэффициентом пропорциональности k’ i0 = k' C. (7)

Концентрационная константа связана с кулонометрической следующим [4] выражением:

k ' = n F kV ,                    (8)

где F — постоянная Фарадея (F = 96500 Кл∙моль).

Настоящая работа посвящена разработке переменнотокового варианта прямой потенциостатиче-ской кулонометрии. В качестве объекта исследования выбрана электрохимически обратимая, хорошо изученная [5–8] система хинон—гидрохинон.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Измерения проводили в переменнотоковом, постояннотоковом и импульсном режимах. Переменнотоковый вариант был реализован на вольтамперометрическом анализаторе АКВ-07 с трехэлектродным датчиком. При работе в постояннотоковом и импульсном режимах анализатор был подключен к полярографу ПУ-2. Данные записывали на ПЭВМ через интерфейсный блок "Графит-2". В качестве фонового электролита был выбран фосфатный буферный раствор с pH = 7. В качестве рабочих электродов использовали золотые вращающиеся дисковые электроды с площадью рабочей поверхности S эл .= 0.071 см². Электрод сравнения — хлоридсеребряный ( Е = 0.203 ± 0.001 В); вспомогательный — стеклоуглеродный тигель, служащий одновременно измерительной ячейкой. Скорость вращения рабочего электрода составляла во время анализа 1000 об./мин. Ячейки малого объема изготавливали аналогично [2]. Перед работой через ячейку в течение 15 мин продували аргон для удаления растворенного кислорода.

Очистка хинона проводилась перегонкой с паром, гидрохинон использовался без предварительной очистки. Растворы хинона и гидрохинона с концентрацией 1·10–2 М готовились по точной навеске.

Обработку экспериментальных данных проводили с помощью программ Grafit-2 и Origin 6.1

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Для нахождения кулонометрической константы электрохимической ячейки проводили электролиз растворов с известной концентрацией гидрохинона. Кулонометрическую константу K находили из графика зависимости –lg( C i / C 0 ) от времени электролиза для каждого объема V i . Как следует из формулы (4), величина константы является функцией объема анализируемого раствора. На рис. 1 представлены зависимости –lg( C i / C 0 ) гидрохинона от времени электролиза для объемов раствора 2, 3, 4, 5 мл. Для каждого из них были рассчитаны значения констант. Аналогичные измерения были проведены для хинона (рис. 2). Результаты измерений приведены в табл. 1. Из данных, представленных в табл. 1, следует, что среднее значение константы K , приведенное к объему, равному 1 мл, является величиной постоянной, равной при данных условиях измерений — для гидрохинона K ср = = 2.60∙10^–3 мл/с, для хинона K ср = 3.32∙10^–3 мл/с. Величины значений констант k , согласно (6), составили 6.01∙10^–3 и 7.64∙10^–3 мл/с соответственно.

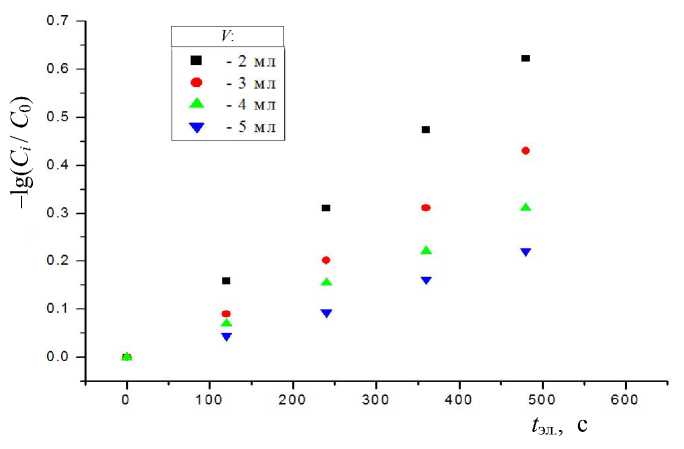
Рис. 1. Зависимости –lg( C i / C 0 ) гидрохинона от суммарного времени электролиза t эл. для различных объемов V = 2–5 мл.

S эл-да = 7.1 мм², С х = 5∙10^-4 M

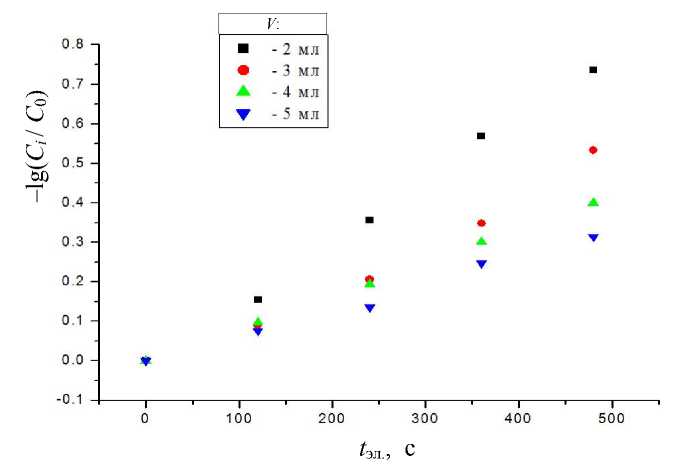
Рис. 2. Зависимости –lg( C i / C 0 ) хинона от суммарного времени электролиза t эл. для различных объемов V = 2–5 мл.

S эл-да = 7.1 мм², С х = 5∙10^-4 M

Табл. 1. Значения кулонометрических констант хинона и гидрохинона, определенных для различных объемов

Гидрохинон				Хинон
V ячейки, мл	K	K∙V	k∙V	V ячейки, мл	K	K∙V	k∙V
2	1.3∙10–3	2.60∙10–3	5.99∙10–3	2	1.59∙10–3	3.18∙10–3	7.32∙10–3
3	8.9∙10–4 8.8∙10–4 9.1∙10–4	2.67∙10–3 2.64∙10–3 2.73∙10–3	6.15∙10–3 6.08∙10–3 6.28∙10–3	3	1.14∙10–3	3.42∙10–3	7.88∙10–3
4	6.5∙10–4	2.60∙10–3	5.99∙10–3	4	8.3∙10–4	3.33∙10–3	7.67∙10–3
5	2.55∙10–4	2.55∙10–3	5.87∙10–3	5	6.7∙10–4	3.33∙10–3	7.67∙10–3
Среднее значение		2.61∙10–3	6.01∙10–3	Среднее значение		3.32∙10–3	7.64∙10–3

В соответствии с уравнением (5) величина K не должна зависеть от начальной концентрации раствора С 0 . Для проверки соответствия экспериментальных данных указанному уравнению были определены кулонометрические константы для растворов с различными концентрациями гидрохинона в растворе. Полученные данные свидетельствуют о том, что значения констант практически не зависят от концентрации гидрохинона в растворе в изученном диапазоне концентраций (см. табл. 1).

Из уравнения (4) следует, что величина кулонометрической константы обратно пропорциональна объему исследуемого раствора. Экспериментальным подтверждением этому являются приведенные на рис. 3 для гидрохинона и на рис. 4 для хинона зависимости lg ( C i / C 0 ) от –1/ V при различных временах накопления, которые представляют собой прямые линии, сходящиеся в одной точке при достаточно больших объемах раствора, когда практически не происходит изменения концентрации при электролизе.

Переменнотоковая вольтамперометрия является существенно более чувствительным методом, чем постояннотоковый вариант за счет применения фазовой селекции тока. Однако применение переменнотоковой развертки потенциала осложнено тем, что при регистрации переменнотоковых вольтамперограмм происходит дифференцирование тока по потенциалу. Это осложняет нахождение абсолютного значения величины предельного диффузионного тока, ввиду того что константа интегрирования (т. е. обратной операции), как правило, неизвестна и является величиной, характеризующей определенный прибор. Для поляро-графа ПУ-2 эта проблема была решена аналогично [9] путем нахождения коэффициента высот пиков в переменнотоковом режиме на значение предельного тока. С этой целью были получены зависимости величин пиков от концентрации гидрохинона в переменнотоковом (отн. ед.) и постояннотоковом (А) режимах. Данные представлены на рис. 5 и 6 соответственно. Как следует из этих tэл.:

0.05

0.00

-0.05

О’ -0.10

"^ -0.15

-0.20 ею "7 -0.25

-0.30

-0.35

-0.40

-0.45

-0.50

-0.55

-0.60

-0.65

- 240

- 360

- 480

С

с

с

Рис. 3. Зависимости значений –lg( C i / C 0 ), нормированных по времени, от –1/ V для гидрохинона, построенные по данным, приведенным на рис. 1, для времен электролиза 240, 360, 480 с

—I-----------1-----------1-----------1-----------1-----------1-----------1-----------1-----------1-----------1-----------Г"

-0.5         -0.4         -0.3         -0.2         -0.1          0.0

– 1 / V (мл)

0.05

0.00

-0.05

-0.10

-0.15

-0.20

-0.25

-0.30

-0.35

-0.40

-0.45

-0.50

-0.55

-0.60

-0.65

-0.70

-0.75

-0.80

- 240

- 360

- 480

Рис. 4. Зависимости значений –lg( C i / C 0 ), нормированных по времени, от –1/ V для хинона, построенные по данным, приведенным на рис. 2, для времен электролиза 240, 360, 480 с

—1---------1---------1---------1---------1---------1---------Г”

-0.5         -0.4         -0.3         -0.2

—1-----1-----Г

-0.1          0.0

– 1 / V (мл)

данных, обе зависимости представляют собой прямые в широком диапазоне концентраций. Среднее значение коэффициента пересчета составило (3.1±0.1)∙10–6 А/отн. ед.

Концентрационная константа k’, рассчитанная из данных, представленных на рис. 6, составила 1170 А·см3/моль. Подставляя полученное значение в уравнение (8), получаем значение константы, приведенной к объему 1 мл, kV = 6.1∙10–3 с–1·мл, что хорошо согласуется с величиной константы, полученной из данных, представленных на рис. 1. Следовательно, найденные значения кулонометрических констант могут быть использованы при определении концентрации гидрохинона и хинона в растворе. Проверка последнего утверждения была выполнена с использованием метода "введено-найдено". Результаты анализа образцов с различной концентрацией исследуемого раствора приведены в табл. 2.

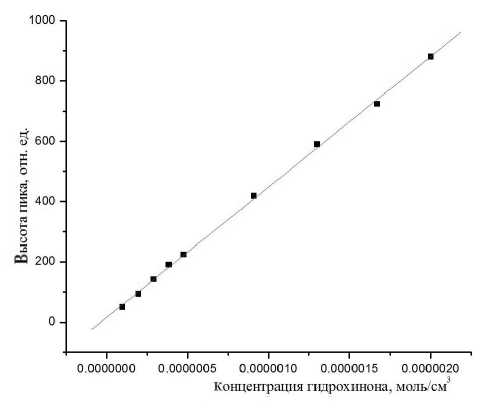
Рис. 5. Зависимость высоты пика гидрохинона от его

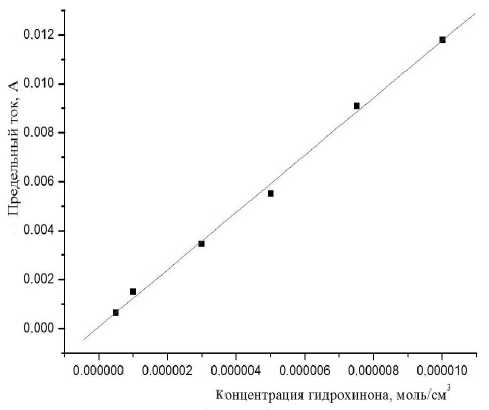
Рис. 6. Зависимость величины предельного диффузионного тока гидрохинона от его концентрации.

Постояннотоковый вариант. V ячейки 3 мл

концентрации.

Переменнотоковый вариант. V ячейки 3 мл

Табл. 2. Результаты проверки метода прямой переменнотоковой кулонометрии на примере гидрохинона способом "введено-найдено". Объем ячейки 3 мл

С гидрохинона введенная, моль/см3	H пика, отн. ед.	i0, А	Q ∞ , Кл	C гидрохинона найденная, моль/см3
1∙10–7	48	1.49∙10–4	0.0248	8.6∙10–8
3∙10–7	162	5.20∙10–4	0.0837	2.89∙10–7
5∙10–7	270	8.37∙10–4	0.1395	4.81∙10–7

Из представленной таблицы с результатами видно, что найденные значения концентраций гидрохинона в растворе хорошо соответствуют введенным.