Метод прогнозирования изменений параметров временных рядов в цифровых информационно-управляющих системах

Задача прогнозирования заключается в нахождении будущих значений параметров временного ряда на интервале, называемом горизонтом прогнозирования [1, 2], в пределах которого обеспечивается необходимая точность решения задачи. Для непрерывных процессов это интервал ( t, t + t ], который для временного ряда записывается как ( n, n + А ]. Здесь t и nT - текущие моменты времени, при этом T - период дискретизации. Прогнозирование обычно осуществляется по значениям временного ряда или процесса на конечном, предшествующем, интервале [ t - T, t ] времени.

Горизонт предсказания является не только одной из важнейших мер качества прогноза, но и используется в качестве критерия степени детерминированности и случайности наблюдаемых явлений, служит характеристикой динамического хаоса (характеристикой хаотических колебаний в динамических системах). В основе этого утверждения лежит зависимость горизонта предсказания не только от используемых алгоритмов, но и от свойств анализируемых временных рядов и процессов. В задачах прогнозирования выбор алгоритма осуществляется исходя из соображений максимизации горизонта прогнозирования и достоверности прогноза. Один из принципов прогнозирования временных рядов или процессов основывается на их представлении непрерывными или дискретными моделями. В работах [1,

• 2 ] модель прогнозируемого процесса схематически описывается дифференциальным уравнением, зависящим от неизвестных параметров системы a и факторов f k , отражающих неопределённость модели, где k – номер анализируемого фактора, находится в пределах 1 <  k <  M и идентифицируется методом наименьших квадратов. При этом в рассмотрение вводятся три процесса: наблюдаемый процесс y , исследуемый процесс x и модельный (прогностический) процесс z . Исследуемый процесс в силу неопределенности факторов f k является (из множества возможных) неизвестным решением дифференциального уравнения

P (d/d t , x , a , f_k ) = 0.

Пренебрежение указанными факторами позволяет получить дифференциальное уравнение, описывающее модельный процесс z , при соответствующих условиях близкий к исследуемому процессу x . Это уравнение можно записать в виде

G (d/d t , z , a ) = 0.

Здесь критерием качества прогнозирования может являться среднеквадратическое значение нормы отклонения модельного процесса по факторам f k от исследуемого на интервале предсказания, то есть величина [1]

• 2\       1 M t +^T                       2

• ( x - z ll / ,,^ J l x ⁽ v , f k ) - z ⁽ v )l ^d v .              ⁽¹⁾

M k = i t

Аналогично определяется качество прогнозирования дискретных процессов или временных рядов, представленных дискретными моделями, которые, в частности, могут быть получены из непрерывных моделей путём замены производных конечными разностями. При этом операция интегрирования заменяется операцией суммирования по конечному множеству данных на интервале прогнозирования. Переход к дискретной модели эквивалентен численному решению дифференциального уравнения со свойственными этому решению проблемами чувствительности к возмущающим воздействиям.

На практике построение моделей основывается на данных о соответствующих наблюдаемых процессах: модели могут относиться к классам линейных дискретных и регрессионных систем, стационарных и нестационарных процессов. При решении задач прогнозирования нестационарных процессов может быть применен метод, основанный на декомпозиции процессов по эмпирическим модам (метод EMD) [5].

Распространенными методами прогнозирования являются параметрические методы регрессионной аппроксимации [4], динамические модели авторегрессии – скользящего среднего [3], методы импульсных функций [6] и искусственных нейронных сетей [9, 10].

1.    Нейросетевые методы прогнозирования

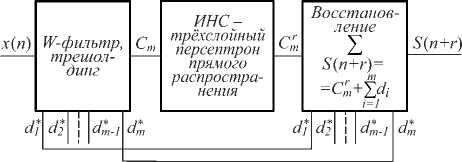
Горизонт прогнозирования любой модели зависит от того, насколько достоверно эта модель воспроизводит динамику временного ряда или системы, порождающей наблюдаемый процесс. Поэтому в этой части работы исследуется вопрос о горизонте прогнозирования на основе модели искусственной нейронной сети [7, 8]. Проблема здесь заключается в том, насколько точно динамика процесса может быть представлена весовыми коэффициентами сети. Поэтому обратные связи формируются алгоритмами обучения методом обратного распространения ошибки. Алгоритм функционирования многослойной нейронной сети прямого распространения при прохождении сигналов по направлению от входа к выходу задаются уравнениями в матричной форме. Соответственно, схема нейронной сети представлена на рис. 1.

В соответствии с рис. 1 вектор выходов j- го слоя сети, состоящего из p j нейронов,

У/=(Ул,У12",yj,pjT , (2) и вектор весовых коэффициентов l-го нейрона j-го слоя сети wjl =( wj, 1, wj 2, -, wj, pj) T . (3)

Тогда синаптическая сумма l-го нейрона j-го слоя сети sj,l = wjj yj-1 + wj,l,0 , (4) где wj,l,0 – смещение нейрона.

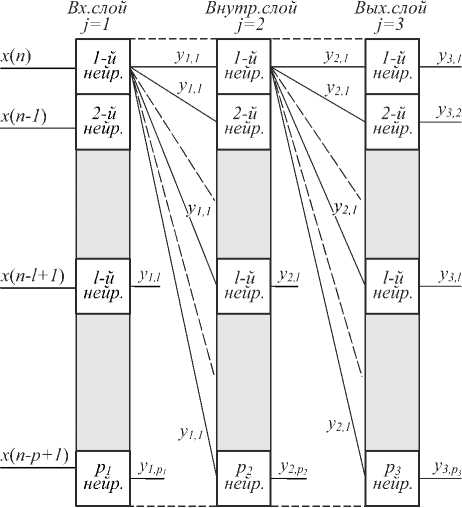
Рис. 1. Структура трехслойной нейронной сети обратного распространения ошибки

При этом выходы j-го слоя сети можно представить вектором yj =

' Q ^{( w} T лУн

Q ^{( w} T2 y j - i

_vQ ^{( w} T , p j y j - i

+ j o )

+ ^wj 2 o )

⁺ wj.P, 0) ,

где ф ( - ) - функция активации.

Формула (5) является рекуррентным уравнением, позволяющим найти последовательно выходы всех слоёв сети, начиная с первого слоя (j' = 1) и заканчивая последним слоем (в рассматриваемом случае j =3), совпадающим с выходом сети. Вектор y 0 – это входная последовательность временного ряда x ( n ).

При решении задач прогноза выходами сети в пределах одного цикла её функционирования являются результаты предсказания временного ряда или процесса на заданное число шагов вперёд, начиная с 1 и кончая p вых.сл . (число нейронов в выходном слое сети).

Алгоритм обучения нейронной сети методом обратного распространения ошибки также можно представить уравнениями в матричной форме.

Введём матрицу весов j -го слоя сети

Wj=( wjl, wj^V", wj. Pj) , вектор смещения нейронов j-го слоя wjo =(wjio, wj.2.0,", wj,pj,o )T , вектор синаптических сумм sj=(sj,1, sj2,", sj, P,) T и векторную функцию активации j-го слоя

Ф(s j ) = (ф(sj,1), Ф(sj,2 ),", Ф(sj,Pj ))T .

Задача обучения сети заключается в нахождении весовых коэффициентов j- го слоя сети путем минимизации функционала

p j            P j 2

—=Е e- = Е( yj - y-) = l=1             l=1

= ( v ( s j ) - y j ) T ( ф ( ^s j ) - y j ) ,

ной ряд x ( n ) отсчетов значений процесса. Аналогично могут быть исследованы непрерывные функции либо временные ряды данных, отображающие информацию изменения параметров различных процессов для решения задач прогнозирования в информационно-управляющих системах.

Табл. 1. Алгоритм обучения многослойного персептрона

где e - = v ( to jl y j - + to j _{0 l} ) - y _l или соответственно e jl = ф (s j _l ) - y j - вектор ошибок по выходам j- го слоя, У j = ( У 1 , У - ,2 , ^ , У ,,p j ) T — вектор требуемых выходов j -

го слоя сети.

Если ввести матрицы W j =d s T / d y j _{- 1}, диагональную матрицу Ф j = 5ф T ( s j )/ d s j в виде

5ф ^т ( s j ) d s -

=diag

дф ( S j ,1 )

&- ,1

дф ( s j ,2 )

&- ,2

. 5ф ( s - j

’ ^{d s}- , Pj .

,(11)

то алгоритм обучения методом обратного распространения ошибки принимает вид разностного уравнения

e - — 1 = W j ^ф - e - ,

с начальными условиями e j = ф ( s j ) - y j , при j =j вых.сл. (номер выходного слоя сети).

Коррекция весовых коэффициентов сети по ошибкам, полученным с помощью уравнения (12), осуществляется градиентным методом по итерационным формулам wj.i(q+1) = wj, 1(q)- а hj, 1(sj, 1) ej, 1 у j-1,

Этап обучения	Шаги алгоритма
1. Определение выходов (прямой проход)	У - =	Г ф ( w T 1 У - - 1 + W 01 ) ^ ф ( w T 2 у - - 1 + w 02 ) vф ( w Tp y j - 1 + w jp ) j	, - = 1,2,...; y 0 = C „
2. Определение ошибок (обратный проход)	e j - 1 = W j ® j e J , e - = Ф ( S j ) - У - , s j = W ^ У ) ! + w ) 0 = ( s - 0 , S - 2 ,..., s jp j ) T , где wj = ( w - 1 , w - 2 ,., w -p- ) - матрица весовых синаптических коэффициентов.
3. Коррекция синаптических коэффициентов	w j ( q + 1) = wH ( q ) - a h l ( s jl ) e -— , — q + 1) = w - 0 ( q ) -а Ф , e - , ,. .дф ( s -1 ) дф < s -- 2 ) 5(P ( S p X. дф T ( s j ) Ф , = diag (---- j--j—... -----—) =----- j—, d s,,     d s,2       d s,„          d s, J ,1             j , 2                j , p j                     j j дф ( s jl ) h jl ( s jl ) = „ , d s jl a - шаг настройки, выбирается в диапазоне 0< a < 1 .

w - ,0 ( q + 1) = w - ,0 ( q ) — а Ф - e j ,

h„l(sj,i) =^, dSji где l =1,2,...,pj,e-,i является l-м компонентом вектора ej ошибки, q - номер итерации, a - шаг настройки весовых коэффициентов, a выбирается в диапазоне 0

Таким образом, выражения (2) -(13) формируют алгоритм обучения нейронной сети при прогнозировании изменения значений исследуемой функции, реализуемый нейронной сетью, построенной по правилу многослойного персептрона.

Шаги алгоритма сведены в табл. 1.

Рис. 2. Структурная схема нейросетевого прогнозирования изменений значений функции

Входные сигналы в виде непрерывной функции x(t) или дискретной функции в виде временного ряда x(n) подаются на W-фильтр предварительной обработки вейвлет-преобразованием [6]. В W-фильтре формируются аппроксимирующие коэффициенты Ci,, вычисленные по формуле

2. Структура прогнозирования на трехслойном персептроне

Структурная схема, реализующая нейросетевое прогнозирование изменений значений параметров функции с её предварительной вейвлет-обработкой, представлена на рис. 2.

Как видно из рис. 2, система прогнозирования, реализованная на трехслойном персептроне прямого распространения, используется применительно к задаче мониторинга информации в информационно-управляющих системах, которая формирует времен-

Ci= 1 Ci_1фi(2it - n), p где фi(2it - n) - скейлинг-функция - коэффициент ортонормирования, обеспечивающий единичную норму скейлинг-функции. Детализирующие коэффициенты i-го уровня вейвлет-разложения вычисляются по формулам:

d₁= — x (n )у₁(2t - n),

p

1 -■ di = —^Ci-1Vi(2it -n).

P i=2

где уi(2it - n) - вейвлет-функция, m – максимальный уровень вейвлет-разложения.

Аппроксимирующие коэффициенты Ci подаются на вход N-разрядного регистра сдвига, построенного на элементах задержки с передаточной функцией Z^–1, в котором формируется выборка входных сигналов нейронной сети в виде движущегося окна из N отсчетов, обработанных в W-фильтре. На выходах выходного слоя нейронной сети вычисляются сигналы в виде аппроксимирующих коэффициентов прогноза C_m^*r , где r – число периодов прогноза (r = 1, 2,…, 10, при P3 = 10).

Многослойный персептрон состоит из входного слоя, внутреннего слоя (где значение j внутреннего слоя принимает значение 0 или 1) и выходного слоя. При j = 1 структурная схема персептрона представляет собой трехслойный персептрон. Увеличение числа слоев, т.е. j > 1, в персептроне приводит к увеличению вычислительных затрат при незначительном уменьшении погрешности [7].

Число нейронов во входном слое персептрона влияет на число анализируемых входных аппроксимирующих коэффициентов временного ряда Cm(n), соответственно на время анализа предыдущих значений отсчетов исследуемой функции, на общую погрешность прогнозирования. В соответствии с [7] погрешность прогноза при r =10 достигает |5|< 5%, в случае числа нейронов во входном слое pвх = 64, внутреннем слое pвнутр = 10, выходном слое pвых = 10. При уменьшении числа нейронов во входном слое до pвх = 32 погрешность повышается до |§| < (7...10)% .

Полученные аппроксимирующие коэффициенты прогноза C_m^*r с учетом необходимых для разных выходов нейронной сети задержек сравниваются с входными значениями Cm, что обеспечивает формирование ошибок предсказаний e^*r на всех p выходах нейронов выходного слоя нейронной сети.

При этом формализуем процедуру вычисления нейронной сетью аппроксимирующих коэффициентов прогноза, вычисление ошибок на выходах нейронов каждого из слоев, а также процедуру адаптивной настройки синаптических весовых коэффициентов, для каждого 1-го нейрона в рамках всех слоев нейронной сети.

Аппроксимирующий коэффициент прогноза на один период вычисляется на выходе l-го нейрона выходного слоя в соответствии с выражением:

*1 m

= У 31 =Фз(51о) =

1 + exp(-5-ю)

На выходе 1-го нейрона выходного (3-го) слоя вычисляется ошибка предсказания на один период – e₃^*₁¹, по которой вычисляется ошибка на выходе 1-го нейрона предыдущего 2-го слоя нейронной сети –e21.

Ошибки на выходе 1-х нейронов 2-го и 1-го слоев вычисляются в соответствии с выражениями:

64                    10

e-i = £ w21 ■ e21 e21 = ^ W31 ■ e31.

1=1                           1=1

Вычисленные таким образом ошибки обратного прохода, в свою очередь, адаптивно перестраивают синаптические коэффициенты связей между нейронами различных слоев. Таким образом, веса 1-х нейронов каждого слоя адаптивно настраиваются в соответствии с выражениями:

w 31 = W31 +a e31

d Ф3( 51o) ds10

*1 C_m

d Ф2( 510 )

w 21 = w21 +a e21 — ----y 21 , ds10

d Ф1( 564)

w 11 = w11 +a e_n — ----У11 .

ds64

Минимизация ошибки обеспечивается выше рассмотренной итерационной процедурой обучения нейронной сети, в ходе которой осуществляется настройка весовых или синаптических коэффициентов сети. Таким образом, задача прогнозирования заключается в оценивании будущих значений процесса по имеющимся данным Cm в текущий момент, в настройке значений коэффициентов нейронной сети по критерию минимальной величины ошибки предсказания, в оценивании управляемого объекта, основанных на сравнении выходных сигналов управляемого объекта C_m^*r и его модели, в качестве которой используется нейронная сеть.

Детализирующие коэффициенты di, вычисленные до уровня m (d1, d2, …, dm), после обработки алгоритмом сглаживания поступают на блоки восстановления выходного временного ряда прогноза.

Алгоритм сглаживания детализирующих коэффициентов по критерию адаптивного штрафного порога имеет вид:

di^*

d„ di > во;

0, di< Po,

где P0 = bлТ52 , a² - дисперсия шумовых составляющих во входном сигнале x(n), b – коэффициент пропорциональности, b = -J 2ln N, N - число периодов анализа.

Выходные сигналы с выходов нейронной сети в виде выходных аппроксимирующих коэффициентов C_m^*r (где r – номер выхода нейронной сети в соответствии с числом периодов прогноза rе[1,10]) также поступают на r-й блок восстановления выходного временного ряда прогноза. На выходе r-х блоков восстановления формируются выходные сигналы прогноза в виде временного ряда s(n+r) [7]:

⁵ (n + r) = p £

n

m

x (n )Vi(21 - n) +

+ZZ C-rf^t - n) + Z Cm * r ,

n i= 2

n

где r – число периодов времени прогноза, время прогноза определяется выражением tпрогн = rT.

Также в структурной схеме на рис. 2 представлен блок вейвлет-обработки временного ряда x(n) и блок восстановления выходного сигнала s(n) с пониженной погрешностью в соответствии с выражением восстановления:

^{5 (n}) = -^p

z

n

x (n )v1 (21 — n) +

m

+ ZZ Ci-1 -^(2-^ - n) + Z Cm n i=2                                n

В полученных выражениях (15) и (16), благодаря предварительной вейвлет-обработке в W-фильтре, существенно ослабляются флуктуации входного сиг-

нала x(n) за счет формирования аппроксимирующих коэффициентов m-го уровня Cm и подавляются компоненты шума, имеющие место во входном сигнале, путем обработки детализирующих коэффициентов алгоритмом сглаживания, что заметно снижает погрешность представления информации.

Таким образом, полученный очищенный от помех обработанный выходной временной ряд в реальном времени и обработанный выходной временной ряд прогноза представляют информацию в устройствах отображения и в системах принятия решений с более высокой точностью. Разработанный алгоритм нейросетевого прогнозирования изменения параметров временного ряда может быть реализован в различных программных средах, таких как MatLab Neural Network Toolbox, PyBrain и NeurophStudio.

Ошибки прогноза зависят от того, насколько размеры входного слоя ИНС соответствуют характерной величине интервала временного ряда, по которому можно восстановить его динамику, что подтверждается графиками на рис. 3 и рис. 4 [2].

_ 0-20 g 0,15 §_s OJO Is 0,05 to st

0      20      40     60      80 n

| ^-0J5 | -0,20 6 -0,25

-0,30

а)

б)

а)

0,5

0,4

0,3

0,2

0,1

-0,1

-0,2

0      20      40      60      80 n

Значения дискретного времени в виде нТ

Рис. 3. Результаты отклонения прогноза от исследуемого процесса при размере сенсорного слоя 64 нейрона (T – период дискретизации)

с^ 0,04 S +

0,03

!s

SS 0,02

Is 0,01

to §

0      20      40     60      80 n

Значения дискретного времени в виде пТ

о ^-0,02

б)

Рис. 4. Результаты отклонения прогноза от исследуемого процесса при размере сенсорного слоя 200 нейронов

Из рис. 3 и рис. 4 видно, что увеличение числа нейронов в первом (сенсорном) слое способствует увеличению горизонта и уменьшению отклонения прогноза от исследуемого процесса. Если для сети с 64 сенсорными нейронами (110 нейронов внутренний слой и 10 нейронов выходной слой) горизонт предсказания может быть принят равным в пределах 10T – 20T (рис. 3), то в случае 200 сен- сорных нейронов (110 нейронов внутренний слой и 10 нейронов выходной слой) (рис. 4) горизонт увеличивается до 100T.

Выводы

Существующие методы прогнозирования временных рядов и непрерывных процессов характеризуются большим разнообразием, что, в свою очередь, обусловлено большим разнообразием задач. Особый интерес в плане прогнозирования связан с представлением временных рядов моделями авторегрессии и нейронными сетями. В работе показано, что в рамках модели авторегрессии прогноз на несколько шагов вперед зависит от коэффициентов модели нелинейным образом. При этом задачу прогноза, состоящую в нахождении коэффициентов модели посредством минимизации целевой функции, можно решить итерационным методом. Поэтому интерес представляют сети, реализующие функцию рекуррентного минимизирующего отклонения оценок от наблюдаемых значений временного ряда. В данной работе рассмотрены искусственные нейронные сети, в частности, рассмотрены нейронные сети на персептроне с обратным распространением ошибки. В работе получены уравнения функционирования и обучения искусственной нейронной сети в матричной форме, получен алгоритм обратной подстановки, с помощью которого можно увеличить глубину прогноза. Результат моделирования и применения разработанного алгоритма заключается в повышении параметров результата прогнозирования изменений значений исследуемых функций по показателям длительности и погрешности получения прогноза, а также быстродействия, адаптивности системы при изменяющихся условиях. Дополнительным эффектом является также возможность гибкого изменения архитектуры нейронной сети в случае изменения требований на длительность прогноза.

Предложенная структурная схема реализации нейросетевого прогнозирования изменений параметров временных рядов с предварительной вейвлет-обработкой обеспечивает возможность достаточно точного мониторинга исследуемых процессов в информационно-управляющих системах.