Метод прогнозирования температурного состояния цилиндра при термообработке в условиях неполной исходной информации
Автор: Япарова Наталья Михайловна
Рубрика: Приборостроение, метрология и информационно-измерительные приборы и системы
Статья в выпуске: 2 т.19, 2019 года.
Бесплатный доступ
Предложен метод определения температуры при нелинейном теплопереносе внутри цилиндрического тела с неизвестной начальной температурой. Исходными данными являются результаты измерений температурных функций вблизи поверхности тела. Рассматриваемая задача возникает при термической обработке изделий в камерных печах. Математическая модель процесса включает в себя нелинейное уравнение теплопроводности, учитывающее зависимость теплофизических свойств материала от температуры, и граничные условия, характеризующие процесс теплообмена на поверхности тела. Для определения температуры внутри тела предложен метод дискретной регуляризации, позволяющий последовательно находить температуру в направлении от поверхности к оси цилиндра. Вычислительная схема метода предполагает использование стабилизирующих функционалов, а также конечно-разностных уравнений для определения температурных значений по пространственной переменной, что позволяет уменьшить влияние неизвестных начальных условий. Использование стабилизирующих функционалов позволяет обеспечить устойчивость вычислительной процедуры относительно погрешности исходных данных. В статье приведены результаты исследований устойчивости вычислительной схемы. С целью проверки принципиальной возможности определения температуры и получения экспериментальных оценок температурных погрешностей проведен вычислительный эксперимент. В эксперименте выполнен расчет температурного поля цилиндра с неизвестной начальной температурой, проведен сравнительный анализ найденных температурных функций с тестовыми значениями и получены экспериментальные оценки уклонений вычисленных температур от тестовых значений. Результаты вычислительного эксперимента представлены в работе, согласуются с теоретическими оценками и подтверждают эффективность и надежность предлагаемой вычислительной схемы.
Теплоперенос, обратная задача, метод регуляризации, метод обработки информации, устойчивость, оценка погрешности
Короткий адрес: https://sciup.org/147232254
IDR: 147232254 | УДК: 519.6 | DOI: 10.14529/ctcr190205
Текст научной статьи Метод прогнозирования температурного состояния цилиндра при термообработке в условиях неполной исходной информации
В современных технологиях, связанных с процессами теплопереноса, особое внимание уделяется процедуре температурного контроля объекта и выбору соответствующих температурных режимов, позволяющих реализовывать требуемые свойства объекта. Изучение влияния выбранных режимов на характеристики объекта, когда по результатам температурных измерений вблизи поверхности тела необходимо определить температуру во внутренних точках, вызывает большой интерес [1–5]. Математические модели теплопереноса, как правило, включают в себя уравнение или систему уравнений теплопроводности, граничные условия, формируемые из результатов измерений температурных функций вблизи поверхности и начальных условий, определяемых температурным состоянием тела в начальный момент времени. Задача определения температуры внутри тела по известному тепловому режиму, заданному на внешней поверхности, относится к классу обратных задач, и для ее решения необходимо использовать регуляризующие алгоритмы, позволяющие получать приближенные решения, устойчивые относительно погрешности исходных данных. С разработкой и исследованием методов решения обратных задач связаны работы многих исследователей [6–14]. Существенная особенность численных методов решения обратных задач заключается в том, что они разрабатываются с учетом известных начальных условий. С другой стороны, многие процессы теплопереноса связаны с ситуацией, когда в начальный момент времени невозможно измерить температуру внутри тела. Такая ситуация возникает при комплексной термообработке изделий на этапе отпуска или нормализации. Это приводит к возникновению задач с неизвестными начальными условиями.
В данной работе рассматривается задача определения температуры во внутренних точках цилиндрического тела, подвергаемого отпуску в процессе комплексной термообработки. Исходными данными являются результаты измерений, полученные от внешних температурных датчиков. В задаче требуется определить изменения температуры внутри тела при выбранном внешнем тепловом режиме воздействия на поверхность тела. Математическая модель теплопе-реноса включает уравнения теплопроводности, коэффициенты которого зависят от температуры, и граничных условий. Существенной особенностью данной задачи является наличие погрешностей в результатах измерения, а также отсутствие информации о начальной температуре тела.
В статье предложен метод определения температуры во внутренних точках по результатам поверхностных измерений. Метод основан на использовании конечно-разностных уравнений и регуляризирующих функционалов. Основная идея метода заключается в том, что, в отличие от существующих подходов, на каждом шаге неизвестная температурная функция определяется относительно пространственной переменной. Таким образом, схема позволяет одновременно найти температуру внутри рассматриваемой области вплоть до оси цилиндра и уменьшить влияние неизвестных начальных условий на результаты вычислений. Подобный подход был предложен в [15] в ситуации линейного теплопереноса при неизвестной начальной температуре объекта.
В работе показана локальная устойчивость метода при соответствующем соотношении шагов дискретизации и параметра регуляризации, приведены результаты сравнительного анализа получаемых температур с тестовыми значениями, а также получены оценки температурных погрешностей. Полученные оценки согласуются с теоретическими результатами и свидетельствуют о том, что предложенная вычислительная схема позволяет прогнозировать температуру во внутренних точках тела, подвергаемого внешнему тепловому воздействию.
Постановка задачи
В работе рассматривается задача, связанная с процессом теплопереноса в цилиндре радиусом I (рис. 1а). При термической обработке в печи тело подвергается внешнему тепловому воздействию, продолжительность воздействия ограничена величиной T . Температура в каждой внутренней точке A в текущий момент времени t характеризуется функцией u ( A , t ) .
Основные теплофизические свойства материала: теплоемкость, плотность и коэффициент теплопроводности в каждой внутренней точке A зависят от значения температуры в текущий момент времени t . Специфика процесса термообработки позволяет принять следующие допущения. Тепловое воздействие, осуществляемое через боковую поверхность дS ^ , одинаково в каждой точке дS i и достаточно велико по сравнению с тепловыми изменениями, получаемыми через торцы. Тепловое воздействие регулируется в каждый момент времени t и плотность тепловых потоков характеризуется функцией q ( t ) . Полагаем, что температура принимает постоянные значения вдоль любой прямой, параллельной оси цилиндра.
Принятые допущения позволяют свести задачу об определении температуры внутри тела к задаче распространения тепла в сечении цилиндра плоскостью, перпендикулярной оси цилиндра (рис. 1б).
Приборостроение, метрология…
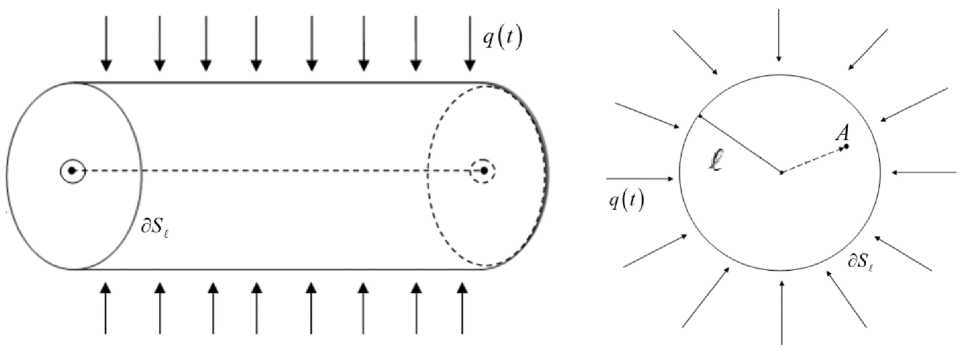
а)
б)
Рис. 1. Схема нагрева цилиндра
С у щ е ственн а я ос обе н н ость технологического процесса термообработки в печи заключается в сле д у ю ще м. Т е рмо об работк а в печи является промежуточным этапом ком п ле к с н ой т е рмоо б р аботк и , и к н а ча лу э того эта п а сохраняется влияние остаточных тепловых п роц е сс ов в о в н у т ре нн и х точк ах. У читы вая , что д ос ту п н ой д ля и зме ре н и я об ла с тью яв ляется только внешняя поверхн ость те ла , полу ча е м, что те м пература во внутренних точках в начальный мом ен т врем ени не мож е т быть п олу че н а и з ре зул ьта тов и з ме рен ий и яв ляе тс я н е и зв е с тн ой .
М а те ма ти чес ка я мод е ль р ассматриваемого процесса теплопереноса в п оля рн ой системе коо рд и н а т и м ее т след у ю щ ий в и д :
c ( u ) p ( u ) l u = 1 У x ( u ) r ^ u о t r о r V d r
, ( r , t ) e q t ; (1)
u ( t , t ) = p ( t ) , -X ( u ) d u d r , t ) = q ( t ) , t e [ 0, T ] , ( 2)
где r - тек ущи й ради ус , обла с ть Q t = (0, t ) x (0, T ), температурная функция u ( r , t ) - осесимметрична, коэффициенты c ( u ), p ( u ), X ( u ) соответствуют значениям теплоемкости, плотности и коэ ф фиц и е н та тепл оп ров одн ос ти в каждой точке тела в каждый момент вр е ме н и , фу н к ц и я p ( t ) формируется и з рез у льтатов и змерений температуры вблизи поверхности т е ла , а фу н к ц и я q ( t ) х а ра к т е ри зу е т п лотн ос ть те п ло вого потока на поверхности тела. В этой зад а че треб у е тс я н а й ти u ( r , t ) , удовл е тв оря ющ у ю ( 1 ) , (2) , а также те мпературу на оси цилиндра
u ( 0, t ) = ф ( t ), t e [ 0, T ] . (3)
2+Y i +Y J Y
Су щ е с т в ов ан и е т очного реш е н и я u 0( r , t ) e H ’ 2 ( QT ) Q H ’2 ( QT ) , ye (0,1), QT = [ 0, ^ ] x [ 0, T ]
задачи (1)–(3) при де й с тви те льн ых зн а че н и ях p 0( t ) и q 0( t ) доказано в работах [6], [16], а единст в енн ос ть реш е н и я в н е которой п од о б л а с ти D Е с QT обоснована в [6].
При н и ма я в о в н и ма н и е , чт о при термообработке изделия в камерных п е ч ах в с и лу и н е ртности т еп лоп е р е н ос а на гре в и зд елия происходит постепенно, а также учитыва я п род ол жи те льнос т ь и н а и боль ш у ю те мп е ра ту ру н агрева, полагаем, что имеют место следующие д оп у щ е н и я:
max| u ( r , t )| <Ф e e ( r + t ) , m ax ^ max| utt |,m ax| urr |,max |u rrr | ^< C . (4)
Q t I Q t Q t Qi J
При определении температуры u(r,t) во внутренних точках необходимо учитывать, что при проведении измерений вблизи поверхности тела неизбежно возникают уклонения измеренных величин pg , q5 от действительных значений p0 (t) и q0 (t). В математической модели эту ситуацию представим следующим образом. Вместо точных значений p0 (t) , q0 (t) известны некоторые приближения p5(t), q5(t) и 5 такие, что max{Hp0(t)-p5 H,Hq0(t)-q5 H}^S. Таким образом, необходимо по приближенным данным p5 (t), q5 (t) и 5 найти функцию u5 (r, t), удовлетворяющую (1), (2), а также температуру ф5 (t) на оси цилиндра.
Метод прогнозирования температуры
Вычислительная процедура прогнозирования температуры основана на методе дискретной регуляризации и заключается в следующем. Введем в рассмотрение конечно-разностную сетку:
G = ^
( ri,tj ) : r = ( N + 1 - 1 ) h , t = ( j - 1) т ;
_ h = £ / N; T = T / M; i = 1, N + 1; j = 1, M + 1, где h и т - шаги сетки по переменным r и т соответственно, а также множество дискретных функций V = {v(ri, tj ) = vi j}, заданных на G. Используя конечно-разностный аналоги частных производных, представим (1), (2) в следующем виде:
c i , j Р i , j
v i , j +1 - v i , j = X i +1, j -X i , j ( v +1, j v, j )
+ 1 , j V +1, j V , j
( i - 1 ) h h
T v i +1, j - v i , j h 2
+ X i , j
Vi+1, j 2 vi, j + vi-1, j h2
, i = 2, N , k = 1, M + 1.
qj
V 1, j = p j , V 2, j = p j - T—h , j = 1, M + 1. (6)
X 1, j
Учитывая характеристики технологического процесса и результаты, представленные в [17, 18], полагаем, что c ( u ), p ( u ), X ( u ) положительны, дважды непрерывно дифференцируемы в соответствующей области и определяются формулами:
c ( u i , j ) = с 0 + k c u i , j , р ( u i , j ) = Р о + k р u i , j , X ( u i , j ) = X 0 + k x u , , j
где значения с 0 = с ( u ( £ ,0 ) ) , р 0 =р ( u ( £ , t ) ) , X o =X ( u ( £ ,0 ) ) , а величины kc , k р , k X согласованы с соответствующими характеристиками, представленными, например, в [18].
Основная идея предлагаемого метода заключается в том, что на каждом следующем шаге итерационного процесса, используя (5), вычисляют значения vi + 1 j в точках ( ri + 1 , t j ) для всех j = 1, M :
v i +1, j
ci , j р , j ( i - 1) h 2 у- j +1 - у- j X i , j ( i - 1)
i j +--:------7---1--:------7------------ V ,- j - V i -1 j
, X i+1,j(i - 1)+ X i, j т X i+1,j(i - 1)+ X i, j ’ ’ начиная от точки (г,,tj), i = 3,N, расположенной вблизи внешней границы, к точке (rN+1,tj), расположенной на оси цилиндра. Коэффициенты c, j, р, j, X, j вычисляются по формуле (7).
Особенность задачи заключается в том, что непосредственное использование уравнения (8) не позволяет получать приближенные решения, устойчивые относительно погрешности исходных данных. Для обеспечения устойчивости метода поступают следующим образом. При вычислении коэффициента X , + 1 j в (8) используется модифицированное соотношение (7) с введенным в него стабилизирующим функционалом X , + 1j =X 0 + ( k X-a ) v , j , включающим параметр регуляризации a . Значение параметра а и величину h согласуют с т и 5 .
Устойчивость вычислительной схемы метода
Исследуем устойчивость вычислительной схемы, используя подход, принятый в теории регуляризации [2], [13], введя в рассмотрение функции wi , определяемые формулой wi+1=j mM+il Vi+1, j- Vi, j |.
Приборостроение, метрология…
Согласуем значение N , характеризующее дискретизацию по пространственной переменной, с количеством измерений ( M + 1 ) , а параметр регуляризации а выберем так, чтобы при известном значении ( M + 1 ) величина температурной погрешности удовлетворяла бы неравенству wN + i < K 5 , где K - некоторая константа. Введем следующие параметры:
S = max_ ^L ц = max---- X i'j J ( i 1 ) , n = max , c i’J P i ’ J ( i 1 ) h\ .
j = 1, M + 1 1 ’ j X i + 1, J ( i - 1 ) + X i , J i ’ j ( X i +1, j ( i - 1 ) + X i , j ) т
Выбираем а таким, что при всех i = 1, N + 1 и j = 1, M + 1 было выполнено условие
X i ,J
а < min , х . i,j ( i — 1 ) 1 V iJ
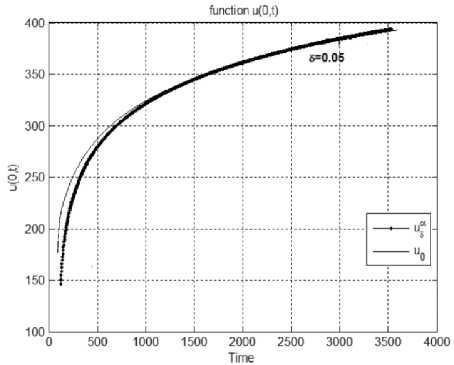
Учитывая теплофизические свойства процесса термообработки в печах, получаем, что ц < 1, тогда, имеет место следующая оценка wi+1 j=1,m Учитывая ограниченность функции u(r,t), из (4) получаем, что max | vi -+1 - vi - |< 2фet+T. (12) j=1,m Из (9)–(12), получаем w2 = max | v2 - v , |< max | q^h |< h(S + 5) < S + 5, j=1, m+1 ,J ,J j=1, m+1 J wi+1 < 2Фe^+T -^ + (S + 5)цi-1, i = 3, N +1. 1 -ц Тогда имеет место следующая оценка Wn+1 < 2рФ e <+T -1- + (S + 5)ц N-2, 1 -ц характеризующая величину погрешности численного метода решения задачи (1)–(3). Учитывая (9), (10) и то, что Xi+1 - = Х0 +(kx - a) vi -, выберем шаги дискретизации так, чтобы имело место условие п <---,. „. . Тогда получаем, что при выполнении следующего условия 2Фe^+T) h2 < 5 т “ 2Фe(^+T) __min i,j2J ^ i=2, N+1, j=1, M+1^ Ci, j pi, j J J имеет место оценка wN+1<--+ (S + 5)ц 1 -ц Принимая во внимание, что ц < 1, получаем, что при соблюдении условия N > 2 + 1одц K к — 5 ^1 -цJS + 5J где K > 1 +----, будет выполнено требуемое неравенство wN+1< K5 . Соотношения (13), (14) свиде- 1 - ц тельствуют о локальной устойчивости предлагаемого метода определения температур. Заметим, что аналогичные результаты были получены в работе [19] для задачи измерения определения температуры на поверхности цилиндра по результатам измерений на оси, связанной с диагностикой состояния температурного датчика. Это свидетельствует о том, что в отличие от методов, ориентированных на вычисления по переменной, характеризующей время, при изменении направления вычислений по пространственной переменной не требуется разработка принципиально новой вычислительной схемы, а достаточно ограничиться модификацией основной схемы. Оценка температурных погрешностей Оценим величину наибольшего возможного уклонения вычисленных температурных значений от действительных, используя величины si , определяемые формулой 5, = maxv, - и , i = 1, N +1, i j=1,M+1 i ’ j i ’ j где vi, j является приближенным решением задачи (5), (6), а ui, j соответствует действительным значениям температуры при текущем значении радиуса r = r в момент времени t = tj. Имеем , < ci, jpi, j (1 1) h22ф (^+t) 2 X1, j(i 1) — 5v + 2Ф e + 2 (X i+1, j(1 - 1)+X i, j )t X i+1,j(1 - 1)+X i, j c ,p,.,(i -1)h2 (Xz+1,.-Xz,-)(i -1)h + i,j^ jv ;----O+ 2 v i+1,j i,д----O(h) + Xi+1, j(i -1)+ Xi, j Xi+1, j(i -1)+ Xi, j (X/+1,-X,.,)(i -1)h2 , x2 Xzh +---~—2--—к-----(O (h) )2 +-----^Ц----O (h) (ui+1, j-ui, j)(Xi+1, j(i -1)+ Xi, j) Xi+1, j(i -1)+ Xi, j , Xi ,j( i - 1)h 2 O(h2). Xi+1, j(i - 1) + Xi, j Оценивая слагаемые в (15) и учитывая (13) и (14), получаем c,j pi,j (i - 1)h2 2фe(<+T) — 5. (xi+1, j(i - 1) + Xi, j )t Из (11), (15), определения ц и подхода к вычислению Xi+1j получаем: IXi+1, j-Xi, j I(i -1)—aI vi, j I(i -1)< Xi, j < ц— P ; Xi+1, j(i - 1) + Xi, j Xi+1, j(i - 1) + Xi, jXi,j1 -a I vi, j I(i -1) i -1 2 Xi, j(i -1) — ц Xi, j — Ц —Ц Xi+1,j(i - 1) + Xi,j Xi+1,j(i - 1) + Xi,j i -1 2 - X i+1,j -X i, j, Обозначим X = min___Xij. Учитывая, что--------- = kX, имеем i=1,N+1,j=1,M+1 ,J Ut+1,j - Ui,j X i+1, j -X i, j (i - 1) ui+1, j - ui, j Xi+1, j (i - 1) + Xi, j Отсюда и из соотношений (4), (15)–(18) следует, что 5i+1 —(1+2ц) 5i+8 + ПCt2 + 3цCh2+| k^C2+ЦC |h4 I, i = 2,N. V 2 Vх Учитывая (14), получаем при i = 2, N +1 \ s e 2 3Cpl2 kX C2l4 5,-11 — (1 + 2ц) 5,- + 6 + n Ct +--7—I i+1 ( ) i 2N2 „ XT, 2 3Cpl2kx C2l4Cц14 Полагаем T = n Ct + —H— + ——— +. 2N2 X* N4 Cpl4 2N4. . Тогда соотношение (19) имеет вид (i-2 5i+1 — (1 + 2ц)5i + 6 +T — (1 + 2ц)i-152 + ^(1 + 2ц)k (6 + T). Учитывая, что s7 = maxv, j=1, M+11 , j - V k =0 7 и2j | — 6 + h(6 + C), получаем, что для величины sN+1, харак- Приборостроение, метрология… теризующей наибольшее отклонение численного решения от истинных температур на оси цилиндра, имеет место следующая оценка: %+1 <(1 + 2ц) N-1 5 + I (5 + C) 2 + log + -12 .■'- \ Ч 5 + 5 4ц Из соотношений (14), (20) следует, что сходимость метода зависит от величины шагов дискретизации, следовательно, метод является условно сходящимся и для получения приближенного решения необходимо выбирать достаточно небольшие значения N . Из соотношения (20) следует, что величина sN+, соответствующая наибольшей температурной погрешности, будет достаточно велика на всем [0, T]. Это согласуется с результатами, представленными в [6], в соответствии с которыми невозможно получить единственное решение во всей области QT , а следовательно, невозможно точно оценить температурные погрешности во всей области QT , но возможно получить более точную оценку температурных погрешностей (оценку погрешности метода) только в некоторой подобласти Ds. Для получения уточненных оценок погрешностей был проведен вычислительный эксперимент на основе имитационного моделирования. Результаты эксперимента представлены в данной работе. Результаты вычислительного эксперимента С целью проверки принципиальной возможности определения температуры внутри тела по результатам поверхностных измерений и получения оценки температурной погрешности был проведен вычислительный эксперимент на основе имитационного моделирования. Методика эксперимента заключалась в следующем. На начальном этапе эксперимента находили решение прямой задачи: и(0,t) = Фо(t), u(I,t) = pо (t), t e[0,T]; и(r,0) = go(r), r e[0,4 Полученное решение u0(r, t) прямой задачи (21)–(23), характеризующее температурное поле цилиндра, и функцию Фо (t), соответствующую температуре на оси цилиндра, использовали в дальнейшем в качестве тестовых функций. На втором этапе эксперимента осуществляли моделирование функции q0(t), характеризующей внешнее тепловое воздействие. Ситуацию возникновения погрешностей в результатах измерения представляли следующим образом. В каждой точке tj формировали приближенные значения p5(t), q5(t), используя следующие формулы: p5 (tj)=pо(tj)+erp (tj), q 5 (tj)=q о(tj)+erq (tj). Величины erp (tj) и erq (tj) соответствуют значениям случайных величин, равномерно распределенных на [-5,5]. Предлагаемый подход к моделированию p5(t), q5(t), эквивалентен появлению аддитивных случайных погрешностей в результатах измерений вблизи поверхности цилиндра, уровень которых не превосходит величины 5. Полученные значения p5(t), q5(t) определяли исходные данные в задаче (1)–(3). На следующем этапе эксперимента находили приближенное решение и5 (r, t) задачи (1)-(3) по исходным данным p5 (t), q5 (t), 5 и вычисляли значения температурной функции и5( 0, t ) = ф5 (t). Функция и5 (r, t) соответствует прогнозируемым температурным значениям, получаемым в области из p5 (t), q5 (t) с помощью предлагаемого метода дискретной регуляриза- ции, а функция φδ (t) соответствует температурным значениям на оси цилиндра. На следующем этапе эксперимента проводили сравнительный анализ полученных численных решений uδ(r, t) и φδ (t) с тестовыми функциями. В работе представлены результаты вычислительного эксперимента, проведенного на основе имитационного моделирования в соответствии с предложенной методикой. В качестве эталонной модели рассматривался процесс теплопереноса в цилиндре радиуса I = 1, помещенного в камерную печь, разогретую до температуры 400 °С. Теплофизические характеристики материала c(u), ρ(u), λ(u) соответствовали характеристикам стали марки Ст45, [17], [18]. Продолжительность процесса составила T = 60 мин. При решении прямой задачи (21)–(23) полагали, что начальной температуре тела соответствовало значение u (r,0) = 25 °С, r е [ 0, I]. При формировании тестовой функции p(t) , φ(t), а также функции q(t) использовали результаты, представленные в [20]. Результаты вычисления температурного поля цилиндра uδ(r, t) , полученные в подобласти Dес QT, De=[0, Z]x(e, T-е) при 5 = 0,05 с помощью предложенной вычислительной схемы, а также тестовая функция u0(r, t) представлены на рис. 2а. Поверхность Exact solution соответствует графику тестовой температурной функции u0(r, t) , а поверхность Regularized solution представляет график приближенного решения uδ(r, t) задачи (1)–(3), соответствующие прогнозируемым температурным значениям в подобласти Dε. Exact Solution Regularized Solution а) б) Рис. 2. Температурное поле цилиндра Результаты вычисления температур на оси цилиндра φδ (t) и график тестовой функции φ0(t) при t ∈ (ε,T - ε) представлены на рис. 2б. Обозначение u0 соответствует графику тестовой функции φ0(t) , а обозначение uδα – графику численного решения φδ (t) задачи (1)–(3). Как отмечалось ранее, невозможно точно оценить температурные погрешности при всех t∈[0,T] , получить оценку погрешности метода возможно только в некоторой подобласти (ε,T - ε) . В эксперименте был проведен сравнительный анализ тестовой температурной функции φ0 (t) , заданной на оси цилиндра, и температурной функции φδ (t) , вычисленной на оси. Для про- ведения сравнительного анализа φ0(t) и φδ (t) в эксперименте были использованы величины Δ и Θ , определяемые формулами: Δ= max φδ(t) - φ(t) , Θ= t∈(ε,T -ε) max t∈(ε,T -ε) φδ(t) - φ(t) |φ(t)| Приборостроение, метрология… Величина А соответствует наибольшей оценке отклонений температур, найденных с помощью предложенного метода во внутренних точках цилиндра, от тестовых значений. Результаты сравнительного анализа при различных значениях 5 и N и е = 0,03T представлены в таблице. Оценки температурных погрешностей 5 N А 0 0,05 5 27,95 0,2023 6 26,86 0,1944 7 25,56 0,1850 8 20,72 0,1511 9 2·1056 – 10 0,5·10123 – 0,1 5 29,54 0,2307 6 27,12 0, 2118 7 26,08 0,2037 8 21,76 0,1691 9 0,5·105 – 10 2·10133 – Используя величины А и 0, определяемые формулой (24), получили, что при 5 = 0,05 для рассматриваемого примера величина температурных погрешностей на оси цилиндра составила А « 21 °С, и 0 = 0,15 при е = 0,03T, а при е = 0,06T значения этих величин составили А « 9 °С, и 0 = 0,05 соответственно. Таким образом, результаты вычислительного эксперимента свидетельствуют о том, что предложенный метод позволяет с достаточной точностью находить требуемую температурную функцию u (r, t) во внутренних точках цилиндрического тела при соблюдении условий согласования величин шага дискретизации h, параметра регуляризации а с интервалом измерения т, а наибольшие значения оценок температурных погрешностей являются достаточно точными в интервале (е, T -е). Заключение В работе рассмотрена математическая модель теплопереноса внутри цилиндрического тела с неизвестной начальной температурой и предложен метод определения температурного состояния тела по исходным данным, известным на поверхности. Вычислительная схема метода основана на использовании конечно-разностных уравнений и включает регуляризующий алгоритм идентификации коэффициентов. Показана локальная устойчивость метода, а также найдена теоретическая оценка погрешности метода, соответствующая оценке наибольшего отклонения вычисленных температур от действительных значений. В работе представлены результаты вычислительного эксперимента, которые согласуются с теоретическими результатами и свидетельствуют о том, что предложенная вычислительная схема позволяет прогнозировать температуру во внутренних точках тела, подвергаемого внешнему тепловому воздействию с достаточной точностью. Работа выполнялась при финансовой поддержке Министерства образования и науки Российской Федерации прикладных научных исследований в рамках базовой части Государственного задания «Разработка, исследование и реализация алгоритмов обработки данных динамических измерений пространственно-распределенных объектов», техническое задание 8.9692.2017/8.9 от 17.02.2017.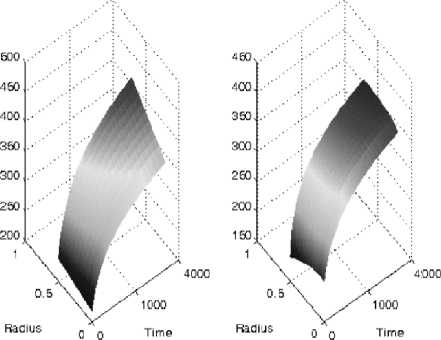
Список литературы Метод прогнозирования температурного состояния цилиндра при термообработке в условиях неполной исходной информации
- Алифанов, О.М. Обратные задачи теплообмена / О.М. Алифанов. - М.: Машиностроение, 1988. - 280 с.
- Самарский, А.А. Вычислительная теплопередача / А.А. Самарский, П.Н. Вабищевич. - М.: Едиториал УРСС, 2009. - 784 с.
- Шестаков, А.Л. Методы теории автоматического управления в динамических измерениях / А.Л. Шестаков. - Челябинск: Издат. центр ЮУрГУ, 2013. - 257 с.
- Мартинсон, Л.К. Температурное поле цилиндрического тела в режиме периодического разогрева / Л.К. Мартинсон, О.Ю. Чигирёва // Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия «Естественные науки». - 2015. - № 3 (60). - С. 88-98.
- Лукин С.В. Режим нагрева и термостатирования слябов в печи при горячем посаде / С.В. Лукин // Металлург. - 2018. - № 7. - С. 54-58.
- Лаврентьев, М.М. Некорректные задачи математической физики и анализа / М.М. Лаврентьев, В.Г. Романов, С.П. Шишатский. - М.: Наука, 1980. - 286 с.
- New approaches to error estimation to Ill-posed problems with application to inverse problems of heat conductivity / K.Y. Dorofeev, N.N. Nikolaeva, V.N. Titarenko, A.G. Yagola // Journal of Inverse and Ill-posed problems. - 2002. - Vol. 10, no. 2. - P. 155-169.
- DOI: 10.1515/jiip.2002.10.2.155
- Кабанихин, С.И. Прямые и итерационные методы решения обратных и некорректных задач / С.И. Кабанихин, М.А. Шишленин // Сибирские электронные математические известия. - 2008. - Т. 5. - С. 595-608.
- Солодуша, С.В. Численное решение обратной граничной задачи теплопроводности с помощью уравнений Вольтерра I рода / С.В. Солодуша, Н.М. Япарова // Сибирский журнал вычислительной математики. - 2015. - Т. 18, № 3. - С. 327-335.
- Марчук, Г.И. Методы вычислительной математики / Г.И. Марчук. - СПб.: Лань. - 2009. - 608 с.
- Вабищевич, П.Н. Монотонные разностные схемы для задач конвекции / диффузии / П.Н. Вабищевич // Дифференциальные уравнения. - 1994 - Т. 30, № 3. - С. 503-515.
- Тихонов, А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. - Изд-во МГУ, 1999. - 799 с.
- Численные методы решения некорректных задач / А.Н. Тихонов, А.В. Гончарский, В.В. Степанов, А.Г. Ягола. - Изд-во МГУ, 1990. - 115 с.
- Табаринцева, Е.В. Об оценке точности метода вспомогательных граничных условий при решении граничной обратной задачи для нелинейного уравнения / Е.В. Табаринцева // Сибирский журнал вычислительной математики. - 2018. - Т. 21, № 3. - С. 293-313.
- DOI: 10.1134/s1995423918030059
- Yaparova, N. Method for temperature measuring in the rod with heat source under uncertain initial temperature / N. Yaparova // 2016 International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2016. - Proceedings 7911716.
- DOI: 10.1109/ICIEAM.2016.7911716
- Ладыженская, О.А. Линейные и квазилинейные уравнения параболического типа / О.А. Ладыженская, В.А. Солонников, Н.Н. Уральцева. - M.: Наука, 1967. - 736 с.
- Марочник стали и сплавов / А.С. Зубченко, М.М. Колосков, Ю.В. Каширский и др.; под общ. ред. А.С. Зубченко. - М.: Машиностроение, 2003. - 784 с.
- Лившиц, Б.Г. Физические свойства металлов и сплавов / Б.Г. Лившиц, В.С. Крапошин, Я.Л. Линецкий. - М.: Металлургия, 1980. - 320 с.
- Япарова, Н.М. Численный метод решения обратной задачи с неизвестными начальными условиями для нелинейного уравнения теплопроводности / Н.М. Япарова // Вестник Южно-Уральского государственного университета. Серия «Вычислительная математика и информатика». - 2016. - Т. 5, № 2. - С. 43-58.
- DOI: 10.14529/cmse160204
- Исаченко, В.П. Теплопередача / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. - М.: Энергия, 1975. - 488 с.


