Метод расчета акустических напряжений при шестилучевой дифракции в слоистых средах

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2018PNRPU MECHANICS BULLETIN

Определение упругих постоянных тонких пленок [1, 2], исследование критических напряжений в пленках [3, 4], разработка новых электроакустических и акусто-оптических преобразователей [5, 6] и некоторые другие проблемы тесно связаны с расчетом напряженно-дефор-мированного состояния пленки, вызванного упругими волнами. Распределение напряжений в твердом слое зависит от вида возможных упругих волн. Как известно [7, 8, 9], в любом направлении изотропной среды могут распространяться упругие волны трех типов, различающихся направлением колебаний частиц среды. В продольной волне (обозначаемой как волна P -типа) колебания происходят вдоль направления волнового вектора. В волнах сдвига амплитудный вектор колеблется перпендикулярно волновому вектору. Если в сдвиговой волне колебания направлены перпендикулярно или параллельно плоскости падения, то волна называется соответственно горизонтально поляризованной (SH-тип) и вертикально поляризованной (SV-тип) волной сдвига.

При падении продольной или сдвиговой волны на слой твердого тела, часть энергии отражается и проходит через слой в виде волн того же типа, что и падающая волна. В дополнение к этим волнам изотропный слой может преобразовать P-волну в вертикальную волну сдвига и наоборот [8, 10]. Анизотропия упругих свойств среды распространения приводит к возможности взаимного преобразования волн всех трех типов. Соответствующие исследования для сред, обладающих орторомбической и тригональной симметриями проводились, например, в работах [11, 12]. В любом направлении анизотропной среды скорости распространения трех волн могут различаться друг от друга, и их поляризации не являются ни чисто продольными, ни чисто поперечными. Волна, у которой направления колебаний наиболее близки к направлению волнового вектора, называется квазипродольной. Две другие волны называются квазипоперечными [5]. В анизотропном слое конечной толщины d в результате воздействия плоской упругой волны образуются шесть волн (по три в направлении отражения и пропускания), суммарное воздействие которых формирует напряженное состояние слоя.

В расчетах распространения волн в слоистых средах получил развитие подход, основанный на матричном методе решения системы дифференциальных уравнений [13, 14]. Описание этого метода применительно к упругим волнам имеется в обзорах [11, 15] и монографиях [16-18]. Согласно этому методу значения компонент вектора смещения и тензора напряжений на одной границе слоя выражаются через аналогичные компоненты на противоположной границе с помощью так называемой матрицы переноса T = exp(Wd), где W- матрица n-го порядка, составленная из коэффициентов соответствующей системы дифференциальных уравнений. Относительно просто решается задача рассеяния горизонтальной волны сдвига изотропным слоем [18], которая описывается матрицей переноса второго порядка. Для матрицы переноса четвертого порядка, определяющей рассеяние P-SV-волн изотропным слоем, также известна аналитическая формула [19]. Эти матрицы переноса, как и их аналоги из оптики (см. например [20, 21]), находятся вычислением матричной экспоненты exp (Wd) по формуле Лагранжа-Сильвестра [13] с помощью собственных значений Ху., j = 1,...,n, матрицы W в виде функции T = T(exp(X1 d),...,ехр(Хиd)). В случае матрицы W общего вида, порядок которой n > 4, решение алгебраической задачи на собственные значения возможно только численными методами. Поэтому результат вычислений матрицы переноса по формуле Лагранжа–Сильвестра отягощен погрешностями вычислений собственных значений и экспонент exp(Xjd). Похожие проблемы возникают, если для вычислений матричной экспоненты воспользоваться методом Бэкера–Вандермонда [22], интерполяционной формулой Ньютона [23], методом Лапласа [24], канонической формулой  Жордана [13]. Указанные погрешности накапливаются при вычислении матрицы переноса всей структуры T = TNTN_X TTX с ростом числа слоев N и величин параметров распространения кji = X jdi, где dt, i = 1,...,N, - это толщины слоев. В рассматриваемой задаче Xj имеют смысл волновых чисел, и, следовательно, размерность модуля параметра распространения пропорциональна произведению частоты излучения и толщины. Возрастание именно этих величин может приводить к неудовлетворительным результатам при вычислении матрицы переноса и зависящих от нее величин (см. статью [25] и библиографические указания в ней). Это одна из причин, по которым перечисленные выше именные методы, известные из учебной и справочной литературы, практически не применяются для вычислений матричных экспонент большого порядка.

Проблема вычисления матричной экспоненты является центральной при решении больших систем дифференциальных уравнений в различных приложениях. Это стимулирует развитие известных методов расчетов, сравнительный анализ которых имеется в работах [26, 27], и разработку новых подходов, примеры которых рассмотрены в статьях [28–35]. Из набора известных методов наилучшим численным подходом к нахождению матричной экспоненты exp( Wd), по мнению авторов обзора [28], является алгоритм масштабирования и кратного квадрирования (МКК): 1) масштабирование матрицы Wd ^ Wd / (m2) с целью понижения ее нормы, 2) вычисление экспоненты масштабированной матрицы ехр(Wd / (m2)), 3) вычисление T = [exp(Wd / (m2))]m с помощью кратного квадрирования. В методе МКК при выполнении второго этапа подразумевается использование аппроксимации Паде или аппроксимации разложения в ряд Тейлора конечной суммой. Примеры реализаций этих способов расчетов представлены в работах [36, 37]. Метод расчета [36] реализован в математическом пакете MATLAB и используется некоторыми исследователями [35] для сравнительного тестирования своих алгоритмов.

В данной работе для вычисления матрицы переноса упругих волн применяется метод многочленов главных миноров [38], который, по крайней мере для матриц порядка n <  9 [39], обеспечивает более надежное и точное вычисление матричной экспоненты в сравнении с методами [36, 37].

1.    Метод вычислений 1.1.    Основные уравнения

Динамика напряженно-деформированного состояния упругой среды описывается уравнениями движения и законом Гука. Эти уравнения в декартовой системе координат выражаются формулами а2 ui = л 8^

a t ²    g = 1 d X g ’

• 1    [ a Hl     aU- । i ।

T I    +    l = LL s higi ^G a ’

• ²    l ^d x i   ^d x )    g = 1 , = 1

• h , i , j = 1,2,3,

  
  

где p - плотность; t - время; x , x ₂, x₃ - декартовы координаты; u i , с _gi и s_higj ( g , h , i , j = 1,2,3) - компоненты вектора смещений, тензора напряжений и тензора упругой податливости соответственно.

Уравнения (1) решаются применительно к плоскослоистой среде, у которой плотность и упругие параметры среды зависят только от одной координаты x вдоль оси, перпендикулярной поверхности анизотропного слоя (рис. 1):

p = p ^{( X}3 ), s higj = s higj ^{( X} 3 )-                   ⁽²⁾

Деформации в анизотропном слое 0 <  x ₃<  d порождаются плоской волной:

u o = A o exp^[ i ^(k 0 • r ^{- to t} )].                ⁽³⁾

падающей из области   x ₃<  0 . Здесь u₀, A_o, k₀ =

= k₀ jCj + k ₀₂e₂ + k ₀₃e₃ и о являются соответственно вектором смещений, амплитудным вектором, волновым вектором и циклической частотой падающей волны; i – мнимая единица.

Решение задачи (1)–(3) методом разделения переменных показывает, что все величины н и сgh имеют одинаковую зависимость от переменных x , x и t в виде exp[i(k^x + k^x^ — tot)], как в падающей волне. Поэтому если обозначить через Vi(x3) (i = 1,...,9) неизвестные зависимости компонент вектора смещений и тензора напряжений от координаты x , то указанные компоненты принимают вид u2 , ^23 , U,U3 ,013 ,^33 ,^11 ,^22 ^ =

= v j ( Х 3 ) exp[ i ( k 01 x , + k ₀₂ x ₂ - to t )],           (4)

где индекс j принимает значения от 1 до 9 в том же порядке, в каком перечислены компоненты вектора смещений и тензора напряжений в левой части равенства (4).

С учетом равенств (4) уравнения (1) редуцируются в систему уравнений d T (x3) dx

= W T ( x ₃),

T ( X 3 ) =

V 1 ( ^x 3 )

V 2 ⁽ x 3 )

V 3 ^{( x} 3 )

V 4 ⁽ x 3 )

V 5 ^{( x} 3 )

V 6 ^{( x} 3 )

	w 11	w 12	w 13	w 14	w 15	w 16
	w 21	w 11	w 23	0	w 25	w 26
W =	w 25 w 26	w 15 w 16	w 33 w 43	w 34 0	w 35 w 36	w 36 w 46	,
	w 23 0	w 13 w 14	w 53 0	0 w 64	w 33 w 34	w 43 0	(5)

Vi ( x ₃) = a 1 Vi ( x ₃) + a _{z 2} V2 ( x ₃) + a ₃ V3 ( x ₃) + + a_z. ₅v₅ ( x ₃) + a ₆V6 ( x ₃), i = 7,8,9,

^{где w}n    i ^{( k} 01 a 92 ^{+ k} 02 a 82 ), w 12 ^S 14 a 72 ^{+ S} 24 a 82 ^{+ S} 46 a 92 ⁺

+ S44, w13 =—i (k01 a72 + k02 a92), W14 = — ik02, w15 = S14 a75 + + S24 a85 + S46 a95 + S45 ,    w16 = S14 a76 + S24 a86 + S46 a96 + S34 , w21 = k01Y6 + k02Y4 - 2k01k02Y5 — pto ,    W23 = k01Y3 — k02Y5 +

^{+ k} 01 ^k 02 ^{( Y} 6 ^—Y 1 ), w 25 = ^— i ^{( k} 01 a 95 ^{+ k} 02 a 85 ), ^W 26 =^— i ^{( k} 01 a 96 ⁺

^{+ k} 02 a 86 ), ^W 33 = ^— i ^{( k} 01 a 75 ^{+ k} 02 a 95 ),    w 34 = ^{— ik} 01 , w 35 =

= ^S 15 ^a75 ^{+ S} 25 ^a85 ^{+ S} 56 a 95 ^{+ S} 55 , w 36 = ^S 15 a 76 ^{+ S} 25 a 86 ^{+ S} 56 a 96 ⁺

^{+ S} 35 ,     ^W 43 = ^{— i ( k} 01 ^a 76 ^{+ k} 02 ^a 96 ),     ^W 46 = ^S 13 a 76 ^{+ S} 23 a 86 ⁺

^{+ S} 36 ^a 96 ^{+ S} 33 , w 53 = ^k 01 ^Y 1 ^{+ k} 02 ^Y 6 ^{+ 2 k} 01 ^k 02 ^Y 3 ^{— pto} , ^W 64 = ^—pto и использованы обозначения: S_gh – компоненты тензора упругой податливости в матричной форме [40]; ^a 71 = i ^{( k} 01 ^Y 3 ^{— k} 02 ^Y 2 ),     ^a 72 = ^S 24 ^Y 2 ^{— S} 14 ^Y 1 ^{— S} 46 ^Y 3 ,     a 73 =

= i ⁽ k 01 ^Y 1 + k 02 ^Y 3 ), ^a 75 = S 25 ^Y 2 ^{— S} 15 ^Y 1 ^{— S} 56 ^Y 3 , a 76 = ^S 23 ^Y 2 ^{— — S} 13 ^Y 1 ^{— S} 36 ^Y 3 , ^a 81 = i ^{( k} 02 ^Y 4 ^{— k} 01 ^Y 5 ),   ^a 82 = ^S 25 ^Y 2 ^{— S} 24 ^Y 4 ⁺

^{+ S} 46 ^Y 5 , ^a 83 =^{— ik} 01 ^Y 2 ^{— ik} 02 ^Y 5 , a 85 = ^S 15 ^Y 2 ^{— S} 25 ^Y 4 ^{+ S} 56 ^Y 5 , ^a 86 = ^S 13 ^Y 2 ^{— S} 23 ^Y 4 ^{+ S} 36 ^Y 5 , ^a 91 = ^ik 01 ^Y 6 ^{— ik} 02 ^Y 5 , a 92 = ^S 24 ^Y 5 —

^S 14 ^Y 3 ^S 46 ^Y 6 , ^a 93 = ^ik 01 ^Y 3 ^{+ ik} 02 ^Y 6 , ^a 95 ^S 25 ^Y 5 ^S 15 ^Y 3 ^S 56 ^Y 6 , ^a 96 = ^S 23 ^Y 5 ^{— S} 13 ^Y 3 ^{— S} 36 ^Y 6 ; ^Y j = ^ j ^{/( S} 11 ^ 1 ^{— S} 12 ^ 2 ^{+ S} 16 ^ 3 ), j = 1,...,⁶; A 1 = S 22 S 66 ^— S 26 , A 2 = S 12 S 66 ^— S 16 ^S 26 , A 3 = S 12 S 26 — ^S 16 ^S 22 , ^A 4 = ^S 11 ^S 66 — ^S 16 , ^A 5 = ^S 11 ^S 26 ^{— S} 16 ^S 12 , A 6 = S 11 S 22 — S 122 .

• 1.2.    Матрица переноса

Решение системы уравнений (5) в матричной форме имеет вид

T(d2) = TT(d),       d2 > d,(7)

где

T = I + J W (x) dx3 + J W (x) J W (^) d ^ dx, + d1                        d1

d2           x3

+ J W (x3) J W (51) J W (52) d ^2 d 51 dx3 + d1             d1

в теории дифференциальных уравнений называется матрицантом, а в теории волн в слоистых средах – матрицей переноса. Здесь и далее I обозначает единичную матрицу шестого порядка.

Если структура толщиной d состоит из N однородных слоев, т.е. W = W = const,, d^i< x3 < d, то T( d) = T T(0), где T = TnTn—r-71, T = exp[W(d — dz_i)], i = 1,--,N и матричная экспо- нента определяется формулой

22   33

exp( Wd ) = I + Wd + -d- + Wd - + .

= Z W4" ■ (9) j = 0 ^j !

Соотношения (7)–(9) позволяют выразить значения функций Vi( x ₃),•••,V₆( x ₃) через значения этих функций на глубине x₃ = 0 . После этого нахождение значений функций v? ( x ₃), Vs ( x ₃), V9 ( x ₃) по формулам (6) не представляет труда.

• 1.3.    Вычисление матрицы переноса однородного слоя

T ( x ₃) = exp( Wx₃ ) в данной работе проводится по формуле

T ( x 3 ) =

m

5 (WY  \ ( 1     ^{6 +} N 1 1 h                     1

2 | Wx ³Illi + 27^ p 6 — h + g B j — 1 — g (6)I ■ (10) h = 0 V m /  \ ^h •    j = 6 j • g = 0                    у

Здесь Pj, j = 1, • - - ,6, являются коэффициентами характеристического уравнения матрицы Wx / m . Как известно, коэффициенты характеристического уравнения матрицы равны с точностью до знака суммам соответствующих главных миноров этой матрицы, в частности px равен следу матрицы, а p6 =- det(Wx3 / m). Вслед- ствие этого функции B (6), определяемые рекуррент- ными уравнениями [38]

B 1 (6) = B 2 (6) = . - B ₄(6),   В 5Ю = 1,

^B j (6) = f P g B j - g (6), j >  6, g = 1

называются многочленами главных миноров.

Для выполнения расчетов по формулам (10)–(11) требуется предварительное нахождение матриц ( Wx ₃ / m )², ( Wx / m )³,  ( Wx / m )⁴, ( Wx / m )⁵ и коэффициентов p .

Эти коэффициенты вычисляются рекуррентно по методу Леверье [13]. Для каждой из найденных матриц (Wx3 / m)j определяется след s j и применяются формулы jPj = sj- P1 sj -1-----Pj-1 si, j = Г-Л (12)

Выражение (10) получено из точной формулы в результате усечения ряда ^J 6('“) до конечной суммы ^6+N1^"). Порождаемая таким усечением относитель ная погрешность е в вычислениях элементов матрицы переноса зависит от числа N1 и удовлетворяет неравенству [41]

m р N1 +1

(6 + N 1 ) R N = 1 (6 + h )’

где р = 8,5dго /(m min v), min v «1/ Jp max S - мини- мальная скорость распространения упругих волн в рассматриваемом слое. Параметр масштабирования m яв- ляется минимальным целым, которое выбирается в соответствии с условием р < 1. Пример оценки параметра масштабирования для кристаллического слоя кремния представлен в статье [41]. Выбор N1 = 14 обеспечивает вычисление матрицы переноса с помощью алгоритма (10)–(12) с двойной арифметической точностью 10–16, а N1 = 25 соответствует четверной арифметической точности 2,5×10–32. Для реализации этого метода требуется выполнение четырех матричных перемножений. Для сравнения Алгоритм 2.3 [36], использующий для вычисления матричной экспоненты аппроксимацию Паде, требует выполнения шести матричных перемножений плюс решение одного матричного уравнения. При этом нормализованная относительная погрешность превышает 10–16.

• 1.4.    Геометрия рассеяния

Из равенств (4) следует, что лучи всех волн, возникающих в слоистой среде, лежат в одной плоскости ( х ₃, ^ ) (рис. 1, а ), и проекции волновых векторов на оси x и x определяются соответственно формулами k_jX = k oi = k o sin 6₀ cos a , k^ = k ₀₂ = k ₀ sin 6₀ sin a . Если обозначить 6. угол между волновым вектором k_y и осью х ₃, то kj 3 = kj cos 0 j , где k. = | k j | и углы 6 j определяются законом преломления (отражения):

kj sin 6j = k ₀ sin 6₀. (14)

Рассмотрим случай, когда области x ₃<  0 и x ₃ >  d , ограничивающие анизотропную слоистую структуру, являются изотропными средами.

а                        б                      в                     г

Рис. 1. К определению направляющих косинусов падающей волны: a - углы падения 6₀ и a ; б – падающая волна SH-типа; в – падающая волна SV-типа; г – падающая волна P -типа

Fig. 1. To defining the direction cosines of an incident wave: a - angles of incidence 6₀ and a ;

b – SH-type of the incident wave; c – SV-type of the incident wave; d – P-type of the incident wave

Как известно, в любом направлении изотропной среды могут распространяться волны P-, SH- и SV-типа, скорости распространения которых  vp = го^(2ц + Х)/р, vSH = Vsy = го^ц/p, определяются упругими постоянными Ламе: X и ц. В результате воздействия падающей волны на анизотропный слой в изотропных областях х3 < 0 и x3 > d могут возникнуть от двух до шести волн (рис. 2):

U = Aj exp[i(k. • r -гоt)], kj = kj 1e1 + kj2e2 + kjзез, j = 1V6, где A j и k j – соответственно амплитудные и волновые векторы; индексами 1 и 4 обозначены горизонтальные волны сдвига, индексы 2 и 5 соответствуют вертикальным волнам сдвига, наконец, индексы 3 и 6 отмечают продольные волны. Волновые числа этих волн имеют следующие     значения:

| k з | м^р ₍2 п + X о ), | k 6 1 = ^p d /(2 ц d + X d ) . На

I ^k 1 1 = 1 k 2 1 = ®^Р о / Ц о ,

I k4 M k5 |= ^Pd / Цd , рисунках направления ко- лебаний амплитудных векторов A волн SH-, SV-и P-типа показаны стрелками зеленого, синего и красного цветов соответственно.

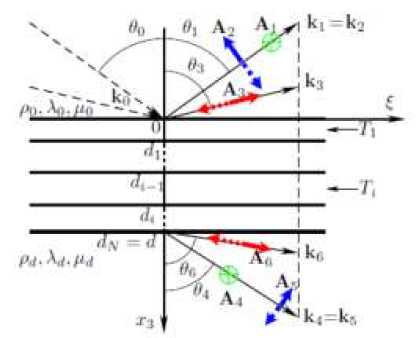
Рис. 2. К определению направляющих косинусов рассеянных волн: А 1 и А 4 – амплитудные векторы SH-волн, А 2 и А 5 – амплитудные векторы SV-волн, А 3 и А 6 – амплитудные векторы P -волн

Fig. 2. To defining the direction cosines of the scattered waves, А 1 and А 4 are the amplitude vectors of SH waves, А 2 and А 5 are the amplitude vectors of SV waves, А 3 and А 6 are the amplitude vectors of P waves

• 1.5.    Граничные условия

Упругие свойства изотропных сред (компоненты тензора упругой податливости) выражаются через постоянные Ламе. С помощью последних уравнения закона Гука (1) существенно упрощаются, и напряжения a_z3 в изотропных областях х₃ <  0 и х ₃ >  d выражаются через компоненты вектора смещения формулами

I 8и . 8u. )

Qn = ц L +   3  ,     i = 1,2, i 3     (dx3

diu    | dud c33 = (2ц + Х)—3- + Xl+ — dх3     ( dxx5

где X = X_o , ц = ц₀ , если x ₃< 0 и X = X_d , ц = ц^ , если х ₃ >  d .

Смещения частиц среды в этих изотропных средах обусловлены волнами, которые в них распространяются. Таким образом, в области х₃<  0

u = u о + u i + u 2 + u 3 , Ц о * 0;

u = u о + u 3, Цо = 0, в области х3 > d u = u4 + u5 + u6, цd * 0;

^u = ^u 6 ,   Ц d = ⁰

Подстановка векторов (16) и (17) в уравнения (15) позволяет найти компоненты тензора напряжений на границах анизотропного слоя. Следовательно, используя соотношения (3), (4), (15), (16) и (17), несложно выразить значения неизвестных функций У j ( х ₃) на границах х₃ = 0 и х₃ = d анизотропного слоя через амплитуды рассеянных волн. Так, для случая, когда ц₀ * 0, ц_а * 0, такой подход дает следующий результат:

• ^У 1 ⁽⁰⁾    c 02 A 0 ⁺ c 12 ^A 1 ⁺ c 22 ^A 2 ⁺ c 32 ^A 3 ,

У 2 (⁰) = Ц 0 A 0 E ^{( C} h 2 k h 3 ⁺ C h 3 k h 2 ) C ih h = 0

У 3 ⁽⁰⁾ = c 01 A 0 ⁺ c ii A i ⁺ c 21 A 2 ⁺ c 3i A 3 , у ₄ (0) = c ₀₃ A + c ₁₃ A ₁ + c ₂₃ A 2 + c ₃₃ A ₃,

У 5 (⁰) = Ц 0 A 0 EE ( C h 1 ^k h 3 ⁺ C h 3 k h 1 ) C ih , h = 0

^У 6 ⁽⁰⁾ = A 0 E 2 ^Ц 0 ^C h 3 k h 3 ^{+ X} 0 E c hg k hg h = 0 L                      g = 1

^C ih ^,

У 1 ( d ) = C 42 A 4 ⁺ С 52 A 5 ⁺ C 62 A 6 ,

У 2 ⁽ d ) = Ц d A 0 E ^{( C} h 2 ^k h 3 ^{+ C} h 3 ^k h 2 ) ^C ih , h = 4

У 3(d ) = C 41A4 + C51A5 + C 61A6, у 4 (d) = C43 A4 + C53 A5 + C63 A6 ,

^У 5 ^{( d} ) = ^Ц d A 0 E ^{( C} h 1 ^kh 3 ^{+ C} h 3 ^k h 1 ) ^C ih , h = 4

6                               3

У 6(d) = A0 E 2ЦdCh3kh3 +Xd E chgkhg h=4 _                      g=1

^Cih ^,

где c _gh – направляющие косинусы амплитудных векторов А д волн, A_h = | A _h |, h = 1,...,6, C_ih = A_h I A ₀. В последней формуле индексы i = 1,2,3 указывают три возможных типа падающей волны. Значение i = 1 соответствует SH-волне (см. рис. 1, б ), в которой направляющие косинусы амплитудного вектора с ₀₁ = sin а ,   с ₀₂ =- cos а ,   с₀₃ = 0;

i = 2 соответствует SV-волне (см. рис. 1, в) с направляющими косинусами  с01 = cos 00 cos а,  с02 = cos 00 sin а, с03 = - sin 00; и i = 3 соответствует P-волне (см. рис. 1, г) с направляющими    косинусами    с01 = sin 00 cos а, с02 = sin 00 sin а, с03 = cos 00. Рис. 2 определяет направляющие косинусы амплитудных векторов рассеянных волн:        си = sin а,        с12 =- cos а,        с13 = 0, с21 =- cos 0t cos а,    с22 =- cos 0t sin а,    с23 =- sin 0г, с31 = sin 03 cos а,      с32 = sin 03 sin а,      с33 =-cos 03, с41 = sin а,   с42 = - cos а,    с43 = 0,    с51 = cos 04 cos а, с52 = cos 04 sin а,      с53 = - sin 04,      с61 = sin 06 cos а, с62 = sin 06 sin а, с63 = cos 06.

• 1.6.    Вычисление коэффициентов преобразований волн

В результате подстановки выражений функций V,- (0),   V, ( d ), из формул (18) в уравнение Т ( d ) =

= T ( d ) Т (0) получается система алгебраических уравнений относительно амплитуд волн A . Решение этой системы, например, по методу Гаусса дает значения коэффициентов преобразований C падающей волны в рассеянные волны. Энергия волны пропорциональна квадрату модуля амплитуды. Поэтому величина C_ih ² характеризует долю энергии падающей волны, передаваемой h -й волне, и называется интенсивностью h -й волны.

• 1.7.    Вычисление акустических напряжений

• 2.    Результаты расчетов

  Представленный алгоритм расчетов был использован в исследовании акустических напряжений в кристаллических слоях. Некоторые результаты вычислений для слоев молибдата свинца и кремния показаны на рис. 3–6. Все значения амплитуд | a j 3 | колебаний компонент тензора напряжений даны в единицах A 10¹⁵ Па. Циклическая частота ® = 2п10 7 Гц. Плоскость х₃ = 0 совпадает с гранью кристалла (001). Параметры кристаллов, использованные в расчетах, представлены в таблице, и области х ₃<  0, х ₃<  d предполагались твердыми с параметрами 1 ₀ = 1 d = 1,67 - 10¹⁰ Н/м², ц_о = ц^ = 3,27 х х 10¹⁰Н/м², р₀ = p_d = 2,65 - 10³кг/м³.

Вычиление акустических напряжений на глубине х3 производится по формуле Т(х3) = T(х3 )У(0), где значения компонент матрицы У(0) определяются из (18) с учетом найденных коэффициентов преобразований C .

Параметры кристаллов Parameters of crystals

Кристалл	ρ	S 11	S 12	S 13	S 16	S 33	S 44	S 66
PbMoO 4	6950	21	–12,4	–4,93	–15,5	16,6	37,5	40,6
Si	2329	7,69	–2,14	–2,14	0	7,69	12,58	12,58

Примечание: плотность кристалла ρ, кг/м ³ ; компоненты тензора S gh , 10 ^–12 Па ^–1 .

На рис. 3–5 представлены результаты расчетов напряжений на границах слоя PbMoO 4 толщиной d = 0,000924 м, возникающих при падении на этот слой горизонтальной волны сдвига (см. рис. 3), вертикальной волны сдвига (см. рис. 4) и продольной волны (см. рис. 5). Зависимости |а,.₃(0)| = |а,.₃(0)|(9_О) отмечены на рисунках цифрами 1 , 2 , 3 , соответствующими значению индекса i у компонент тензора напряжений. На рис. 3–5, a показаны зависимости энергетических характеристик С 2 (9₀) волн, рассеянных в область х ₃<  0 , а на рис. 3–5, б – соответствующие характеристики волн, рассеянных в область х ₃ >  d . На этих рисунках кривые С 2 (9₀) отмечены цифрами 1, 2, 3, 4, 5, 6 , соответствующими значениям индекса j . Кроме этого, функциональные зависимости С ²1 ( 9 ₀) и С 4 ( 9 ₀) интенсивностей горизонтальных волн сдвига изображены зеленым цветом, интенсивности вертикальных волн сдвига С ²2( 9 ₀) и С ²₅( 9 ₀) нарисованы синим цветом, а для показа интенсивностей С ²2 (9₀) и С 2 (9₀) продольных волн использован красный цвет. Такие же цвета используются в рис. 6.

В результате перерассеянии волн на границах кристаллического слоя рассеянные волны могут усиливаться или, наоборот, ослабляться за счет интерференции. Число таких экстремумов возрастает с увеличением толщины и уменьшением скорости распространения волн. Наряду с системой интерференционных максимумов и минимумов на рис. 3 и 4 видны экстремумы резонансного характера. Причиной их возникновения является следующее.

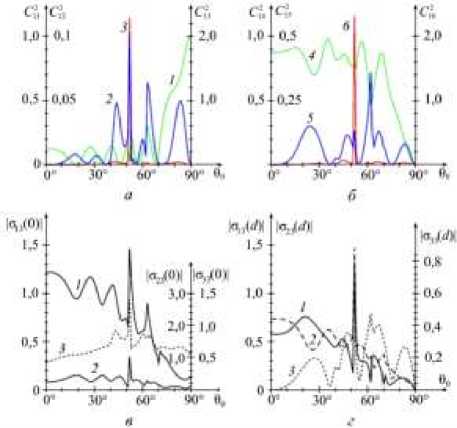
Рис. 3. Амплитуды напряжений, возникающих на границах слоя PbMoO 4 под воздействием горизонтальной волны сдвига: а = 38 ° , d = 0,000924 м

Fig. 3. Amplitudes of stresses arising at the boundaries of PbMoO 4 layer under the influence of a horizontal shear wave: а = 38 ° , d = 0,000924 m

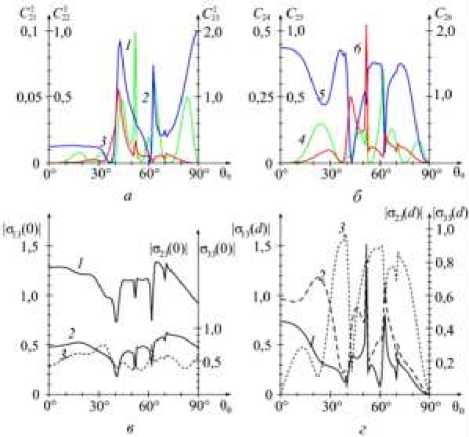
Рис. 4. Амплитуды напряжений, возникающих на границах слоя PbMoO 4 под воздействием вертикальной волны сдвига: а = 38 ° , d = 0,000924 м

Fig. 4. Amplitudes of stresses arising at the boundaries of PbMoO 4 layer under the action of a vertical shear wave: а = 38 ° , d = 0.000924 m

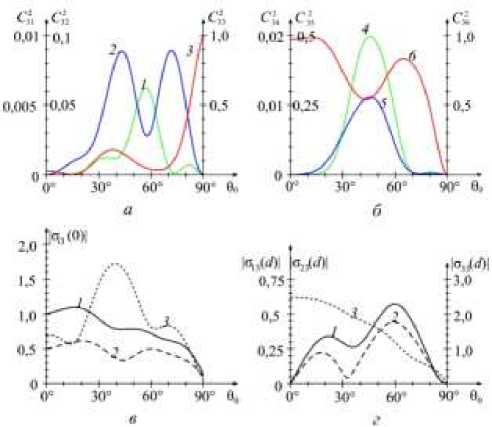
Рис. 5. Амплитуды напряжений, возникающих на границах слоя PbMoO 4 под воздействием продольной волны:

а = 38 ° , d = 0,000924 м

Fig. 5. Amplitudes of stresses arising at the boundaries of PbMoO4 under the action of a longitudinal wave:

а = 38 ° , d = 0.000924 m

Если сдвиговая волна падает на кристалл под углом 90 > 0ОС (критический угол 90С определяется в соответствии с законом (14) равенством sin 90С = k3 / k0), то продольные волны, генерируемые кристаллом, становятся неоднородными, распространяющимися вдоль оси £ . Для рассматриваемой структуры 90С = 39,15°. При определенной толщине кристаллического слоя и углах падения суммарное смещение вертикальных волн сдвига внутри кристалла создает поперек слоя мо- дулированную структуру. Дифракция продольных волн на этой структуре порождает резко выраженные экстремумы в спектрах рассеянных волн при некоторых углах падения 90 > 90с . Именно этим объясняются резко выраженные экстремумы напряжений в спектрах рассеянных волн. Корреляции между экстремумами кривых С2 = С2 (90), с одной стороны, и экстремумами функций |оа(9)| = |аа(°)|(90) и |ая(d)| = |аа(d)|(90) -с другой, определяются формулами (18) и хорошо видны при сравнении рис. 3, a и рис. 3, в, рис. 3, б и рис. 3, г, рис. 4, a и рис. 4, в, рис. 4, б и рис. 4, г.

На распределение энергии падающей волны между волнами, рассеянными кристаллом, большое влияние оказывает также вращение плоскости поляризации сдвиговой волны по мере прохождения кристаллической среды. Одним из проявлений этого эффекта являются равенства С 2 = С 2 и С 2 = С 2₄ , которые выполнялись с высокой точностью во всех численных экспериментах, проведенных в рамках данной работы и [41]. Иллюстрациями сказанного являются синяя кривая на рис. 3, a и зеленая кривая на рис. 4, a , синяя кривая на рис. 3, б и зеленая кривая на рис. 4, б . В результате вращения плоскости поляризации сдвиговой волны падающая волна SH -типа ( SV -типа) при отражении или пропускании полностью может превращаться в волну SV -типа ( SH -типа). Пример такого преобразования горизонтальной волны сдвига кристаллическим слоем кремния показан на рис. 6. При углах падения а = 44 ° и 9₀ = 42,7232 ° коэффициент С 2 = 0, т.е. отраженная от кристалла сдвиговая волна является вертикально поляризованной.

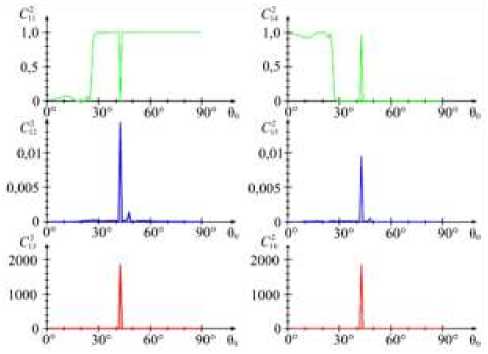
Рис. 6. Интенсивности волн, излучаемых слоем Si под воздействием горизонтальной волны сдвига а = 44 ° , d = 0,000845 м

Fig. 6. The intensities of waves emitted by a Si layer under the influence of a horizontal shear wave а = 44 ° , d = 0.000845 m

Амплитуды всех других волн резонансно увеличены. Продольные волны являются неоднородными, их волновые векторы направлены вдоль поверхностей кристалла x3 = 0 и x3 = d . Эти волны энергию от кристаллического слоя не переносят. При указанных условиях на границах кристаллического слоя кремния возникают резонансы напряжений. Амплитуды колебаний этих напряжений имеют следующие значения: 1^3(0)| = 16,3, | ^з(0)| = 15,8,         |сзз(О)| = 4,8,         |^1з( d )| = 16,4,

I^с2 з( d )| = 16,2, 1^₃(0)| = 5,4. Ширина резонансов спектров рассеяния, показанных на рис. 6, и соответствующих им резонансов напряжений равна примерно пяти угловым секундам.

Заключение

Такие эффекты, как полное преобразование поляризации сдвиговой волны, дифракционные резонансы, которые возможны при шестилучевой дифракции упругих волн в анизотропном слое, происходят в очень узком диапазоне АО_о углов падения О_о . Положение такого диапазона АО_о может быть изменено за счет не