Метод расчета дисперсионных кривых, волновых полей и упругих параметров среды в скважинах с радиально- неоднородной зоной нарушения

Существует целый ряд методов расчета, дисперсионных кривых для радиальнонеоднородных волноводов. Например, метод трансфер-матрицы позволяет решить эту задачу для радиально-слоистых волноводов [1]. В применении к задачам скважинной акустики он подробно описан и широко применялся в работах Сина [2]. В случае волноводов со свободными границами дисперсионные кривые удобно находить как решение задачи на собственные значения [3,4]. Для неограниченных волноводов, у которых радиальная зависимость упругих параметров представляется кусочно-непрерывными функциями, одним из наиболее удобных способов вычисления дисперсионных кривых является метод матричного уравнения Риккати [5]. В данной работе он применялся совместно с методом продолжения по параметру, что позволило вычислять и разделять дисперсионные кривые [6].

Неоднородность упругих свойств породы вблизи скважины оказывает значительное влияние на. дисперсионные кривые нормальных мод. В задачах акустического каротажа, область такой неоднородности получила название зоны нарушения. Для характеризации изменения упругих параметров среды в данной зоне часто рассматриваются модели скважин с радиально-неоднородными упругими свойствами. Обычно внутри такой зоны предполагается малое отклонение скоростей продольных и поперечных объемных волн от аналогичных в неповрежденной породе. Это предположение позволяет воспользоваться методами теории возмущений для восстановления профиля подобных скоростей. Идея такого подхода, заключается в формулировке и решении линеаризованной системы алгебраических уравнений, описывающих зависимость малых изменений собственных частот нормальных мод, вызванных наличием зоны нарушения, от основных параметров, характеризующих возмущения упругих свойств породы вследствие ее повреждения. В методе дипольного радиального профилирования указанный подход позволил вычислять с приемлемой точностью профили упругих параметров в зоне нарушения на. основании измеренной дисперсионной кривой изгибиой моды в скважине [7,8]. В отличие от метода, описанного в этих работах, где теория возмущений применялась к уравнениям теории упругости в их интегральном представлении, в данной работе такой метод применяется к матричному уравнению Риккати. В случае радиально-неоднородных сред использование данного метода упрощает постановку обратной задачи и ускоряет ее решение.

В цилиндрической системе координат (радиус-вектор т = (т,0,г) удобно представить зависимость фурье-представлений для векторов смещений n = (п_г, пу, п_г) и нормальных напряжений Д = (ст_тт , a_rg, a_rz) от коордииат 0. г и времени t в вине дДСЖ-: щу Символы к и v обозначают волновое число вдоль оси г и азимутальное волновое число соответственно, а ш — круговую частоту. Применяя такое представление решения управляющих уравнений, можно показать, что эволюция матрицы акустического импеданса среды Z (т), определяемой как Д (т) = Z (т) п, подчиняется матричному уравнению Риккати [5]:

+ ZЛZ + ZQ + SZ + P = 0. ат

Выражения для матричных коэффициентов Л, Q, S и P имеют следующий вид:

/А + 2д  0  0 А 1          1 / у  ivy  iAy А

Л =     0 д 0    , Q = — iv -10   ,

0    0  д               ^т A  0   0

1    2дуА 1  iviA

S =        ivy    2   0,

'  \   iAy     01

p = дш²і — 1

E —ivE — 2 іАуд

ivE v 2E + А2д Avд (1 + 2y)

2 іАуд

Avд (1 + 2y) A2E + v2 д

где символ I есть единичная матрица, и ввелены следующие обозначения: y = А (А + 2д)-1. E = 4д (А + д) (А + 2д)-1 и A = кт. Здесь А (т), д (т) ид (т) — радиальные профили параметров Ламэ и плотности среды соответственно. В качестве одного из возможных начальных условий для уравнения (1) удобно рассматривать матричный импеданс упругой полости Zp (т2) на внешней границе т = т2 зоны нарушения. Решением возникающей при этом задачи Коши на внутренней границе т = щ является матрица Z (тД. Рассматривая жидкость, заполняющую скважину, в качестве импедансной нагрузки на границе т = щ, характеризуемой матрицей Zp (тД, придем к дисперсионному уравнению:

det [Z (тД — Z _L (тД] = 0.

Матрицы Z p (т2) и Z l (тД имеют смысл матричных импедансов цилиндрической полости в упругой среде с радиусом т2 и жидкого цилиндра радиусом щ. Они могут быть точно вычислены для любых заданных значений к, v и ш. Корни уравнения (3) удобно вычислять и разделять методом продолжения по параметру [6], корректируя решение на каждом шаге с помощью метода Давиденко [9]. Для любых значений к, v и ш, удовлетворяющих уравнению (3), радиальный профиль матрицы Z (т) внутри неоднородного слоя вычисляется по формуле (1). Его подстановка в уравнение движения и закон Гука приводит к следующим эволюционным уравнениям для векторов Дип:

dn ат

= [Л (т)Z (т) + Q (т)] п,

(4а)

da ат

— [P (т) Z-1 (т) + S (т)] Д.

(4Ь)

Чтобы избежать рассмотрения решения уравнений (1) в точках неограниченного роста элементов матрицы импеданса ( Zij ^ то), удобно воспользоваться преобразованием Кэли K (т):

K (т) = (iaI — Z (т)) (iaI + Z (т))-1,

где размерность константы а совпадает с размерностью матрицы импеданса Z (г). Данная константа может выбираться произвольно, например, она может определяться как а = ш р (г_а) Ct (г_а), г де Ct (г Д и р (г_а) - локальная скорость поперечных волн и плотность среды в точке г = г_а. Норма матрицы K (г) ограничена для физически допустимых вещественных величин к, v и ш. После применения преобразования Кэли уравнение (1) принимает вид матричного уравнения Риккати для матрицы K (г). Входящие в него матричные коэффициенты линейно выражаются через матрицы Л, Q, S и P. Чтобы избежать возникновения сингулярности решений уравнений (4), следует произвести следующие замены:

й = (I + K) M_u , а = (I - K) М_ст .                         (6)

В результате оба уравнения (4) принимают идентичный вид:

2ОМ = [(гаЛ — s )( i — к) + (q + ta^-1P) (I + K)] MJ,              ( 7)

где индекс j = [u, а].

Обычно отличие упругих параметров зоны нарушения и породы вдали от скважины не превышает 20%, что позволяет применить методы теории возмущений к матричному уравнению Риккати для вычисления профиля упругих параметров зоны нарушения. Дисперсионной кривой нормальной моды в невозмущенной среде соответствуют корни уравнения (3): кц v и ш^. При заданньix величинах кг и v изменение упругих свойств волновода приведет к сдвигу корня ш^. Представим возмущенные упругие параметры среды Х^р (г), ц^р (г) и р^р (г) внутри зоны нарушения, а также возмущенное решение уравнения Риккати (1) Z^p (г) и частоты ш^р следующим образом:

ц^р (г) = ц (г) + Ац (г), Х^р (г) = Х (г) + АХ (г),              (8)

р^р (г) = р (г) + Ар (г) , Ш^р = Шг + Ашг, Z ^P (г) = Z (г) + AZ (г).

Будем считать возмущения Ац (г), АХ (г), Ар (г), Аш, и AZjj (г) малыми. Подставляя выражения (8) в матричное уравнение Риккати (1) и раскладывая его по степеням параметра малости, легко показать, что для матрицы AZ (г) в первом порядке теории возмущений получается эволюционное уравнение а^ + M1AZ + AZM2 + шг (2рАшг + шгАр) I + АцМз = 0,(9)

аг где обозначено:

М1 = ZЛ + S, М2 = ЛZ + Q,(10)

М з = Ац ^ P + ZЛ 2 Z + 2 ^цАХ ^^ц ^Q^Q 2 + ZQ 2 + Q₂Z

Ц                  (2ц + Х)2 8

1 / 1 zv гкг \               (2^+л)2   00

Q2 =     0 0   0    , Л2 = I 0     Д2

ц ' \ 0 0    0                     0      0

ц2

Матрицы Л. Q. S и P рассчитываются для среды с невозмущенными параметрами по формулам (2), а символ f означает эрмитово сопряжение. Если возмущения упругих параметров внутри неоднородного слоя являются непрерывными функциями г, то их можно представить в виде степенных рядов:

го                 п               го                 п              го                 п

Ац(г) = £щ () , АХ(г) = £> () , Ар(г) = £_7п (^)

П \ г2 - гі/                     \Г2 — гі/                     \Г2 — гі/ п=0     4         z                 п=0     4         z                 п=0     4         z

(И)

с коэффициентами а_п, З_п и у_п. Для рассматриваемых мод елей ограничимся первыми N членами разложения. Тогда уравнение (3) для возмущенной среды, выполняемое для чисел кг, v ^ и ш?, примет следующий вид:

det

Z — Z l +

дAZ дAш_г

-

ZУ Аш- + Е Е

7=qJa п=0

дAZ

деп

еп

= 0.

После ряда алгебраических преобразований сдвиг собственной частоты Ашг можно выразить через возмущения параметров слоя:

К^ ЯЬ [с (%Z. Z, Zl) еп]

D (®§ • %•Z 7

где вещественные функции С (X) и D (X) можно представить в виде линейной комбинации элементов матриц дAZ/де_n, д AZ/дАшг, д Z L/дш, Z и Zl, рассчитанных на внутренней границе неоднородного слоя т = ті. Значения производных дAZ/де_n ил и д AZ/д Ашг могут быть вычислены из решений уравнений, полученных из уравнения (9) путем его дифференцирования по е_п ил и Aшг соответственно. При их решении учитываются начальные условия в точке т = т—, согласно которым д AZ/де_n = 0, а значение дA Z /дAшг может быть найдено либо аналитически, либо численно. Значение производной д ZL/дш в точке т = ті рассчитывается через явное аналитическое выражение для матрицы Zl-

Далее описанный выше подход будет применен для расчета дисперсионных кривых изгибной моды (V = 1) и соответствующих ей волновых полей в скважинах при наличии зоны нарушения с различными упругими свойствами. Полученные кривые используются для вычисления профиля медленности поперечных волн внутри неоднородной зоны.

3.    Результаты расчетов и их обсуждение

Упругие свойства и геометрия рассматриваемых моделей представлены в табл. 1. Жидкость, заполняющая скважину, и внешняя порода однородные, а медленности продольных и поперечных волн Si (т) и St (т) внутри неоднородного слоя меняются в указанных интервалах. Плотность породы внутри данного слоя будем считать равной плотности вдали от скважины. Внутренний и внешний радиусы зоны нарушения ті и т— равны 0.1 м и 0.4 м соответственно.

Таблица!

Геометрические и упругие параметры скважины с зоной нарушения

Слои	St, мс/м	Si, мс/м	р, кг/м3	т, м
Жидкость	—	0.67	1000	[0, 0.1]
Зона нарушения	[0.97, 0.87]	[0.4, 0.36]	2000	[0.1, 0.4]
Внешняя среда	0.87	0.36	2000	[0.4, то]

Для изучения влияния типа радиальной неоднородности внутри слоя была выбрана степенная зависимость параметров Ламэ А (т) ид (т) от радиуса:

д (т)=Aц ( ^тГ + д⁰,  А (т) = AA ( ^тУ + А⁰.

V т— — П/                  V— — ті/

Величины А0, д0, A А и Aд выбирались таким образом, чтобы удовлетворить равенствам St = 0.97 мс/м, Si = 0.4 мс/м при т = ті и St = 0.87 мс/м, Si = 0.36 мс/м при т = т—. Параметр р определяет тип неоднородности упругих свойств в рассматриваемом слое. Так, при т = 0 ил и т ^ то такой слой является однородным, однако в первом случае он соответ-свует условию отсутствия зоны нарушения в скважине, а во втором характеризует ступенчатое изменение упругих свойств среды при переходе через границу г = г2. Дисперсионные кривые, вычисленные с помощью уравнений (1) - (3) при различных значениях параметра т (т = 0, 0.33, 1, 3 и то), представлены на рис. 1.

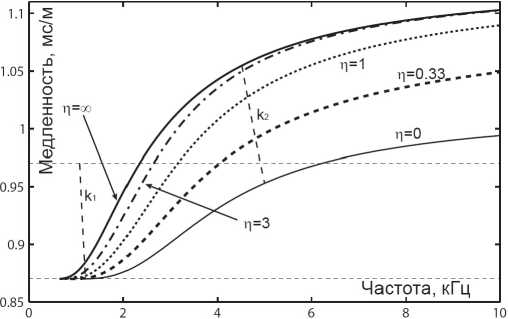
Рис. 1. Дисперсионные кривые изгибной моды в скважинах с различными неоднородными зонами нарушения

Параметры т = 0 и т ^ то соответствуют предельным случаям возможных изменений упругих параметров внутри зоны нарушения. Кривые, рассчитанные для т = 0 и т ^ то, ограничивают область, в которой располагаются кривые, построенные для остальных значений этого параметра. Наиболее сильное влияние параметра т наблюдается в области высоких и промежуточных частот. В области низких частот зависимости обладают схожим поведением и асимптотикой. Такое поведение объясняется тем, что моды в скважине сосредоточены в окрестности ее стенки. Для волн, длина которых меньше ширины зоны нарушения, скорость распространения определяется упругими параметрами среды только вблизи стенки скважины. В случае низких частот длина волны стремится к бесконечности, и зона нарушения оказывает малое влияние на скорость распространения мод по сравнению с породой вдали от скважины.

Перейдем теперь к рассмотрению влияния неоднородности зоны нарушения на радиальные профили векторных волновых полей щ (г) и а (г). Параметр не однородности т влияет на распределение напряжений внутри породы и на глубину проникновения нормальных мод, которую удобно оценить из условия зависимости энергии, переносимой модой, от радиальной координаты г. Так, радиальную зависимость суммы потенциальной и кинетической энергии упругих колебаний, приходящуюся на единицу объема среды, можно представить как функцию Гамильтона

^{Н (г)} = 2 А^(г) (^Екк ^{(г) Е}кк ^(г)) + ^ ^(г) Ең ^{(г) Е}* ^(г) + 2 р ^(г) ш²щ щ\ (15) где Eij — компоненты тензора деформации. Для расчета этого профиля, а также профиля напряжений а (г) воспользуемся формулами (4) или (7). Положим, что а_тт (гі) = 1, и рассчитаем волновые поля для значений кі и ш, принадлежащих дисперсионной кривой. Радиальные профили, вычисленные для разных значений т будем сравнивать при заданных волновых числах кі и к2, соответствующих промежуточным и низким частотам. Короткие изолинии на рис. 1 соответствуют таким значениям медленности S и частоты f, при которых волновое число к = (Sf)^-1 неизменно и равно либо кі, либо &2- Изолинии, обозначенные как кі и к2, пересекают дисперсионную кривую, вычисленную для скважины без зоны нарушения (т = 0), на частотах 1.2 кГц и 5 кГц соответственно.

На рис. 2а, 26 показаны профили атт (г) и Н (г) / max (Н (г)) при к = кі и различных значениях т- Профиль значений атт (г), вычисленный для скважины без зоны нарушения (т = 0), имеет максимум вблизи стенки скважины и затем монотонно затухает вглубь породы. При увеличении параметра т профиль атт начинает уширяться, а максимум смещается вглубь среды. Из зависимости величины Н (т) / max (Н (т)) от параметра ту, показанной на рис. 26, видно, что увеличенние у ведет к сужению профиля энергии моды. Данный факт свидетельствует об уменьшении глубины проникновения данной моды вглубь породы при усилении неоднородности породы. Максимальное отклонение полученных профилей от распределений, рассчитанных для модели с ту = 0, наблюдается в случае ту ^ то, который соответствует резкому скачку упругих свойств среды в точке т = Т2. Аналогичный анализ распределений щ,. (т) и Н (т) / max(H (т)) (см. рис. 2в, 2г), проведенный для промежуточных частот (к = к2), показывает слабое влияние параметра ту на данные профили. При этом наличие неоднородной зоны нарушения приводит к значительному изменению дисперсионных кривых.

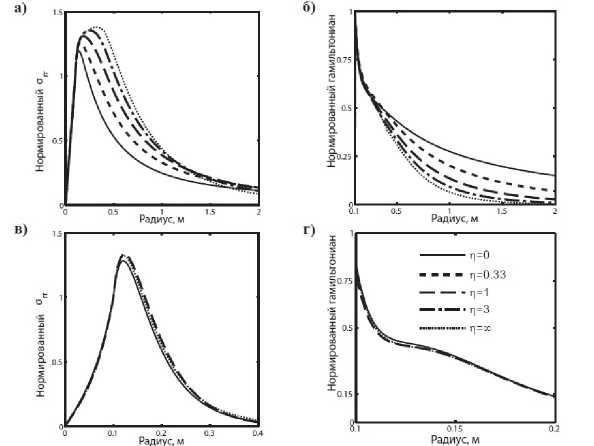
Рис. 2. Нормированные профили напряжений о_тт и функции Гамильтона Н (т), рассчитанные для волновых чисел к1 (а, б) и к₂ (в, г) в скважинах с различными типами неоднородности

Применим теперь теорию возмущений к рассмотренным моделям скважин с неоднородной зоной нарушения, для которых параметры Ламэ А (т) и ц (т) зависят от координаты т по формуле (14). Величины А⁰ и ц⁰ соответствуют скважине без зоны нарушения (невозмущенная модель). Данные параметры характеризуют упругие свойства внешней среды и могут быть найдены экспериментально. Известно, что для скважин в породах, аналогичных рассматриваемым в данной работе, вариации параметра А (т) оказывают слабое влияние на дисперсионные кривые [7]. По этой причине будем считать величину данного параметра постоянной (А (т) = А⁰) внутри зоны нарушения. Тогда только функция Ац (т) будет характеризовать возмущение упругих свойств. Дисперсионная кривая изгибной моды, рассчитанная для невозмущенной среды, показана пунктирной линией на рис. 3, а аналогичная кривая, заданная для неоднородной (возмущенной) зоны нарушения, изображена сплошной линией. Для вычисления упругих параметров этой зоны, предположим, что возмущения Ац(т) определяются разложением (11), где рассматриваются члены до N = 3.

Рассмотрим несколько точек ( к{,ш^, показанных кружками на рис. 3 и лежащих на заданной дисперсионной кривой. Для каждого к можно найти соответствующие значения частот (квадратики на рис. 3), принадлежащих кривой, рассчитанной для невозмущенной среды. Рассчитанную разность этих частот Ашц согласно уравнению (13), можно представить в виде

Аш = A1ai + А² « 2 + А3«3 . (16)

Комбинация таких уравнений, полученных для трех волновых чисел к/, кт и кп, дает систему линейных уравнений, решением которой являются коэффициенты оц, «2 и «3. Их подстановка в разложение (11) позволяет рассчитать профиль параметра р (г) или медленности St (г). Для повышения точности такие профили могут быть усреднены для всех возможных комбинаций волновых чисел кр кт и кп.

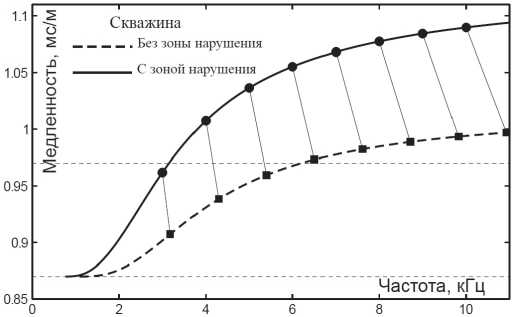
Рис. 3. Дисперсионные кривые для невозмущенной среды (пунктирная линия) и возмущенной среды (сплошная линия)

На рис. 4 показаны результаты восстановления профилей медленности S_t (г) внутри неоднородного слоя (пунктирные линии) и их сравнение с реальными моделями (сплошные линии), параметры для которых задаются формулой (14), где ц = 0.33, 1 или 3. Абсолютная ошибка St (г) не превосходит 1% для ц = 1 и 3. Для ц = 0.33 ошибка увеличивается вблизи стенки скважины, что объясняется недостаточным количеством членов, используемых в разложении (11), для аппроксимации резкого возрастания медленности. Отметим, что предложенный метод расчета упругих свойств зоны нарушения может быть реализован в рамках итерационного процесса, в котором величины, найденные на некотором шаге, используются в качестве параметров невозмущенной среды на следующем шаге.

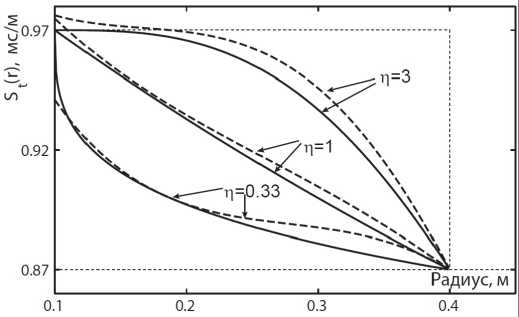
Рис. 4. Заданные (сплошная линия) и восстановленные (пунктирная линия) профили медленности поперечной волны внутри зоны нарушения

4.    Заключение

В данной работе метод матричного уравнения Риккати применен для рассмотрения влияния неоднородной зоны нарушения породы вблизи стенки скважины на дисперсионные свойства изгибной моды и соответствующие ей волновые поля. Показано значительное влияние такой зоны на положение дисперсионных кривых для длин волн, меньших или сравнимых с шириной зоны. Ее влияние также было проиллюстрировано на примере расчета радиальных профилей напряжения ст_ТТ (г) и нормированной функции Гамильтона Н (г). Так, на низких частотах наличие зоны нарушения приводит к возникновению особенностей в форме профилей ст_тт (г) и Н (г) и ведет к уменьшению глубины проникновения изгибной моды.

Для определения упругих параметров зоны нарушения использовались методы теории возмущений. Для большинства рассматриваемых моделей относительная погрешность вычисления профиля медленности поперечной волны не превысила 1%. Отметим, что описанный в данной работе подход без потери общности может быть использован и для более сложных волноводов (например, трубы, обсаженные скважины, композитные среды и т.д.).