Метод расчета гидротранспорта крупнокусковых горных пород в глинистом растворе

Экономическая эффективность применения гидротранспорта для перемещения горных пород существенно снижается с увеличением их крупности, что объясняется в первую очередь соответствующим возрастанием его энергоемкости, связанным с необходимостью обеспечения более высоких скоростей потоков гидросмесей. Кроме того, увеличивается износ гидротранспортного оборудования.

Вместе с тем, скорости гидротранспортирования горных пород и, соответственно, его энергоемкость, а также износ трубопроводов, могут быть значительно уменьшены, если в качестве несущей среды для крупнокусковых горных пород вместо воды использовать жидкости более высокой плотности и вязкости. Таковыми в условиях горных предприятий могут растворы минеральных солей, суспензии и глинистые растворы, а также органические жидкости.

На рис. 1 представлены результаты экспериментальных исследований, проведенных в промышленных условиях при гидротранспортировании дробленых полускальных пород со средней крупностью 60÷70 мм в растворах (пульпах), образованных путем гидромониторного размыва глинистых пород наносов верхнего уступа карьера.

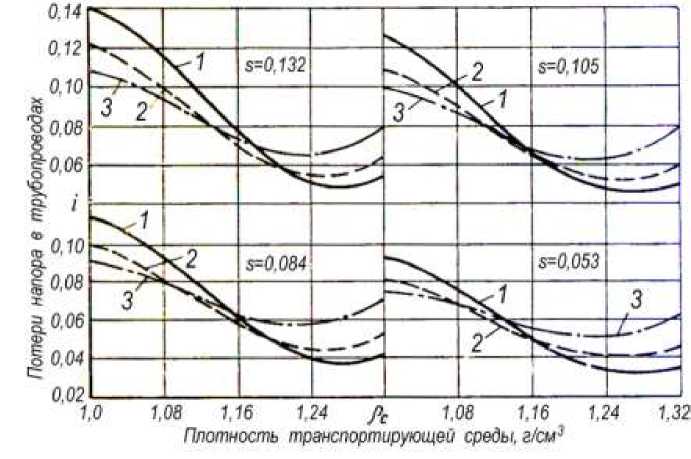
Рис. 1. Зависимости потерь напора от плотности глинистого раствора.

Измерения были выполнены на участках трубопроводов с внутренним диаметром 510, 458 и 406 мм (кривые соответственно 1 , 2 и 3 на рис. 1) при плотности глинистого раствора до 1,32 г/см³, объемной концентрации s до 16% и расходе гидросмеси 1900 м³/ч. Аналогичные измерения были выполнены при различных расходах гидросмеси в интервале от 1200 до 2200 м³/ч.

Анализ закономерностей изменения потерь напора в зависимости от плотности глинистого раствора при различных суммарных расходах гидросмесей и объемных концентрациях кускового материала, позволил заключить, что эта зависимость имеет явно выраженный минимум при плотности несущей среды 1,20÷1,28 г/см3. Положение точки минимума зависит от концентрации кускового материала в гидросмеси, диаметра трубопровода и средней скорости потока. Относительное снижение потерь напора в точках минимума по сравнению с гидротранспортом в воде тем выше, чем больше диаметр трубопровода.

Измерения в промышленных условиях были дополнены экспериментальными исследованиями на лабораторной установке (трубопровод диаметром 152 мм), что позволило расширить диапазон изученных параметров для обоснования обобщающих выводов и экспериментально определить влияние плотности несущей среды на величину критической скорости гидротранспортирования, соответствующей минимуму потерь напора в трубопроводе.

Анализ экспериментов на лабораторной установке показал, что величина критической скорости обусловлена, помимо концентрации кускового материала в гидросмеси, главным образом плотностью несущей среды. Относительное снижение критической скорости является более интенсивным при больших значениях плотности глинистого раствора. Зависимость потерь напора при критической скорости от плотности несущей среды имеет минимум при плотности в интервале 1,30―1,35. Величина потерь напора в точке минимума зависит от концентрации кускового материала в гидросмеси. В этом интервале плотности глинистого раствора критическая скорость близка к нулю при величине потерь напора не равной нулю, что свидетельствует о появлении у таких гидросмесей новых свойств, не присущих обычным грубодисперсным системам, ― способности оказывать начальное сопротивление сдвигу. Последнее, по-видимому, можно объяснить необходимостью преодоления сил, препятствующих сдвижению кускового материала, осевшего в нижней части сечения трубы. При плотности глинистых растворов выше 1,20÷1,28 г/см3 резко возрастает вязкость несущей среды. Однако, силы вязкости в данном случае проявляются главным образом через взаимодействие раствора с кусковым материалом, вызывая увеличение соответствующего коэффициента сопротивлений и уменьшение градиента скорости между кусковым материалом и транспортирующей средой, и в меньшей степени на границах потока. По-видимому, этим обстоятельством объясняется и тот факт, что, несмотря на относительно малое, по сравнению с плотностью кускового материала, увеличение плотности глинистого раствора, последний сохраняет свою транспортирующую способность при малых скоростях.

Изучение реологических свойств глинистых растворов, образованных путем гидромониторного размыва горных пород наносов, позволило их классифицировать как статически неустойчивые дисперсные системы, не оказывающие начального сопротивления сдвигу даже при относительно высокой плотности, и уверенно их отнести к категории неструктуированных суспензий.

При обобщении результатов экспериментальных исследований с целью разработки соответствующего метода расчета параметров гидротранспорта был использован известный в гидравлике принцип наложения различных видов затрат энергии с обоснованием общей структуры расчетной зависимости для определения потерь напора в следующем виде:

i _г    i _с 1 + А ,                                                        (1)

где i г и i с ― удельные потери напора при движении по трубам с одной и той же скоростью соответственно общего расхода гидросмеси и глинистого раствора (несущей жидкости для крупнокускового материала); Δ ― безразмерный параметр, характеризующий дополнительные затраты энергии, обусловленные наличием в гидросмеси кускового материала.

На основании проведенных экспериментальных исследований установлено, что для определения i с может быть использована формула Дарси-Вейсбаха в следующем виде:

- 22 0 v ²_.рс i , ^с 2 gD р0

где λ0 ― коэффициент линейных гидравлических сопротивлений при движении воды по трубам, предварительно обработанным гидросмесью, определяемый по формуле П.К. Конакова; D ― диаметр трубопровода, м; v ― скорость движения гидросмеси, м/с; g ― ускорение свободного падения, м/с2; ρс и ρ0 ― плотность соответственно глинистого раствора и воды.

Раскрывая значение параметра Δ на основе обобщенного анализа результатов выполненных экспериментов с использованием основных положений теории подобия и размерности, а также с учетом соотношения (2), исходное уравнение (1) можно представить в следующем виде:

i = - 0 v ²

^г 2 gD

рс0рс р0   р0

(n a1,5s0,5k as,

v

где a = ^{рк рс} рс

― параметр Архимеда, отображающий относительную плотность кусковых горных пород в глинистом растворе; s рг -рс рк -рс

объемная концентрация кускового материала в гидросмеси; ρ г и ρ к ― плотность соответственно гидросмеси и кусковых горных пород; k и п ― эмпирические константы.

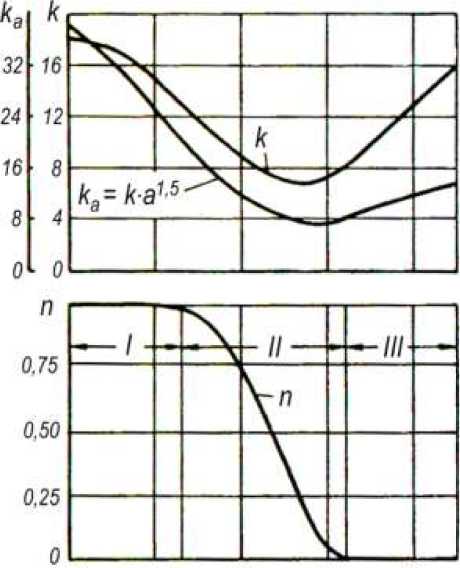
Численные значения эмпирических констант k и п зависят от плотности глинистого раствора и определяются в соответствии с графиками, представленными на рис. 2. На этом же рисунке даны значения параметра k a = ka для случая, когда по трубам перекачивается кусковатый материал плотностью ρ к = 2650 кг/м³.

1,0       1.1       1.2         1.3        1.4

Плотность транспортрующей среды г/см3

Рис. 2. Графики для определения эмпирических констант k и п .

На графике зависимости п = f (ρ с ) (см. рис. 2) можно выделить три характерные зоны:

первая зона (1 -р_с 1,16) ― показатель степени n const 1 : перенос кускового материала в глинистом растворе обусловлен в основном гидродинамическим воздействием потока и в меньшей степени проявлением сил вязкости при обтекании перемещаемых частиц потоком несущей жидкости; снижение критических скоростей по мере утяжеления глинистого раствора в этой зоне определяется в основном уменьшением параметра Архимеда; для этой зоны критическая скорость гидротранспортиров ания определяется следующим образом:

v кр - V agD ³ ks ^0,5 ;                                         (4)

вторая зона (1,16-рс 1,32) ― показатель степени п резко изменяется от 1 до 0: движение кусковых пород в потоке гидросмеси обусловлено как гидродинамическим воздействием глинистого раствора, так и силами вязкости; в этом интервале наблюдается более резкое уменьшение критических скоростей, которые определяются следующим образом:

п+2

v _кр     gD n k a ^1,5 s ^0,5     ;                                  (5)

при заданных производительности гидротранспортной системы по гидросмеси Q г (м³/с) и концентрации s кускового материала в потоке глинистого раствора величина диаметра трубопровода, соответствующая критическому режиму гидротранспортирования, определяется по формуле

D _кр

16 Q г ²

1 ;

2g n k 1,5 0,5 n 2 gn k a s для определения удельных потерь напора при критических режимах гидротранспортирования может быть использована формула n 2   0v2 с iг.кр                        ;                                                  (7)

n   2 gD р0

третья зона |6с  1,32  ― показатель степени n const 0 : с увеличением плотности глинистого раствора коэффициент k возрастает; по-видимому в этой зоне транспортирование кусковатого материала связано в значительной мере с проявлением вязкопластичных свойств несущей среды (глинистых растворов).

При рс  1,32 понятие vкр как скорости, обеспечивающей минимум потерь напора теряет смысл, так как функция iг  f (v) имеет минимум при v = 0. Величина потерь напора, соответствующая моменту начала движения гидросмеси в трубопроводе, определяется выражением i= х0рс      1,5 0,5

.

г      as р0

Для определения потерь напора при гидротранспортировании крупнокусковых горных пород в глинистых растворах могут быть использованы графики, представленные на рис. 3, где в логарифмических координатах представлена зависимость безразмерного комплекса iгiv

.

г с в функции параметра Фруда Fr iс bgD

Определив по графикам рис. 3 величину параметра ψ при известном численном значении параметра Фруда, потери напора в трубопроводе рассчитывают по формуле iг   iс 1 +b•V ,(9)

где ic определяют в соответствии с приведенным выше уравнением Дарси-Вейсбаха, а параметр b ― по формуле b   a1,5 s0,5.(10)

Для определения критических скоростей можно пользоваться таблицей 1, в которой даны критические значения параметров Фруда при различной плотности глинистых растворов и концентрации s крупнокусковых горных пород в гидросмеси.

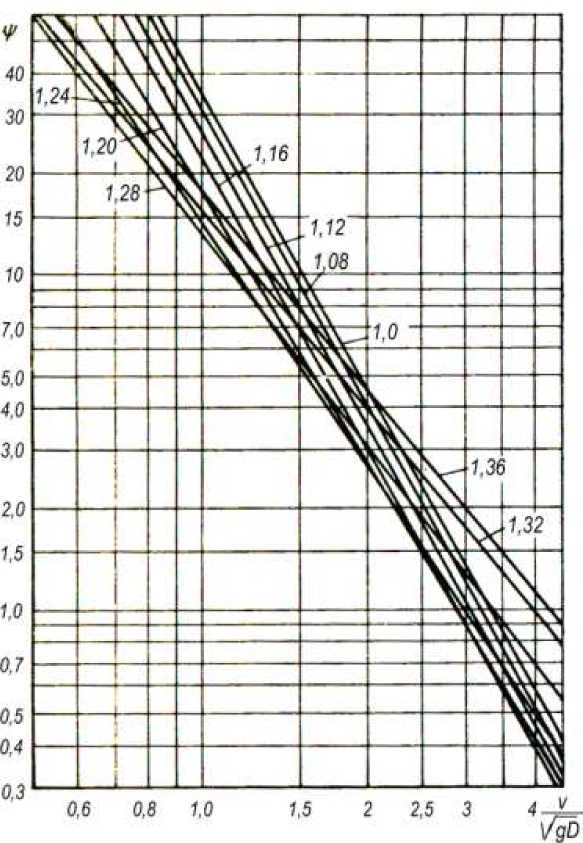
Рис. 3. Графики зависимостей ψ = f ( Fr ) при различной плотности глинистого раствора

Для определения потерь напора при критических режимах гидротранспортирования можно пользоваться формулой in+

iг.кр              iс.кр , где iс.кр ― потери напора при перемещении по трубам глинистого раствора, определяемые по формуле (2) для критического режима; п ― показатель, определяемый по соответствующему графику (рис. 2).

Оптимальные параметры гидротранспортирования могут быть определены из условия обеспечения минимума энергетических затрат на перемещение крупнокусковых горных пород и подачу глинистого раствора в пульпосмесительный узел, так как все остальные затраты изменяются пропорционально мощности транспортных агрегатов.

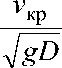
Критические значения параметров Фруда

Таблица 1.

s	Плотность глинистого раствора, г/см3
	1,0	1,04	1,08	1,12	1,16	1,20	1,24	1,28	1,32
0,091	2,26	2,17	2,05	1,89	1,70	1,44	1,08	0,60	0,109
0,100	2,30	2,21	2,08	1,92	1,72	1,46	1,10	0,61	0,112
0,111	2,34	2,25	2,12	1,95	1,75	1,49	1,11	0,62	0,115
0,125	2,38	2,29	2,16	1,99	1,78	1,52	1,15	0,64	0,118
0,143	2,44	2,34	2,21	2,04	1,82	1,56	1,18	0,66	0,122
0,167	2,50	2,40	2,26	2,09	1,87	1,60	1,22	0,68	0,127
0,200	2,58	2,48	2,33	2,15	1,93	1,66	1,27	0,71	0,134