Метод расчета электромагнитного момента для задач конечно-элементного моделирования асинхронного двигателя

Дальнейшее развитие теории электрических машин сложно представить без разработки комплексных математических моделей, максимально использующих возможности современной вычислительной техники. На кафедре электроники и микроэлектроники Магнитогорского государственного технического университета ведутся работы в одном из таких направлений. Речь идет о разработке конечно-элементных математических моделей асинхронных двигателей с короткозамкнутым ротором. Метод конечных элементов [1-5] находит все большее применение при расчете электротехнических устройств благодаря высокому уровню приближения математической модели к объекту исследования на уровне физики протекающих в нем электромагнитных, электромеханических и тепловых процессов. Фактически данный уровень приближения ограничивается только возможностями используемой компьютерной техники. Так, в частности, при моделировании асинхронных двигателей, метод конечных элементов позволяет точно учитывать геометрию машины в ее поперечном сечении, а также электрические параметры двигателя, включая нелинейность кривой намагничивания, сопротивление стержней и соединительных колец ротора и другие особенности, как например, возможные дефекты в магнитной и витковой системе электрической машины.

Фундаментальную роль в преобразовании энергии электромагнитного поля двигателя в механическую энергию вращения ротора играет электромагнитный момент. В задачах численного анализа электрических машин для вычисления сил и моментов наибольшее распространение получили методы, основанные на интегрировании так называемого тензора напряжения Максвелла (Maxwell’s stress tensor) [4-6].

Рассмотрим ротор двигателя и замкнутую поверхность S, окружающую ротор (рис. 1). Используя тензор напряжения Максвелла, можно получить выражение для элементарной силы, действующей со стороны магнитного поля:

dF = — 5-и S--—S²n,         (1)

Ц(Д )   2ц0

где п - вектор единичной нормали к поверхности S.

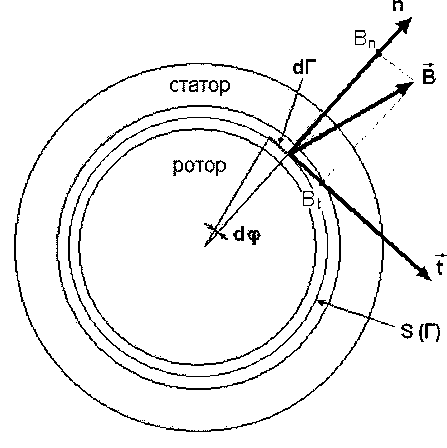
Рис. 1. Поперечное сечение двигателя и поверхность интегрирования S

Поскольку поле в поперечном сечении двигателя обычно принимается плоскопараллельным, то вектор магнитной индукции можно представить двумя ортогональными составляющими:

В = В_п и+ B_t t ,                            (2)

где В_п - составляющая, нормальная к поверхности 8; В, - составляющая, тангенциальная к поверхности 8; t - вектор единичной касательной к поверхности S.

Подставив (2) в (1), получим:

dF=— [В^-В^п--B_nB_tt.      (3)

2ц0V 7 Мо

Момент, действующий на ротор со стороны магнитного поля, может быть выражен интегралом по поверхности S следующим образом:

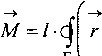
-—вл"

. Но

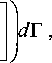
где / - длина активного пространства двигателя.

Подставив в (б) следующие выражения:

гх /

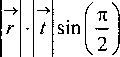
^Dr ⁺^5

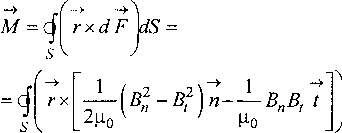
dS, (4)

где г - радиус-вектор точки, лежащей на поверхности S.

Поскольку нормальная составляющая силы не участвует в создании вращающего момента, то выражение (4) можно упростить:

S

гх ——B_nB_t t dS.

Принимая допущение о плоскопараллельно-сти поля внутри двигателя, интеграл по поверхности S можно заменить криволинейным интегралом по замкнутому контуру Г, в который вырождается поверхность S:

получим:

Цог+1Л2 Ч м =--V; М \ВПВ^,         (7)

4^о о где Dr - диаметр ротора; /б - ширина воздушного зазора.

Возвращаясь к методу конечных элементов, рассмотрим приведенный на рис. 2 фрагмент сетки конечных элементов расчетной области поперечного сечения двигателя в области воздушного зазора. Сетка состоит из трех слоев, образованных треугольными конечными элементами.

Используя рис. 2, формулу (7) для вычисления электромагнитного момента можно приближенно записать в виде

4ЦО м 2         % V 7

где В_пЛ и В_и- соответственно нормальная и тангенциальная, относительно контура интегрирования Г, составляющие вектора магнитной индукции в центре масс z-го конечного элемента среднего слоя сетки воздушного зазора двигателя;

N - число конечных элементов в среднем слое сетки воздушного зазора.

Купцов В.В., Петушков М.Ю., Сарваров А.С.

Метод расчета электромагнитного момента для задач конечно-элементного моделирования...

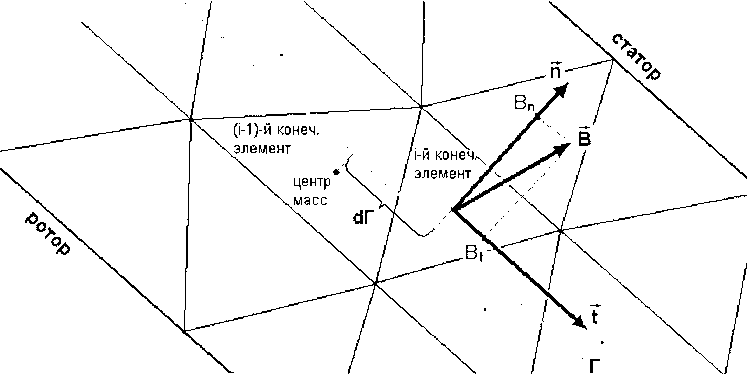
Рис. 2. Пояснение к расчету электромагнитного момента

В формуле (8) используется среднее между двумя соседними конечными элементами значение произведения В_п В,.

В работе [7] изложена методика косвенного определения моментов на валу АД, согласно которой момент АД определится как:

ea =Ua 'R еь = иь-Ч R

•^а=-[^еа^                    (9)

Мэ- = ^-p\NVa-ib-^b-iaY где R - активное сопротивление обмотки статора; р - число пар полюсов асинхронного двигателя; иа, ub, ia, ib, еа, еь, \уа, хуь,- мгновенные значения фазных напряжений, токов, э.д.с. и потокосцепления соответственно; Мэ.. - электромагнитный момент асинхронного двигателя.

На рис. 3 представлена кривая электромагнитного момента, рассчитанного через тензор напряжения Максвелла по формуле (8), полученная при моделировании прямого пуска АД. По результатам моделирования была получена еще одна кривая электромагнитного момента АД, рассчитанного косвенным методом по формулам (9).

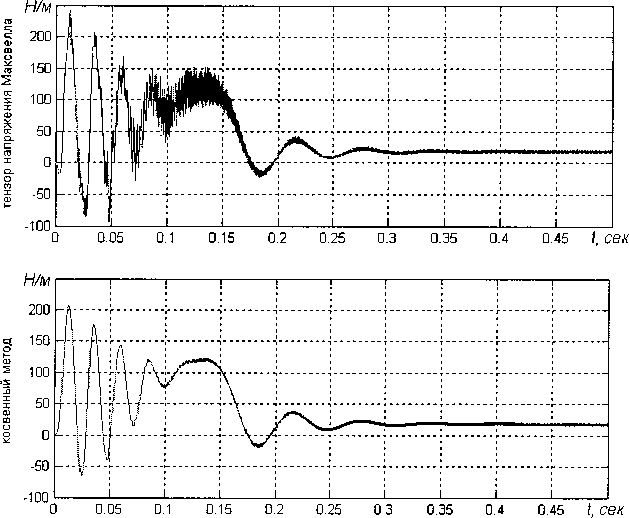
Рис. 3. Сравнение кривых электромагнитного момента пуска АД, рассчитанных двумя методами