Метод расчета надежности функциональных систем самолетов гражданской авиации по статистическим материалам эксплуатантов

Статистические материалы эксплуатантов (авиакомпаний, регионов и отрасли гражданской авиации в целом) [1; 2], а также зарубежной авиационной техники [3] убедительно показывают, что средний налет на отказ самолетов в целом, их функциональных систем и отдельных агрегатов для конкретных типов самолетов не зависит от времени (от налета часов самолетов). Постоянство среднего налета на отказ обеспечивается реализацией программ технического обслуживания самолетов, направленных на поддержание уровня летной годности, т. е. надежности агрегатов, систем и самолетов в целом.

Принятый в расчетах надежности функциональных систем метод основывается на теореме умножения вероятностей. В соответствии с ней вероятность безотказной работы последовательно соединенных агрегатов принимается равной произведению вероятностей безотказной работы этих агрегатов. Вероятность отказа параллельно включенных агрегатов определяется в виде произведения вероятностей их отказа.

Сложные функциональные системы содержат большое число агрегатов и имеют многократное общее и индивидуальное резервирование отдельных агрегатов. В связи с этим расчетные зависимости для вероятности отказа либо безотказной работы систем содержат суммы вероятностей отказа агрегатов, суммы их степеней и произведений.

Центральная предельная теорема теории вероятностей [4] утверждает, что распределение вероятности суммы случайных величин неограниченно приближается к нормальному закону распределения при неограниченном увеличении числа слагаемых. В функциональных системах самолетов число агрегатов достаточно велико, но, естественно, ограниченно.

Рассмотрим вид интегральной функции распределения отказа системы и ее плотности вероятности на примере расчета тестовой системы. Пусть система имеет 4-кратное общее резервирование ветви содержащей 4 последовательно соединенных агрегата. Положим, что параметр потока отказа является одинаковым для всех агрегатов и равным 1 • 10 4.

В отраслевой нормали «Надежность изделий авиационной техники» [5] для малых, свойственных агрегатам авиационной техники, значений параметра потока отказов предложено распределение вероятностей отказа агрегатов представить законом равномерной плотности вероятности, т. е.

О() = ^ /. (1)

Следует отметить, что распределение (1) при малых вероятностях Q(t) хорошо согласуется с экспоненциальным распределением.

При этих предположениях вероятность отказа тестовой системы определяется в виде

^ ) 11 (1 1 • 10 4t)4|4. (2)

Рассчитанная по формуле (2) функция вероятности отказа системы приведена на рис. 1. Там же представлена аналогичная зависимость, но построенная в предположении экспоненциального закона распределения вероятности отказа агрегатов.

Вероятность отказа систем авиационной техники нормируется Нормами летной годности самолетов [5] в виде вероятности отказа на 1ч полета, приводящего к последствиям различной степени тяжести. Для рассматриваемой системы эти зависимости приведены на рис. 2. Характер изменения во времени функции распределения вероятности отказа системы (рис. 1) и вероятности ее отказа на1ч полета близки к интегральной функции распределения вероятности и плотности вероятности нормального распределения.

Здесь следует иметь в виду, что плотность вероятности определяется по формуле f (t ) = d^. (3) а вероятность отказа на 1ч полета в виде

Q ic ( t ) =^ Q^ ■ (⁴)

Поскольку At = 1 ч, а t изменяется в пределах десятков тысяч часов, допустимо считать At величиной 4-го порядка малости. Но тогда зависимости^) и Q_c1(t) мало чем отличаются друг от друга.

При использовании закона распределения с равномерной плотностью вероятности (1) плотность вероятности равна

, , dQ ( t)

f (t ) = —— = ® = const, (5) dt т. е. в этом случае плотность вероятности и параметр потока отказов тождественны. Тогда, приняв за единицу времени 1 ч, допустимо считать, что параметр потока отказов есть не что иное, как вероятность отказа на 1 ч.

Таким образом, рассматриваемая тестовая система содержит агрегаты, вероятность отказа которых в течение 1 ч не зависит от времени. Естественным было бы ожидать независимость от времени и вероятности отказа системы на 1 ч. Эти представления расходятся с результатом расчета системы, представленном на рис. 2.

В рассмотренной методике задача расчета надежности решена относительно интегральной функции распределения вероятности отказа системы, а вероятность отка- за на 1ч определена как производная от нее. При построении интегральной функции распределения в рассмотрение введено время t, которое затем возводится в степени и суммируется многократно в зависимости от сложности системы. При этом остается проигнорированным факт независимости от времени вероятности отказа агрегата на единицу времени.

Ниже предлагается альтернативный методологический подход к построению расчета надежности системы. При этом на первом этапе рассматривается задача расчета вероятности отказа системы на 1ч полета, а функция распределения вероятности отказа находится как результат ее интегрирования.

Рассматривается тестовая система, состоящая из и агрегатов и имеющая т кратное общее резервирование. Вероятности отказов агрегатов приняты одинаковыми и

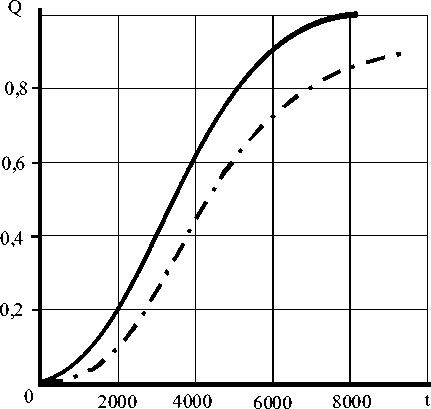
Рис. 1 Вероятность отказа системы ^^^^^^ общее резервирование — - — - ■ общее резервирование при экспоненциальном распределении

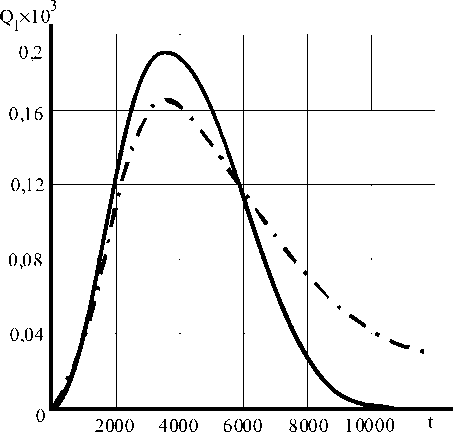
Рис. 2 Вероятность отказа системы на 1 ч полета ^^^^^^_ общее резервирование

— , — , — общее резервирование при экспоненциальном распределении распределенными по закону равномерной плотности вероятности. Вводится понятие суммарного потока отказов системы щс, определяемого суммой потоков отказов агрегатов. Поскольку агрегатов и, а их параметры пока отказов щ одинаковы, то

Щс = и щ.

Реализация отказа с параметром потока Щс не отождествляется с отказом системы и не идентифицируется с метом его возникновения.

Необходимым и достаточным условием отказа системы в течении 1 ч является реализация в каждой из т резервированных подсистем с последовательным соединение и/т агрегатов хотя бы одного отказа. Вероятность возникновения в одной из т подсистем отказа одного агрегата в т раз меньше, чем в системе в целом. Поскольку подсистем т, то вероятность отказа одного агрегата в каждой из них в т2раз меньше. С другой стороны, вероятность одновременной реализации т независимых отка зов равна произведению вероятности этих отказов.

Поскольку вероятность отказа агрегатов принята распределенной по закону равномерной плотности вероят ности, допустимо считать вероятность реализации отказа одного агрегата в системе равной to . Тогда вероятность отказа системы в течение 1 ч определится в виде

m о = Щс-Q с1      2

m ²

m

( n ‘Щ )

2 m ²

.

Это значение вероятности отказа на 1ч полета не зависит от времени, а интегральная функция распределения вероятности отказов системы ^ является линейной функцией времени

Q с =

m

О^ЩЬ

• 2 t .

m ²

Для рассмотренной выше системы из 16-ти агрегатов вероятность отказа на 1ч будет равна qс1             =163 -®4.              (9)

В рассматриваемом числовом примере при традиционной методике расчета и щ = 10 4 вероятность отказа на 1 ч полета на отрезке времени (0,1) составляет 0,256 - 10 |3, среднее значение в интервале от0до 1 000 ч оставляет0,14 - 10 4и максимальное значение, достигаемое при t = 3 500 ч, составляет 0,18 - 10 3. При предло женном альтернативном решении задачи вероятность отказа на 1ч полета равна 0,409 6 - 10 12 и не зависит от наработки часов.

Значение интегральной функции распределение вероятности отказа системы в первом случае равно 1 при t = 10 000 ч, во втором случае при этой же наработке часов оно составляет 0,409 6 - 10 8.