Метод расчета параметров точности изготовления колес с многопериодными дорожками планетарных шариковых передач

РЕФЕРАТ

МЕТОД РАСЧЕТА, ПАРАМЕТРЫ ТОЧНОСТИ, КОЛЕСО, МНОГОПЕРИОДНАЯ ДОРОЖКА, ПЛАНЕТАРНАЯ ШАРИКОВАЯ ПЕРЕДАЧА, ПОГРЕШНОСТИ ОБРАБОТКИ

Точность изготовления колес с многопериодными дорожками значительно влияет на плавность работы и нагрузочную способность планетарной шариковой передачи. Актуальной задачей является определение погрешностей изготовления колеса передачи.

Рассмотрен метод расчета, позволяющий определять погрешности положения обрабатываемого профиля относительно базовой поверхности детали для линейных размеров. Его можно использовать для обработки заготовок на металлорежущих станках в обычных производственных условиях.

На основе известных математических зависимостей разработан метод расчета погрешностей изготовления колеса с многопериодной дорожкой. Метод заключается в определении случайных и систематических погрешностей, связанных с различными технологическими факторами, расчете и суммировании этих погрешностей с использованием законов распределения случайных величин теории вероятности и разработанных компьютерных программ. На основе разработанного метода выведены формулы расчета суммарной погрешности обработки колеса с многопериодной дорожкой, характеризующие смещение заготовки вдоль координатных осей станка. Для определения погрешностей от смещений и поворотов деталей с многопериодными дорожками разработана методика расчета,

CALCULATION METHOD, ACCURACY PARAMETERS, WHEEL, MULTI-PERIOD TRACK, PLANETARY BALL GEAR, PROCESSING ERRORSD

The precision of manufacturing wheels with multi-period tracks significantly affects the smoothness of operation and the load capacity of the planetary ball gear. An urgent task is to determine the manufacturing errors of the transmission wheel.

The article discusses a calculation method that allows to determine the position errors of the processed profile relative to the base surface of the part for linear dimensions. It can be used for processing workpieces on metal-cutting machines in normal production conditions.

On the basis of known mathematical dependencies, a method for calculating manufacturing errors of a wheel with a multi-period track has been developed. The method consists in determining random and systematic errors associated with various technological factors, calculating and summing these errors using the laws of distribution of random variables of probability theory and developed computer programs. Based on the developed method, formulas for calculating the total error of processing a wheel with a multi-period track are derived, characterizing the displacement of the workpiece along the coordinate axes of the machine. To determine the errors from displacements and rotations of parts with multiperiod tracks, a calculation method based on the use of the matrix method has been developed.

Graphs are presented that characterize the influence of the shape error of the base surface of the wheel blank on the total processing error of the основанная на применении матричного метода.

Представлены графики, характеризующие влияние погрешности формы базовой поверхности заготовки колеса на суммарную погрешность обработки многопериодной дорожки. Предложена оптимизация режимов обработки, снижающая и стабилизирующая силу резания. Представлена диаграмма наибольших значений суммарной погрешности обработки колеса с многопериодной дорожкой.

multi-period track. Optimization of processing modes, reducing and stabilizing the cutting force, is proposed. A diagram of the largest values of the total error of processing a wheel with a multi-period track is presented.

Объектом исследования является колесо с многопериодной дорожкой планетарной шариковой передачи, которая имеет небольшие массогабаритные характеристики, большие передаточные отношения в одной ступени, технологичную конструкцию [1 – 4]. На основе этой передачи можно построить многоступенчатые передаточные механизмы, используя модульный принцип сборки. Передачи данного типа используются в редуцирующих механизмах технологического оборудования машиностроительного производства. На рисунке 1 показана схема зацепления планетарной шариковой передачи.

На рисунке 1 показан входной вал 2 с отвер-

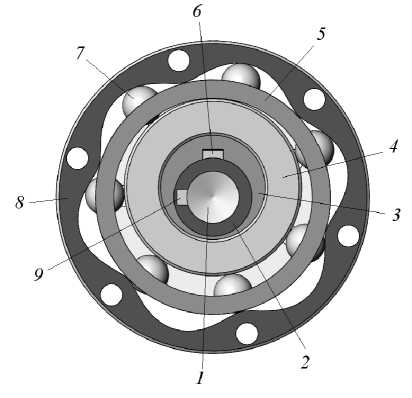
Рисунок 1 – Схема зацепления планетарной шариковой передачи стием 1 и шпонкой 9 для соединения с приводом, эксцентрик 3 со шпонкой 6 и кольцо 4 ведущего звена; водило 5 и шары-сателлиты 7 ведомого звена; колесо 8 с многопериодной дорожкой неподвижного звена. При вращении ведущего звена, установленного эксцентрично, шары-сателлиты 7 обкатываются по однопериодной и многопериодной дорожкам кольца 4 и колеса 8 и передают вращение на водило 5, связанное с выходным валом передачи.

Актуальность исследований заключается в следующем. Точность изготовления поверхности многопериодной дорожки значительно влияет на плавность работы передачи, ее нагрузочную способность и ресурс работы. Для управления точностью при проектировании планетарных шариковых передач необходимо определить погрешности деталей, возникающие при изготовлении. Для этих передач не разработаны стандартные допуски на изготовление наиболее ответственной детали – колеса с многопериодной дорожкой. Поэтому актуальной задачей является разработка методов, позволяющих рассчитывать точность изготовления многопериодной дорожки при проектировании технологических процессов.

Целью исследования является разработка метода расчета погрешностей изготовления колес с многопериодными дорожками планетарных шариковых передач с определением случайных и систематических погрешностей, а также методики расчета, основанной на применении матричного метода, учитывающей смещения и повороты деталей с многопериодными дорожками при обработке на станке.

На основе математических зависимостей, представленных в [5], разработан метод расчета погрешностей изготовления наиболее ответственной детали передачи – колеса с многопериодной дорожкой. Метод заключается в определении случайных и систематических погрешностей, связанных с различными технологическими факторами, возникающими при изготовлении деталей, расчете и суммировании этих погрешностей с использованием законов распределения случайных величин теории вероятности и разработанных компьютерных программ в среде VBA Excel.

Точность параметра (размера, отклонения формы, расположения поверхностей) при изготовлении любой детали можно определить суммированием факторов, учитываемых при анализе исследуемого параметра.

Исследуемый параметр детали Y можно представить в виде функции нескольких переменных X n где K – коэффициент относительного рассеяния выходного параметра, корректирует суммарную погрешность для заданной гарантированной надежности; n – число параметров; i – индекс элементарной погрешности; i, j – индексы погрешностей с вероятностной связью, рассматриваемые попарно; Ki, Kj – коэффициенты относительного рассеяния входного параметра; Si, Sj – абсолютная чувствительность функции цепи к изменению параметра или коэффициенты влияния, передаточные отношения; Ti, Tj – допуски параметров.

При этом коэффициент относительного рассеяния входного параметра K _i характеризует отношение поля рассеяния погрешности при нормальном законе распределения к действительному полю рассеяния. Если элементарные погрешности, изменяющиеся во времени t , являются случайными функциями времени (например, погрешность, связанная с износом инструмента), то суммарная погрешность обработки определяется по формуле

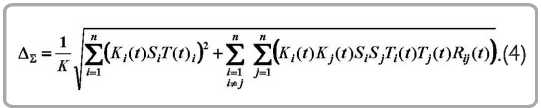
# = 4y₁,...,^X) .       (1)

После изготовления деталей реальные зна чения параметров отличаются от идеальных (но-        Если принять независимость элементарных минальных) на абсолютную погрешность            погрешностей и не учитывать их изменения во времени (оценивать конечное значение погрешностей), то при расчетах можно принять Si = 1. Тогда суммарную погрешность обработки можно рассчитать по формуле

A-^"^) ,         (2)

где Δ _i – абсолютная погрешность параметра после изготовления; X _i – реальное значение параметра; X ₀ – номинальное значение параметра.

При вероятностном методе расчёта параметры Y , Δ _i являются случайными величинами.

Согласно [5, 6], если между погрешностями, рассматриваемыми попарно, существует вероятностная связь с коэффициентом корреляции R _ij , то суммарная погрешность обработки определяется по формуле

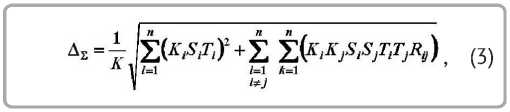
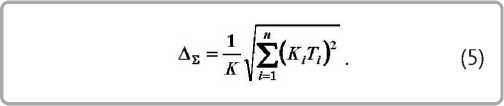
Приведенный метод расчета позволяет определять погрешности положения обрабатываемого профиля относительно базовой поверхности детали для линейных размеров. По рекомендации [5] формулу (5) можно использовать для обработки заготовок на металлорежущих станках в обычных производственных условиях.

На основе рассмотренного выше метода разработаны формулы расчета суммарной погрешности обработки колеса с многопериодной дорожкой, характеризующие смещение заготовки вдоль координатных осей станка. Формула расчета при независимых элементарных технологических погрешностях без учета их изменения во времени:

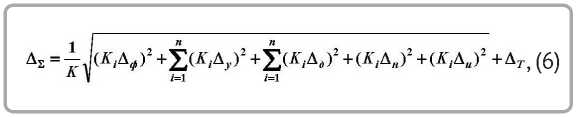
где Δ _ô – погрешность формы установочной поверхности заготовки; Δ _ó – погрешность установки, учитывающая точность базирования, закрепления заготовки, приспособления и его установки на станке; Δ _д – погрешность от упругих деформаций, учитывающая деформации станка и инструмента; Δ _í – погрешность настройки станка; Δ _è – погрешность от износа режущего инструмента; Δ _Ò – погрешность от температурной деформации технологической системы.

Формула расчета суммарной погрешности обработки при независимых элементарных погрешностях с изменением во времени отдельных параметров:

При обработке заготовки могут быть не только смещены, но и повернуты в системе координат станка. Для определения погрешностей от смещений и поворотов деталей с многопериодными дорожками разработана методика расчета, основанная на применении матричного метода.

Для определения точности положения деталей в пространстве необходимо рассмотреть смещения и повороты системы координат детали в неподвижной базовой системе координат станка [7]. Выберем системы координат: X ₀ Y ₀ Z ₀ – базовая система координат станка; x ₁₀ y ₁₀ z ₁₀ – базовая система координат, перенесенная в точку Î _{1 .} Система координат обрабатываемой детали x _1i y _1i z _1i , при поворотах на угол α – x ₁₁ y ₁₁ z ₁₁ , на угол β – x ₁₂ y ₁₂ z ₁₂ , на угол γ – x ₁₃ y ₁₃ z ₁₃ .

На рисунке 2 показана схема положения колеса с многопериодной дорожкой планетарной передачи в заданных системах координат в соответствии с [7].

Если известны значения координат a , b , c вектора смещения r и значения координат α , β , γ (углов) вектора поворота φ в системе координат

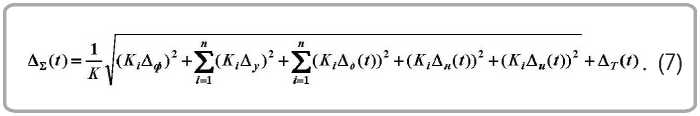
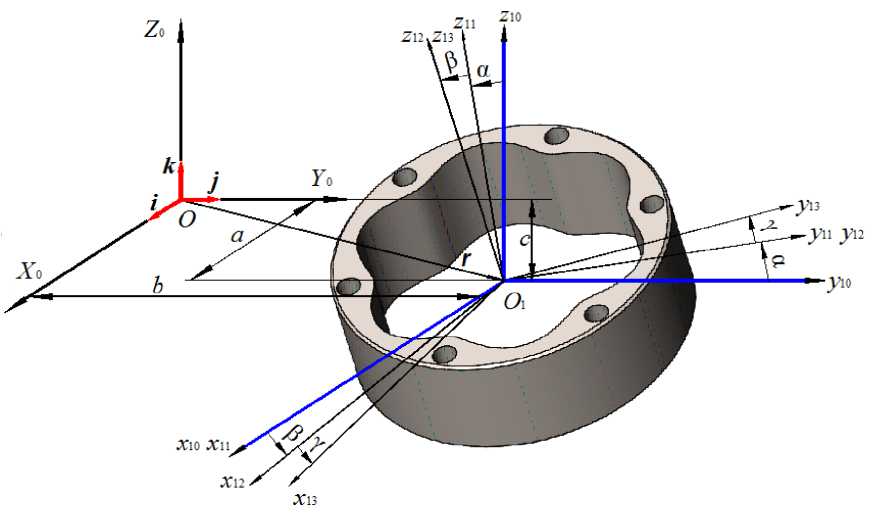
Рисунок 2 – Схема положения колеса с многопериодной дорожкой планетарной передачи

X ₀ Y ₀ Z ₀ , то можно определить координаты любой точки детали в системе координат x _1i y _1i z _1i по ее координатам в системе X ₀ Y ₀ Z ₀ и наоборот. Для этого нужно построить матрицу преобразования пространства.

При повороте системы координат x ₁₀ y ₁₀ z ₁₀ на угол α относительно оси x ₁₀ в положительном направлении (против часовой стрелки) матрица A поворота будет иметь вид:

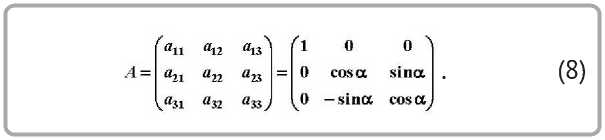
Элементы этой матрицы представляют собой проекции единичных векторов i , j , k осей координат x ₁₀ y ₁₀ z ₁₀ на оси координат x ₁₁ y ₁₁ z ₁₁ (рисунок 2).

Если известны координаты x _0N , y _0N , z _0N некоторой точки N детали в системе координат X ₀ Y ₀ Z ₀ , то в системе координат x _1i y _1i z _1i координаты этой точки x _1N , y _1N , z _1N можно определить, умножив координаты x _0N , y _0N , z _0N на элементы матрицы A , расположенные в соответствующих строках. С учетом координат начала a , b , c получим

,

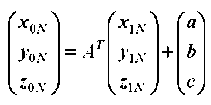
где A^T – транспонированная матрица.

Можно получить матрицы B и C , если система координат x ₁₀ y ₁₀ z ₁₀ повернута на угол β относительно оси y ₁₀ и на угол γ вокруг оси z ₁₀ в положительном направлении.

Если система координат x ₁₀ y ₁₀ z ₁₀ повернута на углы α , β , γ , то матрица K результирующего преобразования может быть представлена произведением матриц A , B , C :

< cos p cos у   sinasinpcosy+ cosasiny

К = —cospsiny — sinasinpsiny + cosacosy

— sinacosp

— cos a sinp cos у + sina siny' cos asinp siny + sinacos у   . (14)

cos a cos p        ,

Полученные матрицы преобразования пространства позволяют определить координаты любой точки N детали передачи.

Рассмотренный матричный метод можно использовать для расчета погрешностей обработки, возникающих вследствие поворотов заготовки относительно системы координат станка

■^liV — (^OiV «^ll+^O^V ^O^iz+t^ow ^^13 , (9)

при ее базировании, закреплении, а также из-за геометрических неточностей приспособлений и станков.

Если система координат детали x ₁₀ y ₁₀ z ₁₀ смещена и повернута относительно базовой си-

J’l.V = (Xo/V - й)й21 * (Лл^ - ^)^22 + (^ - C)ti23 , (10)

стемы координат X ₀ Y ₀ Z ₀ , то погрешности положения детали Δx ₀ Δy ₀ Δz ₀ относительно осей X ₀ , Y ₀ , Z ₀ после преобразования могут быть определены по формуле, учитывая (13) и (14):

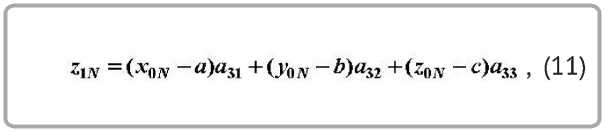
или, используя матричную запись

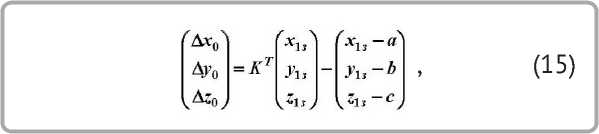
^jV -Й .VfljV-A

,

< гий

^оя —c

Координаты x _0N , y _0N , z _0N точки N в системе координат X ₀ Y ₀ Z ₀ по ее координатам x _1N , y _1N , z _1N определяются по формуле

где x _1з , y _1з , z _1з – координаты точек обрабатываемой поверхности заготовки; K^T – транспонированная матрица.

Координаты точек профиля обрабатываемой криволинейной поверхности многопериодной дорожки определяются по формулам смещенной окружности [1]:

Лп = ^х^2"" А1 $т2(;ф) + Лсо$(;ф)^ со$ф ,       (16) где р - радиус-вектор точки кривой; R - радиус окружности; А - величина смещения окружности, амплитуда многопериодной кривой; z - число периодов кривой; ф - полярный угол; Из -толщина обрабатываемой детали.

Суммарная погрешность обработки в торцовой плоскости детали

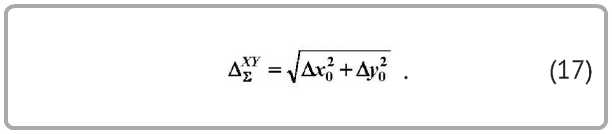
Суммарная погрешность обработки детали с учетом ее расположения в пространстве

.

В таблице 1 показаны исходные данные для расчета суммарной погрешности чистовой обработки фрезерованием многопериодной дорожки колеса исследуемой планетарной шариковой передачи.

На рисунке 3 показана диаграмма наибольших значений суммарной погрешности, учитывающей смещение и повороты заготовки при обработке на станке, рассчитанной по приведенным выше формулам.

На рисунке 3 обозначены следующие параметры: X c , Y c , Z c - наибольшие суммарные погрешности обработки, учитывающие смещение заготовки, вдоль координатных осей станка X 0 Y 0 Z 0 ; X c _n , Y c _n , Z c _n - наибольшие суммарные погрешности обработки, учитывающие смещение и повороты заготовки, вдоль координатных осей станка X 0 Y 0 Z 0 ; XY c _n , XYZ _cn - наибольшие суммарные погрешности обработки, учитывающие смещение и повороты заготовки в плоскости X 0 Y 0 и в пространстве X 0 Y 0 Z 0 . Погрешности на диаграмме можно рассматривать как отклонения формы и расположения заданного профиля дорожки на плоскости и в пространстве в системе координат станка.

Таблица 1 – Исходные данные для расчета суммарной погрешности обработки фрезерованием многопериодной дорожки
Название параметра	Обозначение	Значение
Погрешность формы базовой поверхности заготовки	^ф	0,016 мм
Погрешность установки заготовки	Δ У	0,05 мм
Погрешность от упругих деформаций станка и инструмента	Δ д	0,042 мм
Погрешность настройки станка	Д н	0,01 мм
Погрешность от износа инструмента	Д и	0,021 мм
Погрешность от температурных деформаций технологической системы	^ Т	0,15 ΔΣ
Средний радиус дорожки	R	41,5 мм
Амплитуда дорожки	A	3,75 мм
Радиус шара-сателлита	r ш	7,5 мм
Суммарный угол поворота вокруг оси X 0	α	0,00103 рад
Суммарный угол поворота вокруг оси Y 0	β	0,00103 рад
Суммарный угол поворота вокруг оси Z 0	γ	0

При фрезеровании многопериодной дорожки заготовка колеса базируется в приспособлении на станке по наружной цилиндрической поверхности и торцу. Погрешность формы базовой цилиндрической поверхности заготовки (отклонение от круглости), полученная на предыдущей технологической операции, имеет соотношение с допуском на размер в соответствии с установленными уровнями геометрической точности [7, 8]. После черновой обработки этот допуск может превышать все остальные технологические погрешности. На рисунке 4 показаны графики, характеризующие влияние погрешности формы цилиндрической поверхности заготовки на сум-

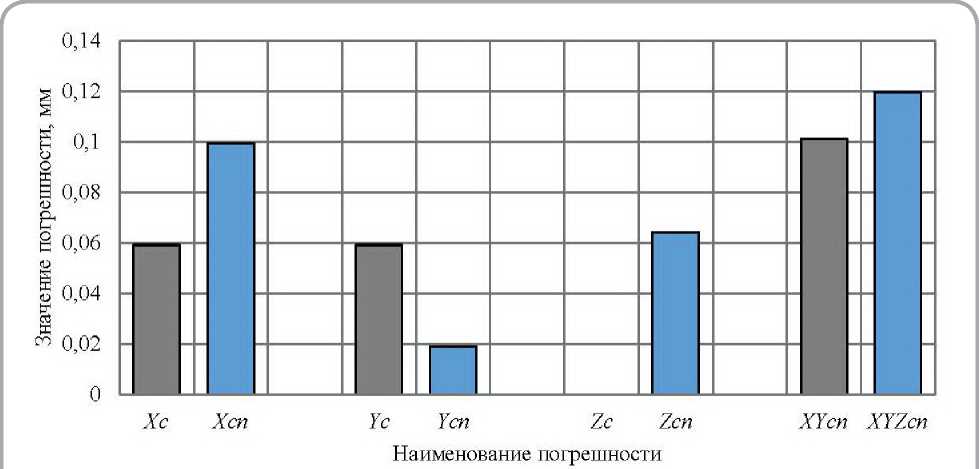
Рисунок 3 – Диаграмма значений суммарной погрешности обработки

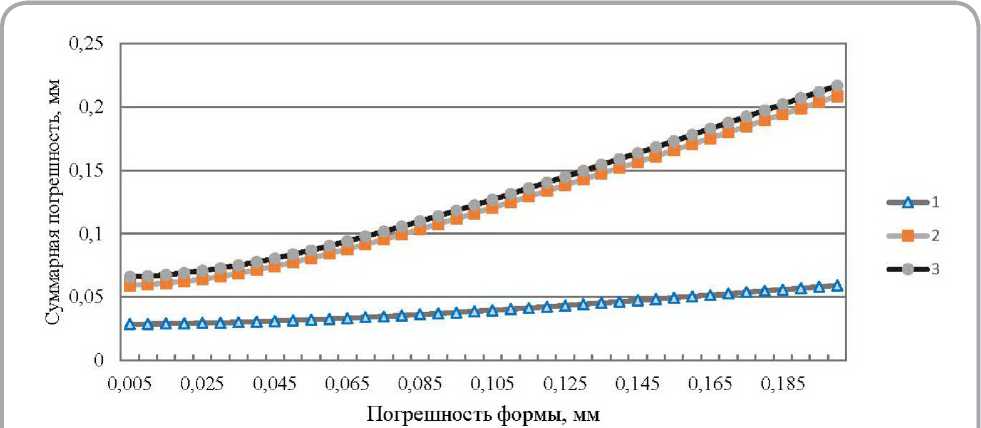
Рисунок 4 – Графики зависимостей суммарных погрешностей обработки многопериодной дорожки от погрешности формы заготовки

марную погрешность обработки многопериодной дорожки.

На рисунке 4 график 1 характеризует тангенциальную погрешность, связанную только со смещением профиля многопериодной дорожки колеса при фрезеровании; график 2 характеризует погрешность радиального смещения дорожки из-за неточной установки заготовки; график 3 показывает суммарную (радиальную и тангенциальную) погрешности обработки многопериодной дорожки при разных значениях погрешности формы базовой поверхности заготовки.

При обработке многопериодной дорожки возникают значительные погрешности от упругих деформаций станка и инструмента. Это связано со снятием неравномерного припуска при фрезеровании криволинейной поверхности. Заготовка колеса имеет предварительно обработанное центральное отверстие. Фреза при формообразовании дорожки, находясь в отверстии, углубляется в тело заготовки и снимает неравномерный припуск, перемещаясь вдоль профиля обрабатываемой поверхности. С увеличением припуска увеличиваются глубина и сила реза- ния, а, соответственно, и смещения заготовки от упругих деформаций. Стабилизировать силу резания можно оптимизацией режимов обработки. Предложено уменьшать подачу на зуб фрезы с увеличением глубины резания при обработке многопериодной дорожки. Это можно достичь программированием режимов резания на станках с ЧПУ. На рисунке 5 показаны графики погрешностей обработки с оптимизированными режимами резания.

На графиках видно, что при оптимизированных значениях глубины резания и подачи упругие деформации мало изменяются, следовательно, погрешность от упругих деформаций значительно уменьшилась. При этом суммарная погрешность обработки также уменьшилась в сравнении со значениями на диаграмме (рисунок 3).

ВЫВОДЫ

Разработан метод расчета погрешностей изготовления колес с многопериодными дорожками планетарных шариковых передач, который позволяет определить случайные и систематические технологические погрешности, рассчитать и

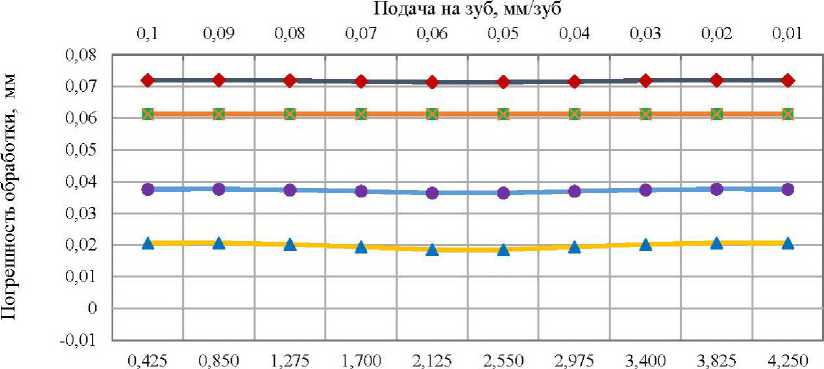
Глубина резания, мм

"♦"погрешность профиля дорожки —♦—радиальное смещение дорожки

—♦-•суммарная погрешность «♦‘«упругие деформации

Рисунок 5 – Графики погрешностей обработки с оптимизированными режимами резания

суммировать эти погрешности с использованием законов распределения случайных величин теории вероятности и разработанных компьютерных программ. На основе разработанного метода выведены формулы расчета суммарной погрешности обработки колеса, характеризующие его смещение вдоль координатных осей станка.

Разработана методика расчета, основанная на применении матричного метода, позволяющая определить погрешности обработки, возникающие в результате смещений и поворотов деталей с многопериодными дорожками. Получены матрицы преобразования пространства применительно к деталям с многопериодными дорожками, которые позволяют рассчитать координаты любой точки детали передачи. Разработанный матричный метод можно использовать для расчета погрешностей обработки, возникающих вследствие поворотов заготовки относительно системы координат станка при ее базировании, закреплении, а также из-за геометрических неточностей приспособлений и станков. В результате предложенных формул расчета получена диаграмма наибольших значений суммарной погрешности, учитывающей смещение и повороты заготовки при обработке на станке.

Получены графики, характеризующие влияние погрешности формы базовой цилиндрической поверхности колеса на суммарную погрешность обработки многопериодной дорожки. Предложена оптимизация режимов резания для фрезерования многопериодной дорожки, которая заключается в подборе оптимальных соотношений параметров глубины резания и подачи, что позволило значительно уменьшить суммарную погрешность обработки и повысить точность изготовления.

Разработанные методы можно эффективно использовать в научных исследованиях и при проектировании технологических процессов изготовления колес с многопериодными дорожками планетарных шариковых передач. При этом, применяя предложенные методики, формулы расчетов погрешностей изготовления и зависимости, представленные на графиках, можно обеспечивать требуемую точность без привлечения затратных способов изготовления, а также управлять точностью и ее повышать, изменяя технологические параметры.