Метод расчета потенциалов полезадающих элементов нелинейного ионного зеркала

Использование времяпролетных масс-спектрометров позволяет минимизировать массогабаритные и энергетические параметры аппаратуры при сохранении ее высоких функциональных характеристик, что особенно важно при проведении экспериментов по исследованию космического пространства, изучению химического состава газопылевой компоненты собственной внешней атмосферы космических аппаратов.

Применение ионных зеркал в конструкции прибора позволяет улучшить характеристики масс-спектрометра за счет увеличения пути ионов на бесполевых участках, а также реализации принципа пространственно-временнóй фокусировки ионных пакетов в плоскости детектора. Использование этих принципов обеспечивает разрешение R ~ 500 при начальном энергетическом разбросе ионов до 15 % от ускоряющего напряжения [1–3]. Однако с ростом энергетического разброса увеличивается также ошибка компенсации времени пролета, что ограничивает возможности применения данного типа анализаторов, поскольку исследование проб с высоким начальным энергетическим разбросом (например, полученных в результате высокоскоростного взаимодействия микрометеорита и мишени) требует использования высоких ускоряющих напряжений и быстродействующей аппаратуры обработки ионных спектров.

Метод расчета нелинейного ионного зеркала, предложенный в [4], позволяет обеспечить незави-

симость суммарного времени пролета ионов от их начальной энергии. Фокусировка осуществляется за счет того, что ионам с большей энергией соответствуют более длинные траектории внутри зеркала, таким образом компенсируется меньшее время пролета бесполевого участка.

Авторами был разработан метод аналитического расчета нелинейного электростатического зеркала, лишенный вышеприведенных недостатков [5]. Данный метод позволяет получить форму потенциала (1), осуществляющую точную компенсацию времени пролета для ионов с различной начальной энергией:

z = —А п

,       / ~ t0α ϕ

- L 0 arcsin

-

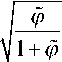
L 1

рФ + (1 + Р)

arcsin

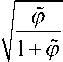
π

-2"

где t 0 — время пролета частицы с нулевой начальной энергией; α — скорость частицы после ускоряющего промежутка; р — нормированный потенциал; L 0 — суммарная длина бесполевых участков; L 1 — суммарная длина участков ускорения и торможения.

Однако физический синтез поля с заданным распределением осевого потенциала путем установки потенциалов полезадающих элементов по приведенному выше выражению невозможен. Это вызвано тем, что из-за просадок поля, вызванных

различными факторами, осевое распределение отличается от расчетного.

АЛГОРИТМ ОПТИМИЗАЦИИ ПОТЕНЦИАЛОВ ПОЛЕЗАДАЮЩИХ ЭЛЕМЕНТОВ

Для решения задачи восстановления расчетного распределения осевого потенциала авторами была разработана программа расчета потенциалов полезадающих элементов с использованием генетического алгоритма оптимизации: на каждой итерации работы алгоритма генерируется набор потенциалов для полезадающих элементов. Для каждого члена набора вычисляется поле на расчетной сетке, и осевое распределение потенциала сравнивается с целевым. Четыре члена набора с минимальным отклонением осевого распределения от расчетного участвуют в генерации набора для следующей итерации: их потенциалы "скрещиваются" и вносятся псевдослучайные "мутации" (поэтому алгоритм и получил название "генетический"). После нахождения минимума отклонения осевого распределения алгоритм переходит в режим работы с целевой функцией максимизации разрешения. Для этого в программе был реализован модуль трассировки ионов и расчета разрешения. Окончанием работы алгоритма служит установившийся режим по максимизации разрешения, т. е. от итерации к итерации увеличения разрешения не происходит.

Электростатическое поле внутри отражателя было рассчитано экстраполяционным методом Либмана, который был предложен Франкелом [6] и Янгом [7]. Данный метод является наиболее универсальным, поскольку обеспечивает достаточно быструю сходимость при сохранении устойчивости решения:

Д n + 1 _ д n ,

An, k = An, k + an         n         n         n         2        n

+ 4 ( A n + 1, k ⁺ A n , k + 1 ⁺ A n - 1, k ⁺ A n , k - 1 ⁺ h W A n , k ) ^.     (2)

Здесь a является коэффициентом релаксации,

или сходимости, определяющим скорость сходимости. Значение должно находиться в пределах 1 ^ 2. При a = 1 уравнение (2) превращается в уравнение для обычного метода Либмана, а при a >  2 процесс решения становится неустойчивым.

Значение a можно выбрать способом, предложенным Янгом [8]:

ab

» 2

^          г^

^1- п^ + ^^2 J,

где a b — оптимальное значение коэффициента сходимости; p — количество узлов сетки по вертикали; q — количество узлов сетки по горизонтали.

После расчета матрицы потенциалов требуется перейти к напряженности электрического поля. В соответствии с уравнением Максвелла, можно перейти от частных производных к приращениям (при условии их достаточной малости)

E x

E y

А V

N x

А V

^А У ’

где V — потенциал электрического поля.

Поскольку задача вычисления поля для сеток с большим количеством элементов является требовательной к вычислительным ресурсам, а метод оптимизации подразумевает большое количество итераций таких вычислений, код метода вычисления поля был портирован на язык CUDA, что позволило существенно ускорить решение задачи. Для большего ускорения возможно использование промежуточных расчетов на более грубых сетках с последующей интерполяцией результатов. Сравнительное время выполнения одной итерации вычисления для кода CPU, CUDA и CUDA c промежуточной интерполяцией приведено в таблице. Рост ускорения с ростом размерности сетки при переходе на CUDA объясняется уменьшением влияния накладных расходов при пересылке блоков данных между host-памятью и device-памятью.

Сравнительное время выполнения одной итерации вычисления (c)

Способ вычислений	Размерность сетки
	64×64	128×128	192×192	256×256
CPU×4, 3.4 ГГц	3.56	39.11	3∙60 + 1.51	10∙60 + 5.51
CUDA GF560	1.18	3.66	11.61	26.58
Interpolate	0.99	2.9	7.5	16.1

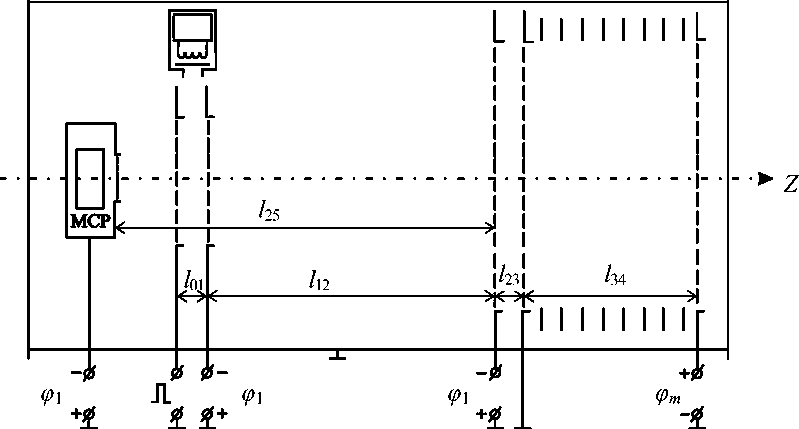
Рис. 1. Схема исследуемого масс-спектрометра

Расчет траекторий производился с использованием известных уравнений движения заряженных частиц в электрических и магнитных полях. Численный расчет траектории производился с шагом по времени, обеспечивающим, по крайней мере, 100 шагов траектории на каждую ячейку расчетной сетки. Поле в точках местонахождения ионов рассчитывалось методом бикубической интерполяции.

Воспользовавшись уравнениями (4) и переходя от дифференциала к приращению времени, получим следующие уравнения, на основе которых будет составляться алгоритм:

(         qE1

x (t + A t) = x (t) +1 vx (t) + -^- A t IA t, V        m y (t + A t) = y (t) +

V y ( t ) V

qEyi

+ ^ y - A t IA t, m J

где v x , v y — соответственно горизонтальная и вертикальная составляющие скорости частицы в текущий момент времени.

Величина пакетов выбиралась, исходя из условий гладкости полученного максвелловского распределения по энергии, и составила 100000 шт. на каждую массу. Далее для М i массы вычислялось среднее время пролета

N гср = N g Tj,              (6)

где T j — время прихода j -го иона.

Среднеквадратическое отклонение определялось согласно формуле

N ₂

G T -'jN g ( T j - T CP ) .           (7)

Разрешение по сигме:

RG. =

T . - T срI+1       ср/

2 G T

где G_T — среднеквадратическое отклонение.

РЕЗУЛЬТАТ РАБОТЫ АЛГОРИТМА

Рассмотрим работу программы на примере конструкции масс-спектрометра, приведенной на рис. 1. Здесь ϕ 1 — потенциал выталкивающего поля; ϕ m — максимальный эквивалентный потенциал, соответствующий начальному энергетическому разбросу ионов; l 12 — участок бесполевого пространства; l 01 — участок ускорения ионов; l 23 — линейный участок электронно-оптической фокусирующей системы; l 34 — нелинейный участок фокусирующей системы; l 25 — участок бесполево-го пространства при движении ионов от отражателя к приемнику (MCP).

Для расчета были выбраны следующие геометрические размеры конструкции: суммарная длина бесполевого участка L = l 12 + l 25 , равная 12.5 см, ширина тормозящего промежутка l 23 = 2.5 см, ширина ускоряющего промежутка l 01 условно равна нулю.

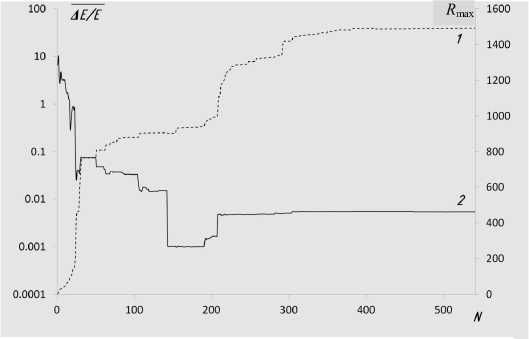
Рис. 2. Промежуточные результаты процесса оптимизации.

По левой оси ординат — средняя относительная ошибка восстановления расчетного потенциала; по правой оси ординат — разрешение прибора на 1 а.е.м.; по оси абсцисс — номер итерации; кривая 1 — зависимость разрешения от номера итерации; кривая 2 — зависимость средней относительной ошибки от номера итерации

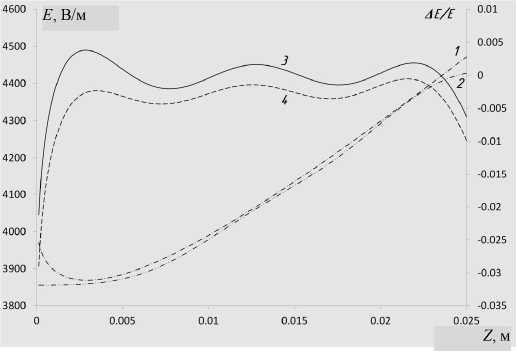
Рис. 3. Зависимость относительной ошибки от координаты внутри зеркала и целевое распределение поля внутри зеркала.

Кривая 1 — целевая зависимость поля от координаты; кривая 2 — синтезированное осевое распределение внутри отражателя; кривая 3 — зависимость относительной ошибки восстановления от координаты при оптимизации по целевой функции минимизации ошибки восстановления; кривая 4 — зависимость относительной ошибки восстановления от координаты при оптимизации по целевой функции максимизации разрешения

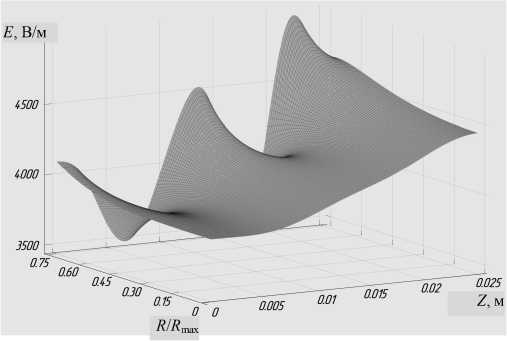
Рис. 4. Распределение поля внутри нелинейного ионного зеркала в зависимости от радиальной и продольной координат

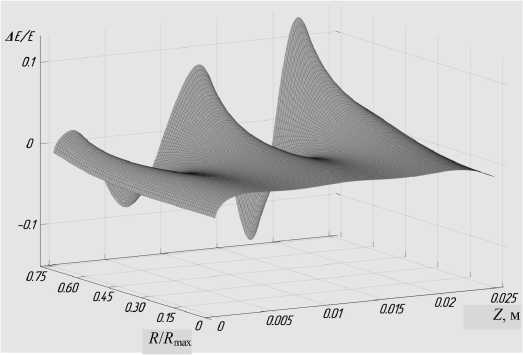
Рис. 5. Распределение относительной ошибки внутри нелинейного ионного зеркала в зависимости от радиальной и продольной координат

Результатом работы данной программы является набор потенциалов для полезадающих элементов, при использовании которых отклонение распределения осевого потенциала от расчетного является минимальным. Промежуточные результаты процесса оптимизации приведены на рис. 2.

На рис. 2 хорошо виден момент перехода программы в режим работы с целевой функцией максимизации разрешения: он приходится примерно на 190-ю итерацию. Небольшое ухудшение средней относительной ошибки восстановления рас- четного распределения потенциала при одновременном улучшении разрешения может быть объяснено тем, что при работе программы по целевой функции уменьшения средней относительной ошибки не учитывается распределение этой ошибки по координате внутри зеркала. При переходе программы в режим работы по максимизации разрешения ошибка восстановления может быть видоизменена к распределению, меньше влияющему на время пролета иона в зеркале, при этом суммарная ошибка может возрасти, но разрешение повыситься.

На рис. 3 приведено целевое и полученное в результате работы алгоритма осевые распределения электростатического поля, а также ошибки восстановления поля для конечных моментов работы алгоритма по целевой функции минимизации ошибки восстановления осевого распределения потенциала и по максимизации разрешения прибора.

Можно видеть, что наше предположение о распределении ошибки восстановления формы потенциала подтвердилось, средняя величина ошибки возросла, поскольку после оптимизации по целевой функции распределение ошибки восстановления было знакопеременным, а после оптимизации по разрешению ошибка имеет постоянный знак, при этом ее средняя величина увеличивается незначительно. Как будет показано далее, такое изменение распределения ошибки приводит к возрастанию разрешающей способности.

Используя полученные значения потенциалов полезадающих колец, было рассчитано распределение поля в зеркале и рассчитана ошибка восстановления, приведенные на рис. 4 и 5.

Из рис. 4 хорошо видно, что распределение осевой составляющей поля в объеме зеркала являются достаточно гладким и для околоосевых траекторий ионов влияние неточностей восстановления сведено к минимуму. Ошибка восстановления поля на оси прибора не превышает 3 % вблизи сеток, ограничивающих зеркало, и 0.5 % в остальной части отражателя. На периферии рефлектора относительная ошибка восстановления не превышает 10 %.

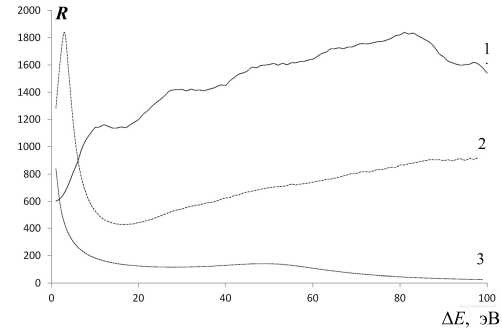
Рис. 6. Разрешение в зависимости от энергии ионов.

1 — нелинейное зеркало с оптимизацией по разрешению; 2 — нелинейное зеркало с оптимизацией по минимальной ошибке; 3 — линейное зеркало

Рис. 7. Разрешение в зависи- 3 мости от массы.

• 1    — нелинейное зеркало, 100 % разброс; 2 — нелиней-

• 4    ное зеркало, 50 % разброс;

• 3    — линейное зеркало, 50 % разброс; 4 — линейное зеркало, 100 % разброс

М , а.е.м.

Зависимости разрешения от энергетического разброса для линейного зеркала и нелинейного зеркала с оптимизацией по целевой функции минимизации ошибки и по разрешению приведены на рис. 6. Как видно из приведенных графиков, для результирующего распределения с минимальной ошибкой восстановления максимальное разрешение достигается при энергетическом разбросе ионов, не превышающем 10 % от ускоряющего напряжения, затем разрешение резко снижается. Для распределения, оптимизированного по разрешению, фокусировка ионов по энергиям превосходит результаты первого способа оптимизации более чем в 2 раза на всем диапазоне энергий, за исключением диапазона малых разбросов, где результаты первого способа превосходят результаты второго.

Зависимости разрешения от массы для 50 и 100 % начального энергетического разброса для традиционного рефлектрона и масс-спектрометра с нелинейным зеркалом приведены на рис. 7. Можно видеть, что для нелинейного зеркала зависимость разрешения от энергетического разброса минимальна и превосходит 10 единиц даже для масс порядка 100 а.е.м.

ЗАКЛЮЧЕНИЕ

Как видно из приведенных графиков, предложенный метод превосходит классический линейный рефлектрон в 10–50 раз в зависимости от начального энергетического разброса ионов. Данный метод аналитического расчета нелинейного распределения потенциала электростатического ионного зеркала в совокупности с применением алгоритма генетической оптимизации потенциалов полезадающих элементов позволяет существенно расширить диапазон разрешаемых масс, а также расширить диапазон допустимых начальных энергий ионов вплоть до 100 %.