Метод расчета поверхности коленного сустава

Основная роль нижних конечностей у человека — опора и перемещение тела в пространстве, что обеспечивается функциональным единством всех ее элементов. Ноги могут выполнять три функции: придавать туловищу устойчивое положение, то есть работать статически, удлинять и укорачивать продольную ось тела и вращать его в разных направлениях и, наконец, действовать самостоятельно. Однако все это возможно только при здоровых, нормально развитых нижних конечностях. Форма нижних конечностей в процессе роста и развития организма меняется. Ребенок рождается с незначительной деформацией ног в виде genu varum , которая постепенно к 2—4 годам переходит в физиологическое вальгусное искривление колена. Вальгусная установка в коленном суставе достаточно выражена уже к концу первого года жизни ребенка и возрастает до 10-летнего возраста. Величина физиологического искривления коленного сустава внутрь у детей до 10 лет варьирует от 3 до 8°, а у взрослых — от 7 до 8°. По данным И. П. Шуляка и Л. А. Янковича (1967), углы физиологического вальгуса колеблются от 0 до 14°.

В зависимости от степени и вида фронтального искривления коленного сустава возникают статические перегрузки наружных или внутренних мыщелков бедра и голени. При этом необходимо выделить два вида сил, действующих на коленный сустав — силы сжатия и растяжения. Силы сжатия обнаруживаются на вогнутой стороне и влияют в основном на костную и хрящевую ткани. Силы растяжения возникают на выпуклой стороне; они преимущественно воздействуют на мягкие ткани — капсулу, связки, сухожилия. Возникающие статические перегрузки приводят к определенным структурным сдвигам в костной и хрящевой тканях.

Замечательное свойство костной ткани перестраивать свою структуру в зависимости от воздействия механических и динамических факторов, а также от изменения функции доказана многими отечественными и зарубежными исследователями. При вальгусном искривлении коленного сустава, когда наружные половины костей бедра и голени испытывают большее давление, чем внутренние, компенсаторные перестройки костей выражаются в утолщении коркового слоя диафизов бедра и голени с наружной стороны. Кроме того, увеличиваются размеры наружной половины бедренной и большеберцовой костей в области метафизов, а также наружных мыщелков бедра и голени с громадным скоплением «утолщенных костных балок».

Другим видом перестройки костной ткани компенсаторного характера при данной деформации является утолщение малоберцовой кости. Варус-ные искривления колена сопровождаются аналогичными структурными изменениями внутренних половин бедренной и большеберцовой костей.

Неравномерные силовые нагрузки на коленный сустав при genu valgum et genu varum приводят к преждевременной изнашиваемости суставных хрящей в местах наибольшего приложения силы с последующим развитием деформирующего артроза.

Показателем распределения статических нагрузок на коленный сустав является механическая ось нижней конечности, которая в норме проецируется на центр коленного сустава. При genu valgum et genu varum механическая ось смещается соответственно в сторону наружных или внутренних мыщелков бедра и голени пропорционально величине искривления. Поэтому мыщелки испытывают статическую перегрузку, что является причиной перестроек костной ткани и образования деформирующего артроза.

В практическом отношении для нормализации нагрузок на коленный сустав во время оперативной коррекции фронтальных искривлений колена важно восстановить анатомическую ось бедра и голени как основное условие проекции механической оси нижней конечности на центр коленного сустава.

При практическом применении данного положения появляется ряд вопросов:

• 1.    Как найти распределение статических нагрузок на коленный сустав?

• 2.    Как найти проекцию механической оси на поверхность коленного сустава?

• 3.    Как провести оперативную коррекцию, чтобы восстановить нормальное распределение нагрузки по поверхности коленного сустава?

• 4.    Какое распределение нагрузки по поверхности коленного сустава считать нормальным?

Для ответа на поставленные вопросы рассмотренных методик не хватает, так как рентгенологические исследования компьютерной томограммы, магнито-резонансной томограммы не позволяют судить о реальном нагружении тканей костей и связок, так как направлены на визуализацию данных тканей, а не на измерение их физических свойств. Методы стабилометрии используют при исследовании баланса вертикальной стойки и ряда переходных процессов посредством регистрации положения, отклонений и других характеристик проекции общего центра тяжести на плоскость опоры, и они не позволяют находить распределение нагрузок по заданным точкам человеческого тела. Также не хватает набора рассмотренных биомеханических характеристик, которые направлены на определение характера функционирования человеческого тела в целом, а не нахождение параметров функционирования отделов человеческого тела и их механического взаимодействия.

Цель: разработать метод расчета поверхности коленного сустава для определения биомеханических характеристик сустава в норме и при его патологии.

Предложенный способ основывается на методе конечных элементов. Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, такую как температура, давление и перемещение, можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области. В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. Итак, при построении дискретной модели непрерывной величины поступают следующим образом:

• 1.    В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

• 2.    Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

• 3.    Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

• 4.    Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента [ 2, 3, 4].

Использование рентгеновского компьютерного (рис. 1) и магнитно-резонансного (рис. 2) томографических исследований дает четкую визуализацию костных и мягкотканых структур коленного сустава, что помогает получить морфометрические данные об индивидуальных особенностях его строения. Возможно получение 3D-модели сустава с помощью программного обеспечения, имеющегося в консоли томографа [1].

При помощи программного обеспечения eFilmLt, полученную 3D-модель коленного сустава можно рассечь на нужное количество продольных и поперечных срезов. Воспользовавшись полученными срезами в продольном сечении в плоскостях (x, z) и (y, z), можно, сопоставив их, получить область для дискретизации и найти координаты интересующих нас узлов. Для этого необходимо на рис. 3 в плоскости (x, z) выбрать точку x, тогда на этом же рисунке мы можем определить z- компоненту. Для определения y-компоненты не- обходимо взять соответствующий рис. 3 рисунок в плоскости (у z). После чего мы меняем x на рис. 2

и также находим для этого значения z-компоненту, но у-составляющая не меняется для рис. 3, то есть остается постоянной. Вследствие этой процедуры мы найдем все узлы для одного среза. Далее, взяв следующие срезы, получаем следующее значение у-компоненты, которое будет постоянным для переменных x и z. Таким образом, повторяя эту операцию для всех срезов, мы полу- чим искомые координаты всех узлов.

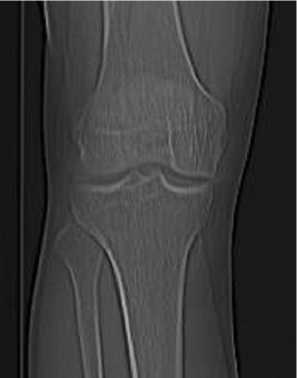
Рис. 1. Рентгеновская компьютерная томография

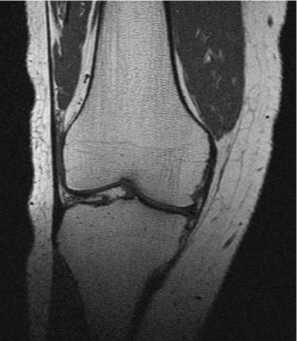
Рис. 2. Магнито-резонансная томография

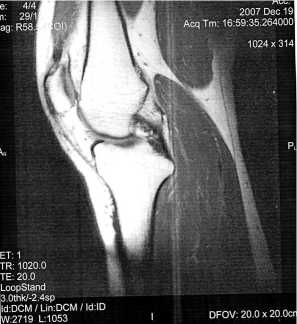
Рис. 4 Снимок в поперечном сечении ( у z)

Как видно из рисунков, мы при помощи вышеизложенной процедуры разбили нашу область на четырехугольные элементы, но нам известно, что любой четырехугольник всегда можно разбить на треугольные элементы (рис. 5).

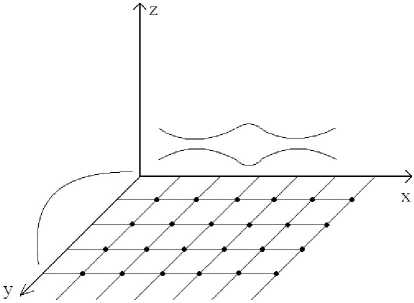
Рис. 5. Разбиение области на элементы

Таким образом у нас есть все необходимое для того, чтобы посчитать площадь поверхности коленного сустава с помощью метода конечных элементов. Но для этого нам необходимо знать, как считается площадь треугольника по трем координатам всех вершин.

Для вывода интересующей нас формулы рассмотрим на рис. 6 отрезок AB в плоскости (z, x) и спроецируем его на плоскость (у x) .

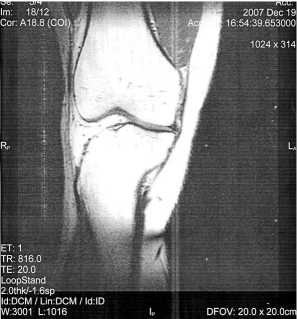
Рис. 3. Снимок в продольном сечении ( x, z )

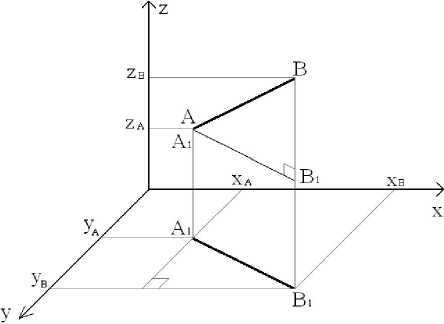
Рис. 6. Проекция АВ в (z, x) на (у, x)

Из рис. 6 видно, что если применить теорему Пифагора, то можно найти длину спроецированного отрезка А1В1:

S = V p ( p - AB )( p - BC )( p - CA ),        (1.2)

Г, 2                2

A1B1 = /^xB ^{- X}A ) ^{+( y}B ^- yA )

(0.1)

где p =

AB + BC + CA 2

полупериметр треугольника.

Таким образом, найдя площади всех треуголь-

Далее, полагая, что отрезок А1В1 равен отрезку AB, то есть А1В1 = АВ, то применяя теорему Пифагора, мы можем найти длину отрезка AB:

ных элементов, на которые мы разбили область

2      2)          2         2        2)

^AB = / zB - zA ) ⁺( A 1 ^B1 ) ^{= t}J( ^XB ^{- X}A ) ⁺( ^yB ^{- y}A ) ⁺( ^zB ^{- z}A ) (^0.2)

коленного сустава и просуммировав их, мы получим искомую площадь нижней поверхности коленного сустава. Полученные результаты являются фундаментом для дальнейшей разработки аппаратно-программного комплекса для диагностики и прогнозирования течения дегенеративных заболеваний коленного сустава.

Аналогично вышеизложенным выкладкам можно получить длины сторон треугольного элемента:

^AB = V ^{( X}B - ^X _A ^{)2 + (} y_B - y_A)2 ^{+ ( z}B - ^zA)2 BC = ( ^xC - ^xB )^{2 +} ( yC - y_B S2 ⁺ ( ^zC - ^zB )² CA =^^{( x} _A - ^xC S² + ⁽ y_A - yC S² + ⁽ z_A - zC S²

(1.1)

После чего мы можем найти площадь треугольника, воспользовавшись формулой Герона: