Метод расчета радиальной электромагнитной опоры турбомолекулярного вакуумного насоса

Первоначально активные магнитные подшипники (АМП) были разработаны с целью преодоления недостатков обычных подшипников качения или скольжения. В исследовательских лабораториях они показали свою способность работать в вакууме без какой-либо смазки и с отсутствием загрязнений рабочего пространства, на высоких скоростях и с возможностью изменения жесткости и демпфирования в широких пределах. Первые примеры практического использования активных магнитных подвесов относятся к 40-м годам XX столетия. Они описаны в работах Д. Бимса [4] по созданию ультрацентрифуг и роторных вакуумметров, Д. Хризенгера [1] по подвеске моделей в аэродинамических трубах и О. Г. Кацнельсона и А. С. Эдельштейна [6] по созданию весоизмерительных приборов. Подробное описание конструктивных и схемных решений, использованных в перечисленных работах, приведено в [7]. Сегодня магнитные подшипники введены в промышленный мир как очень ценный элемент машины с рядом особенностей и широким диапазоном применений.

Расчет проводился по следующему алгоритму.

• •    Задается быстрота действия ТМН, род и температура откачиваемого газа.

• •    Рассчитываются геометрические параметры колеса ТМН. Определяется диаметр вала ТМН.

• •    Рассчитываются геометрические и силовые характеристики электромагнитной опоры.

Внешний диаметр колеса D2 определяется по методу, предложенному в [5]

D2 =

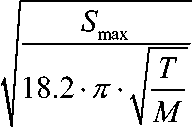
________ a I b + h IH ________ ( a I b + h IH ) • I_x - X-h IH • I₂

где 5 _max - максимальная быстрота откачки ТМН, T - температура откачиваемого газа, M - молярная масса откачиваемого газа, a/b -отношение ширины межлопаточного канала колеса ТМН к его длине, h/H -отношение толщины лопатки колеса ТМН к толщине колеса ТМН, X -отношение внутреннего диаметра лопаток колеса к внешнему, I , I -коэффициенты, зависящие от окружной скорости колеса, наиболее вероятной скорости движения молекул и отношения внутреннего диаметра лопаток колеса к внешнему.

Следовательно, диаметр вала ТМН

d = 4 • D                       (2)

где 4 - отношение диаметра колеса под вал к внешнему диаметру колеса.

Магнитная сила, действующая на элемент площади ферромагнитного тела dA в однородном магнитном поле с индукцией в зазоре B [8],

2 dF =---dA, 2Щ где ^ = 4п • 10-7 Гн/м - магнитная постоянная.

Отсюда следует, что электромагнит с плоским зазором создает тяговое усилие F = 0,4 • 10 6 B ² A , или 40 Н/см² при B = 1 T.

Тяговое усилие электромагнита, создаваемое, например, полюсами 1 и 2 (рис. 1), определяется интегральной суммой проекций элементарных сил на ось Ox

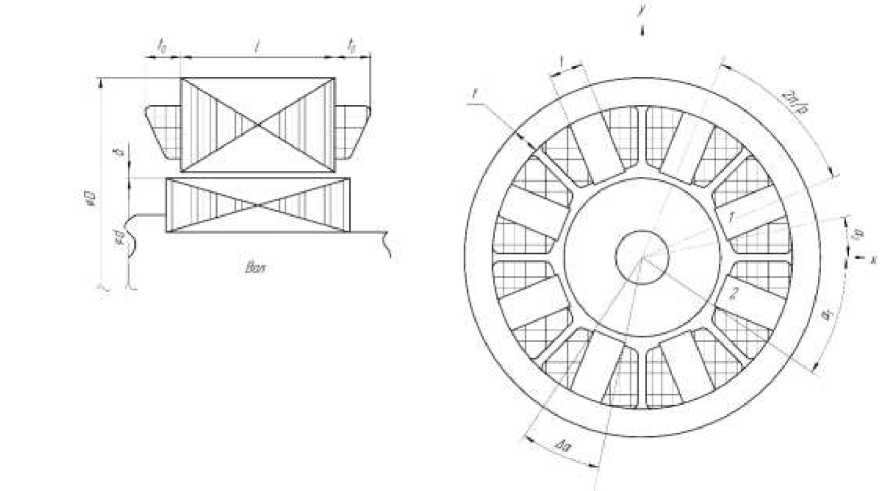
Рис. 1. Схема радиального подшипника. а - угол, отсчитываемый от оси Ox

B 2 ld F =-- 2 ^ 0 2

' а +А а             а +А а           ' J cos a d a + J cos a d a V   а 1                       а 2                 7

Учитывая, что а = -22,5°-Аа /2, а2 = 22,5°-Аа /2, нетрудно установить ,что сумма интегралов в уравнении (4) приводится к виду 4 cos 22,5° sin(Aa /2) = 3,695 sin(Aa / 2).     Аналогичным    образом вычисляется тяговое усилие для АМП с числом полюсов p = 16,24,...,32. Обобщающая формула для тягового усилия радиального АМП принимает вид

„ B ² paid . Аа

F =          sin ,

2 ^ о   4      2

где a - коэффициент, зависящий от числа полюсов, a = 0,924 при p = 8, a = 0,906 при p = 16, a = 0,903 при p = 24 .

Поскольку полюсный угол Аа = t / (d /2) мал, можно положить sin(Aa /2) = t / d и привести выражение (3) к виду paltB2 F =------.

⁸ ^ 0

Чтобы найти удельное тяговое усилие на единицу площади диаметрального сечения цапфы f = F / id , нужно задаться шириной n d полюса t . Пусть полюс занимает половину полюсного деления, т.е. t = ---.

2 p

Тогда имеем f = F /(id) = 15,6aB2 Н/см2

В частном случае восьмиполюсного подшипника f = 14,4 B ² Н/см².

АМП, как и любой другой тип подшипника, должен обладать заданной несущей способностью F . Применительно к АМП под несущей способностью понимается максимальное тяговое усилие, которое может развиваться в течение длительного времени без перегрева обмотки. В ряде случаев статическая нагрузка на подшипник Q известна точно, в других случаях - приближенно. Однако всегда значение должно быть больше Q настолько, чтобы оставался запас для отработки динамических нагрузок. Также должна быть учтена возможность непредвиденных нагрузок. Обычно коэффициент запаса принимают равным Fmaх / Q = 2. Определяющим параметром при расчете геометрических характеристик подшипника является индукция в зазоре B. Она, в свою очередь, зависит от магнитных свойств используемой стали. В отличие от электрических машин, магнитное насыщение в АМП не допускается, поскольку оно вызывает потерю управляемости. Поэтому максимальное значение магнитной индукции в стали не должно превышать 1,4 Т для электротехнической стали и 1,8 Т - для кобальтовой стали [3]. Индукция в зазоре при этом будет на 10-15% меньше, чем в стали, из-за наличия потоков рассеяния и составлять 1,2 Т при использовании электротехнической стали и 1,6 Т - кобальтовой стали. Очевидно, что при индукции в зазоре B = Bmaх, подшипник должен развивать тяговое усилие, равное требуемой несущей способности F . Плотность тока в проводниках катушек при этом должна быть равна допустимому значению jmax .

Рассмотрим восьмиполюсный АМП и сформулируем задачу расчета его геометрии следующим образом. Пусть задан диаметр цапфы d и длина пакета l. Пусть также заданы зазор 3 и допустимая плотность тока j_mах . Требуется найти внешний диаметр D и ширину полюса t, при которых тяговое усилие было бы максимальным, а индукция в зазоре при этом была ^бы равна B _тах .

Индукцию в зазоре найдем из закона Ампера для магнитной цепи, по которому МДС, создаваемая катушками обоих полюсов, равна сумме падений магнитных напряжений в двух воздушных зазорах и в стали.

Магнитная цепь не насыщена, поэтому для простоты магнитным сопротивлением стали пренебрегаем. Тогда имеем jmax kcuA = — 28, ^0

где k - коэффициент заполнения площади паза А медью (ориентировочно kCu = 0,3^0,5) [2].

Площадь, занимаемая обмоткой в пазу

A =

Г D - d

V 2   2

— t

V nd

К 2

^

— t

Отсюда выражение для индукции в зазоре

B ( D , t ) = C_B

r D — d

V 2   2

^

— t

r nd

V 2

^

— t

и выражение для тягового усилия

F ( D , t ) = C f C —

r D

V 2

d

л2

— t

r nd

V 2

^— t t ,

где C и C - константы, определяемые соотношениями:

= M o ^k Cu ^j max . C = PaL

28   ’ ^F    8m '

Задача расчета геометрии подшипника математически сводится к задаче на условный экстремум: требуется найти максимум функции F(d, t) при дополнительном условии B (d, t) = Bmax, которое можно записать в виде уравнения

^ ( D , t )

(D - d

( 2   2

-

V nd t V 7k 2

^

- t

-

^B max

CB

= 0.

Метод решения такой задачи хорошо известен. Формируем функцию

Ф (d , t ) = F (d , t ) + Хф^ ^ d, t ), где B = B _max    - множитель Лагранжа.

Неизвестные D и t находятся из совместного решения уравнения (11) и двух уравнений:

d Ф (D, t) =0 dD дФ ( D, t) --------= 0.

d t

Решение задачи дается соотношениями t = 0.392d - 0.885

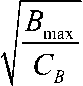
D = 2 d - 0.546 1

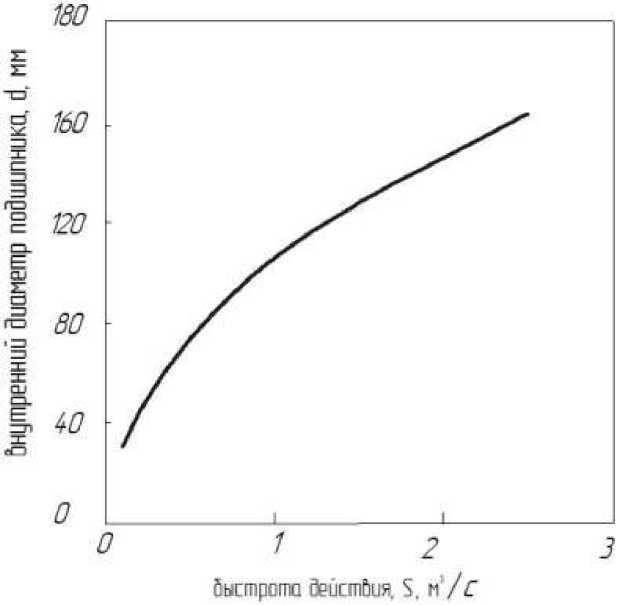
Рис.2. Зависимость внутреннего диаметра подшипника от быстроты действия насоса.

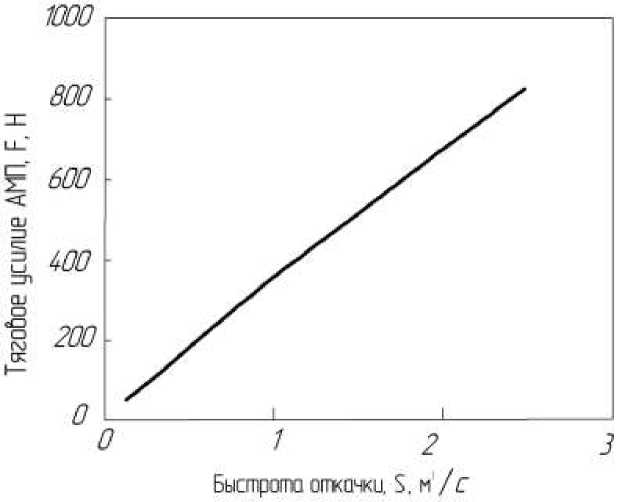
Рис.3. Зависимость максимального тягового усилия АМП от быстроты действия насоса

Видно, что в оптимальном подшипнике внутренний диаметр d должен быть немного больше половины наружного диаметра D . Ширина полюса t в зависимости от соотношения между выбранными значениями параметров B_{ma х}, j_max и 5 может меняться в определенных пределах. Обычно эти параметры выбирают так, чтобы полюс занимал примерно половину полюсного деления, равного nd/8.

Требуемое значение несущей способности F_max может быть достигнуто соответствующим выбором длины пакеты стали l . Продольный размер статора I_с = I + 2t₀, где t₀ = (7^- — t)/2 - длина лобовой части обмотки.