Метод расчета резонансных частот ТЕМ-камеры

При проведении испытаний электронных компонентов и систем используются ТЕМ-камеры [1]. При больших размерах поперечного сечения регулярной части ТЕМ-камеры на некоторых частотах в ней могут возбуждаться паразитные резонансы электромагнитного поля. Как показано в [2, 3], причиной возбуждения резонансов являются высшие типы волн, распространяющиеся в регулярной части ТЕМ-камеры. При возбуждении резонансов в ТЕМ-камере в регулярной части в месте расположения объекта испытаний электромагнитное поле становится неравномерным, что препятствует проведению испытаний на электромагнитную совместимость.

Целью работы является определение собственных типов волн, обусловливающих резонансы в ТЕМ-камере и расчет ее резонансных частот.

1.    Существующие методы расчета частотных характеристик объемных резонаторов

При расчете частотных характеристик ТЕМ-ка-меру можно интерпретировать как многомодовый объемный резонатор.

В настоящее время известны работы, в которых рассматриваются внешние электрические характеристики многомодовых объемных резонаторов с использованием высших распространяющихся типов волн. Такие резонаторы представляют собой, как правило, отрезок круглого или прямоугольного волновода большого сечения, в котором выполняются условия распространения для одного или нескольких высших типов волн. На входе и выходе такого регулярного отрезка включены конусные или пирамидальные переходы, для которых во всем диапазоне частот в области малых размеров поперечного сечения распространяющимся является только основной тип волны.

Такие резонаторы на высших типах колебаний получили название резонаторов на сверхразмерных волноводах или резонаторов на запертых модах [4]. Резонансы в этих структурах могут быть обусловлены только распространяющимися в регулярной части основным или высшими типами волн.

В регулярной части ТЕМ-камеры также выполняются условия распространения для нескольких высших типов волн. В то же время во всех сечениях пирамидальных переходов условия распространения выполняются только для одного основного типа волны. В результате этого какой-либо высший тип волны, распространяющийся в регулярной части ТЕМ-камеры, доходит до критического сечения в пирамидальном переходе и отражается от него.

Представляет большой теоретический и практический интерес определение условий возбуждения резонансов в ТЕМ-камере, выявление причин их возникновения и расчет внешних электрических характеристик всей ТЕМ-камеры.

В настоящее время известны работы по расчету характеристик резонаторов на запертых модах [4-6]. Однако в этих работах заранее известен высший тип волны, который обусловливает резонанс, и задача заключается в определении внешних электрических характеристик резонатора.

Для ТЕМ-камеры необходимо решить другие задачи:

• •    идентифицировать тип волны, обусловливающий появление резонансов;

• •    определить структуру или элемент резонатора, обеспечивающего связь резонансного поля с полем основной волны;

• •    рассчитать амплитудо-частотную характеристику резонатора на запертых модах;

• •    определить резонансные частоты.

2.    Идентификация типов волн, обусловливающих резонансы в ТЕМ-камере

Все перечисленные выше задачи можно решить, если воспользоваться предложенным авторами методом расчета электродинамических характеристик объемных резонаторов с использованием многомодовых матриц рассеяния.

При расчете частотных характеристик ТЕМ-камеру можно представить в виде каскадного соединения многомодовых многополюсников, описывающих электродинамические характеристики пирамидальных переходов и ее регулярной части (рис. 1).

В [3] рассчитана частотная характеристика ТЕМ-камеры, по которой определены ее резонансные частоты в диапазоне частот от 0 до 30 МГц при учете в ее регулярной части семи распространяющихся типов волн. В качестве объекта для расчета частотных характеристик была выбрана ТЕМ-камера, установленная в Дирекции по техническому развитию ОАО «АВТОВАЗ» и предназначенная для проведения ис- пытаний транспортных средств на электромагнитную совместимость.

Представляет большой интерес выяснить причины появления резонансов и условия их возникновения. Для этого необходимо определить типы волн, обусловливающие появление резонансов.

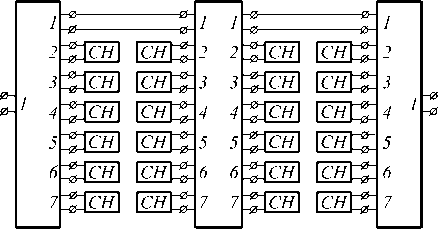
Рис. 1. Расчетная модель ТЕМ-камеры при учете только одного основного типа волны в регулярной части (СН – согласованная нагрузка)

Известно, что элементы многомодовых матриц рассеяния регулярной части ТЕМ-камеры и пирамидальных переходов не зависят от параметров нагрузок, подключенных к их входам. Это позволяет при анализе частотных характеристик всей ТЕМ-камеры ограничить число учитываемых в регулярной части высших распространяющихся типов волн и тем самым выявить те типы волн, которые обусловливают появление резонансов. Для этого ко входам многополюсников, соответствующих тем типам волн, которые необходимо исключить из анализа, следует подключить согласованные нагрузки. В результате этого в алгоритме расчета внешних электрических характеристик будут учитываться только анализируемые типы волн.

Рассчитаем частотную характеристику ТЕМ-камеры в случае, когда в регулярной части учитывается только один первый распространяющийся тип волны. Для этого ко входам многополюсников с номерами 2-7, в которых распространяются эти собственные типы волн, необходимо подключить согласованные нагрузки. В этом случае расчетная модель ТЕМ-камеры будет иметь вид, показанный на рис. 1.

Используя результаты расчета многомодовых матриц рассеяния пирамидальных переходов [7] и алгоритм расчета каскадного соединения многополюсников [8], можно рассчитать частотную характеристику ТЕМ-камеры при учете только одного первого собственного типа волны. Результаты расчета частотной характеристики приведены на рис. 2.

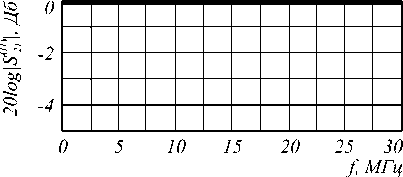
Рис. 2. Частотные характеристики ТЕМ-камеры при учете первого собственного типа волны в ее регулярной части

Из представленной частотной зависимости коэффициента передачи ТЕМ-камеры следует, что при учете только первого собственного типа волны в ее регулярной части резонансы отсутствуют. Обусловлено это тем, что нерегулярные отрезки линий передачи (пирамидальные переходы) имеют малые коэффициенты отражения для основной волны, и в них не выполняются условия, необходимые для возбуждения резонансов.

Рассмотрим расчет частотной характеристики ТЕМ-камеры при учете в ее регулярной части 1, 2, 3, 4, 6 и 7 распространяющихся типов волн.

Расчетная модель ТЕМ-камеры для этого случая показана на рис. 3.

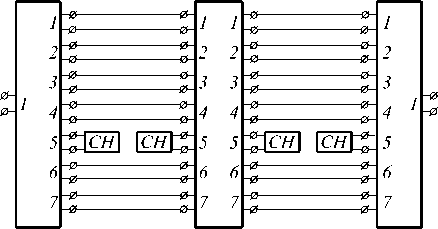
Рис.3. Расчетная модель ТЕМ-камеры при учете в регулярной части 1, 2, 3, 4, 6 и 7 распространяющихся типов волн

Рассчитанная частотная характеристика ТЕМ-камеры совпадает с частотной характеристикой при учете только основной Т-волны, изображенной на рис. 2. Это означает, что эти распространяющиеся типы волн не вызывают появление резонансов в ТЕМ-камере.

Особенностью этих типов волн является отсутствие их возбуждения основной волной в пирамидальных переходах, так как для этих типов волн соответствующие элементы матриц рассеяния обоих пирамидальных переходов равны нулю во всем диапазоне частот [7].

Рассмотрим расчет частотной характеристики ТЕМ-камеры при учете в регулярной части первого и пятого собственных типов волн. Расчетная модель ТЕМ-камеры для этого случая показана на рис. 4.

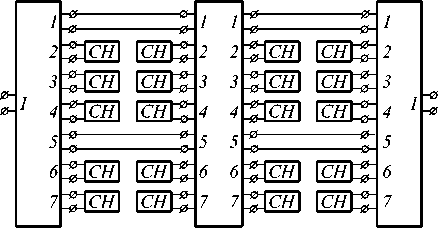
Рис.4. Расчетная модель ТЕМ-камеры при учете в регулярной части первого и пятого распространяющихся типов волн

Проведенные расчеты частотной характеристики данной модели показали, что частотная зависимость выраженного в децибелах модуля коэффициента передачи ТЕМ-камеры по основной моде при учете в

ее регулярной части первого и пятого распространяющихся собственных типов волн, приведенная на

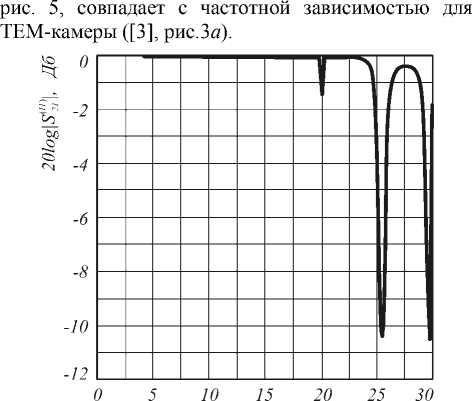
/МГц

Рис. 5. Частотная характеристика ТЕМ-камеры по основной моде при учете в ее регулярной части первого и пятого собственных типов волн

Это означает, что именно пятый собственный тип волны регулярной части ТЕМ-камеры обусловливает появление резонансов в ТЕМ-камере.

Причиной возбуждения этого типа волны в регулярной части ТЕМ-камеры является наличие в ее конструкции пирамидальных переходов, в которых при распространении основного типа волны происходит возбуждение пятого высшего типа волны [7].

Используя алгоритм расчета каскадного соединения многополюсников [8], можно записать выражение для коэффициента передачи ТЕМ-камеры по основной моде при учете основной волны и 5-го высшего типа волны

[ s 21 ] =[ ² s 21°   ² s 21⁵⁾ ]•

Г

• [ E ]

^^^^^B

1 (11) ^S 21

1 (51)

^S 21

¹ S™ e

¹ S (⁵¹) e - i ⁽⁹ i ⁺⁹ 5 )

¹ S ⁽¹⁵^ e - i ^{(9 | +9} 5 )     2 s (ii)

¹ S 25⁵⁾ e -^{i 2 9} 5

S

- 1 20(15)

^S 22

2 0(55)

^S 22   J ,

• ,(4)

4. Условия возбуждения резонансов в ТЕМ-камере

Представляет интерес определить условия возбуждения резонансов для этого типа волны в ТЕМ-камере. Для этого запишем выражения для многомодовых матриц рассеяния пирамидальных переходов _ ¹ S ] , _ ² S ] и регулярной части ТЕМ-камеры [ S ] при учете первого и пятого типов волн.

	[ 1 S 111	1 (11) S 12	1 (15) S 12
[ 1 s ]=	1 (11) S 21	1 (11) S 22	1 (15) S 22	,                        (1)
	1 (51) _ S 21	1 (51) S 22	1 (55) S 22
	2 (11) S 11	2 S (15)	2 (11) S 12	1
[ 2 S ] =	2 S 251)	2 S (55)	2 (51) S 12	,                       (2)
	2 0(11) _ S 12	2 (51) S 12	2 (11) S 22

	■ 0	0	exp( - i 9 1 )	0 ■
[ s ] =	0	0	0	exP( - i 0 5 )	, (3)
	exp( - i 9 1 )	0	0	0
	_ 0	eXP( - i 0 5 )	0	0 ]

где ⁹ 1,5 = У 1.5 L .

где [ E ] - единичная матрица.

Резонанс соответствует минимуму коэффициента передачи на основной моде ТЕМ-камеры. Для произвольных значений элементов матриц рассеяния пирамидальных переходов из соотношения (4) получить условие резонанса в простой аналитической форме не представляется возможным, однако в приближении слабой связи основного типа волны с 5-м высшим типом такое аналитическое выражение условия резонанса имеет вид

1 ф 2⁵2⁵⁾ + 2 9 5 + ² ф (1⁵⁾ = 2 п к , (5)

где к = 0, ± 1, ± 2,..., 9 5 - фазовый набег 5-го типа волны в регулярной части ТЕМ-камеры, ¹ ф 22⁵⁾ , ² ф ⁽5⁵⁾ - фазовые углы коэффициента отражения 5-го типа волны соответственно от 1-го и 2-го пирамидальных переходов.

Физически это условие означает для 5-го высшего типа волны синфазность полей, переотраженных от пирамидальных переходов, в какой-либо точке внутри регулярной части ТЕМ-камеры.

Резонансные частоты ТЕМ-камеры можно определить из соотношения (5) численно. Входящие в это соотношение фазовые углы 9 5 , 1 ф 25₂⁵⁾ и ² ф (5⁵⁾ зависят от частоты.

На рис.6 приведены рассчитанные частотные зависимости фазового сдвига5-го собственного типа волны 9 5 = y ₅ L , вносимого регулярной частью ТЕМ-камеры длиной L (кривая 1).

Из представленной зависимости видно, что до частоты 17,5 МГц фазовый угол не изменяется и численно равен 0°. Обусловлено это тем, что в указанном частотном диапазоне пятый собственный тип волны является для регулярной части ТЕМ-камеры нераспространяющимся. При увеличении частоты свыше 17,5 МГц 5-й собственный тип волны становится распространяющимся, и фазовый сдвиг коэффициента передачи изменяется.

Рассчитанная частотная зависимость фазы коэффициента отражения 5-го собственного типа волны [7] для первого перехода 1 Ф 22⁵) приведена на рис. 6 (кривая 2).

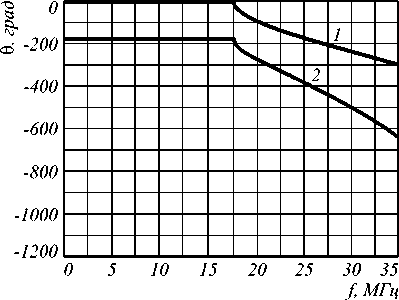
Рис. 6. Частотные зависимости фазового сдвига 5-го собственного типа волны θ ₅ , вносимого регулярной частью ТЕМ-камеры (кривая 1), и фазы коэффициента отражения от пирамидального перехода 5-го собственного типа волны ¹ ϕ ⁽ ₂ ⁵ ₂ ⁵⁾ (кривая 2)

Из представленной зависимости следует, что при частотах менее 17,5 МГц фаза коэффициента постоянна и равна -180°. Обусловлено это тем, что в указанном частотном диапазоне в пирамидальном переходе не выполняются условия распространения пятого собственного типа волны, а критическое сечение для этого типа волны расположено в сечении пирамидального перехода с наибольшими размерами.

По мере увеличения частоты свыше 17,5 МГц плоскость критического сечения, от которого отражается пятый собственный тип волны, смещается внутрь пирамидального перехода, и фаза коэффициента отражения ¹ ϕ ⁽ ₂ ⁵ ₂ ⁵⁾ изменяется.

Аналогичный вид имеет частотная зависимость фазы коэффициента отражения второго пирамидального перехода ² ϕ ₁ ⁽⁵ ₁ ⁵⁾ .

Спектр резонансных частот ТЕМ-камеры можно определить по соотношению (5). На рис. 7 представлена рассчитанная частотная зависимость суммарного фазового сдвига ¹ ϕ ⁽ ₂ ⁵ ₂ ⁵⁾ + 2 θ ₅ + ² ϕ ₁ ⁽⁵ ₁ ⁵⁾ для ТЕМ-камеры.

Из представленного графика видно, что условия резонанса, описываемые соотношением (5), выполняются для частот 20 МГц, 25,8 МГц и 29,6 МГц, что соответствует ранее проведенным расчетам и результатам экспериментальных исследований.

Таким образом, предложенный метод расчета частотных характеристик ТЕМ-камеры с использованием многомодовых матриц рассеяния адекватно описывает в ней резонансные явления.

Заключение

Предложенная методика идентификации собственных типов волн позволила выявить, что возбуждение резонансов в ТЕМ-камере обусловлено пятым собственным типом волны в ее регулярной части.

Определено, что причиной возбуждения этого типа волны является наличие в ТЕМ-камере пирамидальных переходов.