Метод расчета среднеинтегральной температуры влажного материала в процессе конвективной сушки

Процесс сушки отличается большой сложностью и представляет целый комплекс взаимосвязанных и взаимопроникающих явлений тепловлагообмена, протекающих как в материале, так и в объеме пограничного слоя вблизи поверхности материала. Поэтому до настоящего времени крайне ограничена возможность использовать результаты теоретических решений тепломассобмена для реальных условий сушки влажных тел. В таких случаях, как показала практика сушки, используются полуэмпирические или чисто эмпирические методы расчета, на основе которых возникли традиционные способы расчета кинетики тепловлагообмена для периода падающей скорости сушки. Используя метод графического дифференцирования кривой сушки, впервые введенный Т.К. Шервудом, А.В. Лыковым, Г.К. Филоненко, В.В. Красниковым и др. [1, 2, 3], были созданы приближенные методы расчета, основанные на наиболее общих закономерностях процесса сушки.

Качество высушиваемого материала в процессе сушки зависит от температуры и времени воздействия ее на материал. Основной причиной неравномерной объемной усадки, коробления и трещинообразования является воздействия температуры, особенно в периоде падающей скорости сушки. Важной задачей теории и практики сушки является разработка приближенных методов расчета среднеинтегральной температуры материала с минимальным количеством констант, определяемых экспериментально.

При сушке текстильных нитей для определения среднеобъемной температуры материала использовалась эмпирическая формула, относящаяся к классу дробнорациональной функции [4]

i ( т ) = F ₀ +

τao + а1т

где t( т ) - среднеинтегральная температура тела на данный момент времени; t 0 - среднеинтегральная температура в первом периоде сушки; т - текущее время, соответствующее температуре t( т ) ; а ₀ , а 1 - параметры, зависящие от температуры и влагосодержания материала.

Для существования данного вида эмпирической зависимости с двумя параметрами а ₀ и а 1 [5] и возможности ее использования для расчета среднеобъемной температуры тела в периоде падающей скорости сушки ^2тт. необходимо, чтобы среднему гармоническому значению τ ζ ^{= т} 1 + соответствовало среднее значение

2(t1-to)(tn-to) tζ=                      .

(t 1 -t 0) + (tn - t0)

Проведем выбор эмпирической формулы (1) с двумя параметрами а 0 и а 1 . На рис. 1 представлена опытная кривая t = f ( т ) при сушке пористой керамики в условиях вынужденной конвекции. Зависимость ( t- t ₀) = f ( т ) для пористой керамики представлена таблицей 1.

Таблица 1 - Зависимость ( t- t ₀) = f ( т ) для пористой керамики при режиме сушки t c =120 ^оС, ϑ =5 м/с

Х	τ , мин	3	5	8	10
Y	(t - t o ) oC	10	18	32	40

Вычисляем среднегармонические значения τζ и tζ для начальной и конечной точек.

Поскольку отклонение Δ Y ζ ₁ <  1 незначительное, то формула (1) достаточно хорошо описывает зависимость t = f ( τ ) для влажных материалов во втором периоде сушки.

Рассмотрим правило выбора параметров а 0 , а 1 и t ₀ уравнения (1)

Уравнение (1) запишем в виде:

τ t -t0 =           .

a0 + a1τ

Среднеобъемная температура влажного тела в конце первого периода сушки t0 , как показал эксперимент, близка к температуре мокрого термометра tм и меньше ее на 1-3оС для плоских влажных материалов толщиной δ ≈ 5-12 мм при различных режимах сушки.

Температура tм   определяется из уравнения теплообмена для периода постоянной скорости сушки [1]

q ₁ t_м = t_c -

α кр

rρ0RVN = tc -           ,

α кр

где r – теплота парообразования; ρ ₀ - плотность сухого тела; N –скорость сушки в первом периоде; R v – отношение объема тела к поверхности; q 1 = r ρ ₀ R_V N – плотность теплового потока в первом периоде, Вт/м² .

Коэффициенты теплообмена α для первого периода вычислялись по критериальному уравнению (4) при условии uкр < u u0 , для второго периода при uр

Nu = C ⋅ Re ^{p 0}

⎜⎛ТТс

⎝ м

\ m ₀

n

⎛u⎞

.

7

⎝uкр⎠

где \ Nu – критерий Нуссельта; С, р0, m0, n – постоянные, определяемые экспериментально; Re – число Рейнольдса; u , uкр – текущее и критическое влагосодержание материала; Тс, Т – абсолютные температуры среды и мокрого термометра; α, αкр – коэффициенты теплообмена в первом и втором периодах.

В таблице 2 даны значения параметров в уравнении (4).

Таблица 2 – Значения параметров С и n в уравнении (4)

Материал	С	n
Пористая керамика	0,75	0,5
Подошвенная кожа	0,8	0,25
Листовой асбест	0,75	0,5
Глина	0,45	0,9

Показатель степени m 0 при конвективной сушке не зависит от рода высушиваемого материала и равен m 0 = 2, а показатель степени у числа Рейнольдса p 0 = 0,5.

При обработке опытных данных по уравнению (4) за определяющую температуру принималась температура среды t c , за определяющий размер – длина поверхности влажного тела вдоль набегания потока воздуха.

Обработка экспериментов по сушке ряда влажных материалов, приведенных в таблице 2, показала линейную зависимость средней температуры t ₀ влажного материала в первом периоде от температуры t c

t0 =10 0,28⋅tc. (5)

Зависимость t ₀ = f ( t_c ) для разных материалов показана на рис.2.

Параметр а 1 уравнения (1) находится простым уравнением [4]

а1 =          .                                  (6)

t_с - t ₀

Параметр а 0 уравнения (1) по физическому смыслу выражается соотношением, которое вытекает из графического дифференцирования температурной кривой (рис.1) [4]

a0

Тогда можно записать

1

tgϕ

, где tg ϕ ⁼

⎜⎛dt ⎟⎞

⎝ dτ ⎠τ→0

а ₀

¹ = ¹

tgϕ   t1 - t0

τ 1

τ1         ⎜⎛ dt ⎟⎞     = t1-t0 , где ⎝ dτ⎠τ→0

t1

Здесь значения τ ₁ и t ₁ фиксируются при графическом дифференцировании температурной кривой t = f ( τ ) , при τ → 0 (точка 1, рис.1).

Графическое дифференцирование, как и всякий графоаналитический метод имеет погрешности, которые только увеличиваются при τ → 0 .

Поэтому провести точно касательную к точке 1 кривой t = f ( τ ) , при условии

τ → 0 (рис.1), практически невозможно, и значение t 1 параметра a ₀ является неопределенным.

Параметр a ₀ с достаточной точностью определяется совместной обработкой кривых u = f ( τ ) и температурных кривых t = f ( τ ) для периода падающей скорости сушки.

На рис.3 представлены зависимости lg a ₀ = f ( u ) и a ₀ = f ( τ ) для пористой керамики при различных режимах сушки.

Обработка и анализ опытных данных по конвективной сушке для материалов, указанных в таблице 2, дали общие уравнения для вычисления параметра a ₀ в формуле (1)

a ₀ = 0,08 ⋅ exp(10( u u_р ));                  (8)

a0 = 0,25 0,015τ,

где;

от нуля.

ы_ <« <«„

; Т - время сушки во втором периоде, отсчитываемое

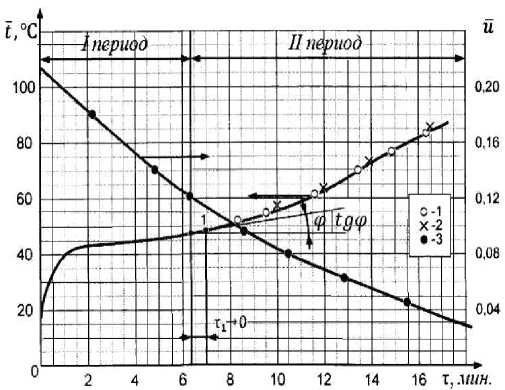
Рисунок 1 - Кривая сушки и температурная кривая при конвективной сушке пористой керамики при режиме t_c = 120 0 C , $ = 5 м/с, q = 5% : 1 - эксперимент; 2 - по формуле (1);

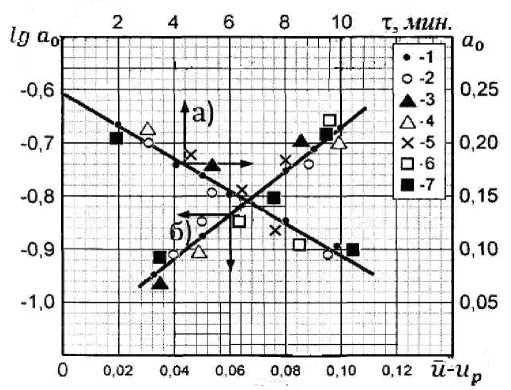
Рисунок 3 - Зависимости параметра lg o ₀ в уравнении (1) от влагосодержания и и параметра о ₀ от времени т для пористой керамики при различных режимах сушки (обозначения даны на

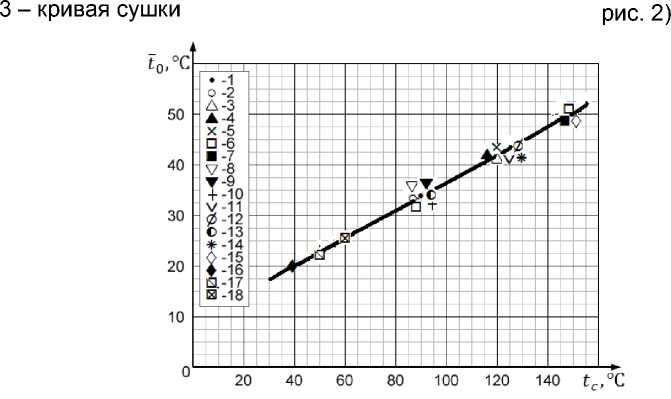
Рисунок 2 - Зависимость среднеобъемной температуры влажного материала в первом периоде Г- от температуры среды для различных влажных материалов при режимах сушки: I. Пористая керамика: 1- т.=90^:С, ^ =3м/с; 2- ;;=5м/с; 3- т.=120^:С, 5 =3м/с; 4- .—5м/с; 5- .—10м/с; 6- Т.-=150^:С, ^ =3м/с; 7- ./=5м/с. г=5мм. II. Глина: 8-

г.=90:С, ^=5м/с; 9- .?=3м/с; 10- .?=10м/с; 11-Г..=120:С, .?=3м/с; 12- .?=5м/с.

;-:=12мм. III. Асбест листовой: 13- t..=90:C, .?=5м/с; 14- L-=120:C, .?=5м/с; 15-

Г-=150:С, .?=3м/с. ё=6мм. IV. Подошвенная кожа: 16- Г..=40:С, .?=3м/с; 17- г..=50:С г=5м/с; 18- Г..=60:С, и=3м/с. :5=3мм

Результаты сравнительных расчетов среднеинтегральной температуры по уравнению (1) с экспериментом даны на рис.1. Видны достаточно надежные совпадения результатов расчета с экспериментом.

ВЫВОДЫ

Таким образом, в расчетах по кинетике сушки влажных материалов при определении среднеинтегральной температуры материала в периоде убывающей скорости сушки наряду с экспоненциальными зависимостями вида t = f (exp( mu )) можно использовать эмпирические уравнения вида (1). Результаты сравнительных расчетов среднеобъемной температуры t по уравнению (1) достаточно хорошо согласуются с экспериментальными данными.

При этом общие зависимости (5), (6) и (8), полученные в результате обработки и анализа экспериментальных данных по конвективной сушке влажных материалов для периода убывающей скорости сушки, позволяют определять среднеинтегральную температуру материала в данный момент времени по известной темпер а туре среды и заданному влагосодержанию, тогда как зависимости вида t = f (exp( mu )) требуют дополнительно знать из эксперимента первое критическое влагосодержание u _кр материала и скорость сушки в первом периоде N .