Метод расчёта дифракционного делителя пучков лазерного излучения со спектральной селекцией на основе бихромированной желатины

Целью работы является разработка методики расчёта дифракционного делителя пучка (ДДП), предназначенного для деления и фокусирования в одинаковые фокальные области освещающего пучка (или пучков) лазерного излучения, а также их селекции на три различные спектральные компоненты. В качестве источника излучения рассматривается лазерная установка, генерирующая излучение на нескольких длинах волн (RGB-лазер [1]), а носителем ДОЭ является стеклянная пластина со слоем бихромированной желатины (БХЖ).

Такой ДДП можно использовать в голографических прицелах [2], голографических индикаторах знакосимвольной информации, в оптико-электронных приборах при формировании специальных калибровочных опорных точек [3, 4]. В этих устройствах часто требуется создание многоцветных изображений, например, изображения прицельных знаков красного и зелёного цветов. Активно используются ДДП в спектрометрах в качестве диспергирующих элементов [5].

Кроме того, такие ДДП могут использоваться для создания объектного и опорного пучков в голографии и интерферометрии, формирования массива точек, для деления света на пучки с разной поляризацией, для многопучкового освещения LCD-матриц, для создания многофокусных линз, делителей фемтосекундных пучков и т.д. [6–9]. Известны такие светоделители, как куб-призма, плоскопараллельная пластинка, дифракционный светоделитель и светоделитель с плавной перестройкой коэффициента светоде-ления [10–12]. Недостатком куб-призмы и плоскопараллельной пластинки является сложность изменения коэффициента светоделения и угла дифракции лучей, а недостатком дифракционного светоделителя является невозможность регулирования соотношения энергий пучков. Недостатком светоделителя с плавным изменением коэффициента светоделения является невозможность изменения угла дифракции лучей в требуемом диапазоне. В разделе 5.4 книги [13] рассматриваются спектральные делители на основе би- нарных и многоуровневых ДОЭ (киноформ) с большой высотой ступенек, что приводит к сложностям их технологической реализации.

Для разложения света в спектр используются призмы, интерферометры Фабри–Перо и дифракционные решётки. Из-за своей высокой дисперсии дифракционные решётки получили большое распространение [6–8].

Особенностями рассматриваемого в данной статье ДДП лазерного пучка является то, что он записывается в виде объёмной голограммы, в которой угол дифракции лучей и коэффициент светоделения определяются номером матричной ячейки, на которую попал считывающий луч. В зависимости от значения коэффициента светоделения свет разлагается на 0-й и 1-й порядки дифракции. Таким образом, для RGB-лазера пучок света делится в общем случае на 6 пучков: три из них (R 0 , G 0 и B 0 ) идут в 0-й порядок дифракции, остальные 3 (R 1 , G 1 и B 1 ) идут в 1-й порядок дифракции по заданным разработчиком направлениям.

1.    Описание процесса дифракции на Брэгговских решётках в объёмной голограмме

Рассмотрим две плоские волны единичной амплитуды (рис. 1), интерференция которых наблюдается в плоскости yz [13, 14]. Согласно закону Снеллиуса sin Q„   sin Q

• - =     - = n ,                           (1)

Sin у S   Sin у R где n – показатель преломления регистрирующей среды, Qs и Qr - углы между направлениями распространения волн и осью z в воздухе, ys и ук - соответствующие углы в регистрирующей среде. Комплексная амплитуда в среде имеет вид

a(y, z) = exp[-i2n(nSy + £Sz)] + к.с., aa* = I = 2 + 2 cos { 2 n[(ns - n-)У + (5s -£-)z]}, (2) где nS = sin у s /X, ПR = sin у R /X,

^s = V1 -x2nS /X , ^- = 71 -X2n2/x

и λ – длина волны света в среде.

Полагая, что среда обладает фоточувствительностью только в плоскости z = z 1 = const, второй член в аргументе косинуса в (2) (ξ s – ξ R )z 1 в плоскости z 1 представляет собой постоянную, которую можно не

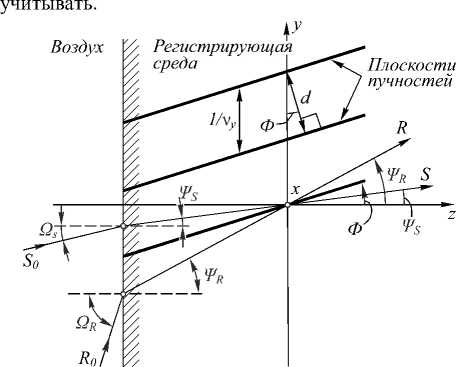
Рис. 1. Образование объёмной голограммы.

В регистрирующей среде образуются плоскости пучностей из-за интерференции световых пучков, Ω S и Ω R – углы между направлениями распространения волн и осью z в воздухе, ψ s и ψ R – соответственно углы в регистрирующей среде, d – период решётки, 1/ν y – период решётки вдоль оси y

Поверхности пучностей описываются уравнением

2 π ( η _S -η _R ) y + 2 π ( ξ _S -ξ _R ) z = con s t .            (3)

Оставшееся слагаемое соответствует фазовому члену, определяющему частоту интерференционных полос в направлении y:

ν _y = 1/ d_y =η _S -η _R = (sin ψ _S - sin ψ _R )/ λ ,        (4)

где d y – расстояние между соседними максимумами распределения интенсивности в направлении y.

Угол ϕ между плоскостью пучностей и осью z определяется с помощью дифференцирования по z (3)

(ηS -ηR)dy+(ξS -ξR)=0, dz tgφ =dy =-ξS-ξR .                           (5)

dz    η _S -η _R

Преобразовав (5), получим

, _ V 1 - sin ψS - V1-sin2ψR tgφ = - sinψS -sinψR

= tg ( ^{ψ S +} 2 ^{ψ R} ).(6)

Таким образом, поверхности пучностей элементарной голограммы делят пополам угол между волновыми векторами интерферирующих волн.

Перейдя к углу θ, которым обозначается угол между пучком и плоскостью пучностей в среде, получим d = dy cos φ

cos φ η _S -η _R

На рис. 2 показано поперечное сечение элементарной объёмной голограммы [14]. В таких объёмных голограммах каждый луч последовательно рассеивается от большого числа периодически расположенных максимумов плотности среды. Так как рассеянные волны интерферируют, для исключения их затухания они должны быть синфазны.

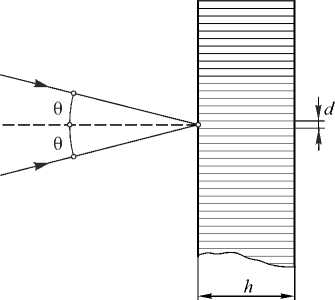
Рис. 2. Схема записи объёмной голограммы. Вследствие интерференции двух пучков света в среде образуются плоскости пучностей, θ – угол между лучом и нормалью к поверхности, h – толщина фотоносителя, d – период голограммы

Пропускание голограммы зависит от длины волны света и угла падения интерферирующих пучков, коэффициент светоделения определяется временем экспонирования, а угол дифракции определяется формулой Брэгга (рис. 2) [14].

2 d sin θ = λ In ,                                   (8)

где d – период решётки, θ – угол между пучком и плоскостью пучностей в светочувствительной среде, λ – длина волны в воздухе, n – средний показатель преломления в среде.

Чтобы можно было варьировать угол дифракции лучей и коэффициент светоделения (на соответствующих длинах волн), можно записать матрицу объёмных субголограмм, например, как это показано на рис. 3.

Угол отклонения луча
60°	1,1	1,2	1,3	1,4	1,5
55°	2,1	2,2	2,3	2,4	2.5
50°	3,1	3,2	3,3	3,4	3,4
45°	4,1	4,2	4,3	4.4	4.5
	20%	40%	60%>	80%	100%

Коэффициент светоделения

Рис. 3. Матрица объёмных субголограмм

Оценим амплитуду S(T) прошедшей через объёмную субголограмму волны. Для диэлектрической фазовой решётки без потерь введём параметры

ζ=δβ T sin θ ₀ = ГT /2cos θ ₀ , (9)

ν = χ T /2cos θ ₀ = π n ₁ TJ 2cos θ ₀ , (10) где Г = δβ sin2 θ 0 , δ – малое отклонение от θ , β = 2 π n / λ , χ – постоянная взаимодействия, T – толщина голограммы, n 1 – показатель преломления фоточувстви-тельной среды.

Амплитуда прошедшей волны равна

S ( T ) =- i

exp( - i ζ ) sin л] ζ ² +ν ²

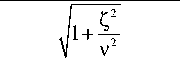
Полагая, что амплитуда падающей волны равна 1 при z=0 [14], дифракционная эффективность голограммы определяется соотношением

η=

| S ( T ) |² | R (0) |²

= | S ( T ) |² .

Рассмотрим случай падения под углом Брэгга полагая, что δ =0 и ζ =0. Эффективность будет равна 1, если sin ν = 1 или

πn Tπ

ν= 1

λ cos θ ₀ 2

Другая форма записи nT λ

ν= 1

cos θ ₀ 2

(13 а )

Левая часть равенства (13) эквивалентна приращению оптического пути падающего луча, наблюдаемого в случае, если бы среднее изменение показателя преломления среды голограммы равнялось n1. Ес- ли эквивалентное изменение длины пути равно половине длины волны падающего излучения (в воздухе), то дифракционная эффективность теоретически будет равна 100 %. Однако при угле падения, отличном от угла Брэгга, величина дифракционной эффективности резко уменьшается, что показано на рис. 4.

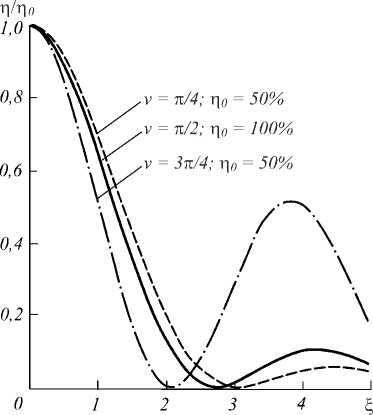
Рис. 4. Зависимость относительной дифракционной эффективности η/η 0 пропускающей объёмной субголограммы от параметра ζ = δ(2πn/λ)Tsinθ 0 для различных значений параметра ν = πn 1 T/λ cos θ 0

По вертикальной оси отложена относительная дифракционная эффективность η/η0 объёмной субголограммы, а по горизонтальной оси указано отклонение δ от угла Брэгга. Каждая из трёх кривых соответству- ет модуляционным параметрам ν, равным соответственно π/2, π/4 и 3π/4.

2.    Схемы получения дифракционного делителя пучка в виде матрицы объёмных субголограмм

Для получения итогового ДДП нужно использовать оптическую схему записи матрицы объёмных субголограмм (рис. 5), в которой объектная волна проходит через вспомогательный транспарант (амплитудный или фазовый) с дифракционными решётками, направляющими продифрагировавшие пучки излучения в требуемые зоны-ячейки будущей матрицы объёмных субголограмм (рис. 3), и падает под требуемым углом на фотопластинку для записи мат-

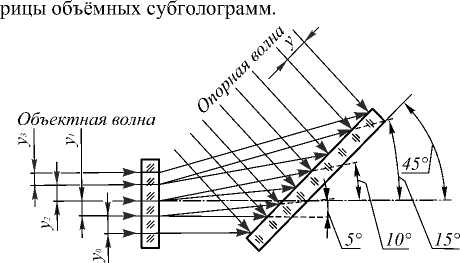
Рис. 5. Запись голограммы. Для записи используется

технологическая матрица голограмм, отклоняющая пучки на 0°, 5°, 10° и 15° соответственно. Для снижения требований к технологической голограмме заготовка повёрнута на 45°

Причём опорная волна падает на фотопластинку по нормали, а сама фотопластинка повёрнута на 45° к оптической оси. Это сделано для того, чтобы увеличить период интерференционных полос при записи. Чтобы изменять при записи коэффициент светоделе-ния, можно воспользоваться специализированным клином с переменным коэффициентом пропускания (на рисунке не показан) или изменять время экспозиции участков в матрице объёмных субголограмм.

Запись матрицы объёмных субголограмм выполняется на трёх длинах волн используемого RGB-лазера, однако для каждой матрицы используется свой амплитудный транспарант.

Схема восстановления пучков лазерного излучения на разных длинах волн с одной ячейки матрицы объёмных субголограмм представлена на рис. 6. Пучок излучения от RGB-лазера падает на соответствующую ячейку матрицы субголограмм, дифрагирует на ней и разделяется (отклоняется) в зависимости от того, на какую ячейку он попал. На рис. 6а показано прохождение монохроматического пучка света в 1-й порядок дифракции. На рис. 6б показан вариант дифракции света при освещении ячейки матрицы субголограмм одновременно тремя пучками на различных длинах волн от RGB-лазера. Каждый вариант штриховки соответствует своему пучку лазерного излучения на соответствующей длине волны. Пучки лазерного излучения всех цветов проходят в 0-й порядок с различной интенсивностью, а в 1-м порядке дифракции лазерные пучки с различными длинами волн отклоняются каждый в свою сторону. Относительная интенсивность излучения на различных длинах волн в 0-м и 1-м порядках определяется дифракционной эффективностью и другими параметрами каждой ячейки в матрице субголограмм.

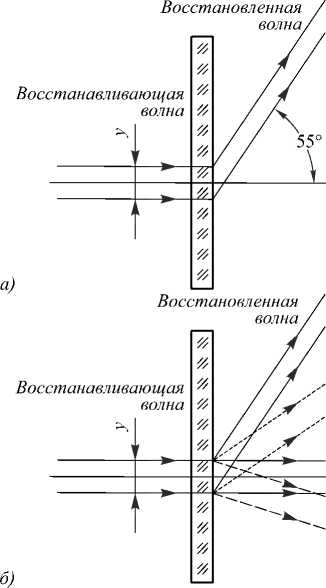
Рис. 6. Схемы дифракции лазерного излучения на одиночной ячейке матрицы объёмных субголограмм, где а) отклонение пучка лазерного излучения на одной длине волны в 1-й порядок дифракции; б) отклонение трёх пучков лазерного излучения на трёх длинах волн также в 1-й порядок дифракции

Тогда период дифракционных решёток внутри ДДП, выполненного на основе фотопластинки БХЖ, равен dk =X(sm^ж .                               (16)

4.    Результаты расчётов основных параметров дифракционного делителя пучка

Для оценки требуемых параметров вспомогательного транспаранта в табл. 1 и 2 приведены примеры расчётов для матрицы дифракционных решёток, отклоняющих красный, зелёный и синий луч соответственно. На рис. 3 была приведена карта матрицы объёмных субголограмм (будущего ДДП), а на рис. 5 – процесс записи матрицы объёмных субголограмм для синих, зелёных либо красных пучков лазерного излучения. Так как отклонение синего, зелёного и красного пучков планировалось в одну и ту же сторону для отдельно взятой ячейки, то схемы процессов записи в этом примере совпадают. На рис. 6 а показана работа ячейки в строке 2.

Табл. 1. Значения параметров дифракционных решёток на вспомогательном транспаранте и для отдельных субголограмм в матрице для длины волны λ кр = 650 нм

Номер участка	0	1	2	3
Угол дифракции, град	45°	50°	55°	60°
Длина участка вспомогательного транспаранта, мм	1,56	3,42	1,1	1,1
Период дифракционных решёток на вспомогательном транспаранте, мкм	-	7,46	3,74	2,51
Период дифракционных решёток на субголограмме, записанной на БХЖ, мкм	0,92	0,85	0,79	0,75

Табл. 2. Значения параметров дифракционных решёток на вспомогательном транспаранте и для отдельных субголограмм в матрице для длины волны λ з = 555 нм

Номер участка	0	1	2	3
Угол дифракции, град	45°	50°	55°	60°
Длина участка вспомогательного транспаранта, мм	1,56	3,42	1,1	1,1
Период дифракционных решёток на вспомогательном транспаранте, мкм	-	6,37	3,20	2,14
Период дифракционных решёток на субголограмме, записанной на БХЖ, мкм	0,78	0,72	0,68	0,64

Табл. 3. Значения параметров технического ДОЭ и ДОЭ на БХЖ для длины волны λ с = 441 нм

Номер участка	0	1	2	3
Угол дифракции, град	45°	50°	55°	60°
Длина участка вспомогательного транспаранта, мм	1,56	3,42	1,1	1,1
Период дифракционных решёток на вспомогательном транспаранте, мкм	- TO	5,06	2,54	1,70
Период дифракционных решёток на субголограмме, записанной на БХЖ, мкм	0,62	0,58	0,54	0,51

Выводы

Приведена методика расчёта дифракционного делителя пучков лазерного излучения со спектральной селекцией, выполненного в виде матрицы объёмных субголограмм, записанных на фотопластинках с би-хромированной желатиной. Дан пример расчёта основных параметров матрицы субголограмм, рассмот- рены схема записи матрицы объёмных субголограмм и схема дифракции пучков лазерного излучения на трёх длинах волн работы при использовании RGB-лазера. Расчёт проведён для углов дифракции, равных 45°, 50°, 55° и 60°, при падении пучков лазерного излучения на трёх длинах волн, приведён вариант создания дифракционной ячейки для деления компонент светового пучка по амплитуде на 0-й и 1-й порядки дифракции и в зависимости от длины волны излучения. Данная методика расчётов позволяет усовершенствовать голограммные и дифракционных оптические элементы, используемые в голографических прицелах и индикаторах знако-символьной информации, при формировании в них многоцветных изображений, например, изображений прицельных знаков красного и зелёного цветов.

Авторы предполагают в последующей работе провести цикл соответствующих экспериментальных исследований по изготовлению такого ДДП для RGB-лазера и надеются подтвердить полученные расчётные параметры.

Данная работа выполнена в МГТУ им. Н.Э. Баумана при финансовой поддержке Минобрнауки РФ в рамках соглашения №14.577.21.0115 (идентификатор проекта RFMEFI57714X0115).