Метод расчёта параметров математической модели судна

• 1.    Введение

• 2.    Расчёт параметров математической модели судна

  Для определения параметров модели (1) воспользуемся известной из работы Г.В. Соболева (1976) зависимостью между угловой скоростью судна a на циркуляции и углом перекладки руля a r

Использование математических моделей судна для решения практических задач судовождения становится всё более актуальным, что вызвано, прежде всего, использованием современных компьютерных технологий в судовых навигационных системах, а также инновационных методов и способов управления судном при выполнении ключевых судовых операций в условиях повышенных рисков. В связи с этим, ИМО (Международная морская организация) разработала и приняла известную резолюцию А.751(18), подтверждающую необходимость использования математических моделей судна при решении практических задач, лежащих в области безопасности судовождения.

Известно, что XIV Международной конференцией опытовых бассейнов рекомендована для практического использования относительно простая, но в известной степени приемлемая для решения ряда прикладных задач судовождения математическая модель судна

T 1 T 2 ( d² a / dt ²) + ( T 1 + T 2 )( d a /dt ) + a + H( a ) = K a r + KT з ( d a / dt ),                 (1)

где H ( a ) = v 1 | a | a + v ₂ a ³; Т 1 , Т 2 , Т 3 , К , v 1 , v ₂ - параметры математической модели; a - угловая скорость судна; a r - угол перекладки руля.

В данной работе представлен один из методов определения параметров указанной модели, построенный на основе результатов исследований, опубликованных в целом ряде работ хорошо известных в области теории корабля авторов Е.Б. Юдина, А.П. Тумашика, Г.В. Соболева (1976), Р.Я. Першица (1983).

v 2 a + v 1 | a | a + a = K a r ,                                        (2)

которая по сути является уравнением кубической параболы, проходящей через начало координатной системы a _r , a .

Чтобы определить значения коэффициентов V 1 , v ₂, К выполним следующие преобразования:

• - разделим обе части уравнения (2) на величину K a , получим

• v2aK + v11 a | / K + 1/K = ar /a;(3)

  – введём обозначения

a 1 = 1/K;     a 2 = V1/K;    a 3 = v2/K.(4)

С учётом введённых обозначений уравнение (2) примет вид a3a + a2a + a 1 = ar/a.(5)

Используя результаты натурных испытаний, строим график зависимости a = f ( a r ), который в теории корабля носит название диаграммы управляемости. При этом размерность угловой скорости a рад/с, а размерность угла перекладки руля a r в радианах.

Юдин Ю.И. и др. Метод расчёта параметров математической модели судна

Выбрав ряд значений угловой скорости ω i c интервалом ∆ ω , соответствующих определённым значениям угла перекладки руля α ri определяем соотношения α ri / ω i . Величина интервала ∆ ω выбирается с учётом желаемой точности значений коэффициентов ν 1 , ν 2 , К . Используя значения ω max = 0,02553 и ω min = –0,02551, снятые с построенной по результатам натурного эксперимента диаграммы управляемости, и установив количество интервалов равное n = 31, получим значение ∆ ω = 0,00165.

Определим значения соотношения α _r / ω в двух соседних точках:

αri+1/ωi+1= a3ω2i+1 + a2 I ωi+1 I + a1,(6)

αri/ωi = a3ωI2 + a2|ωi| + a1.(7)

Вычитая (7) из (6), получим

αri +1/ωi+1 – αri/ωi = a3(ω2i+1– ωi2) + a2(|ωi+1| – |ωi|).(8)

Учтя, что

ω ² i +1 – ω ² i +1 = ( ω i +1 – ω i )( ω i +1 + ω i ) = ∆ ω (2 ω i + ∆ ω ),

| ω i +1 | – | ω i | = ∆ ω , из (8) получим следующее равенство:

α ri +1 / ω i +1 – α r i / ω i = a 3 ∆ ω (2 ω i + ∆ ω ) + a 2 ∆ ω .                              (9)

Введя обозначения:

а = а3∆ω; b = а2∆ω; yi = αri+1/ωi+i – αri/ωI; xi = 2ωi + ∆ω, равенство (9) представим в виде yi = а xi + b.                                                  (10)

Известный набор значений х i , y i ( i = 1, 2, 3, …, n -1) определяется с использованием результатов натурного эксперимента, представленных в виде диаграммы управляемости. Коэффициенты линейной аппроксимации a , b определяются с помощью метода К. Гаусса, согласно которому

₌ xy - x × y _; x ² - ( x ) ²

n - 1

b = y - ax ; x = ( ) ∑ x_i ; ⁿ i = 0

n - 1

y = ( ) ∑ y_i ;

ⁿ i = 1

n - 1

₁ n - 1 xy = ( ) ∑ x_iy_i .

n i = 1

2 x

= (¹) ∑ x i ² ;

ⁿ i = 0

Таким образом, используя выражения (11), с учётом данных, полученных при выполнении натурного эксперимента, будем иметь:

х = 1,8166∙10^-5; у = -4,7099∙10^-4; х = 8,6772∙10^-4; ху = 2,0950∙10^-2, а = 24,144; b = -9,0960∙10^-4.

С учётом введённых ранее обозначений, находим а3 = а/∆ω = 14662;      а2 = b/∆ω = -0,55237.

Пользуясь выражением (5), получим равенство для определения значения коэффициента а1 a1 = αr i / ωi – a3 ωi – a2 |ωi|.(12)

Просуммируем обе части равенства (12) по i = 0, 1, 2, …, n-1: n-1

∑ a1 = ∑ [(αri/ωi) – a3/ω2i – a2|ωi|].(13)

i=0

Используя правила суммирования, преобразуем равенство (13) к виду n-1                    n-1

a1 = ∑ (αri/ωi) – a3∑ ω2i – a2∑ |ωi|,(14)

i=0                      i=0

откуда n-1                    n-1

a1 = (1/n) [ ∑ (αri/ωi) – a3∑ ω2i – a2∑ |ωi|].(15)

i=0                    i=0

Учитывая значения коэффициентов а ₂, а ₃ из (15), находим а ₁ = 10,969, а используя выражения

(4), определяем искомые коэффициенты: К = 0,91163; ν ₁ = 1,10345; ν ₂ = -0,98055.

На рис. 1 представлена диаграмма управляемости, построенная по результатам натурного эксперимента и рассчитанная с использованием полученных значений коэффициентов К , ν ₁, ν ₂.

Вестник МГТУ, том 12, №1, 2009 г.   стр.5-9

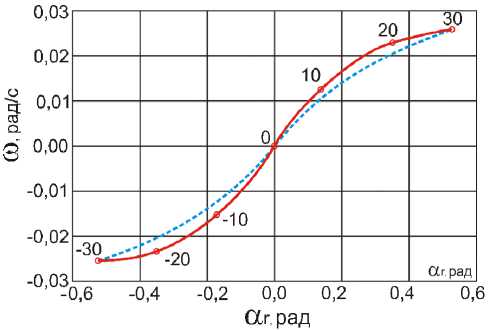
Рис. 1. Экспериментальная кривая и кубическая парабола, определяемая коэффициентами К , ν 1 , ν 2

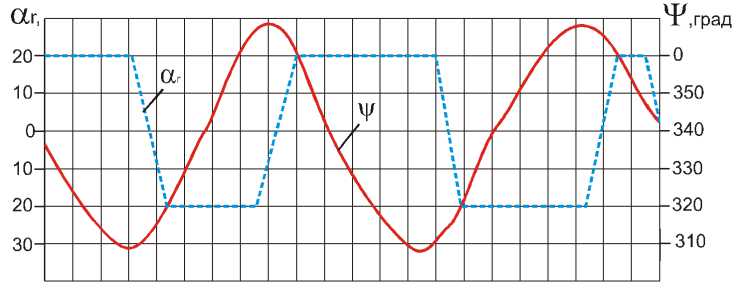
Рис. 2. Изменение угла перекладки руля α _r и курса судна ψ при выполнении манёвра "Зигзаг" (натурный эксперимент)

Обозначим через t k время выполнения манёвра "Зигзаг". Для определения значений коэффициентов Т ₁, Т ₂, Т ₃ воспользуемся графическим представлением результатов выполнения манёвра "Зигзаг". В качестве примера здесь и ранее используются результаты натурного эксперимента, выполненного на рыболовном траулере проекта 394-АМ. Характер изменения угла перекладки руля и курса судна при выполнении манёвра "Зигзаг" показан на примере одного из выполненных в ходе натурного эксперимента манёвров (рис. 2).

С целью использования кривой ψ ( t ) в дальнейших расчётах следует располагать ее аналитическим представлением. Оптимальной для этого представляется квадратичная функция, в виде совокупности нескольких парабол с переменными числовыми значениями коэффициентов, которые обозначим следующим образом: аⁱ_р , bⁱ_р , сⁱ_р , i = 1, 2, 3, …, n – количество парабол. Тогда общий вид квадратичной параболы будет выглядеть так

ψ = aⁱ p t ² + bⁱ p t + cⁱ p .                                               (16)

Для i-ой параболы, проведённой через три экспериментальные точки (t2i, ψ2i); (t2i+1, ψ2i+1); (t2i+2, ψ2i+2), i = 1, 2, …, n-1, значения коэффициентов определяются из условия aipt22i + bipt2i + cip = ψ2i;

a p^t 2 i + 1 ⁺ b p^t 2 i + 1 ⁺ c p ⁼ ψ 2 i + 1 ;                                           (17)

aⁱ p^{t 2} 2 i + 2 ⁺ bⁱ p^t 2 i + 2 ⁺ cⁱ p ⁼ ψ 2 i + 2^.

Таким образом, любое значение курса судна ψ при заданном значении времени 0 ≤ t ≤ t k определяется в два этапа: на первом этапе для заданного значения i определяются значения коэффициентов аⁱ_р , bⁱ_р , сⁱ_р ; на втором этапе для выбранного значения времени t из условия t _{2 i} ≤ t ≤ t _{2 i +1} по формуле (16) вычисляется необходимое значение ψ . Расчёт угловой скорости для заданного значения времени t выполняется на основании известной зависимости ω = d ψ / dt , использование которой с учётом уравнения (16) приводит к выражению

ω = d ψ / dt = 2 aⁱ p t + bⁱ p .                                      (18)

Так как кинематические параметры движения судна во время выполнения манёвра "Зигзаг" определялись с начальными условиями: t = 0; ω = 0; ψ = 0; α _r = 0, вычисление значений коэффициентов Т 1 , Т 2 , Т 3 выстраивается в виде следующего алгоритма ( Ship theory handbook , 1985).

Проинтегрировав уравнение (1) при указанных начальных условиях, получим k1dω/dt + k2ω + ∫(ω – ν1|ω|ω + ν2ω3 – Kαr)dt – k3αr = 0.                      (19)

С учётом параметров, входящих в уравнение (1), очевидно, что k1 = T1T2; k2 = T1 + T2; k3 = KT3.                                      (20)

Чтобы найти коэффициенты k ₁, k ₂, k ₃, необходимо ещё раз проинтегрировать уравнение (19). Меняя трижды пределы интегрирования, получим необходимое количество уравнений. Пределами интегрирования выбираются заданные моменты условного окончания манёвра "Зигзаг" t k 1 , t k 2 , t k 3 , а необходимые для определения значений коэффициентов k ₁, k ₂, k ₃ уравнения будут иметь следующий вид:

tki

k 1 ω tki + k 2 ψ tki +

∫

tki

( ω – ν 1 | ω | ω + ν 2 ω ³ – K α r ) dtdt – k 3 ∫ α r dt = 0.

Юдин Ю.И. и др. Метод расчёта параметров математической модели судна

Использование данного метода расчёта требует существенного увеличения времени на проведение натурного эксперимента, т.к. увеличивает количество периодов колебательного движения судна при выполнении манёвра "Зигзаг" примерно в три раза. Поэтому, на наш взгляд, следует прибегнуть к использованию иного расчётного метода, необходимым условием реализации которого является выполнение не менее двух периодов колебательного движения судна при осуществлении манёвра "Зигзаг".

Для вычисления значений коэффициентов k ₁, k ₂, к ₃ необходимо решить систему дифференциальных уравнений, полученных с использованием слагаемых уравнения (19) и условно вводимых моделирующих функций F ₁, F ₂, F ₃. Система уравнений с учётом сказанного выглядит следующим образом:

dW / dt = v ₂ to ³ + v ₁ | to | to + to — K a r ;

dN ₁ i I dt = to F i ;

dN ₂ i Idt = a r F i ;                                              (22)

dN ₃ i Idt = Ф F i .

Из сказанного выше очевидно, что i = 1, 2, 3, а временной интервал интегрирования ограничен значением времени окончания выполнения манёвра "Зигзаг", т.е. 0 <  t <  t k .

Моделирующие функции F_ь F ₂, F ₃ зададим следующим образом (рис. 3):

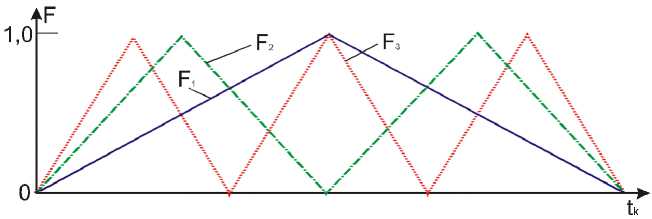
Рис. 3.

Графическое представление моделирующих функций

F 1 =	2 11 t k ,      0 < t < t k I2;                        2 — 2 11 t k ,      t I2< t < t k ;
F 2 =	4 11 t k ,      0 < t < t k I4;                        2 — 4 11 t k ,      t k I4< t <  t k I2; 4 11 t k — 2,   t k I2< t <  3 t k I4;                  4 — 4 11 t k ,     3 t k I4 <  t <  t k ; , ,         .       „                     „ , ,          „        _                     (23) 6 11 tk ,       0 < t <  tk I6;                       2 — 6 11 tk ,       tk I6 <  t <  tk I3;
F 3 =	6 11 t k — 2,    t k I3< t <  t k I2;                  4 — 6 11 t k ,      t k I2 <  t <  2 t k I3; 6 11 t k — 4,  2 tk I3 <  t <  5 tk I6;               6 — 6 11 t k ,     5 tk I6 <  t <  tk

Система уравнений (22), при начальных условиях t = 0, to = 0, a r = 0, W = 0, N ji = 0, решается методом Рунге-Кутта, обобщённым для решения систем. Для обеспечения высокой точности при решении системы интервал интегрирования 0 <  t <  t k был разбит на m = 5000 равных частей. В результате решения с использованием результатов натурного эксперимента и рассчитанных ранее значений коэффициентов v ₁, v ₂, К получены следующие значения искомых переменных:

W ( t k ) = 0,086115;

N 21 ( t k ) = 0,44398; N 31 ( t k ) = 20,565;

N _н( t k ) = -0,044870;

N 22 ( t k ) = -15,677;

N 32 ( t k ) = 37,288;

N 12 ( t k ) = -0,58422;

N 23 ( t k ) = -7,4253; N 33 ( t k ) = 27,230.

N 13 ( t k ) = -0,33484

Значения коэффициентов k ь k2, k3 определяются из системы трёх линейных уравнений k 1A1 + k2N11 — k3N21 = -N31;

k 1 A 2 + k 2 N 12 — k 3 N 22 = - N 32 ;        (24)

k 1A 3 + k2 N13 — k3 N23 = - N33, составленных с учётом численных значений вспомогательной функции Ai(tk), i = 1, 2, 3. Аналитическое выражение функциональных зависимостей Ai(tk) вытекает из рис. 4.

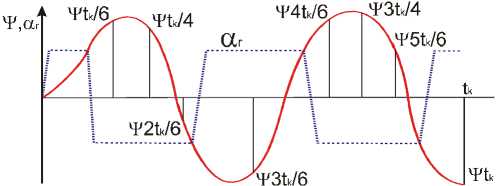
Рис. 4. Схема изменения курса у и угла перекладки руля а г при выполнении манёвра "Зигзаг"

А 1 = 2[ ^ ( t k I2) — у ( t k )] t-¹ k ;

А 2 = 4[ ^ ( t k ) — 2 ^ (3 t k I4) + 2 у ( t k I2) — 2 ^ ( t k I4)] t"* k ;                                         (25)

A 3 = 6[ y ( t k ) — 2 ^ (5 t k I6) + 2 ^ (4 t k I6) — 2 < 3 t k I6) + 2 ^ (2 t k I6) — 2 ^ ( t k I6)] t"* k .

Вестник МГТУ, том 12, №1, 2009 г.   стр.5-9

В нашем случае, значения функций А_i ( t_k ) и k ₁, k ₂, k ₃ будут следующими:

А 1 = -3,6744 ∙10^-4;     А 2 = -6,2625 ∙10^-2;     А 3 = -2,2123 ∙10^-2;

k 1 = 1139,2;             k 2 = 312,34;            k 3 = 13,812.

Используя очевидные соотношения, представленные зависимостями (20), находим значения коэффициентов уравнения (1) по формулам:

T 1 = 0,5 k 2 + (sign k 2 )[(0,5 k 2 )²– k 1 ]^0,5;

T 2 = 0,5 k 2 – (sign k 2 )[(0,5 k 2 )² – k 1 ]^0,5;                                  (26)

T 3 = k 3 / K .

Итак, Т 1 = 0,103; Т 2 = 3,691; Т 3 = 1,515.

Для оценки адекватности полученных значений параметров математической модели рыболовного траулера проекта 394-АМ ( ν 1 , ν 2 , К , Т 1 , Т 2 , Т 3 ) выполнен их расчёт c использованием известных теоретических зависимостей ( Першиц , 1983). Результаты расчёта представлены в таблице.

Таблица

Параметры математической модели судна полученные:	K	ν 1	ν 2	T 1	T 2	T 3
с использованием данных натурного эксперимента	0,911	1,103	-0,981	0,103	3,691	1,515
с использованием теоретических зависимостей	1,090	1,555	-0,834	0,186	2,163	0,918

3. Заключение

Представленный в работе метод расчёта параметров математической модели судна с использованием результатов натурного эксперимента, позволяет рекомендовать его для идентификации математических моделей различных типов судов. При этом необходимо учитывать, что область использования рассмотренной математической модели судна имеет определённые ограничения, т.е. она может быть использована для моделирования слабых манёвров. Кроме того, необходимо учитывать, что параметры представленной модели зависят от скорости судна.