Метод расчёта преломляющего оптического элемента, формирующего заданные распределения освещённости и волновой фронт
Автор: Досколович Леонид Леонидович, Быков Дмитрий Александрович, Мингазов Альберт Айдарович, Безус Евгений Анатольевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 6 т.45, 2021 года.
Бесплатный доступ
В приближении геометрической оптики рассмотрен метод расчёта преломляющего оптического элемента с двумя рабочими поверхностями, преобразующего падающий пучок с плоским волновым фронтом в выходной пучок, формирующий заданное распределение освещённости и заданный волновой фронт. Приведены примеры расчёта оптических элементов, формирующих заданные распределения освещённости и сферические волновые фронты (сходящиеся и расходящиеся гомоцентрические пучки). Представленные примеры демонстрируют хорошие рабочие характеристики метода.
Преломляющая поверхность свободной формы, геометрическая оптика, обратная задача, освещённость, волновой фронт
Короткий адрес: https://sciup.org/140290279
IDR: 140290279 | DOI: 10.18287/2412-6179-CO-912
Текст научной статьи Метод расчёта преломляющего оптического элемента, формирующего заданные распределения освещённости и волновой фронт
Задача расчёта оптических элементов с поверхностями свободной формы (от англ. freeform ), формирующих заданные распределения освещённости и заданные волновые фронты, имеет множество практических приложений, включающих дизайн систем освещения и подсветки, формирование лазерных пучков заданной формы, в т.ч. в системах литографии, лазерной печати, оптической памяти и т.п. [1, 2]. Одновременный контроль распределения освещённости и волнового фронта требует использования оптического элемента с двумя «рабочими» поверхностями (преломляющими или отражающими).
В приближении геометрической оптики задача расчёта оптического элемента, формирующего заданные распределение освещённости и волновой фронт, может быть сведена к решению нелинейного дифференциального уравнения (НДУ) эллиптического типа [3–9]. Несмотря на то, что для решения данного НДУ были предложены различные конечно-разностные методы [3–9], расчёт оптических элементов в рамках такого подхода является сложным и имеет ограничения. В частности, формулировка задачи расчёта оптического элемента в виде НДУ предполагает, что рассчитываемые поверхности оптического элемента являются гладкими. Требование гладкости ограничивает класс распределений освещённости, которые могут быть сформированы оптическим элементом. Например, оптический элемент с гладкими поверхно- стями не позволяет сформировать распределение освещённости, определённое в несвязной области, или в области с негладкими границами [10, 11].
В частном случае т.н. задачи «коллимированного» формирования светового пучка (от англ. collimated beam shaping ), когда волновые фронты падающего и выходного пучка являются плоскими, задача расчёта оптического элемента может быть сформулирована как задача Монжа–Канторовича о перемещении масс (ЗПМ) [10–12]. Данная ЗПМ описывает расчёт интегрируемого лучевого отображения (т.е. отображения, связывающего координаты падающих на оптический элемент лучей и координаты преломлённых (отражённых) лучей в выходной плоскости), которое обеспечивает заданное распределение освещённости. Расчёт оптического элемента в рамках «ЗПМ-формулировки» может быть сведён к решению задачи линейного программирования [11] или линейной задачи о назначениях [10]. ЗПМ-формулировка задачи, в отличие от задачи решения НДУ, позволяет рассчитывать оптические элементы с непрерывными, кусочно-гладкими поверхностями. Это позволяет формировать распределения освещённости, заданные в несвязных областях и в областях со сложными и негладкими границами [10, 11]. Тем не менее, когда волновой фронт входного или выходного пучка не является плоским, задача расчёта оптического элемента уже не может быть сведена к ЗПМ, так что методы [10, 11] становятся неприменимыми.
Одним из методов, широко используемых для расчёта отражающих и преломляющих поверхностей, является метод опорных квадрик (МОК) [13–19]. Основными достоинствами МОК являются его универсальность и простота. В рамках метода требуемое распределение освещённости приближается дискретным распределением, заданным в конечном числе N точек. Далее оптическая поверхность представляется в виде набора N фрагментов квадрик, фокусирующих падающий пучок в требуемых точках. В зависимости от задачи в качестве квадрик используются параболоиды, эллипсоиды, гиперболоиды или более сложные поверхности, например, картезианские овалы [17]. В частности, в задаче расчёта зеркала для формирования заданного дискретного распределения освещённости в ближней зоне поверхность зеркала представляется в виде набора сегментов эллипсоидов, у которых один фокус совпадает с источником излучения, а другой – с одной из точек формируемого дискретного распределения. Расчёт параметров квадрик осуществляется итерационным методом, при этом в упомянутой выше задаче расчёта зеркала сходимость метода строго доказана [14].
В недавней работе [20] авторов данной статьи был рассмотрен вариант МОК в задаче коллимированного формирования светового пучка, т.е. когда волновые фронты падающего и выходного пучка являются плоскими. При этом было показано, что предложенный вариант МОК является методом градиентного спуска для максимизации вогнутой функции, являющейся дискретным аналогом функционала Лагранжа в задаче перемещения масс. В данной статье мы рассматриваем МОК в более общем случае, когда волновой фронт выходного пучка не является плоским и задаётся через функцию эйконала в выходной плоскости. Аналогично [20], предлагаемый метод является простым в реализации и основан всего на нескольких базовых формулах. Предложенный метод проиллюстрирован примерами расчёта оптических элементов, демонстрирующими хорошие рабочие характеристики метода. Представленные примеры показывают возможность расчёта оптических элементов, формирующих выходные пучки со сферическими волновыми фронтами (расходящиеся и сходящиеся гомоцентрические пучки) и обеспечивающих заданные распределения освещённости, в т.ч. требуемые распределения освещённости, заданные в двухсвязной области.
1. Постановка задачи
Рассмотрим трёхмерное пространство Е 3 с координатами ( x 1 , x 2 , z ). Пусть на оптический элемент с двумя преломляющими поверхностями падает световой пучок с плоским волновым фронтом, параллельным плоскости z =0, при этом пучок формирует в указанной плоскости распределение освещённости I( x ), x = ( x 1 , x 2 ) e G и (рис. 1 а ). Первая поверхность R 1
задаётся функцией z = и 1 ( x ), x e G . Вторую поверхность R 2 будет удобно определить относительно некоторой «выходной» плоскости z = f >0, расположенной за элементом. В этой плоскости будут заданы распределение освещённости и функция эйконала, формируемые оптическим пучком, прошедшим через оптический элемент (рис. 1 а ). Обозначим y = ( y 1 , y 2 ) декартовы координаты в плоскости z = f . Функция эйконала ^ ( y ), y e D , задаёт требуемый волновой фронт выходного пучка и определяет направления лучей в плоскости z = f в виде
p ( y ) = ( P x , ( У ), P x 2 ( y ), P z ( y ) ) =
= -(vT ( y ), J n 0 -||V^ ( y )||21
n 0 V J
где p ( y ) - единичный вектор луча (здесь и далее стрелками обозначаются трёхмерные векторы),
W( y ) =
d^ ( y ) d^ ( y ) d y , , d y 2
|| « || - евклидова норма, n 0 - показатель преломления среды вне элемента. Далее будем считать, что показатель преломления элемента (т.е. показатель преломления среды в области между поверхностями R 1 , R 2 ) равен n 1 > n 0 .
Поскольку направления лучей в плоскости z = f должны совпадать с направлениями лучей, преломлённых второй поверхностью R 2 , то определим вторую поверхность через функцию l ( y ), равную расстоянию вдоль направления луча от второй поверхности до плоскости z = f (рис. 1 а ). В этом случае вторая поверхность может быть представлена в следующем параметрическом виде:
Z? 2( y ) = ( u 2, x , ( y ), u 2, x 2 ( y ), u 2, z ( y ) ) =
= ( y , f )- p ( y ) l ( y ) =
= ( У 1 - P x , ( y ) l ( y ) , y 2 - P x 2 ( y ) l ( y ) , f - P z ( y ) l ( y ) ) .
Луч, выходящий из точки x e G плоскости z = 0, последовательно преломляется на поверхностях R 1 , R 2 и попадает в некоторую точку y в выходной плоскости z = f (рис. 1 а ). Таким образом, поверхности R 1 , R 2 задают лучевое отображение y = у ( x ), определяющее координаты преломленных лучей в выходной плоскости через координаты падающих лучей. Это отображение задаёт распределение освещённости L ( y ), формируемое в плоскости z = f . Данное распределение определяется из закона сохранения светового потока:
L ( y ( x ) ) = I ( x )/ J у ( x ), (3)
где J ^ ( x ) - якобиан отображения у . Закон сохранения светового потока может быть также записан в интегральной форме:
J I ( x )d x = J L ( y )d y , (4)
-
Y- 1 ( B ) B
где B – произвольное подмножество в выходной плоскости.
Задача формирования заданного распределения освещённости и волнового фронта, которую мы рассматриваем в данной статье, формулируется следующим образом. Пусть заданы распределение освещённо- сти I(x), x e G, формируемое в плоскости z=0 падающим пучком с плоским волновым фронтом, требуемое распределение освещённости L(y), y eD, формируемое в выходной плоскости z = f, и требуемое распределение эйконала T(y), y e D, в этой же плоскости (рис. 1). Требуется найти такие функции u1 (x) и l (y), чтобы световой пучок, прошедший через оптический элемент, формировал в выходной плоскости z = f заданное распределение освещённости L(y) и заданный эйконал T(y).
a)
б)
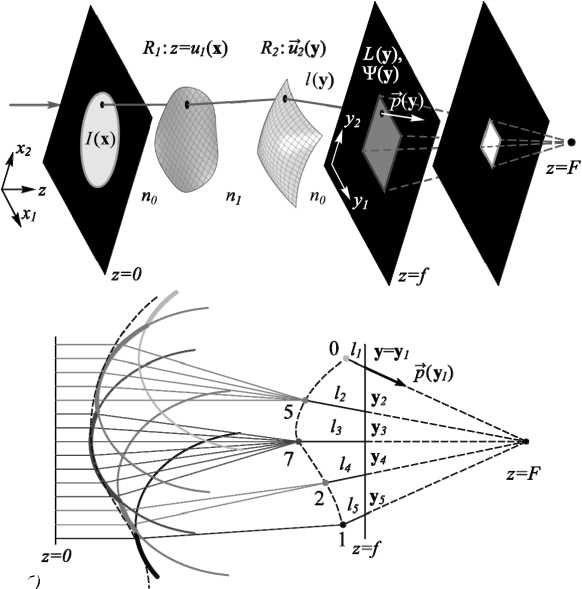
Рис. 1. (а) Геометрия задачи формирования пучка, обеспечивающего заданное распределение освещённости и заданный волновой фронт (функцию эйконала). Для примера показан случай формирования пучка со сходящимся сферическим фронтом. (б) Представление первой поверхнос ти (двумерного сечения) в виде сегментов линз, фокусирующих в точки второй поверхности. Сегменты линз показаны жирными линиями, пунктирной линией показана огибающая
2. Представление оптических поверхностей
Вторая поверхность R 2 оптического элемента определяется уравнением (2). Данное уравнение записано с учётом требуемой функции эйконала T ( y ) в плоскости z = f . Первая поверхность элемента R 1 может быть представлена в виде огибающей семейства поверхностей специального вида. Действительно, для дифференцируемых поверхностей R 1 , R 2 лучевое отображение у = у ( x ) можно описать следующим образом. Луч, исходящий из точки x e G , после преломления в точке ( x , u 1 ( x )) поверхности R 1 приходит в точку
M 2( y )= ( y , f ) - p ( y ) l ( y )
поверхности R 2 . Поэтому поверхность R 1 может быть представлена в виде огибающей семейства поверхностей, фокусирующих падающий пучок с плоским волновым фроном в точки поверхности R 2 (рис. 1 б ) [8].
Уравнение преломляющей поверхности (линзы) z = ulens (x), фокусирующей падающий пучок в точку u2(y) = (u2,ЛУ), u2,x2(y), u2,z (y) ) , несложно получить из условия равенства оптической длины пути лучей из точек плоскости z =0 до точки u2 (y) значению эйконала в данной точке
Т2 (y) = T(y) -nо l(y). Данное условие имеет вид n о u lens(x) +
+ П 1 Vil U 2 ( y ) - xl 12 + ( u 2, z ( y ) - U ens ( x ) ) 2 = ^ 2( y ),
где U2(y) = (u2,Ду),u2,x2(y)). Уравнение (5) определяет поверхность ulens (x; y) в неявном виде. Отметим, что координата y в (5) рассматривается как параметр, а декартовы координаты точки второй поверхности z/2(y) выражаются через функцию l (y) согласно (2). Чтобы подчеркнуть эти факты, далее мы будем записывать уравнение линзы в виде z = ulens(x; y, l (y)). Из (5) легко видеть, что получение явного выражения для ulens(x; y, l (y)) сводится к решению квадратного уравнения. Решая данное уравнение, получим ulens (x; У, l(y )) = g-1 ( П2u2z (y) - n0 V 2 (y ) ) -
2 2 (6)
-
- n 1 g - 1 V(V 2( y ) - n 0 u 2, z ( У ) ) - g ||u2( y ) - x|| ,
где g = n 2 - n 2 . Можно показать, что поверхность u lens ( x ; y , l ( y )) при n 0 < n 1 является эллипсодом вращения [19]. Ось эллипсоида параллельна оси z , а один из фокусов совпадает с точкой фокусировки i<2( y ). Таким образом, первая поверхность, описываемая функцией z 1 ( x ), является огибающей семейства эллипсоидов u lens ( x ; y , l ( y )) по параметрам y =(y 1 У 2 ) e D . Уравнение огибающей задаётся уравнением (6) и следующими двумя уравнениями [20]:
д ulens(x;y,l(y)) =0, i=1,2. (7)
д у ,
Отметим, что уравнения (7) при фиксированном значении x = (x1, x2) соответствуют критической точке функции ulens (x; y, l (y)) по переменным y1, y2. Далее мы будем рассматривать частный случай огибающей (6), (7), когда условие (7) соответствует не просто какой-то критической точке функции ulens(x; y, l (y)), а точке минимума (случай точки максимума рассматривается аналогично). В этом случае огибающая поверхность примет вид u-(x) min[ulens (x;y,l(y))]. (8)
Уравнение (8) позволяет определить лучевое отображение в виде
Y ( x ) = argmin [ u ^( x ; y , l ( y )) ] . (9)
y e D
Поскольку функция u lens ( x ; y , l ( y )) зависит от функции l ( y ), определяющей вторую поверхность, то уравнения (8), (9) позволяют сформулировать задачу формирования заданного распределения освещённости и волнового фронта как задачу расчёта такой функции l ( y ), что определяемое ею лучевое отображение (9) удовлетворяет закону сохранения светового потока, определённому уравнением (3) или (4).
-
3. Метод опорных квадрик
Метод опорных квадрик (МОК) [13–19] широко используется в задачах расчёта зеркал и преломляющих поверхностей, формирующих заданные распределения освещённости, и состоит в следующем. Требуемое непрерывное распределение освещённости приближается дискретным распределением, сосредоточенным в конечном числе точек. Оптическая поверхность представляется в виде кусочно-гладкой поверхности, состоящей из фрагментов квадрик. Далее параметры квадрик рассчитываются итерационно из условия получения требуемых значений светового потока в точках дискретного распределения.
В данном параграфе мы рассмотрим вариант МОК для решения задачи формирования заданного распределения освещённости и волнового фронта (рис. 1 а ). Вообще говоря, строгая формулировка МОК требует введения понятия т.н. слабого решения, позволяющего корректно определить решение задачи в случае, когда лучевое отображение имеет разрывы на множестве меры ноль [11, 15]. Однако для простоты изложения мы сконцентрируемся на практической стороне метода.
Пусть заданные непрерывное распределение освещённости L ( y ), y e D , и функция эйконала V ( y ), y e D , аппроксимируются дискретными распределениями L i = L ( y i ), i = 1, N и V i = V ( y i ), i = 1, N , заданными в N точках y i e D . В этом случае вектор-функция p ( y ), определяющая направления лучей, и функция l ( y ), задающая вторую поверхность, также заменяются наб орами ди скр етных значений p i = Р ( y i ), i = 1, N и l i ( y i ), i = 1, N . Значения l i далее будут варьироваться в процессе работы метода для достижения заданных значений о све щённости L i = L ( y i ) в точках u2i i = u 2( y i ), i = 1, N второй поверхности. При этом считается, что луч p i «перенесёт» световой поток L i = L ( y i ) со второй поверхности в точку y i выходной плоскости.
При введённых выше дискретных аппроксимациях поверхность R 1 будет представлять собой кусочногладкую поверхность, состоящую из фрагментов рефракционных линз (6) (эллипсоидов), фокусирующих падающий пучок с пл оск им волновым фронтом в точки u2i i = u 2( y i ), i = 1, N . Данная поверхность схематично изображена на рис. 1 б жирными сегментами линий, показывающих эллипсоиды, фокусирующие в отдельные точки второй поверхности.
Согласно формуле (8), функция u1 (x), задающая поверхность R1, имеет вид u1 (x) = min [ulens (x; y,-, li)]. (10)
Теперь для фиксированных значений l i , i =1, N , можно вычислить дискретное распределение энергии, формируемое в точках й2 , i при функции u 1 ( x ) (10). Согласно (9), (10), в точку u i 2 ( y i ) фокусируется световой поток из области C ( y i ; 1 1,..., l N ) с G , которая определяется следующим условием:
C ( y i ; l 1 ...., l N ) =
= { x e G | u lens ( x ; y i -, l ) < u ^( x ; y j , l y -), V j = 1, N } .
Соответственно, световой поток, фокусирующийся в точку й24 , можно вычислить как интеграл
L est, i = L est, i ( l 1 ...., I n ) = j I ( x )d x . (12)
-
C ( y i ; l 1 ,..., I n )
В практических расчётах для вычисления значений Lest,i используется метод трассировки лучей, схематично показанный на рис. 1б. В этом случае падающий пучок аппроксимируется набором из Ntr лучей, исходящих из узлов некоторой сетки xj, j=1,Ntr , в плоскости z = 0. Эти лучи «несут» значения светового потока Ij, j=1,Ntr , пропорциональные значениям освещённости, формируемой падающим пучком в узлах сетки. Согласно (10), для каждого луча, исходящего из точки xj, находится индекс линзы i (j) = arg min (u iens(Xj-; y„ l)), которую луч «встречает» первой (рис. 1б). Этот луч направляется в соответствующую точку йу второй поверхности. Далее в точках второй поверхности вычисляются световые потоки, равные световым потокам лучей, пришедших в эти точки. На рис. 1б расчётные значения светового потока схематично показаны цифрами, равными числу лучей, пришедших в точки второй поверхности.
В Приложении показано, что функция z = u lens ( x ; y , l ( y )) является монотонной по параметру 1 = 1 ( y ), причём d u lens/ d 1 <0. Это означает, что при увеличении значения l i (при условии сохранения остальных l j для j * i ) поверхность uiens ( x j ; y i , 1i ) «опускается». В этом случае область C ( y i ; l 1 ,..., l N ) увеличивается и соответственно увеличивается световой поток L est ,i = Lest , i ( 1 1 ,..., I N ). Поэтому если в точке й 2,j требуемый световой поток L d ( y i ) = L i > L est ,i , то требуется увеличить значение l i , и уменьшить в противном случае. Величину увеличения (уменьшения) l i естественно выбрать пропорциональной величине разности ( L i – L est ,i ) между заданным и расчётным значениями светового потока [19, 20]. Таким образом, значения l i можно рассчитывать ит ера ционно следующим образом. Обозначим 1 , , n , i = 1, N , значения 1 , , полученные на n -м шаге итерационного процесса. Тогда на шаге n +1 рассчитывает ся формируемое распределение L est ,i ( 1 1, n ,..., I n , n ), i = 1, N , и значения 1 , , n корректируются по правилу
-
1 , n + 1 = 1 , n + A n ■( L , - J I ( x )d x ) , i = 1,N , (13) I C ( y i ; 1 1, n ...., 1 N , n ) )
где A n > 0 - шаг алгоритма. Описанный выше метод является вариантом МОК. Предложенный метод не имеет строгого обоснования сходимости, однако в частном случае, когда волновой фронт выходного пучка является плоским (т.е при ^ ( y ) = Ф = const), МОК (13) можно рассматривать как метод градиентного спуска для максимизации вогнутой функции, являющейся дискретным аналогом функционала Лагранжа в задаче перемещения масс [20].
Интересно также отметить, что МОК (13) можно рассматривать как метод простой итерации решения системы нелинейных уравнений. Действительно, задачу расчёта значений 1i, i = 1, N, обеспечивающих требуемые значения светового потока L,, i = 1, N, можно рассматривать как решение следующей системы нелинейных уравнений
L i L est, i ( 1 1v, 1 N ) =
= L , — J I ( x )d x = 0, i = 1, N .
C ( y i ; 1 1 ,..., 1 n )
Систему уравнений (14) можно представить в следующем эквивалентном виде:
1i = 1i +A^( Li-Lest ,i( 11...., 1N )), i =1, N , (15)
4. Примеры расчёта4.1. Формирование квадратного пучка, обеспечивающего постоянную освещённость и обладающего сходящимся сферическим волновым фронтом
где A >0 - постоянный параметр. Сравнивая (13) и (15), легко видеть, что алгоритм (13) соответствует методу простой итерации для системы (14).
Вообще говоря, формулировка задачи в виде задачи решения системы нелинейных уравнений (14) или (15) позволяет предложить более эффективные алгоритмы, основанные, например, на квазиньютоновских методах. Однако, как показывают расчётные примеры, представленные в следующем параграфе, МОК в виде (13) уже позволяет эффективно решать задачу формирования световых пучков, обеспечивающих заданное распределение освещённости и заданный эйконал.
Для иллюстрации рабочих характеристик метода был рассчитан ряд оптических элементов, формирующих световые пучки, обеспечивающие заданные распределения освещённости и имеющие сферические волновые фронты (сходящиеся и расходящиеся). При расчете оптических элементов мы остановились на выходных пучках со сферическими волновыми фронтами, поскольку, по нашему мнению, такие пучки важны в прикладных задачах.
Был рассчитан оптический элемент, преобразующий пучок круглого сечения, имеющий плоский волновой фронт в плоскости z = 0 и формирующий в этой плоскости постоянное распределение освещённости
I ( x ) = 1/( n R 2 ), x e G = { ( x 1 , x 2)| x 2 + x 2 < R 2 } , (16)
в пучок квадратного сечения, формирующий постоянную освещённость и имеющий сферический волновой фронт. В этом случае требуемое распределение освещённости, формируемое в выходной плоскости z = f , имеет вид
L ( y ) = 1/ w 2, y e D =
= { ( У 1 , y 2 )| | У 1| < W /2,1 y 2, < w /2
где w – размер пучка (размер квадратной области D ). Будем считать, что фокус сферического волнового фронта выходного пучка расположен в точке x = (0,0, F ), где F >f Поскольку фокус расположен за выходной плоскостью, то формируемый пучок имеет сходящийся сферический фронт. Для указанного пучка функция эйконала в выходной плоскости будет иметь вид
Т ( y ) = ^ о + F - f - ^ у 2 + ( F - f ) 2 , (18) где ^ 0 - константа, задающая эйконал в точке у = 0 выходной плоскости. Данная константа равна оптической длине пути центрального луча, исходящего из точки x = 0 плоскости z = 0. Выбором значения ^ 0 обеспечивается требуемая толщина оптического элемента. Действительно, в силу симметрии задачи центральный луч должен распространяться по оси z без преломлений. Поэтому оптическая длина пути центрального луча в точке у = 0 равна n 1 1 0 + n0(f - 1 0)= ^ 0, где t 0 – толщина оптического элемента в точке x =0. Таким образом, толщина оптического элемента t 0 выражается через значение ^ 0 по формуле
1 0 = ( ^ 0 - n 0 f )/( n - n 0 ) . (19)
Расчёт элемента проводился при следующих параметрах: радиус падающего пучка R = 1 мм; размер формируемого квадратного пучка – w =2 мм; выходная плоскость – z = f = 10 мм; z -координата фокуса сферического волнового фронта выходного пучка F = 14 мм, значение эйконала в точке y =0 в выходной плоскости V 0=13 мм; показатель преломления материала элемента (область между двух рассчитанных поверхностей) – n 1 = 1,5; показатель преломления среды вне элемента – n 0 = 1.
МОК, описанный в предыдущем параграфе, допускает многомасштабную реализацию. Это означает, что расчет элемента можно проводить в несколько этапов на последовательно сгущающихся сетках (т.е. при п оследовательном увеличении числа точек y i , i =1, N , в дискретных аппроксимациях требуемых распределения освещённости и волнового фронта). При этом в качестве начального приближения для значений l i , задающих вторую поверхность элемента на более мелкой сетке на следующем этапе, можно использовать значения, полученные интерполяцией значений l i , рассчитанных на более грубой сетке на предыдущем шаге. Как показывают результаты расчетов, такой многомасштабный подход обеспечивает быструю сходимость итерационного процесса (13).
В настоящем примере расчёт поверхностей оптического элемента проводился в три этапа. На этапе 1 заданные распределение освещённости (17) и волновой фронт (18) были аппроксимированы дискретными распределениями, заданными на квадратной сетке, содержащей всего N = N1 =202 точек. При таком малом начальном числе точек метод (13) быстро сходится (за несколько сотен интераций). На этапе 2 заданные распределение освещённости и волновой фронт были аппроксимированы дискретными распределениями на сгущенной сетке из N = N2 = 1002 точек. В качестве начальных значений li, i=1,N2 , на сгущенной сетке использовались значения, полученные сплайновой интерполяцией значений li, i=1,N1 , рассчитанных на грубой сетке на этапе 1. При расчёте на сгущенной сетке было сделано 15000 итераций. Наконец, на этапе 3 использовалась сгущенная сетка из N = N3 = 2002 точек и, как и ранее, в качестве начальных значений li, i=1,N3 , использовались значения, полученные сплайновой интерполяцией значений li, рассчитанных на этапе 2. На этапе 3 также было сделано 15000 итераций. Общее время расчёта элемента на персональном компьютере (CPU Core i9-7940X) составило около 15 минут.
В соответствии с описанием МОК в предыдущем параграфе, на каждой итерации каждого этапа методом трассировки лучей осуществлялся расчет значений светового потока в точках u 2ii = ( y i , f ) - p Ji , i =1, N , и затем выполнялась коррекция значений l i по формуле (13). В методе трассировки лучей падающий пучок аппроксимировался набором из N tr =2 N лучей, заданных на квадратной сетке в плоскости z =0.
По окончании расчёта вто рая поверхность, заданная набором значений l i , i =1, N , была аппроксимирована по методу наименьших квадратов системой двумерных В-сплайнов [10, 20]. Далее по рассчитанной второй поверхности по формуле (8) была рассчитана первая поверхность. Рассчитанные поверхности оптического элемента приведены на рис. 2 а . На рис. 2 б - г показаны рассчитанные нормированные распределения освещённости, формируемые оптическим элементом в выходной плоскости z = f = 10 мм, в плоскости z = 11 мм и в плоскости z = 12 мм. Представленные результаты расчёта показывают формирование квадратного пучка. Нормированные СКО рассчитанных распределений освещённости от постоянного значения составляют 9,9% ( z = 10 мм), 8,6% ( z = 11 мм) и 10,1 % ( z = 12 мм). Линейное уменьшение размеров пучка, происходящее при увеличении расстояния от выходной плоскости, показывает, что волновой фронт сформированного пучка является сходящимся сферическим. Рассчитанное СКО оптической длины пути лучей в выходной плоскости от требуемой функции эйконала (18) составляет 14 нм.
-
4.2. Формирование квадратного пучка, обеспечивающего постоянное распределение освещённости и имеющего расходящийся сферический волновой фронт
-
4.3. Формирование пучка в виде квадратной рамки с расходящимся сферическим волновым фронтом
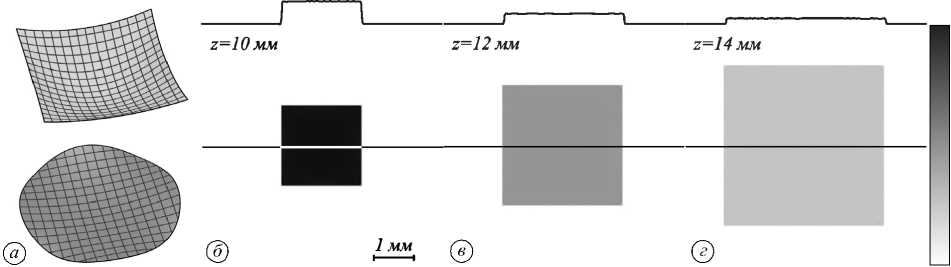
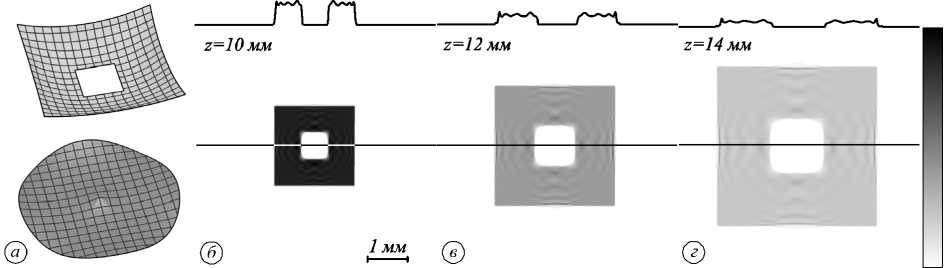
В качестве следующего примера был рассчитан оптический элемент, преобразующий падающий пучок с плоским волновым фронтом (16) в квадратный пучок, формирующий постоянное распределение освещённо- сти (17) с расходящимся сферическим волновым фронтом. В данном случае фокус сферического фронта выходного пучка расположен перед выходной плоскостью в точке X = (0,0, F), где F ¥(У) = ¥0 - f + F + VУ2+(f -F)2 , (20) где ¥0 - эйконал в точке у = 0 выходной плоскости. Расчёт элемента производился при F =6 мм и ¥0=11 мм. Все остальные геометрические и материальные параметры совпадают с параметрами предыдущего примера. Расчёт оптического элемента проводился в 3 этапа и полностью аналогичен расчёту элемента в примере 1. Рассчитанные поверхности оптического элемента приведены на рис. 3а. На рис. 3б-г показаны рассчитанные нормированные распределения освещённости, формируемые оптическим элементом в выходной плоскости z = f = 10 мм, в плоскости z = 12 мм и в плоскости z = 14 мм. Представленные результаты расчёта показывают формирование квадратного пучка. Линейное увеличение размеров пучка с ростом z подтверждает, что волновой фронт сформированного пучка является расходящимся сферическим. Рассчитанное СКО оптической длины пути лучей в выходной плоскости от требуемой функции эйконала (20) составляет 11 нм. Нормированные СКО рассчитанных распределений освещённости от постоянного значения составляют 6,3 %, 4,4% и 3,4% в плоскостях z = 10 мм, z = 12 мм и z = 14 мм соответственно. Отметим, что приведённые значения СКО меньше, по сравнению с СКО для элемента, рассчитанного в подпараграфе 4.1. Это связано с тем, что поверхности элемента, рассчитанного в настоящем подпараграфе, являются более гладкими и лучше представляются системой двумерных В-сплайнов. Рис. 2. Поверхности оптического элемента, преобразующего круглый пучок в квадратный пучок со сходящимся сферическим волновым фронтом (а); формируемые элементом распределения освещённости в различных плоскостях (б)-(г). Линиями сверху показаны сечения распределения освещённости В качестве более сложного примера был рассчитан оптический элемент, преобразующий пучок с плоским волновым фронтом (16) в пучок в виде квадратной рамки, имеющий расходящийся сферический волновой фронт. Данный пучок формирует постоянную освещённость в области в виде квадратной рамки L (y ) = 1/( w2 - w2), y £ D = SЛS2, (21) где Si = {(x 1,x2)||x 1|< Wi/2,|x2|< Wi/2|}, i =1,2 - квадраты со сторонами w1, w2 (w1 < w2). Функция эйконала в выходной плоскости z = f соответствует расходящемуся сферическому волновому фронту и имеет вид (20). Расчёт элемента производился при размерах выходного пучка w1 =2 мм и w2 = 1 мм. Все остальные параметры совпадают с параметрами предыдущего примера. Расчёт поверхностей элемента проводился в несколько этапов c последовательным сгущением расчётных сеток и аналогичен расчёту элементов в примерах 1, 2. Из-за того, что требуемое распределение имеет более сложный вид и задано в двухсвязной области, на последнем расчётном этапе использова- лась сетка из N = 3502 точек. При этом общее время расчёта элемента составило около 1 часа. Рассчитанные поверхности оптического элемента приведены на рис. 4а. Следует отметить, что в окрестности начала координат первая поверхность имеет изломы и по форме напоминает четырёхгранную пирамиду. Это связано с тем, что центральная часть первой поверхности отображает центральную часть падающего пучка (окрестность точки x =0) во внутренний контур квадратной рамки. Такое отображение является разрывным. Возможность применения МОК для расчёта кусочно-гладких поверхностей, реализующих разрывные лучевые отображения, является сильной стороной метода. В этом случае известные методы, основанные на численном решении НДУ эллиптического типа [3–9], становятся численно неустойчивыми. На рис. 4б-г показаны рассчитанные нормированные распределения освещённости, формируемые оптическим элементом в выходной плоскости z = f = 10 мм, в плоскости z = 12 мм и в плоскости z = 14 мм. Представленные результаты расчёта показывают формирование пучка в виде квадратной рамки. Нормированные СКО рассчитанных распределений освещённости от постоянного значения в области квадратной рамки составляют 8,3 % (z = 10 мм), 8,7 % (z = 12 мм) и 9,3 % (z = 14 мм). Линейное увеличение размеров пучка с ростом z подтверждает, что волновой фронт сформированного пучка является расхо- дящимся сферическим. Рассчитанное СКО оптической длины пути лучей в выходной плоскости от требуемой функции эйконала (20) составляет 17 нм. Рис. 3. Поверхности оптического элемента, преобразующего круглый пучок в квадратный пучок с расходящимся сферическим волновым фронтом (а); формируемые элементом распределения освещённости в различных плоскостях (б)-(г). Линиями сверху показаны сечения распределения освещённости Рис. 4. Поверхности оптического элемента, преобразующего круглый пучок в пучок в виде квадратной рамки с расходящимся сферическим волновым фронтом (а); формируемые элементом распределения освещённости в различных плоскостях (б)-(г). Линиями сверху показаны сечения распределения освещённости Заключение Предложен вариант метода опорных квадрик для расчёта преломляющих оптических элементов с двумя рабочими поверхностями, преобразующих падающий пучок с плоским волновым фронтом в выходной пучок, имеющий заданный волновой фронт и формирующий заданное распределение освещённости. С использованием метода рассчитаны оптические элементы, преобразующие круглый пучок с постоянной освещённостью в квадратные пучки со сферическими волновыми фронтами (сходящимися и расходящимися), а также в пучок в виде квадратной рамки с расходящимся сферическим волновым фронтом, заданный в двусвязной области. Приведённые примеры показывают хорошие рабочие характеристики метода. Последний пример формирования пучка в виде квадратной рамки демонстрирует возможность применения метода для расчёта оптических элементов с непрерывными кусочногладкими поверхностями. В силу обратимости хода лучей предложенный метод может быть также применён для расчёта оптических элементов, преобразующих пучок с произвольным волновым фронтом в выходной пучок с плоским волновым фронтом, формирующий заданное распределение осве- щённости. В частности, может быть решена практически важная задача формирования коллимированного оптического пучка с заданным распределением освещённости из точечного источника света. Работа выполнена при поддержке гранта РФФИ (проект № 18-29-03067) в части разработки метода расчета оптических элементов, а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части создания программных средств для моделирования работы рассчитанных элементов и в рамках выполнения работ лабораторией «Фотоника для умного дома и умного города» по Государственному заданию Самарского университета в рамках выполнения работ лабораторией «Фотоника для умного дома и умного города» по Государственному заданию Самарского университета (тема 19в-Р001-602) в части формулировки задачи максимизации вогнутой функции. Приложение 1 Докажем свойство монотонности функции ulens (x; y, l (y)) по параметру l = l (y). Дифференцируя уравнение (5) по параметру l, несложно получить производную дulens /дl в виде dUlens = - n 0 — n1 ( e^ ' x, У ), p fr) ) d l По - n (<,inc, <,reft ( X, У )) ’ где (a, b) обозначает скалярное произведение векторов, e._(x,y)=,; y -uM -(П2) 1'"*' ’’) |,<2(y)-Й1(х)||' единичный вектор луча после преломления в точке u1(x) = (x, u1(x)) первой поверхности, eVmc = (0,0,1) -единичный вектор направления лучей, падающих на первую поверхность. Обозначим adev,i (x,y), i =1,2, углы «девиации» на поверхностях элемента R1, R2. Под углом девиации мы понимаем угол между падающим на поверхность лучом и преломленным на этой поверхности лучом. В частности, скалярное произведение в знаменателе (П1) соответствует косинусу угла девиации на первой поверхности. Из закона преломления несложно получить, что косинусы углов «девиации» должны удовлетворять соотношению n о/ n < cos (adeV,i(x, y) )< 1, i = 1,2. (П3) Отметим, что не всякие распределения эйконала V (y) и освещённости L (y) могут быть созданы оптическим элементом. Это связано с ограниченными углами «девиации» лучей на поверхностях элемента. Например, если точка второй поверхности u2ii = t;2(yi) является «сильно» смещённой относительно оси, так что требуемый угол девиации лучей больше arcsin(n0/ n1), то не будет существовать линзы ulens (x; yi, li), фокусирующей в эту точку (выражение под корнем в (6) будет отрицательным). Будем считать, что функции V (y) и L (y) заданы корректно. В этом случае можно считать, что линзы, фокусирующие в точки г;2,i = u2(yi), i = 1, N, существуют и что косинусы углов между лучами, падающими на вторую поверхность, и заданными направлениями преломленных лучей p(y) удовлетворяют уравнению (П3). При указанных условиях скалярные произведения векторов падающих и преломленных лучей в (П1) удовлетворяют (П3) и поэтому производная dulens /дl является отрицательной.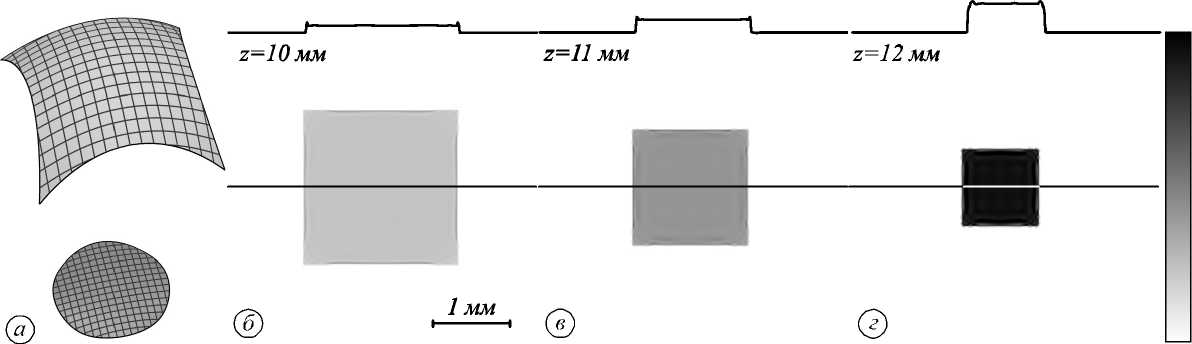
Список литературы Метод расчёта преломляющего оптического элемента, формирующего заданные распределения освещённости и волновой фронт
- Laser beam shaping: Theory and techniques / ed. By F.M. Dickey. S.C. Holswade. - New York: Marcel Dekker, 2000. - 427 p. - ISBN: 978-0-8247-0398-1.
- Laser beam shaping applications / ed. by F.M. Dickey. S.C. Holswade. D.L. Shealy. - Boca Raton: CRC Press. 2006. - 376 p. - ISBN: 978-0-8247-5941-4.
- Chang, S. Design beam shapers with double freeform surfaces to form a desired wavefront with prescribed illumination pattern by solving a Monge-Ampere type equation / S. Chang, R. Wu, L. An, Z. Zheng // Journal of Optics. - 2016. - Vol. 18, Issue 12. - 125602. - DOI: 10.1088/2040-8978/18/12/125602.
- Feng, Z. Creating unconventional geometric beams with large depth of field using double freeform-surface optics / Z. Feng, B.D. Froese, C.-Y. Huang, D. Ma, R. Liang // Applied Optics. - 2015. - Vol. 54, Issue 20. - P. 62776281. - DOI: 10.1364/A0.54.006277.
- Feng, Z. Simplified freeform optics design for complicated laser beam shaping / Z. Feng, B.D. Froese, R. Liang, D. Cheng, Y. Wang // Applied Optics. - 2017. - Vol. 56, Issue 33. - P. 9308-9314. - DOI: 10.1364/AO.56.009308.
- Bösel, C. Ray-mapping approach in double freeform surface design for collimated beam shaping beyond the paraxial approximation / C. Bösel, N.G. Worku, H. Gross // Applied Optics. - 2017. - Vol. 56, Issue 13. - P. 3679-3688. - DOI: 10.1364/AO.56.003679.
- Bösel, C. Double freeform illumination design for prescribed wavefronts and irradiances / C. Bösel, H. Gross // Journal of the Optical Society of America A. - 2018. - Vol. 35, Issue 2. - P. 236-243. - DOI: 10.1364/JOSAA.35.000236.
- Mao, X. Fast design method of smooth freeform lens with an arbitrary aperture for collimated beam shaping / X. Mao, J. Li, F. Wang, R. Gao, X. Li, Y. Xie // Applied Optics. -2019. - Vol. 58, Issue 10. - P. 2512-2521. - DOI: 10.1364/AO.58.002512.
- Wei, S. Double freeform surfaces design for beam shaping with non-planar wavefront using an integrable ray mapping method / S. Wei, Z. Zhu, Z. Fan, Y. Yan, D. Ma // Optics Express. - 2019. - Vol. 27, Issue 19. - P. 26757-26771. -DOI: 10.1364/OE.27.026757.
- Doskolovich, L.L. Designing double freeform surfaces for collimated beam shaping with optimal mass transportation and linear assignment problems / L.L. Doskolovich, D.A. Bykov, E.S. Andreev, E.A. Bezus, V. Oliker // Optics Express. - 2018. - Vol. 26, Issue 19.- P. 24602-24613. -DOI: 10.1364/OE.26.024602.
- Oliker, V. Beam shaping with a plano-freeform lens pair / V. Oliker, L.L. Doskolovich, D.A. Bykov // Optics Express. - 2018. - Vol. 26, Issue 15. - P. 19406-19419. - DOI: 10.1364/OE.26.019406.
- Rubinstein, J. Intensity control with a free-form lens / J. Rubinstein, G. Wolansky // Journal of the Optical Society of America A. - 2007. - Vol. 24, Issue 2. - P. 463-469. -DOI: 10.1364/JOSAA.24.000463.
- Caffarelli, L. On the numerical solution of the problem of reflector design with given far-field scattering data / L. Caffarelli, S. Kochengin, V. Oliker // Contemporary Mathematics. - 1999. - Vol. 226. - P. 13-32. - DOI: 10.1090/conm/226/03233.
- Kochengin, S. Computational algorithms for constructing reflectors / S. Kochengin, V. Oliker // Computing and Visualization in Science. - 2003. - Vol. 6. - P. 15-21. -DOI: 10.1007/s00791-003-0103-2.
- Oliker, V.I. Mathematical aspects of design of beam shaping surfaces in geometrical optics / V.I. Oliker. - In: Trends in nonlinear analysis / ed. by M. Kirkilionis, S. Krömker, R. Rannacher, F. Tomi. - Berlin, Heidelberg: Springer-Verlag, 2002. - P. 193-224. - DOI: 10.1007/978-3-662-05281-5_4.
- Fournier, F.R. Fast freeform reflector generation using source-target maps / F.R. Fournier, W.J. Cassarly, J.P. Rolland // Optics Express. - 2010. - Vol. 18, Issue 5. -P. 5295-5304. - DOI: 10.1364/OE.18.005295.
- Michaelis, D. Cartesian oval representation of freeform optics in illumination systems / D. Michaelis, P. Schreiber, A. Bräuer // Optics Letters. - 2011. - Vol. 36, Issue 6. -P. 918-920. - DOI: 10.1364/OL.36.000918.
- Oliker, V. Controlling light with freeform multifocal lens designed with supporting quadric method(SQM) / V. Oliker // Optics Express. - 2017. - Vol. 25, Issue 4. - P. A58-A72. - DOI: 10.1364/OE.25.000A58.
- Doskolovich, L.L. On the use of the supporting quadric method in the problem of the light field eikonal calculation / L.L. Doskolovich, M.A. Moiseev, E.A. Bezus, V. Oliker // Optics Express. - 2015. - Vol. 23, Issue 15. - P. 1960519617. - DOI: 10.1364/OE.23.019605.
- Mingazov, A.A. On the use of the supporting quadric method in the problem of designing double freeform surfaces for collimated beam shaping / A.A. Mingazov, D.A. Bykov, E.A. Bezus, L.L. Doskolovich // Optics Express. - 2020. - Vol. 28, Issue 15. - P. 22642-22657. -DOI: 10.1364/OE.398990.


