Метод расчёта течения газа в каналах газоструйных систем

Каналы различного вида, длины, формы, функционального назначения являются составной частью различных энергетических установок. Они

Уравнение энергии:

используются как в качестве основных, так и

д дт

f     w2

P S I C v T + у

д

+ — G c_vT + — + pSw = д x I v 2 I ^F

д x

вспомогательных элементов установок, в том числе в качестве протяжённых коллекторов со слия- нием и разделением потоков жидкости и газа.

В ряде энергетических установок протекают процессы с высокими скоростями и температурами рабочего тела, при этом происходит интенсивный теплообмен между газом и стенками канала. Такие процессы могут протекать в течение весьма малых промежутков времени. В силу существен- ного изменения давления, скорости и температуры по длине канала рабочие процессы не могут быть описаны в рамках модели несжимаемой жидкости. Целью данной работы является разработка эффективного метода решения краевой задачи с распределёнными параметрами.

Течение и теплообмен в таких коллекторах с достаточной для многих технических приложений точностью можно описать одномерными математическими моделями, включающими в себя уравнения неразрывности, количества движения и энергии, а также уравнение теплопроводности для стенок каналов [1]. Будем считать газ идеальным.

Уравнение неразрывности:

dp S д G _л

-t— + — = 0 дт    д x

Уравнение количества движения:

д G д f G ²   _OJ    _e G 2 П

— + — — + pS = 4— 7- . дт д x ^ S p     J      8 S ²p

= a(Tw -T)П.(3)

Уравнение теплопроводности стенки канала:

дTw = aw £f r 8Tw J .

дт r д r ( д r J

Уравнение состояния:

p =pRT .(5)

Начальные условия для уравнений (1)–(4) можно записать в следующем виде:

G (0, x ) = 0; p (0, x ) = po;(6)

T(0,x) = T; Tw (0,x) = T0.

В (1)-(6) G - массовый расход; p - плотность; S – площадь сечения; р – давление; П – периметр сечения канала; Т – температура; w – скорость; a - коэффициент теплоотдачи; ^ - коэффициент гидравлического сопротивления; т - время; х – продольная координата; r – радиальная координата; R – газовая постоянная; c_p , c_v – удельные теплоёмкости при постоянном давлении и объёме, соответственно; a – коэффициент температуропроводности; индексы: w – стенка канала; 0 – начальное значение.

Схема задачи с разделением потоков приведена на рис. 1. Газ, поступающий в канал, отводится к потребителям через отверстия в стенке канала. Расходы Gj , j = 1…J можно определить по известным соотношениям для истечения газа через отверстия [2].

На входе в канал при положительном значе- нии скорости задаются условия сохранения энер- гии и импульса:

/ RвхТвх (т) = k — 1

k P ( t ,0 ) + k - ¹ Р вх ( ^t )

+ p ( t ,0 ) G вх ( t ,0 )

² S вх ^р вх

P вх (^T) = P (^T ,° ) + p (^T ,0 ) w ² (^t ,0 ) .             ⁽⁸⁾

На конце канала граничное условие задаётся в виде

G ( t , l ) = G j ( t ) .

В (7)–(9) k – отношение теплоёмкостей c_p и c_v ; l – длина канала; индекс: вх – вход в канал.

Схема задачи со слиянием потоков приведена на рис. 2. Значения расходов G_j и температур T_j в источниках считаются известными функциями времени. В этом случае граничные условия задаются следующим образом:

pi (t)—p (т,0 Mi GiT^^;

• ²    S 1 ^р 1

T (t,0) = T (t) ;(11)

Pj (T, lJ )- Pвых (TMJ GJe(2T,lj ) .

• 2    S j P j

В (10)-(12) ^ - коэффициент гидравлического сопротивления; индекс 1 обозначает параметры первого источника.

Рассмотрим условия в точках разветвления потоков (рис. 3).

Для j -й точки разветвления можно записать следующие условия:

M (t,0) = Gi (t, lj — Gj;(13)

hM (t,0) = hi (t,li);(14)

Pi+1 (T,0) = Pi (T,li)-APj , где h - удельная энтальпия; APj - потери давления при переходе через j-ю точку отбора газа;

G ^j

G вх x=0                  x=l

x

Рис. 1. Схема канала с разделением потоков

G G G G —H G —H G 1-- M G j-1          j           j+1

Рис. 3. Расчётная схема разветвления потоков li – длина i-го участка канала между (j–1)-й и j-й точками разветвления.

В j -й точке слияния потоков (рис. 4) можно записать следующие условия:

M ( t ,0 ) = G ( t , l i ) + G j ;                  (16)

G ₊ 1 ( t , 0 ) h^ ( t ,0 ) = G i ( t , l i ) h i ( t , l i ) + G j h j ; (17)

P i + 1 (^{t ,0} ) = P i (^T , l i ) ^{— A} P j .                      ⁽¹⁸⁾

В (13)–(18) ноль означает начало i -го участка канала.

Для решения системы уравнений (1)–(3) применяется метод конечных разностей [3]. На участках канала между точками слияния или разветвления строится разностная сетка с количеством узлов N_i на каждом. Уравнения аппроксимируются неявными разностными схемами и приводятся к матричному двухточечному разностному уравнению вида [3]

A n Y_n m ^{+ 1} — B_n — 1 Y „™ + ¹ = C n , 1 <  n <  N i ,            (19)

где A n , B_{n —} 1 - матрицы размерности 3 x 3, Y_n , C_n -векторы размерности 3; Y = | G , p , T^ . Граничные условия (7), (8) или (10), (11) в разностной аппроксимации преобразуются к виду

A 1 Y 1 m ^{+ 1} = C 1 ,                                   (20)

где A 1 есть матрица размерности 2 x 3 , а C 1 - вектор размерности 2. Граничные условия (9) или (12) в разностной аппроксимации имеют следующий вид:

B n Y N ^{+ 1}' = C n ,                           (21)

где B_N есть матрица размерности 1 x 3, а C N -скаляр.

Условия сопряжения в точках разветвления и слияния (13)–(15) или (16)–(18) можно в разностной аппроксимации записать в виде

• Y N ^{+ 1} =a Y N + 1 ₊x i ,                     (22)

где a i - матрицы размерности 3 x 3 , а x i - вектор размерности 3.

Для решения задачи (19)–(21) с условиями сопряжения (22) применяется алгоритм ортогональной прогонки [4].

G j , T j

I I I I I r

G вых

> ---► x=0                  x=lx

Рис. 2. Схема канала со слиянием потоков

Gm	ki re Gi	\Gj e G/l1 ri	Gju - Gi+i
h	j- 1	jj	+ 1

Рис. 4. Расчётная схема слияния потоков

Теплоэнергетика

1,2

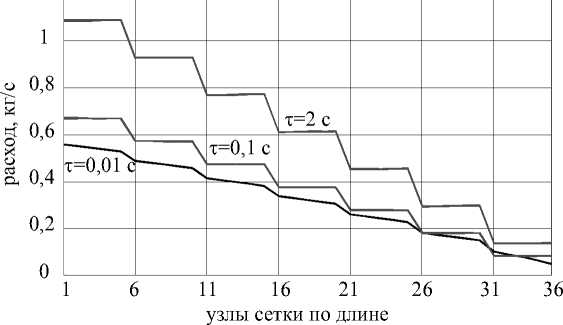
Рис. 5. Изменение расхода по длине канала с разделением потоков

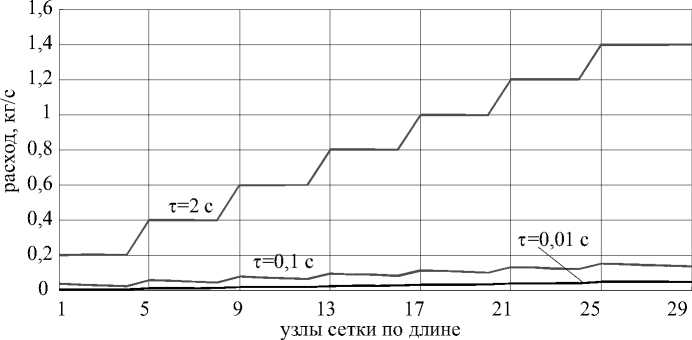
Рис. 6. Изменение расхода по длине канала со слиянием потоков

Уравнение теплопроводности (4) с граничными условиями третьего рода аппроксимируется неявной разностной схемой и решается методом трёхточечной скалярной прогонки по толщине стенки в каждом из узлов сетки по длине канала [4].

На рис. 5 и 6 показано изменение расхода газа по длине каналов с разделением и слиянием потоков в различные моменты времени.

Выводы

• 1.    Разработанный метод решения краевой задачи обладает высокой вычислительной эффективностью и позволяет анализировать высокоинтенсивные режимы работы канала при наличии источников и (или) стоков массы как c теплообменом со стенками канала, так и без него.

• 2.    Данный метод можно применять как для течения сжимаемого газа, так и несжимаемой

жидкости при условии применения соответствующего уравнения состояния.