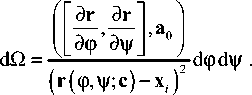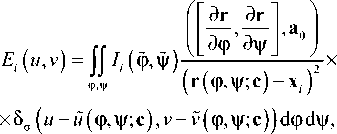Метод расчёта зеркал для формирования заданных двумерных распределений освещённости
Автор: Бызов Егор Владимирович, Моисеев Михаил Александрович, Досколович Леонид Леонидович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 1 т.36, 2012 года.
Бесплатный доступ
Представлен метод расчёта отражающей поверхности, формирующей заданное двумерное распределение освещённости при протяжённом источнике. Метод основан на представлении отражающей поверхности в виде бикубического сплайна и последующей оптимизации её параметров из условия формирования заданного светового распределения. Рассчитаны две отражающих поверхности, формирующие равномерно освещённые прямоугольную и эллиптическую области. Неравномерность распределения освещённости в обоих случаях составила менее 10 %.
Отражающая поверхность, зеркало, распределение освещённости, обратная задача, трассировка лучей
Короткий адрес: https://sciup.org/14059051
IDR: 14059051 | УДК: 535
Method for design of reflective surfaces producing prescribed two-dimensional irradiance distributions
A method for design of reflective surface producing the prescribed irradiance distribution from extended light source is presented. The method includes parameterization of the reflective surface by bicubic spline and optimization of its parameters from condition of required irradiance distribution generation. The surfaces producing uniformly illuminated rectangular and elliptical areas are computed. The non-uniformity of the generated irradiance distribution is less than 10% in both cases.
Текст научной статьи Метод расчёта зеркал для формирования заданных двумерных распределений освещённости
В общем случае излучающий элемент светодиода излучает свет во всех направлениях в телесном угле, соответствующем полусфере. Применение светодиодов в системах освещения требует использования вторичной оптики, направляющей излучаемый световой поток в заданную область пространства и обеспечивающей формирование в этой области заданного распределения освещённости. В качестве вторичной оптики используются оптические элементы с преломляющими или отражающими поверхностями, устанавливаемые непосредственно над излучающим элементом. Задача расчёта отражающей (преломляющей) поверхности из условия формирования заданного распределения освещённости является задачей высокой сложности и даже в приближении точечного источника сводится к решению нелинейного дифференциального уравнения второго порядка в частных производных эллиптического типа [1-4]. Аналитические решения данного уравнения возможны только в тривиальных случаях, соответствующих задачам с радиальной и цилиндрической симметрией [5-8]. В настоящее время для расчёта отражающих (преломляющих) поверхностей свободной формы используются различные численные и итерационные методы [9-16]. Эффективность существующих методов является недостаточно высокой, и задача расчёта зеркала для формирования постоянной освещённости в прямоугольной области по-прежнему имеет большое практическое значение [14]. В работах [17,18] авторами статьи предложен эффективный итерационный метод расчёта преломляющих поверхностей для формирования заданных распределений освещённости. Метод основан на представлении преломляющей поверхности в виде бикубического сплайна, заданного в сферической системе координат, и последующей оптимизации его параметров. В настоящей работе рассмотрена модификация этого метода для случая расчёта отражающих (зеркальных) поверхностей. Примеры расчёта зеркал для формирования постоянной освещённости в областях прямоугольной и эллиптиче ской формы демонстрируют высокие рабочие характеристики метода.
1. Постановка задачи
Пусть источник света (светодиод) расположен в начале координат и излучает в полусферу z < 0 . В полупространстве z < О находится зеркальная поверхность г, отражающая лучи от источника (рис. 1). Задача заключается в определении формы зеркала г из условия формирования в выходной плоскости z = f, f > 0 заданного распределения освещённости ^(щг) , где u,v - декартовы координаты при z = f.
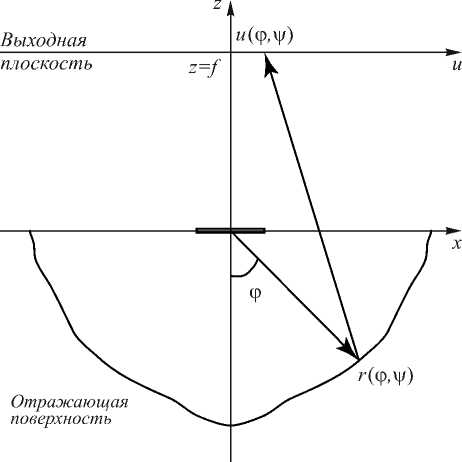
Рис. 1. Взаимное расположение источника, зеркала и выходной плоскости
Представим поверхность зеркала г через модуль её радиус-вектора г((р,у), где фе[0,2л), \|ге [0, л/2] - углы сферической системы координат, причём \|/ - угол между радиус-вектором и вектором (0,0,-1). Следуя [16-18], определим функцию модуля радиус-вектора в виде бикубического сплайна г(ф,ф;с) с вектором параметров с. Вектор с содержит значения модуля радиус-вектора, а также его первые и смешанную производные в узлах сетки (ф,,фу) > соответствующей некоторому разбиению прямоугольника (ф,ф) е [0,2л)х[0,л/2]. Задачу расчёта отражающей поверхности сформулируем как задачу минимизации следующей функции невязки [18]:
е(с) = ||Е(м,у;с)-£0(и,у)|| =
= (^о (“’V)-^(M’v’c))2 dwdv —> min, где S - площадь области S , в которой требуется сформировать заданное распределение освещённости £0(и,у), а Е(и,у;с) - распределение освещённости, формируемое отражающей поверхностью с вектором параметров с.
Количество параметров оптимизации в задаче оптимизации (1) равно количеству узлов сплайновой сетки, умноженному на четыре (в каждом узле необходимо определить значение модуля радиус-вектора и трёх его производных). При формировании симметричных распределений освещённости, соответствующих прямоугольной или эллиптической области, функцию г(ф,ф) достаточно определить в первом квадранте. Это позволяет уменьшить число параметров оптимизации в четыре раза.
-
2. Расчёт формируемого распределения освещённости при точечном источнике излучения
Для решения задачи оптимизации (1) необходимо разработать метод решения прямой задачи расчёта распределения освещённости Е^и, v;c) [17], формируемого зеркальной поверхностью с вектором параметров с. Рассмотрим решение данной задачи для случая точечного источника, расположенного в начале координат.
Определим соответствие между угловыми координатами луча, выходящего из источника, и координатами точки прихода отражённого от зеркала луча в выходную плоскость z = / . Введём единичный вектор а0(ф,ф), задающий направление падающего на зеркало луча:
ао Ф>¥ ------7-(2)
г(ф,ф;с)
Согласно закону Снеллиуса, единичный вектор отражённого луча а](ф,ф) имеет вид:
-
а, (ф, ф) = а0 (ф, ф) - 2 (а0, п) ■ п(ф, ф),(3)
где z , Гдг dr 1 /ГЭг dr 1
п(”
-
- единичный вектор нормали к поверхности зеркала. Квадратные скобки в (4) обозначают векторное произведение. Так как точка г(ф,ф) является началом отражённого луча, а вектор а, (ф,ф) определяет его направление, то несложно получить координаты точки пересечения отражённого луча с выходной плоскостью в виде:
й(ф,ф;с) = г(ф,ф;с)8тфсо8ф +
+ а1х(ф,ф;с)/(ф,ф;с),
г(ф,ф;с) = г(ф,ф;с)8тфзтф +
+ а,Дф,ф;с)/(ф,ф;с), где 7(ф,ф;с) = (/ + г(ф,ф;с)со8ф)/а,Дф,ф;с) -расстояние, пройденное отражённым лучом до выходной плоскости z = / . Отметим, что выражения (5) не учитывают возможность двойного отражения луча от зеркальной поверхности. Такое допущение широко используется при расчёте зеркал [5,6] и не является существенным ограничением.
Получим интегральное выражение для распределения освещённости £(м,г), формируемого в выходной плоскости отражающей поверхностью с вектором параметров с. Согласно закону сохранения светового потока, световой поток, излученный источником в элемент телесного угла dQ = зтфйфйф, равен световому потоку, попавшему на соответствующий элемент площади dudv в выходной плоскости:
7(ф,ф)8тфйфйф = £(w,v;c)dwdv. (6)
Используя свойства двумерной дельта-функции Дирака, преобразуем выражение (6) к интегральному виду:
ZT(m,v;c)== /(ф,ф)$тфх
х§(и-й(ф,ф;с),г-г(ф,ф;с))йфйф.
Для численных расчётов дельта-функцию в (7) следует аппроксимировать функцией Гаусса:
E(m,v;c) = Jf 7(ф,ф)$тфХ v-v (8)
хЗДи-й(ф,ф;с),у-у(ф,ф;с))йфйф, где
5а(и-м(ф,ф),г-у(ф,ф))=-^-ехр^-“ ^/
Выражение (8) представляет собой усреднённое распределение освещённости в выходной плоскости, причём радиус усреднения определяется параметром о функции Гаусса.
3. Расчёт формируемого распределения освещённости при протяжённом источнике излучения
Рассмотрим случай протяжённого источника излучения, расположенного в области
G
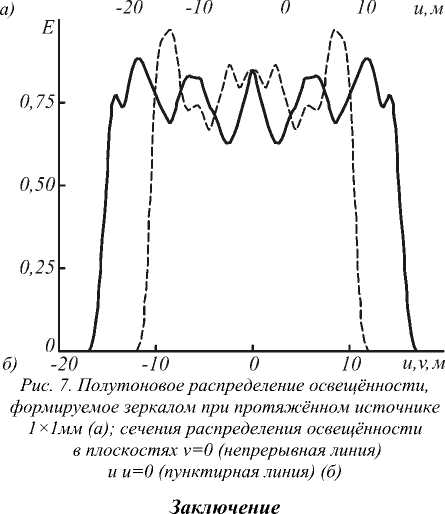
в плоскости - = 0 . Аппроксимируем протяжённый источник набором
N
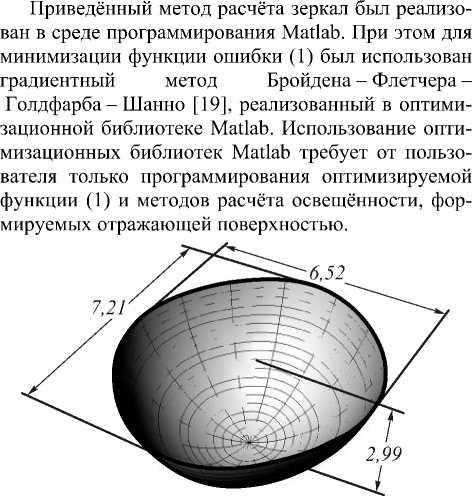
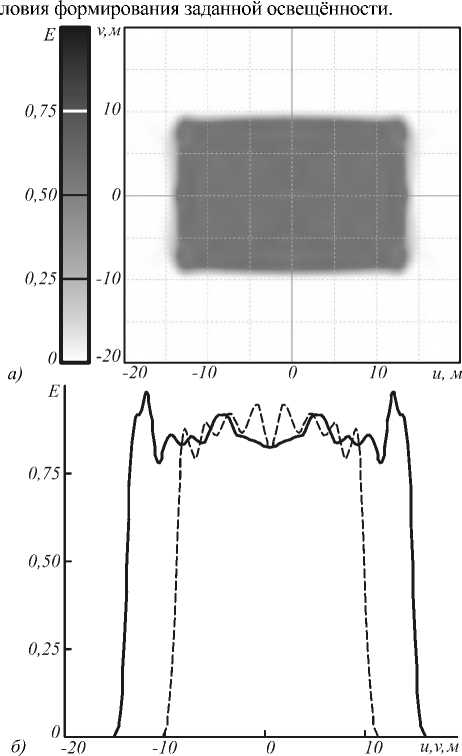
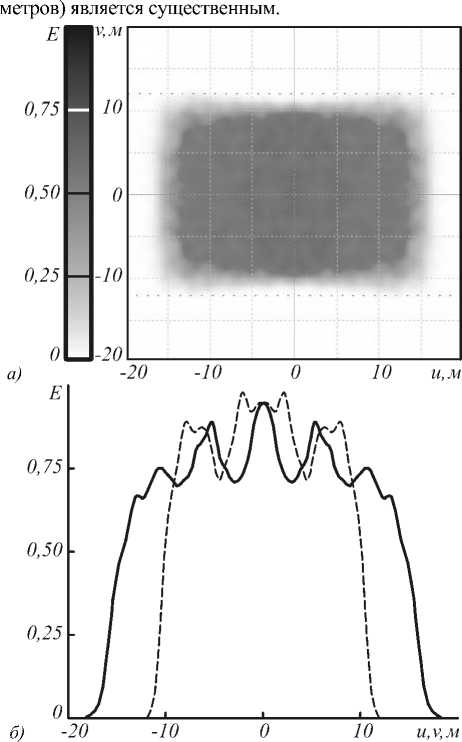
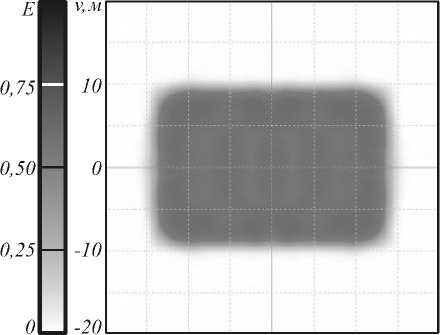
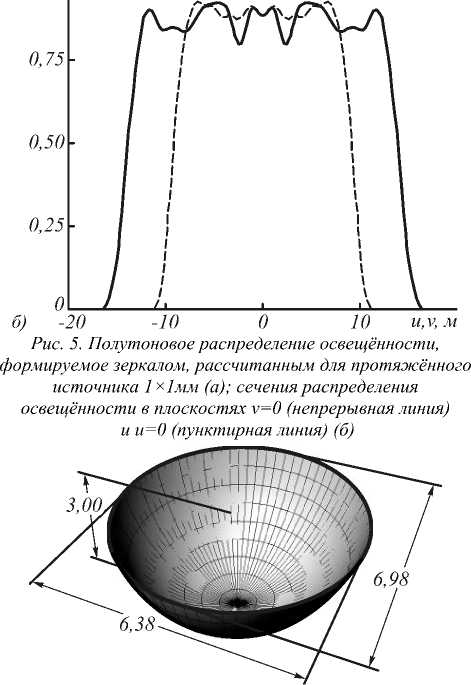
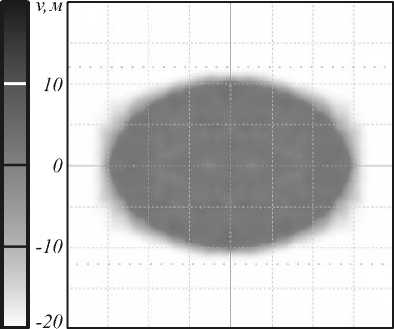
точечных источников с распределениями интенсивности /z( ie 1,...,А и представим распределение освещённости от протяжённого источника в виде суммы распределений освещённости Е; (t/,v;c), формируемых точечными источниками: Е х8„(1/-м(ф,\|/;с),у- )) бф бф х При А —э оо сумма (13) переходит в интеграл по поверхности G протяжённого источника: Е^и, г) = || || 5(ф,ф,х;с)а0. G<р,у dr dr dф ’ dф (г-х)1 :—-х £(m,v;c) = У Е( (u,v;c) . (9) i=i X§„ (z/ — u(ф,"ф;c), v- v((p,\p;c))d поверхности. Получим интегральное выражение для распределения освещённости, формируемого точечным источником с функцией интенсивности /Дер,у) и расположенным в точке xz = (x^ v, , 0). Элементар ный телесный угол с вершиной в точке х,, соответ ствующий элементу площади отражающей поверх ности dS = dr dr Эф ’ d\|/ ДфД\|/, имеет вид: (Ю) Подставив (10) в (8), вместо sin\|/d(pd\p получим (И) 4. Примеры расчёта отражающих поверхностей Рис. 2. Зеркало, формирующее равномерное распределение освещённости в прямоугольной области 26,6*17,7 мм на расстоянии 10 мм при точечном ламбертовском источнике (габаритные размеры указаны в миллиметрах) где ф = arctan /Д<рд|Лс)-у, г (ф,\|/;с)-л; ’ ф = arccos -г(ф,ф;с) |г(ф,у;с)-х,| Отметим, что для расчёта функций 77 (ф. ф) и г-(ф,\|т) в (И) необходимо использовать выражение (2) при a0( v) = г(ф.у;с)-х, |г (ф,ф;с) — хг| Таким образом, выражение для суммарного усреднённого распределения освещённости E^u,v^, фор мируемого N точечными источниками, имеет вид: Рассмотрим два примера, иллюстрирующих работу метода. На рис. 2 приведена рассчитанная с помощью выражений (1), (8) поверхность зеркала, формирующего постоянное распределение освещённости в прямоугольной области 26,6x17,7 мм на расстоянии 10 мм при точечном ламбертовском источнике излучения. В качестве начального приближения для зеркальной поверхности была использована осесимметричная поверхность, формирующая постоянное распределение освещённости в круге с радиусом 12,2 мм и рассчитанная аналитическим методом [5,6]. Для оптимизации осесимметричная поверхность была аппроксимирована (в первом квадранте) бикубическим сплайном с 56 параметрами. Распределение освещённости, формируемое рассчитанной поверхностью, приведено на рис. 3 и показывает формирование равномерно освещённой прямоугольной области заданного размера. Среднеквадратичное отклонение (СКО) формируемого распределения освещённости от равномерного составило 7,5%. Все распределения освещённости, представленные в статье, получены с помощью коммерческого программного обеспечения по моделированию светотехнических систем ТгасеРго8 [20]. Это подтверждает правильность выполненных расчётов. Отметим, что программа ТгасеРго8 предназначена только для моде лирования и не позволяет рассчитывать зеркала из ус- Рис. 3. Полутоновое распределение освещённости, формируемое зеркалом на рис. 2 при точечном источнике (а); сечения распределения освещённости в плоскостях v=0 (непрерывная линия) и и=0 (пунктирная линия) (б) На рис. 4 приведено распределение освещённости, формируемое зеркальной поверхностью на рис. 2 при протяжённом источнике излучения с размерами 1x1 мм. Такие размеры источника соответствуют размерам излучающем площадки светодиода Luxeon Rebel. Отметим, что расстояние от источника до вершины зеркала на рис. 2 составляет всего 2,99 мм, то есть всего в три раза больше стороны источника. Рис. 4 показывает существенное ухудшение равномерности формируемого распределения по сравнению с рис. 3, СКО распределения освещённости на рис. 3 от равно мерного распределения составляет 21%. Таким обра зом, учёт размеров источника излучения при расчёте компактных зеркал (с размерами в несколько милли- Рис. 4. Полутоновое распределение освещённости, формируемое зеркалом на рис. 2 при протяжённом источнике Iх! мм (а); сечения распределения освещённости в плоскостях v=0 (непрерывная линия) и и=() (пунктирная линия) (б) Зеркальная поверхность на рис. 2 была дополнительно прооптимизирована с использованием выражений (1), (13) для протяжённого ламбертовского источника с размером 1x1 мм. Внешний вид зеркальной поверхности изменился несущественно (максимальные изменения модуля радиус-вектора поверхности не превысили 0,1 мм). Распределение освещённости, формируемое зеркалом, рассчитанным для протяжённого источника, приведено на рис. 5 и показывает формирование значительно более равномерного прямоугольника. Среднеквадратичное отклонение распределения на рис. 5 от постоянного составляет 9,6 %. В качестве второго примера была рассчитана поверхность зеркала (рис. 6) для формирования равномерного распределения освещённости в эллиптической области с полуосями 15 мм и 10 мм на расстоянии 10 мм от протяжённого ламбертовского источника 1x1 мм. В качестве начального приближения также использовалась осесимметричная поверхность, формирующая постоянную освещённость в круге. а) -20 -10 0 10 и,м Е Рис. 6. Зеркало, формирующее равномерное распределение освещённости в эллиптической области с полуосями 15 мм и 10 мм на расстоянии 10 мм при ламбертовском источнике 1*1 мм (габаритные размеры указаны в миллиметрах) Для оптимизации поверхность в первом квадранте была аппроксимирована бикубическим сплайном с 56 параметрами. Оптимизация, как и ранее, проводилась в два этапа: сначала была рассчитана поверхность, формирующая заданное распределение освещённости при точечном источнике, затем была проведена дополнительная оптимизация поверхности с учётом размеров источника излучения. Распределение освещённости, формируемое рассчитанной поверхностью (рис. 6), приведено на рис. 7 и показывает формирование равномерно освещённой области эллиптической формы с заданными размерами. СКО формируемого распределения освещённости 0,75 0,50 0,25 от равномерного распределения составляет 8,8 %. Е О В работе представлен метод расчёта зеркальной поверхности свободной формы из условия формирования заданного распределения освещённости. Метод учитывает размеры источника излучения, что позволяет его использовать при расчёте компактных зеркал с размерами всего в несколько раз превышающими размеры источника излучения. Рассчитаны поверхности зеркал с толщиной 3 мм, формирующих равномерные распределения освещённости в прямоугольной (26,6* 17,7 мм) и эллиптической (полуоси 15 мм и 10 мм) областях при протяжённом ламбертовском источнике 1 х 1 мм. СКО формируемых зеркалами распределений освещённости от равномерных распределений составило менее 10 %, что свидетельствует о хорошей работоспособности разработанного метода. Работа выполнена при поддержке государственных контрактов 07.514.11.4055, 07.514.11.4060 и 07.514.11.4105, гранта Президента Российской Федерации НШ-4128.2012.9 и грантов РФФИ №№ 1007-00553 и 11-07-13164.
